齿轮传动是机械系统中应用最广泛的运动和动力传递形式, 对系统的动态特性有很大影响[1]。如今, 大功率、高转速是齿轮传动的主流发展趋势, 在这种严苛的工况环境下, 振动和噪声必定会对系统造成很大影响。时变啮合刚度作为齿轮传动系统的一种主要内激励, 其是振动和噪声的主要源头, 能够准确和快速地计算时变啮合刚度, 这是齿轮系统动力学分析的重要基础。
对于齿轮时变啮合刚度的计算, 国内外已经进行了很多研究, 主要的计算方法包括材料力学法、弹性力学法、石川公式法和有限元法。文献[2]将有限元法与弹性接触理论相结合进行齿轮啮合刚度计算。文献[3]基于势能法提出了一种考虑齿根圆与基圆不重合时的斜齿轮时变啮合刚度修正计算方法。文献[4]基于切片法建立了一种考虑修形的变齿厚齿轮时变啮合刚度求解模型, 并对传统Weber法进行了改进。文献[5]对比分析了直齿轮不同接触模型的啮合刚度。文献[6]提出了一种考虑非线性接触刚度和齿廓修形的一种啮合刚度计算改进模型。文献[7]针对裂纹直齿圆柱齿轮时变啮合刚度的计算提出了一种改进的分析模型。文献[8]根据力、变形分解原理和刚度、误差耦合关系, 提出了一种考虑轴向变形以及齿廓修缘的斜齿轮啮合刚度解析计算模型。文献[9]提出基于轮齿承载接触分析、考虑齿轮轴扭转变形的轮齿啮合刚度计算方法。文献[10]基于Weber能量法推导了直齿轮时变啮合刚度的数值积分公式, 并采用变增量、无限逼近的方法对齿轮啮合点进行确定。文献[11]将轮齿简化为悬臂梁, 采用势能法计算了考虑齿轮基体变形的齿轮时变啮合刚度。文献[12]综合考虑基圆与齿根圆不重合因素及裂纹区的变形能, 提出了一种含裂纹故障斜齿轮副时变啮合刚度的改进算法。文献[13-15]中建立了有限元模型, 使用有限元法计算了齿轮的时变啮合刚度。文献[16]建立了基于加载轮齿接触分析的稳健模型来计算直齿轮和斜齿轮的啮合刚度。文献[17] 提出了一种改进的含有齿廓修形的直齿轮时变啮合刚度解析算法。文献[18]提出了一种含有齿根裂纹的直齿轮时变啮合刚度计算模型, 可以计算含有不同尺寸裂纹轮齿的时变啮合刚度。文献[19]建立提出了一种改进的齿尖剥落模型, 推导了轮齿含有齿尖剥落时的时变啮合刚度的解析方程。文献[20]基于齿面LTCA方法计算人字齿轮时变啮合刚度, 并以啮合刚度波动幅值为目标, 对人字齿轮进行了齿面修形优化。文献[21]基于势能法和数值积分公式, 提出了涉及齿廓修形参数和退刀槽宽度的人字齿轮啮合刚度精确计算方法。文献[23]重点研究了考虑轴向啮合力的斜齿轮副时变啮合刚度计算方法。文献[24]建立了轴向轮齿刚度和轴向基体刚度的斜齿轮副时变啮合刚度模型, 并研究了摩擦力对啮合刚度的影响。
尽管许多学者已经对齿轮的啮合刚度进行了大量研究, 但是目前在对人字齿轮啮合刚度进行计算时大多忽略了轴向力的影响, 导致计算结果不够准确, 另外对于含修形, 尤其是齿向修形的人字齿轮啮合刚度的计算研究也较少, 因此, 本文结合切片法与势能法, 提出了一种考虑轴向力和修形的人字齿轮副时变啮合刚度的解析算法, 并将计算结果与有限元和ISO标准计算结果进行比较, 验证该算法的准确性, 最后分析了齿廓修形量、齿廓修形长度及齿向修形量对人字齿轮副啮合刚度的影响。
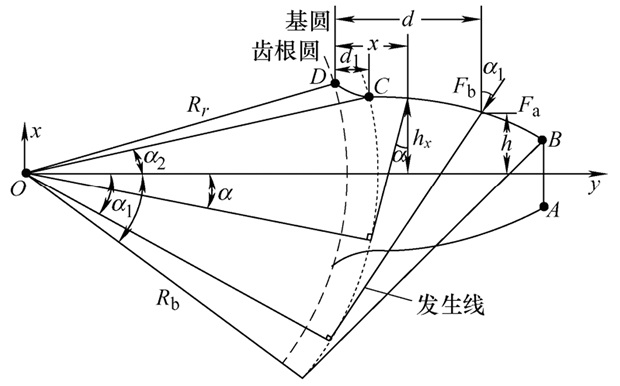
1 含修形的人字齿轮副时变啮合刚度算法 1.1 考虑轴向力的轮齿刚度计算直齿轮的单个轮齿可以直接简化为变截面悬臂梁, 载荷作用于齿面发生弹性变形。图 1为直齿轮单个轮齿的悬臂梁模型。
|
| 图 1 直齿轮单个轮齿悬臂梁模型 |
根据材料力学与弹性力学相关知识可知, 轮齿变形导致轮齿内产生剪切势能Us、弯曲势能Ub、轴向压缩势能Ua以及齿轮赫兹势能Uh, 根据势能与刚度关系可以求解刚度。轮齿变形后的势能可表示为[3]
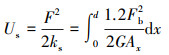
|
(1) |
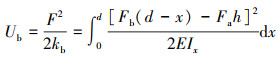
|
(2) |
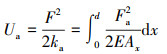
|
(3) |
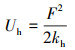
|
(4) |
式中: F为啮合力; Fa为径向力; Fb为圆周力; ks为剪切刚度; kb为弯曲刚度; ka为径向压缩刚度; kh为赫兹接触刚度; G为剪切模量; E为弹性模量; d为齿根到接触点的距离; h为接触点与轮齿中心线的距离; x为基圆到啮合点之间任意一点到基圆的距离。
对于人字齿轮而言, 其由左右两侧斜齿轮和退刀槽构成[21]。不考虑退刀槽的刚度, 人字齿轮两侧的斜齿轮由于螺旋角大小相同, 旋向相反, 使得两侧的斜齿轮处于相同的啮合状态, 因此, 人字齿轮的时变啮合刚度可以简化为2个斜齿轮的时变啮合刚度的并联。
从人字齿轮的结构特点分析, 假设两侧斜齿轮之间的退刀槽为刚性, 且两侧完全对称, 要求解人字齿轮副的时变啮合刚度, 首先需求解一侧斜齿轮副的时变啮合刚度。斜齿轮由于螺旋角的存在, 并不能像直齿轮一样将单个轮齿直接简化为悬臂梁, 而应该由二维平面问题变成三维空间问题。
利用切片的思想[4], 将人齿轮中每一侧斜齿轮的轮齿沿着齿宽方向分割成很多薄片, 斜齿轮被离散成依次旋转一个角度的N片直齿轮的组合。对于具有较大重合度的斜齿轮, 其沿着接触线的载荷不会出现较大的变化, 因此假设相邻的齿轮薄片上的载荷相等, 且薄片与薄片之间不考虑耦合的影响。经过切片离散之后, 每一片均可以看作一个直齿轮, 对其建立悬臂梁模型求其刚度, 再将薄片的刚度叠加起来就可以得到单个轮齿的啮合刚度。
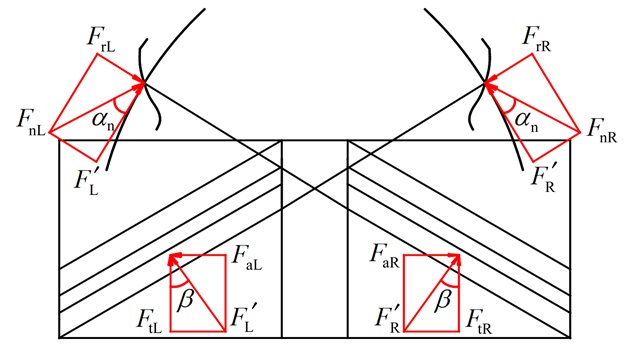
尽管人字齿轮的轴向力相互抵消, 但是两侧轴向力抵消后, 只是避免人字齿轮发生轴向窜动, 而轴向力依然作用于两侧斜齿轮的轮齿上, 如图 2所示, 左侧斜齿轮的轴向力FaL和右侧斜齿轮的轴向力FaR分别作用在两侧的轮齿上。如果不考虑轴向力的影响, 就会导致计算后人字齿轮副时变啮合刚度与实际存在偏差。
|
| 图 2 人字齿轮传动的作用力 |
计算人字齿轮副时变啮合刚度时, 对一侧斜齿轮时变啮合刚度的求解是基础, 下文中以人字齿轮一侧的斜齿轮作为对象进行求解。由于斜齿轮螺旋角的存在, 斜齿轮在分度圆上的3个分力为
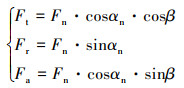
|
(5) |
式中:Ft为圆周力;Fr为径向力;Fa为轴向力;Fn为名义法向力;αn为法向压力角;β为分度圆螺旋角。
(5) 式为分度圆处啮合时的名义法向力、轴向力、径向力和圆周力的计算公式, 然而各力随着压力角和螺旋角的改变而改变, 因此要求任意啮合点处的名义法向力、轴向力、径向力和圆周力, 就要对任意啮合点处的压力角和螺旋角进行计算, 任意啮合点处的端面压力角为αti=arccos(rb/ri), 任意啮合点处的螺旋角为βi=arctan(ritanβ/r), 代入(5)式中可以得到任意啮合点处的圆周力、径向力和轴向力, 表达式为

|
(6) |
将(6)式代入(1)~(3)式中, 然后进行简化, 可以消除Fni, 得到与名义啮合力无关的刚度计算公式, 假设一个沿着齿宽方向N等分的轮齿, 某一时刻有m片接触(其中m≤N), 则此时单个轮齿的剪切刚度ks、弯曲刚度kb、轴向压缩刚度ka, 可表示为
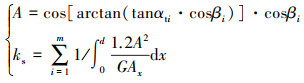
|
(7) |
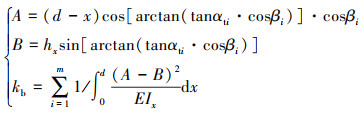
|
(8) |
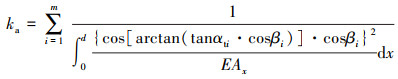
|
(9) |
式中:αti为端面齿廓上第i片轮齿啮合点处的压力角;βi为第i片轮齿啮合点处的螺旋角;hx为接触点x到轮齿中心线的距离。
由于(7)~(9)式中仅考虑到了圆周力和径向力, 而忽略了轴向力的影响, 为了更加真实地反映斜齿轮的刚度, 还应该考虑斜齿轮的轴向力所引起的轮齿的弯曲势能、剪切势能和轴向压缩势能。由于切片法切分后, 每一片轮齿的厚度非常小, 压缩势能可以忽略, 因此, 根据轴向力所引起的轮齿的弯曲势能、剪切势能计算轴向弯曲刚度和剪切刚度, 其表达式为
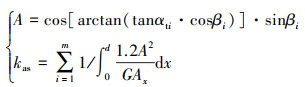
|
(10) |

|
(11) |
式中,Ix和Ax分别为距离齿根圆处的轮齿截面惯性矩和截面面积, 计算公式如下所示:
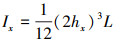
|
(12) |
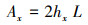
|
(13) |
式中, L为沿齿宽方向切分后每一片轮齿的厚度, 若齿宽被N等分, 则L=B/N, 其中B为齿宽, hx为接触点x到轮齿中心线的距离。
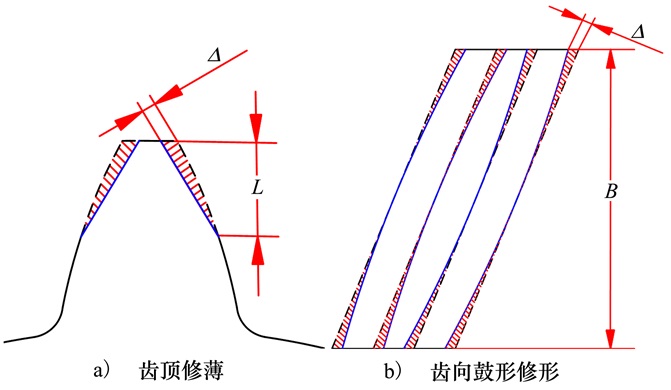
1.2 修形轮齿截面惯性矩和面积计算常用的修形方法为齿廓修形和齿向修形, 每种修形方法下包含几种不同的修形方式。本文采用的修形方式为: 齿廓修形为齿顶修薄, 修形曲线为直线; 齿向修形为鼓形修形, 修形曲线为抛物线, 如图 3所示。
|
| 图 3 修形方式及修形曲线 |
2种修形方式因为破坏了齿廓和齿向的曲线, 都会对重合度造成影响, 使得原本应该发生接触的地方不再接触, 导致某一时刻接触片数量m减小。本文先根据GB 3480-1983渐开线圆柱齿轮承载能力计算方法, 计算人字齿轮的平均刚度, 计算公式为
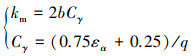
|
(14) |
式中:b为半齿宽;εα为端面重合度;q为单位齿宽柔度。
根据平均啮合刚度, 可以求得轮齿在载荷下的变形量, 使用变形量与每片轮齿理论啮合点处的修形量比较, 若修形量大于变形量, 说明该片轮齿不会发生接触。
修形还会改变接触点到轮齿中心线的距离hx, 从而使轮齿截面惯性矩Ix和截面面积Ax发生改变, 最终影响剪切刚度ks、弯曲刚度kb、轴向压缩刚度ka以及由轴向力引起的弯曲刚度kab和剪切刚度kas。下面对含有修形的接触点x到轮齿中心线的距离进行计算, 齿顶修薄将齿顶部分的齿廓修成一条直线, 带有齿廓修形的接触点x到轮齿中心线的距离公式为
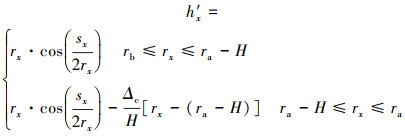
|
(15) |
式中:sx为任意圆齿厚;H为修形高度;Δc为齿廓修形量;ra为齿顶圆半径;rb为基圆半径。
(15) 式中, 任意圆齿厚sx可以由任意圆半径rx求出, 如果将轮齿沿着齿高的方向等分成M份, 可以用(15)式求出M个接触点x在对应半径处到轮齿中心线的距离。
在(15)式基础上, 计算得到含有齿向修形的接触点x到轮齿中心线的距离, 其公式为
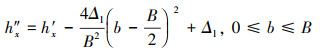
|
(16) |
式中:Δl为齿向修形量;B为齿宽。
(16) 式中的hx'是由(15)式求出的接触点x到轮齿中心线的距离, 在(15)式中, 沿着齿高方向将轮齿进行了M等分, 则根据hx'求出来的hx"也将是沿着齿高方向进行了M等分。如果将轮齿再沿着齿宽方向进行N等分, 自变量b就变成了一系列离散的值, 即b=(B/N)·i, 这样求出沿着齿宽方向不同等分点的hx"值。
将公式(16)计算得到的半齿厚代入公式(12)~(13)就可以计算出修形之后的截面惯性矩Ix和截面面积Ax。
1.3 综合刚度及时变啮合刚度计算将修形之后的截面惯性矩Ix和截面面积Ax代入公式(7)~(11)即可得到修形后的剪切刚度ks、弯曲刚度kb和轴向压缩刚度ka以及由轴向力引起的弯曲刚度kab和剪切刚度kas。此处所求的各个刚度是其中一个齿轮上轮齿的各个刚度, 如果要求单个轮齿的综合刚度, 计算公式如下所示
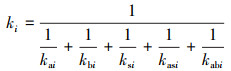
|
(17) |
式中, i=1, 2, 代表齿轮1或齿轮2。
要计算相互啮合的一对轮齿的综合刚度, 还要考虑赫兹接触刚度和齿轮基体刚度的影响, 但是由于人字齿轮的基体刚度比较大, 假设齿轮基体为刚性, 仅在综合刚度计算时考虑赫兹接触刚度, 计算公式如下
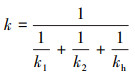
|
(18) |
式中:k为相互啮合的一对轮齿的综合刚度;k1和k2是由公式(17)计算出的2个齿轮上单个轮齿的综合刚度;kh为赫兹接触刚度。
通过(18)式算出的是单侧斜齿轮副一对轮齿的综合刚度, 根据啮合周期和重合度的关系, 将一对轮齿的综合刚度进行叠加, 得到单侧斜齿轮副的时变啮合刚度k(t)。假设人字齿轮为理想齿轮, 人字齿轮副时变啮合刚度应该为单侧斜齿轮副时变啮合刚度的2倍, 即kr(t)=2k(t), kr(t)为人字齿轮副时变啮合刚度。
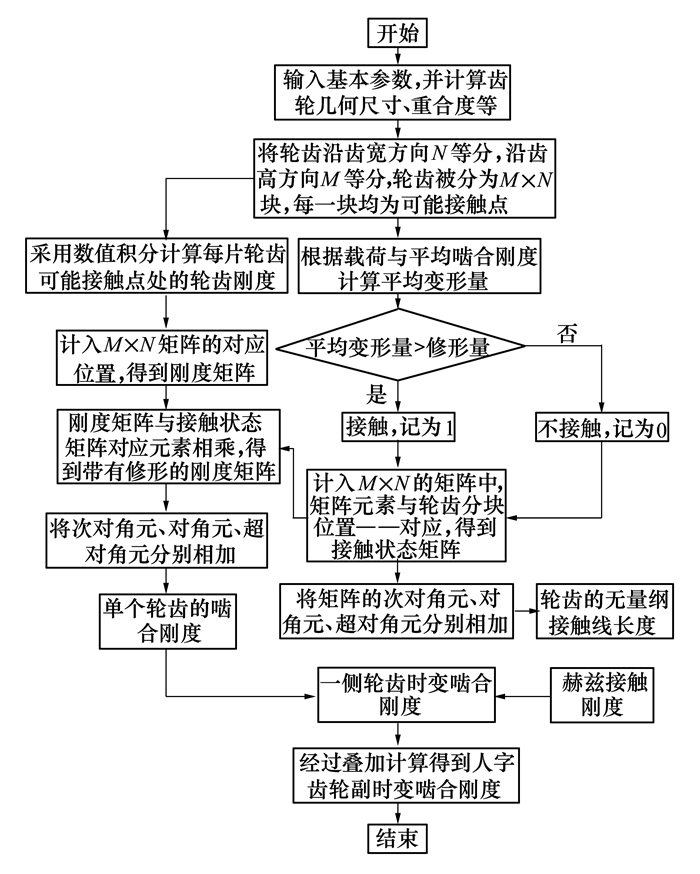
2 算法验证本文提出的考虑轴向力的修形人字齿轮副时变啮合刚度算法计算流程如图 4所示。
|
| 图 4 时变啮合刚度算法计算流程 |
用于验证该算法的正确性, 使用的人字齿轮和材料的基本参数如表 1所示。
| 参数及材料属性 | 数值 |
| 小齿轮齿数 | 34 |
| 大齿轮齿数 | 80 |
| 法向模数/mm | 5 |
| 法向压力角/(°) | 20 |
| 半齿宽/mm | 50/50 |
| 退刀槽宽度/mm | 58 |
| 螺旋角/(°) | 30 |
| 弹性模量/GPa | 210 |
| 切变模量/GPa | 80 |
| 泊松比 | 0.3 |
| 小齿轮转速/(r·min-1) | 1 000 |
| 转矩/(N·m) | 1 000 |
为了验证本文提出的解析法计算结果的可靠性和准确性, 将本文算法结果分别与有限元接触分析法得到的轮齿啮合刚度值和ISO标准得到的啮合刚度值进行对比。
使用ANSYS apdl语言对轮齿进行参数化造型, 得到两侧完全对称的一对轮齿的模型, 并进行网格划分, 得到一对轮齿的有限元模型如图 5所示。
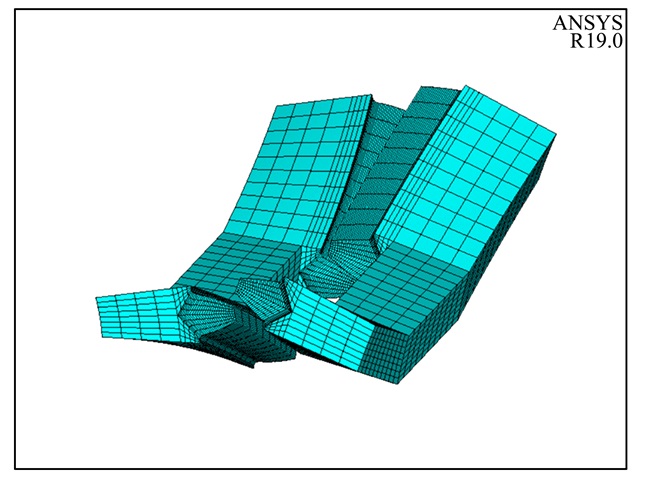
|
| 图 5 人字齿轮副一对轮齿有限元模型 |
建立有限元模型后, 对一个轮齿整个啮合过程中转过的角度进行等分, 然后调整啮合位置, 将调整后处于不同啮合位置的有限元模型导入workbench中进行边界条件设置和加载分析。
本文使用单齿啮合刚度并联方法求解一对轮齿的综合啮合刚度。因此在有限元计算时, 先将一个轮齿设置为刚体, 一轮齿设置为柔性体, 进行刚柔耦合计算, 得到一个轮齿的啮合刚度, 然后再将已经计算的轮齿设为刚体, 原先为刚体的轮齿设为柔性体, 再次进行计算, 得到另一个轮齿的啮合刚度, 2个轮齿的啮合刚度进行并联, 得到单对轮齿的综合啮合刚度。
在workbench中, 首先定义材料属性, 然后进入模型中将其中一个轮齿设为刚体, 另一个设为柔性体, 齿面接触为无摩擦接触, 将柔性轮齿2个侧面和轮毂处圆弧面进行固定约束, 刚性轮齿2个侧面和轮毂处圆弧面设置远端位置, 对这些面x, y, z方向的移动自由度和绕着x, y的2个转动自由度进行约束, 最后对刚性轮齿施加一个200 N·m的转矩, 施加边界条件后的模型如图 6所示。
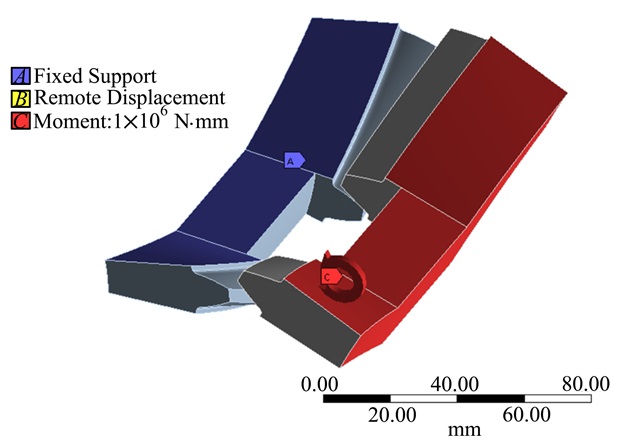
|
| 图 6 施加边界条件后的模型 |
分别对不同啮合位置的有限元模型进行求解后, 查看轮齿的总变形量δ, 通过公式
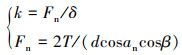
|
(19) |
计算出不同啮合位置的啮合刚度。其中, Fn为名义法向力。将仿真得到的轮齿的变形量带入公式(19), 计算得到单个轮齿啮合刚度, 并与本文计算的啮合刚度进行比较, 如图 7所示。

|
| 图 7 单齿啮合刚度对比 |
从图 7a)可以看出, 小齿轮单齿啮合刚度的有限元计算结果略小于本文计算结果, 但是趋势基本一致, 从图 7b)可以看出, 大齿轮单齿啮合刚度的有限元计算结果与本文计算结果比较接近。
将本文算法得到的人字齿轮副单对轮齿啮合刚度与ISO和有限元计算结果进行对比验证如图 8所示。

|
| 图 8 单对轮齿啮合刚度的对比验证 |
从图 8可以看出, 使用表 1中的参数, 在未修形及两侧完全对称的情况下, ISO标准计算得到的啮合刚度的最大值最大, 本文未考虑轴向力和考虑轴向力的计算结果均大于有限元计算结果, 这是由于有限元法中各离散单元之间具有耦合作用, 而本文解析算法并未考虑薄片之间的耦合作用。同时本文考虑轴向力的计算结果较未考虑轴向力的计算结果降低5.42%, 说明模型中考虑轴向力对啮合刚度的影响是有效的, 且考虑轴向力之后啮合刚度更加接近有限元结果。
3 修形对啮合刚度的影响本文针对表 1中的齿轮参数、材料属性及工况条件, 研究齿廓修形和齿向修形对人字齿轮副时变啮合刚度的影响。
3.1 齿廓修形量对啮合刚度的影响
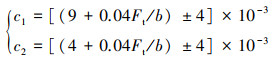
|
(20) |
式中:c1和c2分别为小齿轮和大齿轮的齿廓修量;Ft为切向力, b为齿宽;mn为法向模数。代入表 1中的参数得到小齿轮的修形量c1=0.017 mm, 大齿轮的修形量c2=0.012 mm。
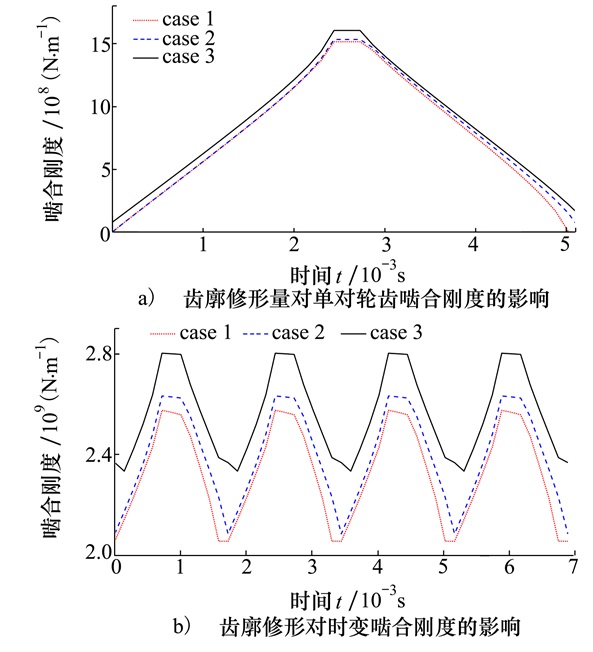
齿廓修形的影响因素有2个:①齿廓修形量;②齿廓修形长度。首先研究齿廓修形量对啮合刚度的影响, 一般齿廓修形长度为Lc=0.4mn, 文中大齿轮和小齿轮修形长度均取2 mm。然后在公式(20)计算得到的修形量基础上, 减小5 μm取一次修形量, 计算得到齿廓修形量对啮合刚度的影响, 如图 9所示。
|
| 图 9 齿廓修形量对啮合刚度的影响 |
图 9中, 情况1小齿轮齿廓修形量为0.017 mm, 大齿轮齿廓修形量为0.012 mm, 修形长度均为2 mm; 情况2小齿轮齿廓修形量为0.012 mm, 大齿轮齿廓修形量为0.007 mm, 修形长度均为2 mm; 情况3小齿轮和大齿轮均未修形。从图 9a)可以看出, 随着齿廓修形量的增加, 单对轮齿啮合刚度出现降低, 而且啮合刚度右侧明显降低较多, 这是因为小齿轮作为主动轮, 在退出啮合时, 小齿轮的顶部逐渐啮出, 而小齿轮的修形量较大, 会导致截面积减小较多, 使刚度降低较多, 甚至其修形量已经大于计算得到的平均变形量, 在进行接触判断时, 判定其为不接触, 即出现该处轮齿没有接触的情况, 则对应轮齿片的刚度记为0。从图 9b)可以看出, 随着齿廓修形量的增加, 时变啮合刚度减小。
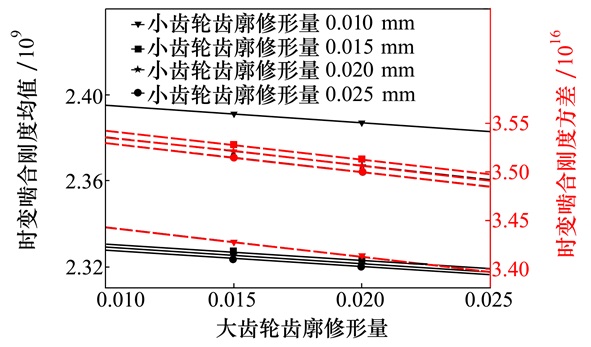
时变啮合刚度的方差可以体现出时变啮合刚度的波动情况, 不同修形量下时变啮合刚度的均值可以体现出修形对刚度大小的影响, 齿廓修形量对时变啮合刚度均值和方差的影响如图 10所示。
|
| 图 10 齿廓修形量对时变啮合刚度均值和方差的影响 |
图 10中实线为时变啮合刚度均值曲线, 可以看出, 随着小齿轮和大齿轮齿廓修形量的增加, 时变啮合刚度均值逐渐减小; 虚线为时变啮合刚度方差曲线, 当大齿轮齿廓修形量不变时, 随着小齿轮齿廓修形量的增加方差先增大后减小, 当小齿轮齿廓修形量不变时, 随着大齿轮齿廓修形量的增加, 方差逐渐减小。
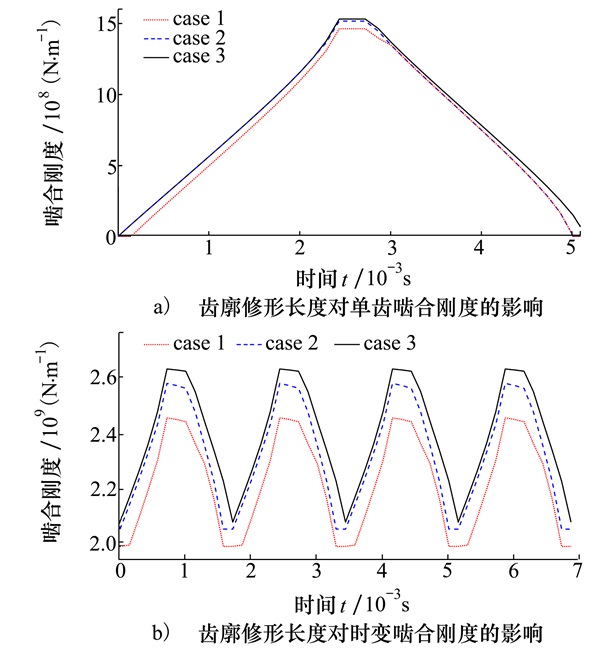
3.2 齿廓修形长度对啮合刚度的影响在小齿轮的修形量c1=0.017 mm, 大齿轮的修形量c2=0.012 mm保持不变的情况下, 使修形长度分别为1.5, 2.0, 2.5 mm, 研究修形长度对啮合刚度的影响, 如图 11所示。
|
| 图 11 齿廓修形长度对啮合刚度的影响 |
图 11中, 情况1齿廓修形长度为1.5 mm; 情况2齿廓修形长度为2.0 mm; 情况3齿廓修形长度为2.5 mm。从图 11可以看出, 与齿廓修形量对单齿啮合刚度的影响相似, 随着齿廓修形长度的增加单对轮齿啮合刚度和时变啮合刚度均减小。
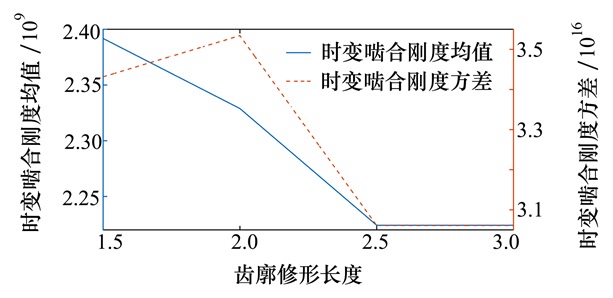
齿廓修形长度对时变啮合刚度均值和方差的影响如图 12所示。
|
| 图 12 齿廓修形长度对时变啮合刚度均值和方差的影响 |
图 12中实线为时变啮合刚度均值曲线, 可以看出, 随着齿廓修形长度的增加, 时变啮合刚度均值先下降, 然后逐渐平稳; 虚线为时变啮合刚度方差曲线, 随着齿廓修形长度的增加, 时变啮合刚到的方差先增大, 再减小, 最后趋于稳定。
3.3 齿向修形量对啮合刚度的影响齿向鼓形修形如图 3b)所示, 对于一般精度齿轮, 鼓形量计算公式为[22]
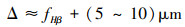
|
(21) |
式中, fHβ为螺旋线倾斜极限偏差。
通过查表可得, 小齿轮螺旋线倾斜极限偏差为8.5 μm, 大齿轮螺旋线倾斜极限偏差为9.0 μm, 通过(21)式计算, 得到小齿轮鼓形量的范围是13.5~18.5 μm, 大齿轮鼓形量的范围是14~19 μm, 本文小齿轮和大齿轮的鼓形量均取15 μm。为了研究鼓形量对啮合刚度的影响, 在选取的鼓形量两侧再取2个鼓形量进行对比较。
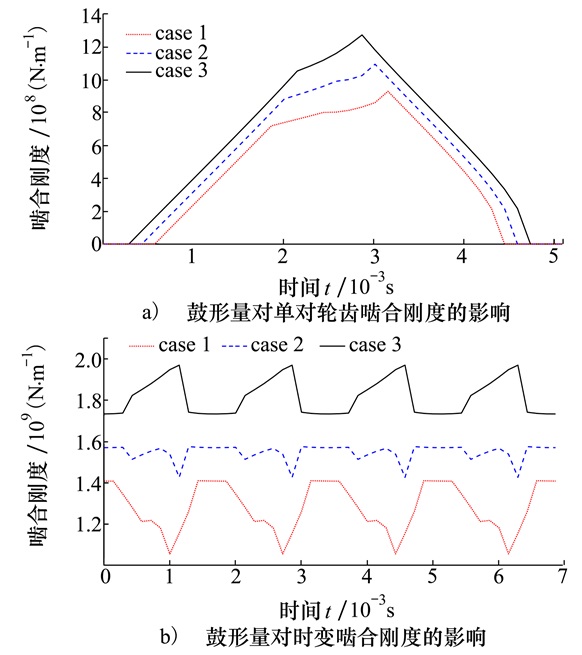
图 13中, 情况1小齿轮和大齿轮鼓形量均为10 μm; 情况2小齿轮和大齿轮鼓形量均为15 μm; 情况3小齿轮和大齿轮的鼓形量均为20 μm。从图 13a)可以看出, 随着鼓形量增加, 单对轮齿啮合刚度最大值明显降低, 而且啮合刚度两侧明显向内移动, 这是说明修形后导致啮合时, 存在更多轮齿不接触部分。从图 13b)可以看出, 随着齿向修形量增大, 时变啮合刚度不断减小, 刚度的幅值出现先减小后增大的趋势, 随着修形量增大, 时变啮合刚度由较大的波动变得平缓, 修形量增大到一定值后, 时变啮合刚度的波动又开始逐渐增大, 而且时变啮合刚度的波峰和波谷的位置出现变化。
|
| 图 13 齿向修形量对啮合刚度的影响 |
鼓形量对时变啮合刚度均值和方差的影响如图 14所示。
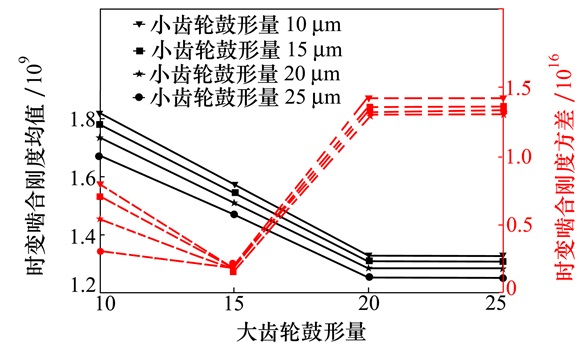
|
| 图 14 鼓形量对时变啮合刚度均值和方差的影响 |
图 14中实线为时变啮合刚度均值曲线,可以看出,随着小齿轮鼓形量的增加,时变啮合刚度均值逐渐减小,随着大齿轮鼓形量的增加,先逐渐减小然后趋于平稳;虚线为时变啮合刚度方差曲线,当小齿轮鼓形量不变时,随着大齿轮鼓形量的增加方差先减小后增大,然后趋于平稳,当大齿轮鼓形量不变时,随着小齿轮鼓形量的增加,方差逐渐减小。
3.4 与Masta软件的对比验证本文假设人字齿轮的退刀槽为刚性,然后将人字齿轮视为2个斜齿轮的并联,基于Masta对斜齿轮进行修形刚度分析。在使用Masta进行计算时,由于是对一侧斜齿轮进行计算,因此转矩需要减半,然后将Masta计算结果的2倍作为人字齿轮的啮合刚度,与本文的解析算法计算的含有修形的计算结果进行比较,齿廓修形结果比较如表 2所示,齿向修形结果比较如表 3所示。
| 齿廓修形量/μm | 齿廓修形长度/mm | 刚度最大值/109(N·m-1) | 误差/% | 刚度幅值/109(N·m-1) | 误差/% | ||||||
| 小齿轮 | 大齿轮 | 小齿轮 | 大齿轮 | 本文计算结果 | Masta计算结果 | 本文计算结果 | Masta计算结果 | ||||
| 0 | 0 | 0 | 0 | 2.80 | 2.78 | 0.72 | 0.46 | 0.38 | 17.39 | ||
| 12 | 7 | 2 | 2 | 2.63 | 2.62 | 0.38 | 0.55 | 0.44 | 11 | ||
| 17 | 12 | 2 | 2 | 2.58 | 2.52 | 2.33 | 0.52 | 0.42 | 19.23 | ||
| 17 | 12 | 1.5 | 1.5 | 2.63 | 2.56 | 2.66 | 0.52 | 0.43 | 17.31 | ||
| 17 | 12 | 2.5 | 2.5 | 2.45 | 2.51 | 2.45 | 0.46 | 0.40 | 13.04 | ||
| 齿向修形量/μm | 刚度最大值/109(N·m-1) | 误差/% | 刚度幅值/109(N·m-1) | 误差/% | ||||
| 小齿轮 | 大齿轮 | 本文计算结果 | Masta计算结果 | 本文计算结果 | Masta计算结果 | |||
| 10 | 10 | 1.97 | 1.90 | 3.55 | 0.24 | 0.28 | 16.67 | |
| 15 | 15 | 1.58 | 1.54 | 2.53 | 0.14 | 0.16 | 14.29 | |
| 20 | 20 | 1.41 | 1.52 | 7.80 | 0.35 | 0.31 | 11.43 | |
由表 2和表 3的对比可以看出,本文算法结果与Masta软件计算结果的2倍比较,刚度最大值的误差不超过8%,刚度幅值的误差不超过20%,说明该解析算法能够快速且较为准确对修形后的人字齿轮副的时变啮合刚度进行计算。
4 结论1) 将切片法与势能法相结合,提出了一种考虑对称度、轴向力和修形的人字齿轮传动时变啮合刚度的解析算法,并与有限元计算结果和ISO标准计算结果进行了比较,验证算法的准确性。
2) 单对轮齿啮合刚度及人字齿轮副时变啮合刚度均随着齿廓修形量的增大而减小,时变啮合刚度均值随着小齿轮和大齿轮齿廓修形量的增加逐渐减小,时变啮合刚度方差随着小齿轮齿廓修形量的增加先增大后减小,随着大齿轮齿廓修形量的增加逐渐减小。
3) 单对轮齿啮合刚度及人字齿轮副时变啮合刚度均随着齿廓修形长度的增大而减小,时变啮合刚度均值随着齿廓修形长度的增加先下降,然后逐渐平稳,时变啮合刚度方差随着齿廓修形长度的增加,先增大,再减小,最后趋于稳定。
4) 齿向修形对啮合刚度的降低较齿廓修形更为明显,单对轮齿啮合刚度及人字齿轮副时变啮合刚度均随着齿向修形量的增大而减小,时变啮合刚度均值随着小齿轮齿向修形量的增加逐渐减小,随着大齿轮齿向修形量的增加先减小最后趋于平稳,时变啮合刚度方差随着小齿轮齿向修形量的增加逐渐减小,随着大齿轮齿向修形量的增加先减小后增大,然后趋于平稳。
| [1] |
李润芳, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1997: 11-48.
LI Runfang, WANG Jianjun. Systematic dynamics of gear[M]. Beijing: Science Press, 1997: 11-48. (in Chinese) |
| [2] |
常乐浩, 刘更, 郑雅萍, 等. 一种基于有限元法和弹性接触理论的齿轮啮合刚度改进算法[J]. 航空动力学报, 2014, 29(3): 682-688.
CHANG Lehao, LIU Geng, ZHANG Yaping, et al. A modified method for determining mesh stiffness of gears based on finite element method and contact theory[J]. Journal of Aerospace Power, 2014, 29(3): 682-688. (in Chinese) |
| [3] |
刘文, 李锐, 张晋红, 等. 斜齿轮时变啮合刚度算法修正及影响因素研究[J]. 湖南大学学报, 2018, 45(2): 1-10.
LIU Wen, LI Rui, ZHANG Jinhong, et al. Study on correction algorithm of time-varying mesh stiffness of helical gears and its influencing factors[J]. Journal of Hunan University, 2018, 45(2): 1-10. (in Chinese) DOI:10.3969/j.issn.1008-1763.2018.02.002 |
| [4] |
毛汉成, 傅琳, 于广滨, 等. 考虑轮齿修形的变厚齿轮啮合刚度数值计算[J]. 计算机集成制造系统, 2022, 28(2): 1-10.
MAO Hancheng, FU Lin, YU Guangbin, et al. Numerical calculation of meshing stiffness for the beveloid gear with profile modification[J]. Computer Integrated Manufacturing Systems, 2022, 28(2): 1-10. (in Chinese) |
| [5] |
冯正玖, 靳广虎, 朱如鹏. 基于LTCA的直齿轮啮合刚度的计算与分析[J]. 机械传动, 2019, 43(8): 78-83.
FENG Zhengjiu, JIN Guanghu, ZHU Rupeng. Calculation and analysis of mesh stiffness of spur gear based on LTCA[J]. Journal of Mechanical Transmission, 2019, 43(8): 78-83. (in Chinese) |
| [6] | DAI He, LONG Xinhua, CHEN Feng, et al. An improved analytical model for gear mesh stiffness calculation[J]. Mechanism and Machine Theory, 2021, 159: 1-15. |
| [7] | HUI Ma, XU Pang, FENG Ranjiao, et al. Improved time-varying mesh stiffness model of cracked spur gears[J]. Engineering Failure Analysis, 2015, 55: 271-287. DOI:10.1016/j.engfailanal.2015.06.007 |
| [8] |
魏静, 赖育彬, 秦大同, 等. 齿廓修形斜齿轮副啮合刚度解析计算模型[J]. 振动与冲击, 2018, 37(10): 94-101.
WEI Jing, LAI Yubin, QIN Datong, et al. Analytical model of the mesh stiffness of helical gear pair after tooth profile modification[J]. Journal of Vibration and Shock, 2018, 37(10): 94-101. (in Chinese) |
| [9] |
王峰, 方宗德, 李声晋. 斜齿轮动力学建模中啮合刚度处理与对比验证[J]. 振动与冲击, 2014, 33(6): 13-17.
WANG Feng, FANG Zongde, LI Shengjin. Treatment and contrast verification of meshing stiffness in dynamic model of helical gear[J]. Journal of Vibration and Shock, 2014, 33(6): 13-17. (in Chinese) |
| [10] |
杨长辉, 徐涛金, 许洪斌, 等. 基于Weber能量法的直齿轮时变啮合刚度数值计算[J]. 机械传动, 2015, 39(2): 59-62.
YANG Changhui, XU Taojin, XU Hongbin, et al. Numerical calculation of time-varying meshing stiffness of spur gears based on Weber's energy method[J]. Journal of Mechanical Transmission, 2015, 39(2): 59-62. (in Chinese) |
| [11] |
孟宗, 石桂霞, 王福林, 等. 基于时变啮合刚度的裂纹故障齿轮振动特征分析[J]. 机械工程学报, 2020, 56(17): 108-115.
MENG Zong, SHI Guixia, WANG Fulin, et al. Vibration characteristic analysis of cracked faulty gears based on time-varying meshing stiffness[J]. Journal of Mechanical Engineering, 2020, 56(17): 108-115. (in Chinese) |
| [12] |
林腾蛟, 郭松龄, 赵子瑞, 等. 裂纹故障对斜齿轮时变啮合刚度及振动响应的影响分析[J]. 振动与冲击, 2019, 38(16): 29-36.
LIN Tengjiao, GUO Songling, ZHAO Zirui, et al. Influence of crack faults on the time-varying meshing stiffness and vibration response of helical gears[J]. Journal of Vibration and Shock, 2019, 38(16): 29-36. (in Chinese) |
| [13] | LIN T, OU H, LI R. A finite element method for 3D static and dynamic contact/impact analysis of gear drives[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(9/10/11/12): 1716-1728. |
| [14] | ZOUARI S, MAATAR M, FAKHFAKH T, et al. Three-dimensional analyses by finite element method of a spur gear: effect of cracks in the teeth foot on the mesh stiffness[J]. Journal of Failure Analysis and Prevention, 2007, 7(6): 475-481. |
| [15] | MA H, ZENG J, FENG R, et al. An improved analytical method for mesh stiffness calculation of spur gears with tip relief[J]. Mechanism and Machine Theory, 2016, 98: 64-80. |
| [16] | CHANG L, LIU G, WU L. A robust model for determining the mesh stiffness of cylindrical gears[J]. Mechanism and Machine Theory, 2015, 87: 93-114. |
| [17] | CUI L, ZHAI H, ZHANG F. Research on the meshing stiffness and vibration response of cracked gears based on the universal equention of gear profile[J]. Mechanism and Machine Theory, 2015, 94: 80-95. |
| [18] | CHEN Zaigang, SHAO Yimin. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011, 18(8): 2149-2164. |
| [19] | YI Yanga, HUA Niaoqing, TANG Jinyuan. Dynamic analysis for a spur geared rotor system with tooth tip chipping based on an improved time-varying mesh stiffness model[J]. Mechanism and Machine Theory, 2021, 165: 1-27. |
| [20] |
王峰, 朱彦霖, 方宗德, 等. 齿面修形对人字齿轮啮合刚度影响分析与试验研究[J]. 振动与冲击, 2018, 37(1): 40-46.
WANG Feng, ZHU Yanlin, FANG Zongde, et al. Theoretical and experimental investigation on the effect of teeth modification on the meshing stiffness of herringbone gear system[J]. Journal of Vibration and Shock, 2018, 37(1): 40-46. (in Chinese) |
| [21] |
林腾蛟, 陈梦寒, 杨金. 齿廓修形人字齿轮副时变啮合刚度计算方法[J]. 振动与冲击, 2021, 40(9): 94-101.
LIN Tengjiao, CHEN Menghan, YANG Jin. Calculation method of time-varying meshing stiffness of herringbone gear pair with tooth profile modification[J]. Journal of Vibration and Shock, 2021, 40(9): 94-101. (in Chinese) |
| [22] |
齿轮手册编委会. 齿轮手册[M]. 北京: 机械工业出版社, 2000: 143-150.
Gear Manual Editorial Board. Gear Handbook[M]. Beijing: China Machine Press, 2000: 143-150. (in Chinese) |
| [23] | WANG Qibin, ZHAO Bo, FU Yang, et al. An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component[J]. Mechanical Systems and Signal Processing, 2018, 16: 413-429. |
| [24] | WANG Siyu, ZHU Rupeng. An improved mesh stiffness model of helical gear pair considering axial mesh force and friction force influenced by surface roughness under EHL condition[J]. Applied Mathematical Modelling, 2022, 102: 453-471. |




