2. 空军工程大学 装备管理与无人机工程学院, 陕西 西安 710051
可靠性分析设计、优化的基础在于输入、输出不确定性的精确描述及传递。在航空、航天领域,各类结构、机构系统受到几何尺寸不准确性、材料参数分散性、载荷环境波动及仪器测量误差等不确定性因素影响,其零部件的性能、输出响应也存在一定变异特性。其中,有些参数因样本充足可构建精确概率分布,而有些参数难以评价,测量难,且样本缺乏(如航空安全、毁伤概率、健康指数)只能给定其变化区间[1]。为此,研究混合不确定性分析对可靠性设计、安全评价具有重要工程意义。
区间数据来源分为:①故障或者不确定性设备参与试验取得的数据;②来自不同专家的意见[2]。关于区间不确定性描述,Ferson等[3-4]将基于离散点概率分布估计推广至区间处理中,提出用概率盒描述区间数据。Zaman等[5]提出求解区间数据四阶矩的优化方法,并以此为约束用Jonson分布族描述区间数据。Williamson和Montgomery[6-7]分别在其博士论文讨论了贝叶斯概率盒以及用于概率盒区间计算的法则。Sankararaman等[8]用参数分布和非参数概率分布描述区间数据,并将其应用到区间不确定性传递。对于多类型数据混合不确定性分析,Elishakoff和Colombi[9]研究了不确定性概率模型和凸模型混合问题。曹鸿钧和段宝岩[10]提出一种非概率可靠性的度量指标,可用于椭球凸模型与区间变量并存情形。Qiu等[11]将区间分析方法引入传统概率理论中,研究了随机参数与区间参数并存结构可靠性问题。目前,概率理论可靠性模型发展比较成熟,而概率-区间混合模型的可靠性研究仍处于起步阶段,不确定性融合模型、模型求解算法等都值得深入研究。
根据极大熵原理[12]推断,在约束条件下描述变量不确定性的概率分布中熵值最大的分布具有最少偏见性。鉴于此,本文提出信息熵函数可用来度量离散点和区间数据包含的不确定性信息,且熵值越大,该组数据不确定性越大;反之,则越小。在此基础上,本文基于改进最大熵函数方法描述混合区间和离散数据的混合不确定性,得到包含混合不确定性信息的非参数概率分布,并在概率理论框架内,将不确定性由输入向输出传递,完成可靠性分析。
1 随机不确定性描述的传统最大似然函数法 1.1 随机不确定性描述模型随机不确定性模型以概率统计数学为基础,能够处理各种复杂环境下的不确定性传递问题,是目前使用范围最广、发展最为完善的不确定性理论。随机不确定性描述模型中当变量样本数据积累到足以精确确定变量概率密度函数时,可用概率密度函数形式定义[13]:
1) 连续型变量随机模型
假定随机变量X为连续型,且服从分布类型(正态、对数正态等)概率分布,概率密度函数为fX(x|θ),其中θ为概率分布参数,独立于随机变量。针对连续变量中单个离散点数据xi,视其为上下限几乎相等的退化区间,则单个离散点数据xi发生概率为:
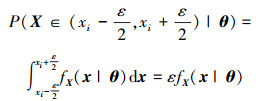
|
(1) |
式中,ε为任意小量(ε>0)。
若连续型变量总体为X={X1, X2, …, Xn},{X1, X2, …, Xn}是来自X的离散点样本,则{X1, X2, …, Xn}的联合分布律为
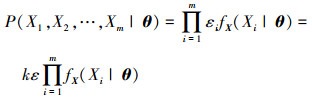
|
(2) |
式中:θ为待估计概率分布参数;k为正比例系数,其中k≠0。
2) 离散点数据随机模型
若总体X={X1, X2, …, Xn}属于离散型变量,且{X1, X2, …, Xn}是来自X的样本,则{X1, X2, …, Xn}的联合分布律为
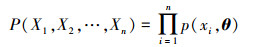
|
(3) |
式中:θ为待估计参数;P为变量X取其实现值x时的概率。
1.2 基于最大似然的随机不确定性描述对离散点的不确定性描述,最大似然函数法是常用的一种参数估计方法,基本思想是从模型总体随机抽取K组样本观测值,寻找最合理的参数估计量,能使抽取的该K组样本观测值的概率最大[14]。
传统最大似然函数法确定最优概率分布函数简要步骤具体见文献[14]。
传统方法处理离散点(样本规模较大时)不确定性,具有以下局限性:①需要人为确定数据概率分布类型,而数据绝大多数分布于密度函数“中部”(如正态分布),分布尾部是由“中间”分布外推得到; ②在结构可靠性分析中,起主要作用的恰是分布函数尾部,可靠性分析结果对变量分布尾部极为敏感。
因此,当要求可靠性较高(如失效概率Pf≤10-5)或缺乏数据时,假定概率模型方法适用性较差。
2 基于改进最大熵函数的混合不确定性描述熵可用作为不确定性的度量[15]。改进最大熵函数法继承概率和信息熵优点,其优势在于通过构造不同类型数据不确定性的联合熵函数,将由插值技术得到的非参数概率密度函数在原始数据空间上下限内均匀离散点处的概率密度值,作为优化自变量,建立优化模型,确定均匀离散点处的最优概率函数密度值,得到非参数概率密度函数。
2.1 熵熵是物质系统混乱和无序程度的测度,可用来描述信息不确定程度[15-17]。本文使用熵作为随机事件不确定性和信息量的量度。信息熵[16]认为随机变量不确定性越大,其熵值越大。因此,根据概率密度函数为fX(x)连续随机变量X,熵定义为
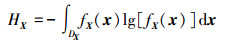
|
(4) |
式中:DX表示随机变量变化范围或支撑;fX(x)为随机变量X概率密度函数。
2.2 基于改进最大熵函数的混合不确定性描述针对区间[ai, bi], (i=1, 2, …, n)变量的熵,根据(4)式对多个混合区间联合熵函数定义
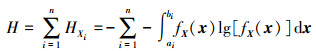
|
(5) |
针对包含m个离散点的随机变量X={X1, X2, …, Xm},其观测样本{x1, x2, …, xm},离散点可看作上下限近似相等退化区间,因此,单个离散点xi熵定义
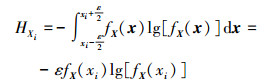
|
(6) |
式中,ε是任意小量(ε>0)。
根据(5)式和(6)式2种类型数据的熵定义,m个离散点x={x1, x2, …, xm}和n个区间[ai, bi], (i=1, 2, …, n)包含的混合不确定性熵函数可写为
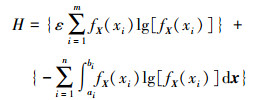
|
(7) |
变量包含区间和离散点数据信息的混合不确定性,(7)式联合熵函数可衡量原始数据包含不确定性信息量大小。
文献[17]认为描述随机事件概率分布fX(x)在约束条件下使得该组随机事件熵值最大,则该概率分布具有最少偏见。
2.3 基于插值技术的非参数概率密度函数优化相比于传统不确定性描述方法,本文优势在于基于极大熵[17]建立描述区间和离散点数据不确定性大小的联合熵函数优化模型,并巧妙地将优化变量转化为插值点的概率密度值。所提方法将传统对既定概率分布的参数估计转化为对原始数据空间自定义离散点处概率密度值估计优化,计算量和精度可通过自定义离散点数量控制,对原始数据不确定性信息挖掘更充分。在此基础上确定最少偏见概率密度函数fX(x),完成对多类型数据混合不确定性描述。本文应用插值技术得到非参数改进联合熵函数,将传统假定概率分布类型,分布参数估计寻优过程转化为在原始数据空间内对自定义随机离散点处的概率密度值优化,进而使用插值技术得到描述区间和离散点数据混合不确定性的最少偏见概率密度函数。具体过程如下:
1) 以离散点和区间数据中最大值和最小值作为原始数据空间上下限。区间上下限分别为A和B,表示为[A, B]。设x服从[A, B]上的均匀分布,通过在[A, B]均匀抽样,得到Q个离散点x={x1, x2, …, xQ},假定概率密度函数fX(x|θ)在Q个离散点处的初始值为f0={f10, f20, …, fQ0};
2) 根据离散点x={x1, x2, …, xQ}和对应离散点处概率密度函数值f0={f10, f20, …, fQ0},对概率密度函数fX(x)进行三次样条插值,得到非参数初始概率密度函数fX0(x);
3) 基于概率密度函数fX0(x),根据(7)式建立描述区间和离散点数据混合不确定性的联合熵函数;
4) 基于最大熵原理,建立优化模型如(8)式所示
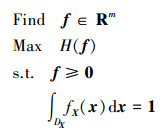
|
(8) |
式中: f∈Rm是概率密度函数在原始数据空间内上下限之间均匀离散点处的概率密度函数值,为设计变量; H(·)为目标函数。
5) 根据序列二次规划寻优算法求解优化模型,得到均匀离散点处的最优概率密度值为f*={f1*, f2*, …, fQ*};
6) 由离散点x={x1, x2, …, xQ}及其对应点处概率密度值f*={f1*, f2*, …, fQ*},使用三次样条插值,得到描述区间和离散点混合数据不确定性的最优非参数概率密度函数为fX*(x)。
采用序列二次规划算法求解(8)式中涉及的优化问题,在Matlab R2010b中,fmincon可实现该算法[18]。
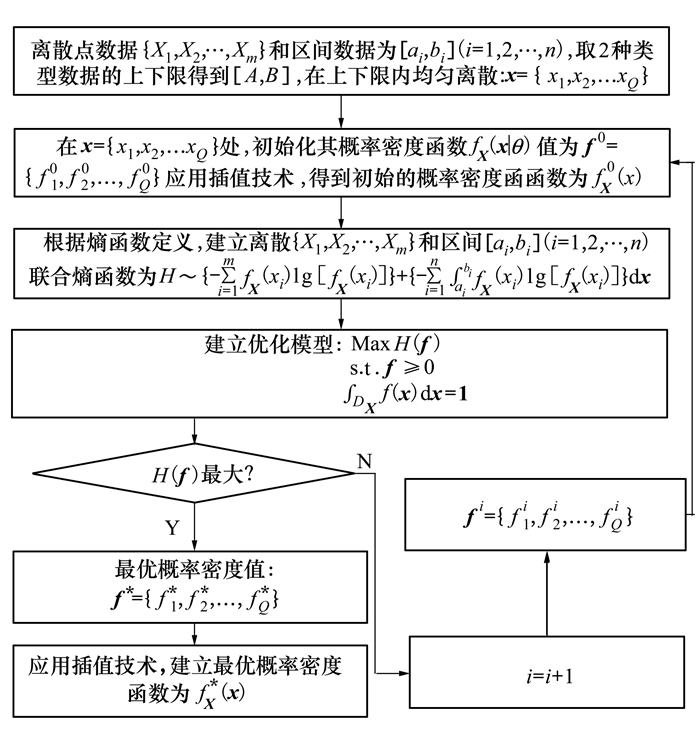
为了方便理解,将上述过程绘制成流程图,说明基于改进最大熵函数法描述混合不确定性的具体思路,如图 1所示。
|
| 图 1 改进最大熵函数描述混合不确定性方法优化流程图 |
在区间和离散点混合数据不确定性优化过程中,将传统针对假定分布类型概率分布参数的优化,转换为原始数据空间上下限内均匀离散点处概率密度值的优化,计算效率和精度可通过所选区间离散点的规模来控制。同时,所提方法是非参数的,避免了根据数据直方图判定分布类型,减少了人为误差。
3 算例本节通过2个算例说明所提方法对混合数据信息下不确定性描述的合理性。
3.1 数值算例1讨论一组区间与离散点的组合数据:X={[3.5, 4], [3.9, 4.1], [5,6], 4.1, 5.6, 3.8},其总区间为[3.5, 6],该组区间数据内包含离散点,本节将其视为上下限相等的退化区间。
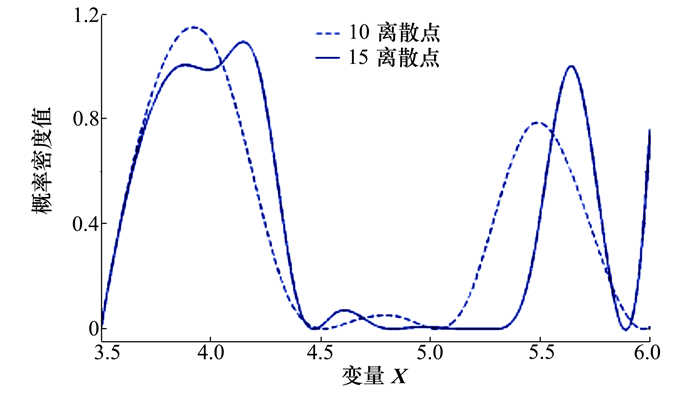
针对算例1,取Q=11为例,在原数据区间上下限上均匀离散后的样本为x=[3.5, 3.75, 4.0, 4.25, 4.5, 4.75, 5.0, 5.25, 5.5, 5.75, 6.0],基于改进最大熵函数法描述混合区间数据和离散点数据的不确定性,通过对联合熵函数进行最大值优化,得到均匀离散点处最优概率密度函数值为f*=[0.073 1, 0.120 3, 0.178 0, 0.007 7, 0.119 3, 0.142 4, 0.203 9, 1.735 4, 1.167 1, 0.172 5, 0.486 6]。按照上述步骤,取Q=15进行优化,得到类似结果。为更直观地表现该组区间和离散点数据的分布特点,用三次样条插值得到描述区间数据和离散点混合数据不确定性的概率密度函数,如图 2所示。
|
| 图 2 算例1基于改进最大熵函数描述混合不确定性的最优概率密度函数 |
图 2中分别给出了在原始数据区间内均匀离散点数为11和15情况下的优化结果。可以看到2种优化得到的概率密度函数都是双峰函数,峰值分别出现在[3.6, 4.4]和[5.3, 5.8]内,且其他区间内的概率密度明显小于峰值区间的概率密度值,这是因为长区间数据落在[3.6, 4.4]和[5.3, 5.8]内,造成概率集中。其中Q=15相比于Q=11,所得概率密度函数在对[3.9, 4.1]分布描述上更加精细。同时,在区间[5,6]和5.6离散点数据情况下,Q=15受到5.6离散点影响,概率密度函数右移,相比于Q=11更加科学。
此外,原始数据在[3.5, 4.2]区间内也有离散点数据和短区间数据分布,而图 3中概率密度函数在该处的概率密度值并不高,这是因为基于改进最大熵函数方法对区间数据包含的不确定性信息量给予了充分的熵值分配,认为区间数据包含不确定性信息量大于离散点数据的不确定性信息量,而且有学者认为区间数据可以看作是离散点数据的密集集合。注意到与初始数据相比,概率密度函数范围中包含了原数据中未包含的数据点,例如在4.5和3.0处其概率密度值并不等于零,而原数据中不包含该点。这是已经预见到的,因为基于改进最大熵函数的不确定性描述方法是依据原数据的统计分布特征对原数据样本进行合理扩展,生成的概率密度函数是描述原数据事件发生熵值最大的情况,即不确定性最大的情况,最大熵原理认为事物常处在最混乱无序的状态。此外,由于该方法使用了插值技术,在遵从原数据统计分布特征的前提下合理拓展了数据点,使其生成的概率密度函数具有更光滑的统计特征。
|
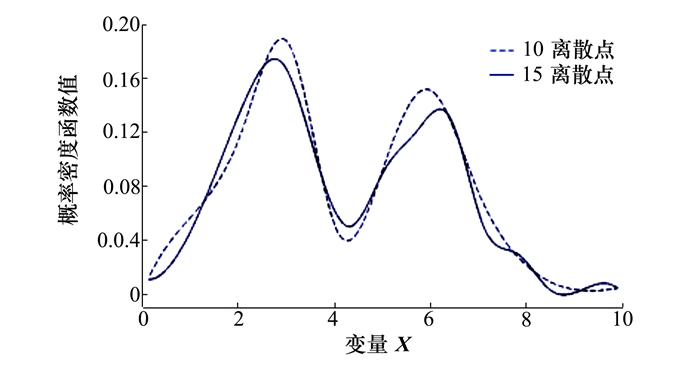
| 图 3 算例2改进最大熵函数描述混合不确定性的最优概率密度函数 |
讨论一组Ferson等研究过的区间数据[3]:X={[3.5, 6.4], [6.9, 8.8], [6.1, 8.4], [2.8, 6.7], [3.5, 9.7], [6.5, 9.9], [0.15, 3.8], [4.5, 4.9], [7.1, 7.9], 3.8, 4.9, 6.3},原数据区间为[0.15, 9.9]。
针对算例2,取Q=11,则在原数据区间上下限上均匀离散的样本为x=[0.15, 1.125, 2.1, 3.075, 4.05, 5.025, 6, 6.975, 7.95, 8.925, 9.9],基于改进最大熵函数方法描述混合区间数据和离散点数据的不确定性,得到区间内自定义离散点处最优概率密度函数值f*=[0.012 7, 0.061 1, 0.122 1, 0.183 6, 0.048 1, 0.093 2, 0.150 5, 0.078 1, 0.023 0, 0.004 1, 0.004 6]。按照上述步骤,取Q=15进行优化,得到类似结果。分别根据2次优化所得均匀离散点及其在离散点处的最优概率密度函数值,使用三次样条插值得到描述区间数据和离散点混合数据不确定性的概率密度函数, 如图 3所示。
图 3中分别给出了在原始数据区间内均匀离散点数为11和15情况下的优化概率密度函数,2个函数趋势大体是一致的,与原始数据分布特征相吻合。2种优化结果所得概率密度函数都是双峰函数,峰值分别出现在[2, 3.5]和[5.5, 7]内,且[2, 3.5]内的概率密度略大于[5.5, 7]区间,两者都明显大于其他区间内的概率密度值。这是因为在原始数据中有更多的数据落在[2, 3.5]和[5.5, 7]内,造成概率集中,符合原始数据的统计分布特征。根据图 3所示概率密度函数计算原始区间数据和离散点数据联合熵函数值最大,说明在该概率密度函数条件下,原始区间数据和离散点数据包含的不确定性信息最大,根据最大熵原理,这种数据状态出现的可能性最大。
4 区间数据和离散点混合数据不确定性传递Sandia国家实验室曾召开主观不确定性会议[19-20],研究者们讨论并交流了关于区间不确定性描述和传递问题的多种思路和方法。本节在对混合类型不确定性描述的基础上,尝试使用蒙特卡罗数值方法研究混合类型数据不确定在概率可靠性模型中的传递。事实上,若区间和离散点数据混合不确定性的概率化描述成功,则概率可靠性理论中众多成熟方法均可用于区间不确定性的传递[21-22]。
考虑不确定性经典算例[19-20]y=(a+b)a,输入变量a和b均为离散点和区间类型混合,分别为{[0.5, 0.7], [0.3, 0.8], [0.1, 1.0]}和{0.6, [0.4, 0.85], [0.2, 0.9], [0.0, 1.0]}。该问题是Sandia国家实验室召开区间不确定性会议讨论的实际问题之一,研究者们曾基于不同方法得到结果。
针对输入变量a和b中包含离散点和区间数据的混合不确定性,用改进最大熵函数法得到描述输入变量a和b不确定性的非参数概率密度函数,然后,根据输入变量概率密度函数进行蒙特卡罗数值模拟,获取输入变量a和b的随机样本。在概率可靠性理论框架下,对输入不确定性向输出传递,根据功能函数计算输出。最后,使用核密度法[23-24]估计输出的概率密度函数,对输出进行统计特征分析。具体过程如下:
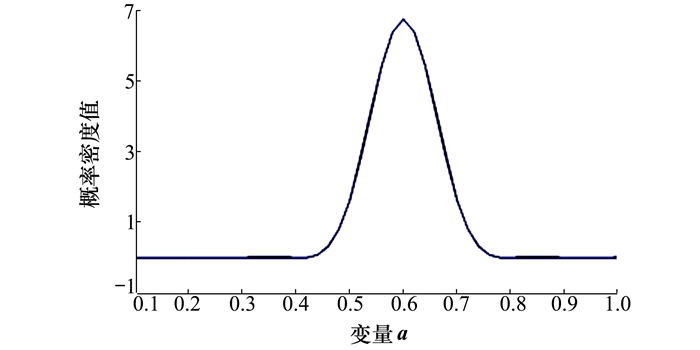
1) 基于改进最大熵函数法分别建立输入变量a和b的不确定性描述模型,得到输入变量a和b的非参数概率密度函数如图 4和图 5所示。
|
| 图 4 输入变量a的概率密度函数 |
|
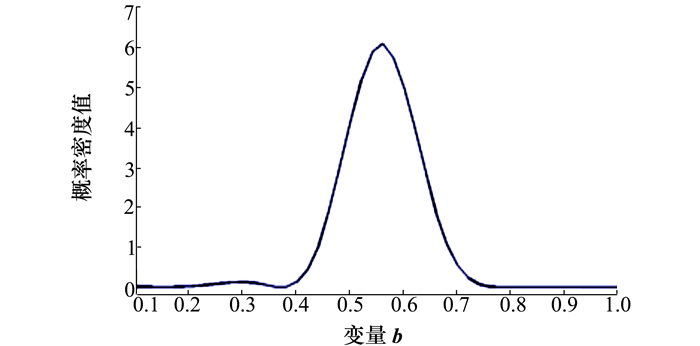
| 图 5 输入变量b的概率密度函数 |
图 4和图 5显示,输入变量a和b的概率密度函数均为单峰函数,峰值均出现在区间[0.4, 0.8]内,符合2组数据的统计特点,直观地显示了2组混合类型数据的分布状态。其中,输入变量a的概率密度函数有负值的出现,是因为插值技术保持数据统计特征的平滑所致。
2) 针对输入变量a和b,根据其非参数概率密度函数,进行蒙特卡罗模拟,得到输入变量a和b的5 000个随机样本。
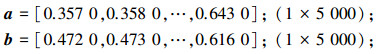
|
3) 在概率理论框架下,根据功能函数y=(a+b)a,将输入变量不确定性向输出传递,获取输出响应量y的随机样本。
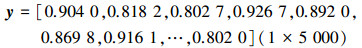
|
4) 针对输出响应量样本y,用核密度法估计输出响应量的概率密度函数,得到输出响应量的统计规律。核密度法[23-24]作为核估计理论中的分支在统计数据的非参数估计方面具有广泛的应用。对随机样本{X1, X2, …, Xn},其概率密度函数估计为
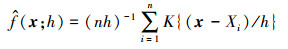
|
(9) |
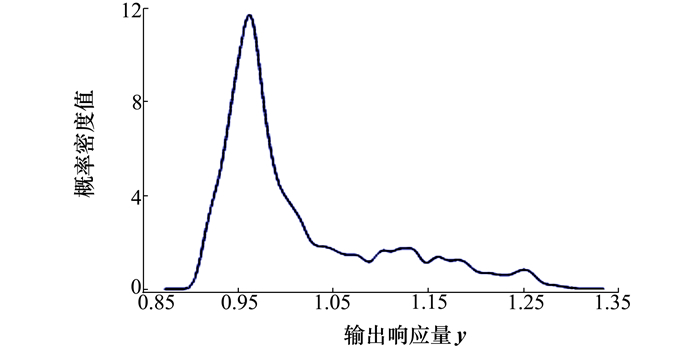
式中: K(·)为核函数, 满足∫K(x)dx=1;h为带宽,必须为正数。通常情况下,选择原点对称的单峰概率密度函数作为核函数,本节使用标准正态分布的概率密度函数作为核函数。带宽的选择则是研究者们重点研究的对象,其对密度函数的估计具有明显的影响,过大的带宽会造成过平滑估计,反之会造成欠平滑估计。带宽的选择需要考虑多方面的因素,本节目的在于讨论区间数据概率化描述的可行性,更侧重“定性”研究而不是“定量”研究,用核密度法估计输出响应量的概率密度函数, 如图 6所示。对于区间数据不确定性的传递问题,目前大多数研究工作得到的是响应量区间数据形式,例如在Sandia国家实验室召开的区间不确定性会议上[19-20],Kozine和Utkin、De Cooman和Troffaes、Ferson和Hajagos分别得到的结果为[0.9, 1.5], [1.0, 1.2], [0.8, 1.6]。但是所得到的区间并不能完全地反映出响应量的实际信息,即使在同一个区间内,不同点的可能性也是不同的。而针对区间数据和离散点混合数据不确定性,从概率和信息熵的观点出发,得到了描述输出响应量不确定性的概率密度函数,能够反映出输出响应量的分布情况,为成熟的概率理论应用于混合类型不确定性分析奠定了基础。
|
| 图 6 响应量y的概率密度函数 |
工程实际中,多数变量信息丰富能得到其概率分布,然而个别变量信息缺乏,只能确定其区间。因此,对不同类型变量的混合不确定性分析是十分必要的。针对该问题,本文研究了区间和离散点混合情况下联合不确定性描述,建立了混合类型不确定性数据联合熵函数,通过对基于插值技术的非参数概率密度函数在原始数据空间内均匀离散点处概率密度值的优化,得到混合不确定性的统一的概率化描述。相比于传统方法,所提方法是非参数的,将传统对假定分布的概率密度函数参数估计转化为对原始数据空间自定义离散点处概率密度值的优化,计算量和精度可通过自定义离散点数量控制,更充分地挖掘数据不确定性信息。
此外,对于区间不确定性传递,目前并没有公认的通用方法。研究者们曾分别从非概率和概率角度尝试提出了多种处理区间不确定性方法,值得注意是不同方法得到的结果尽管存在差异,但是在绝大多数情况中这种差异可接受。本文尝试将所提方法用于混合类型不确定性传递,分析输出响应的统计规律,完成可靠性分析,得到较合理结果。说明了所提方法在处理混合不确定性描述传递问题中具有一定潜力,值得进一步研究。
| [1] |
郭书祥, 吕震宙. 结构的非概率可靠性方法和概率可靠性方法的比较[J]. 应用力学学报, 2003, 20(3): 107-110.
GUO Shuxiang, LYU Zhenzhou. Comparison between the non-probabilistic and probabilistic reliability method for uncertain structure design[J]. Chinese Joural of Applied Mechanic, 2003, 20(3): 107-110. (in Chinese) DOI:10.3969/j.issn.1000-4939.2003.03.025 |
| [2] | BAUDRIT C, DUBOIS D. Practical representations of incomplete probabilistic knowledge. The fuzzy approach to statistical analysis[J]. Computational Statistical & Data Analysis, 2006, 51(1): 86-108. |
| [3] | FERSON S, KREINOVICH V, HAJAGOS J, et al. Experimental uncertainty estimation and statistics for data having interval uncertainty[R]. SAND-2007-0939 |
| [4] | FERSON S, TUCKER W T. Sensitivity in risk analyses with uncertain numbers[R]. SAND-2006-2801 |
| [5] | ZAMAN K, RANGAVAJHALA S, MCDONALD M P, et al. A probabilistic approach for representation of interval uncertainty[J]. Reliability Engineering and System Safety, 2011, 96: 117-130. DOI:10.1016/j.ress.2010.07.012 |
| [6] | WILLIAMSON R C. Probabilistic arithmetic[D]. Brisbane: University of Queensland, 1989 |
| [7] | MONTGOMERY V. New statistical methods in risk assessment by probability bounds[D]. Durham: Durham University, 2009 |
| [8] | SANKARARAMAN S, MAHADEVAN S. Likelihood-based representation of epistemic uncertainty due to sparse point data and/or interval data[J]. Reliability Engineering and System Safety, 2011, 96: 814-824. DOI:10.1016/j.ress.2011.02.003 |
| [9] | ELISHAKOFF I, COLOMBI P. Combination of probabilistic and convex models of uncertainty when scare knowledge is present on acoustic excitation on parameters[J]. Computer Methods in Applied Mechanics and Engineering, 1993, 104: 187-209. DOI:10.1016/0045-7825(93)90197-6 |
| [10] |
曹鸿钧, 段宝岩. 基于凸集合模型的非概率可靠性研究[J]. 计算力学学报, 2005, 22(5): 546-549.
CAO Hongjun, DUAN Baoyan. An approach on the non-probabilitic reliability of structures based on uncertainty convex models[J]. Chinese Joural of Computational Mechanics, 2005, 22(5): 546-549. (in Chinese) |
| [11] | QIU Z P, YANG D, ELISHAKOFF I. Probabilistic interval reliability of structural systems[J]. International Journal of Solids and Structures, 2008, 45: 2850-2860. DOI:10.1016/j.ijsolstr.2008.01.005 |
| [12] | SOIZE C. Maximum entropy approach for modeling random uncertainties in transient elastodynamics[J]. Journal of Acoustical Society of America, 2001, 109(5): 1979-1996. DOI:10.1121/1.1360716 |
| [13] |
吕震宙, 宋述芳, 李洪双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.
LYU Zhenzhou, SONG Shufang, LI Hongshuang, et al. Reliability and reliability sensitivity analysis of uncertainty structure[M]. Beijing: Science Press, 2009. (in Chinese) |
| [14] |
赵宇. 可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2011.
ZHAO Yu. Data analysis of reliability[M]. Beijing: Beihang University Press, 2011. (in Chinese) |
| [15] | REZA F M. An introduction to information theory[M]. New York: Dover Publications, 1994. |
| [16] | SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27: 379-423. DOI:10.1002/j.1538-7305.1948.tb01338.x |
| [17] | SOIZE C. Maximum entropy approach for modeling random uncertainties in transient elastodynamics[J]. Journal of Acoustical Society of America, 2001, 109(5): 1979-1996. DOI:10.1121/1.1360716 |
| [18] |
龚纯, 王正林. Matlab语言常用算法程序集[M]. 北京: 电子工业出版社, 2011.
GONG Chun, WANG Zhenglin. Programs collection of algorithm in common use based on Matlab[M]. Beijing: Publishing House of Electronics Industry, 2011. (in Chinese) |
| [19] | OBERKAMPF W L, HELTON J C, JOSLYN C A, et al. Challenge problems: uncertainty in system response given uncertain parameters[J]. Reliability Engineering and System Safety, 2004, 85: 11-19. DOI:10.1016/j.ress.2004.03.002 |
| [20] | FERSON S, JOSLYN C A, HELTON J C. Summary from the epistemic uncertainty workshop: consensus amid diversity[J]. Reliability Engineering and System Safety, 2004, 85: 355-369. DOI:10.1016/j.ress.2004.03.023 |
| [21] | ZHANG F, XU X, WANG L, et al. Global sensitivity analysis of twostage thermoelectric refrigeration system based on response variance[J]. Intentional Journal of Energy Research, 2020, 44: 6623-6630. DOI:10.1002/er.5398 |
| [22] |
吕震宙, 李璐祎, 宋述芳. 不确定性结构系统的重要性分析理论与求解方法[M]. 北京: 科学出版社, 2016.
LYU Zhenzhou, LI Luyi, SONG Shufang. Importance analysis theory and solution method of uncertain structural system[M]. Beijing: Science Press, 2016. (in Chinese) |
| [23] | BOTEV Z I, GROTOWSKI J F, KROESE D P. Kernel density estimation via diffusion[J]. The Annals of Statistics, 2010, 38: 2916-2957. |
| [24] | BOTEV Z I. Kernel density estimation using Matlab[EB/OL]. (2015-12-30)[2020-09-19]. http://www.mathworks.us/matlabcentral/fileexchange/authors/27236 |
2. Equipment Management and UAV Engineering College, Air Force Engineering University, Xi'an 710051, China



