2. 上海大学 机电工程与自动化学院, 上海 200072;
3. 北京交通大学 机械与电子控制工程学院, 北京 100044
薄壁结构由于质量轻, 广泛应用于航空、航天领域, 如太阳能帆板、飞机的机翼和舱体等。单一功能的薄壁结构极易发生振动与变形, 且结构阻尼低、不稳定[1]。压电阻尼层合结构具有被动阻尼和主动致动性能, 也称为主被动结构, 具有良好的力学特性, 广泛应用于形状控制、振动控制、噪声控制等方面[2]。黏弹性阻尼材料特殊的物理性能, 使得主被动阻尼层合结构拥有复杂的层间物理特性, 增加了主被动阻尼层合结构动力学建模难度, 且不易实现。
最早Kerwin等[3]对黏弹性材料的阻尼参数进行了定量分析, 并提出了阻尼材料的损耗因子。王金朝等[4]采用多输入多输出锤击法对约束阻尼板进行模态实验并与有限元结果互相验证。陈威和夏利娟[5]基于模态应变能法推导出模态损耗因子的修正公式, 结果表明阻尼加筋板的阻尼弹性模量频变效应对模态损耗因子影响明显, 阻尼材料的弹性模量可取为定值。黄微波等[6]研究了阻尼层合结构的层间厚度对约束阻尼结构振动性能带来的影响, 结果表明约束层厚度与基层厚度相等时结构复合损耗因子最大, 并且随着基层厚度与约束层厚度之比逐渐减小, 厚度比对结构损耗因子的影响也变小。Jin等[7]对黏弹性阻尼夹层复合矩形板的振动和阻尼进行了分析, 基于Reddy的高阶剪切理论, 并且考虑了弯曲-拉伸、弯曲-扭转、拉伸-扭转以及泊松效应等不同情况下的材料耦合情况。
阻尼层合圆柱状壳体结构在工程中的应用也很广泛。Mokhtari等[8]利用Rayleigh-Ritz方法提出了夹层圆柱壳的一个计算公式, 讨论了关键参数对动力性能的影响。Yang等[9]研究了中间夹层为黏弹性材料的复合材料板的超音速颤振阻尼效应。Huang等[10]建立了2种基于剪切和压缩阻尼机制的夹层结构分析模型, 并说明了这2种不同阻尼机制的适用范围。Ebrahimi和Barati[11]建立了一个非局部应变梯度板模型, 研究了黏弹性、非局部参数、电压等因素对压电阻尼层合板振动特性的影响。
通过文献调研可知, 多数文献集中于阻尼层合板结构的研究, 对于在工程中应用前景很广的压电阻尼层合壳体结构研究较少。本文拟构建基于zig-zag板壳假设的“机-电”耦合压电阻尼层合结构有限元模型。用文献数据验证模型的正确性, 并进一步研究材料增强角度、阻尼层厚度和结构曲率对压电阻尼层合结构频率和损耗系数的影响, 可以为压电阻尼层合结构的减振降噪及结构设计提供必要的理论基础。
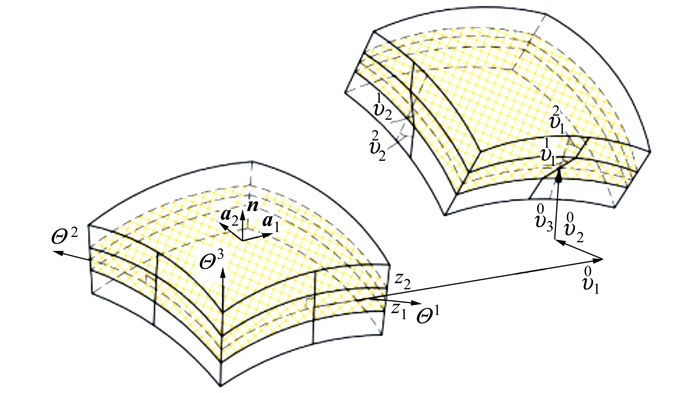
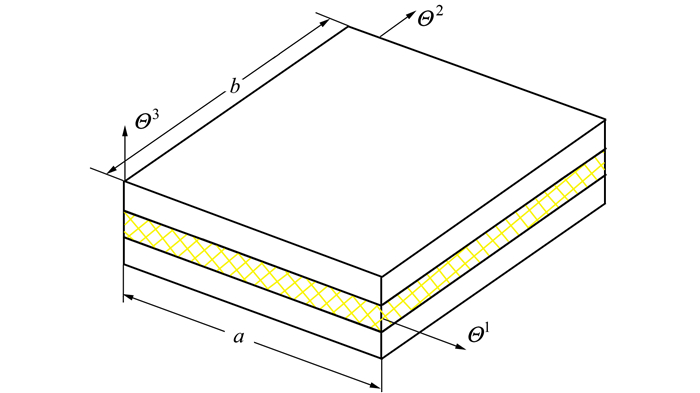
1 压电阻尼层合结构阻尼结构中黏弹性层的弹性模量远小于其他弹性层的弹性模量, 一般相差5~7个数量级。此时结构变形前垂直于中性面的线在变形后已经不是直线。为了能够准确地对黏弹性阻尼结构进行仿真, 需要构建基于zig-zag板壳变形假设的应变位移关系。zig-zag板壳变形假设示意图如图 1所示, 黏弹性阻尼层的变形量明显大于一般弹性层的变形量。图 1中的a1, a2和n表示中性面任意点分别沿Θ1, Θ2和Θ3方向的基矢; z1和z2分别表示黏弹性阻尼层下表面和上表面的Θ3坐标值。运动参数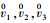
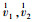
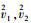
|
| 图 1 结构变形与自由度表示 |
则板壳结构上任意点的位移向量u可以用7个运动学参数表示为
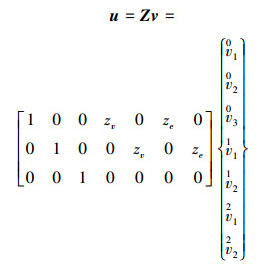
|
(1) |
式中: v为位移向量; Z为变换矩阵, 其中zv和ze值取决于计算的结构位置, 如表 1所示。
假设结构在厚度方向上不可压缩, 这时Green-Lagrange应变张量主要由面内应变εαβ和横向剪切应变εα3组成, 可以写为[12]
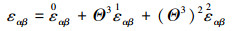
|
(2) |
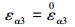
|
(3) |
(2) 式与(3)式中各应变分量与位移场之间的关系可以表示为:
1) 对于计算结构位置Θ3≤z1与Θ3≥z2

|
(4) |

|
(5) |
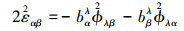
|
(6) |
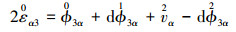
|
(7) |
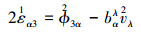
|
(8) |
计算Θ3≤z1时d=z1, 计算Θ3≥z2时d=z2。
2) 对于计算结构位置z1 < Θ3 < z2
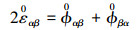
|
(9) |
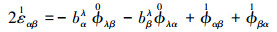
|
(10) |
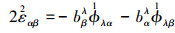
|
(11) |

|
(12) |
式中
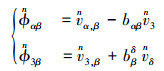
|
(14) |
下标‘, β’为对Θβ的空间导数, 作为下标α, β, λ, δ取值为1和2, 头标‘n’的取值为0, 1和2。另外, bαβ和bβδ分别为协变和混合曲率张量, 对于平板结构来说曲率张量全部为零; 对于柱状板壳结构来说只有b22=R和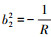
压电阻尼层合结构机电耦合有限元本构方程的矩阵形式为
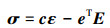
|
(15) |
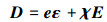
|
(16) |
式中,σ, ε, D和E分别表示应力向量、应变向量、电位移向量和电场向量。此外, c为弹性常数矩阵, 其与压电常数矩阵d和e之间的关系可以用矩阵形式表示为e=dc, χ为介电常数矩阵。
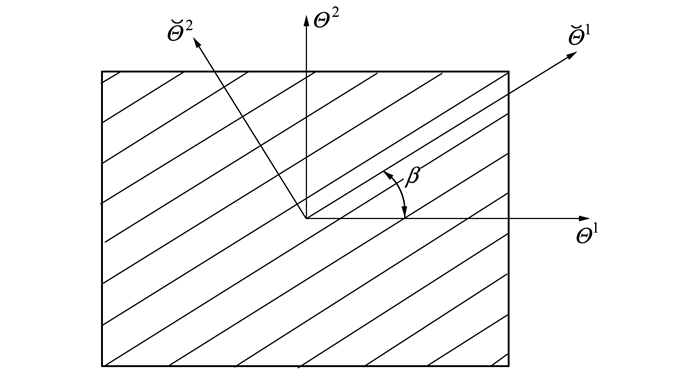
对于正交异性的材料, 用(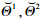
|
| 图 2 局部坐标系和材料坐标系 |
对于材料坐标系(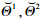

|
(17) |
式中,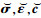
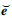
采用Hamilton原理来推导压电阻尼层合结构的动力学方程, 可以表述为从t1到t2的虚功积分等于零, 即
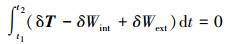
|
(18) |
式中,δT为压电阻尼层合结构的动能微分, 可以表示为
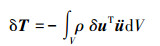
|
(19) |
式中:δ表示变分运算符;ρ为材料密度;ü表示u对时间的二阶导数。内力功的变分δWint可以表示为
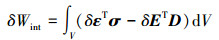
|
(20) |
外力功的变分可以表示为
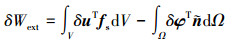
|
(21) |
式中: fs为面力力向量; φ表示压电片电极产生的电势向量; 
将(19)~(21)式代入(18)式可以得到压电阻尼层合结构的机电耦合动力学有限元方程
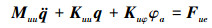
|
(22) |
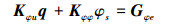
|
(23) |
式中:q为节点自由度向量;Muu, Kuu, Kuφ和Kφφ分别为总质量矩阵、刚度矩阵、耦合刚度矩阵和压电矩阵; Fue和Gφe为外力和电场向量。
3.3 阻尼材料模型与复刚度矩阵通常认为阻尼材料的弹性模量是复弹性模量, 表示为
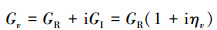
|
(24) |
弹性模量实部GR称为储能模量, 弹性模量虚部GI称为损耗模量, ηv表示阻尼材料的损耗因子。则结构的总刚度矩阵Kuu可以写为
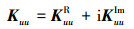
|
(25) |
压电阻尼层合结构的自然频率f和损耗系数η可表达为
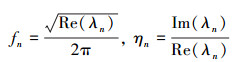
|
(26) |
式中,λn是第n阶复特征角频率。弹性层的阻尼矩阵用CS表示, 根据Moita等[14]使用的方法来求解阻尼材料的阻尼矩阵CV, 可以表示为

|
(27) |
根据(25)式和(27)式, (22)式可以整理为
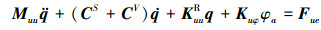
|
(28) |
采用如图 3所示的对称阻尼层合板与文献[15]的固有频率和损耗系数结果进行对比。板的尺寸为348 mm×304.8 mm×0.762 mm, 中间阻尼层厚度为0.254 mm。阻尼材料的损耗系数ηv为常数0.5, 阻尼层与弹性层的材料参数如表 2所示。
|
| 图 3 阻尼层合结构示意图 |
采用12×10网格划分, 八节点矩形单元, 两短边简支(simply supported: S), 两长边固支(clamped: C), 即CSCS。且认为压电材料在无外电场情况下为闭环状态。则结构前5阶固有频率f和结构损耗系数η数据对比如表 3所示, 仿真结果与文献结果吻合较好。
压电阻尼层合壳体结构如图 4所示, 半径用R表示, 压电层厚度为1 mm, 复合弹性层(T300/976)的厚度为1.5 mm, 宽度W=160 mm, 中性面弧长为314 mm。复合材料(T300/976)和压电层的材料参数在表 4中列出, 且认为它们为弹性层。阻尼材料参数如表 2所示。在Θ1和Θ2方向上分别划分了8个和10个网格, 采用七自由度八节点的矩形单元。

|
| 图 4 压电阻尼层合壳示意图 |
| T300/976 | 压电层 |
| Y1=150 GPa | Y=67 GPa |
| Y2=95 GPa | υ=0.33 |
| υ12=υ23=0.3 | ρ=7 800 kg/m3 |
| G12=G13=7.1 GPa | d31=-1.711 9×10-10 m/F |
| G23=2.5 GPa | d32=-1.711 9×10-10 m/F |
| ρ=1 600 kg/m3 | ϵ33=2.03×10-8 F/m |
壳体两直边固支, 其余简支, 即CSCS。令结构半径R=100 mm, 阻尼层的厚度为1 mm, 复合弹性层(T300/976)的增强角度β变化范围为0°~90°, 结果如表 5所示。当增强角度增加到55°时, 第一阶结构频率f1逐渐增加, 随着增强角度继续增加, 频率开始缓缓降低, 而第一阶损耗因子η1一直处于下降状态; 角度从0°逐渐变化到90°时, 第二阶频率f2一直增加, 第二阶损耗因子η2整体呈降低趋势。
| β/(°) | f1 | η1/% | f2 | η2/% |
| 0 | 1 291.02 | 1.399 | 1 318.44 | 1.440 |
| 5 | 1 294.14 | 1.387 | 1 321.81 | 1.425 |
| 10 | 1 303.29 | 1.352 | 1 331.70 | 1.382 |
| 15 | 1 317.91 | 1.299 | 1 347.47 | 1.315 |
| 20 | 1 337.08 | 1.232 | 1 368.08 | 1.229 |
| 25 | 1 359.59 | 1.156 | 1 392.14 | 1.132 |
| 30 | 1 384.10 | 1.077 | 1 417.94 | 1.030 |
| 35 | 1 409.33 | 0.999 | 1 443.48 | 0.927 |
| 40 | 1 434.31 | 0.924 | 1 466.48 | 0.829 |
| 45 | 1 458.39 | 0.852 | 1 484.74 | 0.739 |
| 50 | 1 481.17 | 0.784 | 1 496.64 | 0.664 |
| 55 | 1 501.74 | 0.605 | 1 502.17 | 0.720 |
| 60 | 1 500.91 | 0.562 | 1 520.70 | 0.660 |
| 65 | 1 495.92 | 0.533 | 1 535.87 | 0.605 |
| 70 | 1 488.81 | 0.514 | 1 546.88 | 0.557 |
| 75 | 1 481.37 | 0.502 | 1 553.50 | 0.519 |
| 80 | 1 474.99 | 0.496 | 1 556.39 | 0.492 |
| 85 | 1 470.69 | 0.493 | 1 557.05 | 0.476 |
| 90 | 1 469.17 | 0.492 | 1 557.05 | 0.471 |
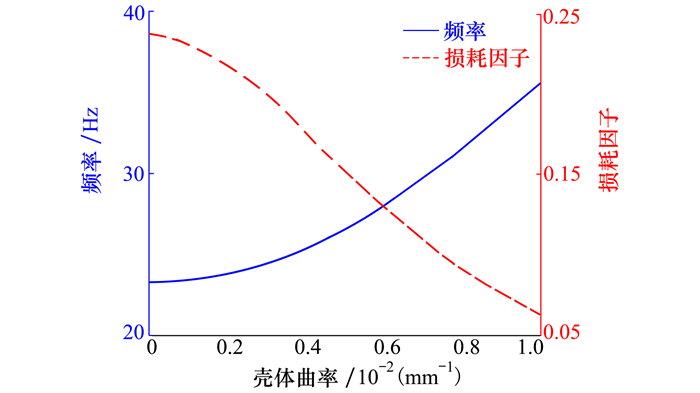
只固定壳体左边的一条直边, 其余边为自由状态(Freedom: F), 即边界条件为CFFF, 壳体的曲率半径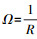
|
| 图 5 曲率Ω对结构频率f和损耗因子η的影响 |
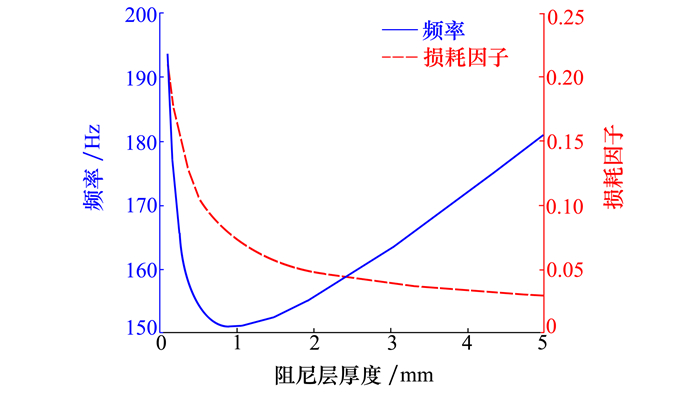
同时固定压电阻尼层合壳体的2条直角边, 即边界条件为CFCF。结构的半径R为100 mm, 增强角度β=0°保持不变, 而阻尼层厚度从0.1 mm逐渐增加至5 mm。结果如图 6所示, 当阻尼层厚度从0.1 mm增加到约1 mm时, 频率降低非常快, 而当阻尼层厚度继续增加时, 频率开始缓慢增加; 而损耗系数在阻尼层厚度从0.1~5 mm时一直减小, 但减小的速度越来越慢。即阻尼层厚度对结构特性的影响并不是单调递增或单调递减的。
|
| 图 6 阻尼层厚度对结构频率f和损耗因子η的影响 |
本节研究边界条件为CFFF的压电阻尼层合壳体(见图 4)的静力和动力学特性。令壳的半径R=100 mm, 阻尼层的厚度为0.5 mm和增强角度β=0°。其他尺寸、材料、单元类型和网格划分与4.2节相同。压电片黏贴面的电势为零, 且整个上表面都是等电位的。对壳体结构施加150 V电压, 壳体结构在Θ2方向上中心线位移如图 7静力学响应所示, 壳体距离固定端越远, 节点位移就越大。

|
| 图 7 压电阻尼层合壳体的静力和动力学响应 |
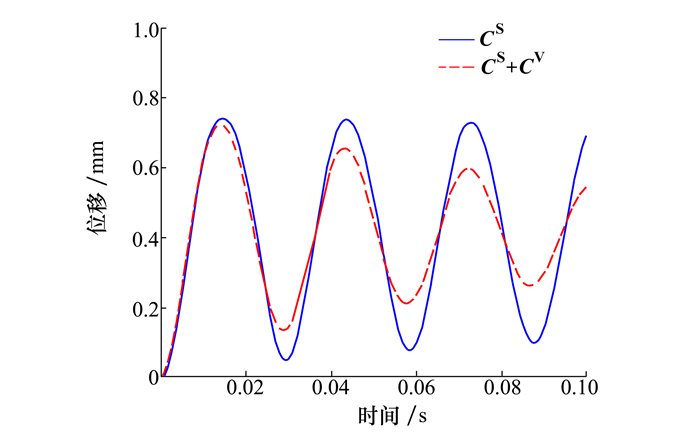
对结构施加电压后, 结构会在一个范围内来回振动。由图 5可知壳体的频率为35.8 Hz, 取0.1 s即3.58个振动周期来研究该壳体的动力学特性。不考虑阻尼情况下自由端中间节点的环向振动响应如图 7所示。现实中结构不会一直振动下去, 结构会逐渐趋于平稳, 这个过程是阻尼效应作用的结果。不同阻尼效应情况下壳体的自由端中间节点的环向振动, 结果如图 8所示。图例中CS表示只考虑了结构自身的阻尼效应; CS+CV则表示既考虑了结构自身的阻尼效应又考虑了黏弹性结构的阻尼效应。可以看出黏弹层阻尼可以使结构的振动衰减很快, 对抑制结构振动有很好的效果。
|
| 图 8 压电阻尼层合壳体的环向振动阻尼效应 |
基于zig-zag假设构建了压电阻尼层合结构机电耦合动力学和静力学模型, 实现层间材料参数差异巨大的准确计算。与参考文献算例数据对比验证模型正确性后, 使用建立的模型对压电阻尼层合壳体结构进行了静力学和动力学分析, 得出:
1) 增强角度在0°~90°逐渐增加时, 当增加到约55°时, 结构频率逐渐增加, 之后频率随着增强角度的增加而缓缓降低; 而损耗因子一直处于降低状态。
2) 压电阻尼层合壳体结构的曲率从0增加到0.01 mm-1时, 壳体结构的频率增加, 而损耗系数逐渐减小。
3) 当阻尼层厚度从0.1 mm增加到约1 mm时, 频率降低非常快, 随着厚度继续增加, 频率反而缓慢增加; 而损耗系数在阻尼层厚度从0.1~5 mm时减小的速度持续降低。4) 研究不同阻尼效应下壳体自由端的环向振动得出黏弹层阻尼可以使结构的振动衰减很快, 有很好的减振效果。
本文的研究结果对压电阻尼层合结构的设计和使用具有指导意义和参考价值。
| [1] |
孙大刚, 赵树萍, 孟杰, 等. 风力机叶片约束阻尼结构建模及抑颤研究[J]. 太阳能学报, 2018, 39(4): 1165-1172.
SUN Dagang, ZHAO Shuping, MENG Jie, et al. Modeling and flutter suppression of wind turbine blade constrained damping structure[J]. Journal of Solar Energy, 2018, 39(4): 1165-1172. (in Chinese) |
| [2] |
张志超, 黄微波, 李华阳, 等. 黏弹性阻尼材料及其阻尼结构的研究进展[J]. 环保科技, 2017, 23(6): 56-60.
ZHANG Zhichao, HUANG Weibo, LI Huayang, et al. Research progress of viscoelastic damping materials and structures[J]. Environmental Protection Technology, 2017, 23(6): 56-60. (in Chinese) DOI:10.3969/j.issn.1674-0254.2017.06.013 |
| [3] | KERWIN E M. Damping of flexural waves by a constrained viscoelastic layer[J]. Journal of the Acoustical Society of America, 1959, 31(7): 952-962. DOI:10.1121/1.1907821 |
| [4] |
王金朝, 王志强, 徐宁, 等. 约束阻尼板结构模态实验及阻尼特性研究[J]. 噪声与振动控制, 2018, 38(6): 205-208.
WANG Jinchao, WANG Zhiqiang, XU Ning, et al. Modal experiment and damping characteristics of constrained damping plate structure[J]. Noise and Vibration Control, 2018, 38(6): 205-208. (in Chinese) DOI:10.3969/j.issn.1006-1355.2018.06.039 |
| [5] |
陈威, 夏利娟. 黏弹性自由阻尼加筋板的随机响应分析和试验研究[J]. 舰船科学技术, 2020, 42(1): 62-67.
CHEN Wei, XIA Lijuan. Random response analysis and experimental study of viscoelastic free damping stiffened plates[J]. Ship Science and Technology, 2020, 42(1): 62-67. (in Chinese) DOI:10.3404/j.issn.1672-7649.2020.01.013 |
| [6] |
黄微波, 张志超, 李华阳, 等. 层间厚度对约束阻尼结构振动性能的影响[J]. 工程抗震与加固改造, 2018, 40(1): 8-14.
HUANG Weibo, ZHANG Zhichao, LI Huayang, et al. Effect of interlayer thickness on vibration performance of constrained damping structures[J]. Earthquake Resistance and Reinforcement, 2018, 40(1): 8-14. (in Chinese) |
| [7] | JIN G, Yang C, LIU Z. Vibration and damping analysis of sandwich viscoelastic-core beam using Reddy's higher-order theory[J]. Composite Structures, 2016, 140: 390-409. DOI:10.1016/j.compstruct.2016.01.017 |
| [8] | MOKHTARI M, PERMOON M R, HADDADPOUR H. Dynamic analysis of isotropic sandwich cylindrical shell with fractional viscoelastic core using Rayleigh-Ritz method[J]. Composite Structures, 2018, 186: 165-174. DOI:10.1016/j.compstruct.2017.10.039 |
| [9] | YANG X D, YU T J, ZHANG W, et al. Damping effect on supersonic panel flutter of composite plate with viscoelastic mid-layer[J]. Composite Structures, 2016, 137: 105-113. DOI:10.1016/j.compstruct.2015.11.020 |
| [10] | HUANG Z C, QIN Z Y, CHU F L. Damping mechanism of elastic-viscoelastic-elastic sandwich structures[J]. Composite Structures, 2016, 153: 96-107. DOI:10.1016/j.compstruct.2016.05.105 |
| [11] | EBRAHIMI F, BARATI M R. Damping vibration analysis of smart piezoelectric polymeric nanoplates on viscoelastic substrate based on nonlocal strain gradient theory[J]. Smart Materials and Structures, 2017, 26: 065018. DOI:10.1088/1361-665X/aa6eec |
| [12] | ZHANG S Q, SCHMIDT R. Static and dynamic FE analysis of piezoelectric integrated thin-walled composite structures with large rotations[J]. Composite Structures, 2014, 112: 345-357. DOI:10.1016/j.compstruct.2014.02.029 |
| [13] | ZHANG S Q, SCHMIDT R. Large rotation theory for static analysis of composite and piezoelectric laminated thin-walled structures[J]. Thin-Walled Structures, 2014, 78: 16-25. DOI:10.1016/j.tws.2013.12.007 |
| [14] | MOITA J S, ARAÙJOA L, MARTINS P G, et al. Analysis of active-passive plate structures using a simple and efficient finite element model[J]. Mechanics of Advanced Materials and Structures, 2011, 18(2): 159-169. DOI:10.1080/15376494.2010.496062 |
| [15] | BILASSE M, OGUAMANAM D C D. Forced harmonic response of sandwich plates with viscoelastic core using reduced-order model[J]. Composite Structures, 2013, 105: 311-318. DOI:10.1016/j.compstruct.2013.05.042 |
2. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200072, China;
3. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China




