2. 兰州理工大学 机电学院, 甘肃 兰州 730050
生产过程中对异常因素的识别和诊断是维持过程稳定、安全运行的重要环节。过程监控方法目前已从生产制造领域发展到服务、医疗和交通等领域, 对过程中的异常防微杜渐, 能够有效避免大的质量和安全问题。近年, 随着传感技术和计算机技术的发展, 对复杂过程安全性、可靠性和高效性能的监控提出了更高的要求。例如, 在缺陷检测方面, 具有多种质量特性的工业产品中经常出现不同类型的缺陷, 这些缺陷之间有可能相互作用[1]; 在医疗领域, 某一时间段内, 相邻区域感染某种疾病的人数存在相关性[2]。
控制图是统计过程控制领域的一种重要工具。通过对过程数据的采集、分析、计算和打点, 实时监控过程的运行状况, 并对过程异常及时报警, 从而达到监控的目的。根据过程数据的维度, 其分为单值控制图和多元控制图。常见的单值控制图有适用于监控连续变量的休哈特图(Shewhart chart)、EWMA (exponentially weighted moving average)图和CUSUM (cumulative sum)图; 监控一元离散变量的有c图、u图等。这些控制图应用范围很广, 但是其假设观测值是独立同分布的, 直接将其运用到多元情形会忽略数据间的关联性。为此,多元控制图应运而生, 主要包括用于监控离散变量的np图、D图[3],用于监控连续变量的多元Shewhart图(T2图)、多元EWMA图[4]和多元CUSUM图。其中, np图和D图将多元离散数据转化成一元数据, 忽视了多元数据的相关性; 多元Shewhart图(T2图)、多元EWMA图和多元CUSUM图不但研究了多个变量, 并且同时考虑了变量之间的相关性, 但这些控制图假设变量服从正态分布。综上所述, 这些控制图在多元离散过程监控中有局限性。
因此有必要建立一种针对多元离散型过程数据的控制图。最初, Niaki和Abbasi[5]考虑把多元Poisson分布转化为近似的多元正态分布进而采用T2控制图监控。但当数据的均值较小或者存在很多零值时, 这种近似会产生较大误差。Chen等[6]假设Poisson过程的参数服从多元对数正态分布, 并构建多元EWMA控制图监控多元Poisson过程, 但这一模型忽视了不同维度数据间的空间关联性, 在应用中有一定的局限性。He和龙威等[7-8]分别在等方差和异方差多元Poisson模型基础上, 构建了CUSUM控制图。这类模型的相关性度量不够灵活, 不适应如非线性或对称性的关联结构。
由于copula模型在处理非线性、非正态等结构上的优势, 在金融和经济领域得到广泛应用。与此同时, 这一方法也被引入到多元数据建模和监控领域。Dokouhaki等[9]基于copula函数构建面向二元自相关二项型数据的CUSUM控制图。Sasiwan-napong等[10]假设观测值服从指数分布, 应用多种copula构建T2和多元EWMA控制图。Sukparungsee等[11]采用5种copula(Normal, Clayton, Frank, Gum-bel, Joe copula)构建T2控制图用于监控指数型特征值。Kuvattana等[12]针对二元指数型数据构建了多元EWMA和多元CUSUM控制图, 仿真结果显示多元EWMA控制图的监控效果最好, 并且基于Normal copula构建的多元EWMA图可以用于监控正负相关及各种强度相关性下的漂移。针对多零值离散数据, Fatahi等[13]应用零膨胀Poisson分布(zero inflated Poisson distributions)构建基于copula的联合概率分布监控二元稀少事件(rare event)。考虑到非正态变量, Krupskii等[14]构建了对密度函数形状变化敏感的多元过程监测方案。Chen[15]采用Normal copula描述时间序列的自相关和多元数据的互相关, 并实施了多元EWMA控制图。近期, Song等[16]提出基于copula的非参数方案, 监控二元未知分布的位置和规模信息。综上所述, 多数研究聚焦于二元或连续型数据建模及监控。这主要有两方面原因:①把二元copula函数推广到多元情形会产生较复杂的结构, 也给参数估计带来困难;②离散边缘分布往往会产生不唯一的copula函数。因此, 有必要探索针对三元离散数据的建模和控制图研究。
本文以三元Poisson过程数据为对象, 考虑各时刻不同维度数据的空间相关性, 引入三元Clayton copula描述各维度数据的相关性, 根据对数似然比检验理论, 设计出与模型匹配的控制图。采用马尔科夫链法近似求解出多种参数变化下的平均运行链长, 最终验证控制图的监控性能。
1 Clayton copula简介 1.1 copula函数简介copula模型广泛应用于描述和度量变量间的非线性的相关结构[17]。以常见的二元copula函数为例, 二元变量(y1, y2)的边缘分布函数和联合分布函数为F1, F2和F。简便起见, 记v1=F1(y1), v2=F2(y2),且v1∈[0, 1], v2∈[0, 1], copula函数记做C(v1, v2), 存在如(1)式所示关系
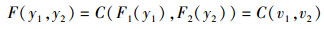
|
(1) |
式中,C(v1, v2)∈[0, 1], 且满足以下性质:
1) 对于所有的v1, v2∈[0, 1], 存在
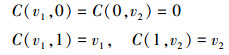
|
2) 对于所有的v1, v2, v′1, v′2 ∈[0, 1], 如果v′1≥v1, v′2≥v2, 则
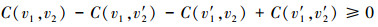
|
如果边缘分布函数F1, F2均连续, 那么copula函数是唯一的, 反之, copula函数往往不唯一。限于此, copula函数目前在连续型过程得到充分应用, 而在离散和混合过程应用较少。
根据构造原则常常把copula分为阿基米德族和椭圆族。阿基米德函数族copula结构类似, 根据生成函数的不同将其分为Clayton, Frank和Gumbel函数等。而椭圆族copula是由椭圆族函数推导而来, 常见的有Gaussian和Student-t等。又根据参数的数量分为单一参数copula和多参数copula。各种类型的copula在描述相关性时有所差别[18]。Gaussian copula可以灵活地描述同等程度的正相关和负相关, 并在其允许范围内包含Fréchet边界[18]。Clayton copula不适用于解释负相关关系, 但适用于高强度的正向相关。Frank copula在实践中得到广泛应用, 因为Fréchet边界包含在其允许范围内。
1.2 Clayton copula模型Clayton copula是阿基米德函数族中常见的单一参数模型[17], 广泛应用于金融和经济领域。二元Clayton copula定义为
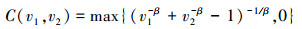
|
(2) |
式中,β∈(-1, +∞)\{0}。Clayton copula是常见的单变量copula模型, 生成函数为
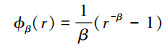
|
满足ϕ(C(v1, v2))=ϕ(v1)+ϕ(v2)性质。
三元Clayton copula [19]定义为

|
(3) |
式中, β>0是唯一参数, 表示任意2种变量(v1和v2; v1和v3; v2和v3)的相关性。该模型有很强的对称性并且结构简单, 适用于三元数据建模。
2 基于copula的三元Poisson模型实际生产过程中, 多种质量特性在同一时刻的采样值往往存在相关信息。某一时刻t采集到M个离散的观测值, 记做Yt=(Yt, 1, …, Yt, M)。假设Yt服从多元Poisson过程, 不同时刻采集的数据间相互独立(如Yt, Yt-1), 且每个时刻的观测值存在空间相关性(如Yt, 1, Yt, 2)。考虑Yt的空间相关性, 用copula来构建其联合概率质量函数。假设对所有t=1, …, T, 向量Yt=(Yt, 1, …, Yt, M)的联合分布为
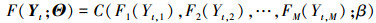
|
(4) |
式中:β代表copula参数;Fi代表边缘累积分布函数, i=1, …, M。
对于二元Poisson过程, 在时刻t获得的2个观测值可以表达为向量Yt=(Yt, 1, Yt, 2), 其联合分布和概率质量函数分别表示为
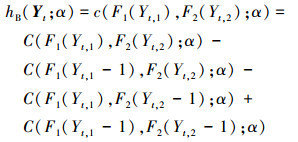
|
(5) |
同理, 三元Poisson过程中变量Yt=(Yt, 1, Yt, 2, Yt, 3)的联合分布和概率质量函数分别表示为
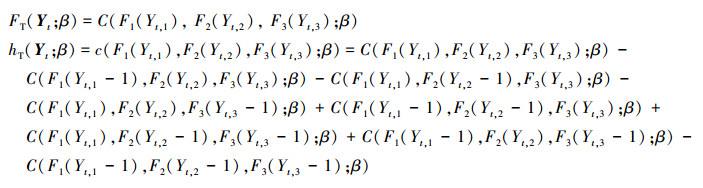
|
(6) |
三元Poisson过程的协方差矩阵表示为
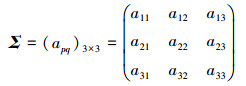
|
(7) |
式中,apq=aqp且apq=cov(Y*, p, Y*, q), p, q=1, 2, 3。根据协方差的定义结合copula理论可以计算
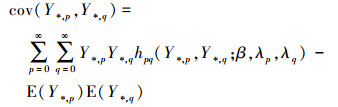
|
式中,E(Y*, p)是Y*, p边缘分布的均值, (Y*, p, Y*, q)的二元联合概率质量函数为
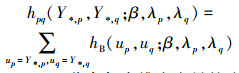
|
显然, 对于Poisson分布每个维度变量的取值范围是非负整数集。由于各变量的协方差不恒定, 本模型也属于异方差模型。
实践中, 分布参数λ及copula参数β往往是未知的, 需要根据一系列稳态观测值估计这些参数。两阶段最大似然估计法, 也称作IFM(inference functions for margins)方法[20], 是一种常用的多元copula模型的参数估计方法, 表述如下:
第一阶段是边缘分布的参数估计, 采用极大似然估计法分别求解各边缘分布li(Yi; λi)的对应参数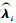
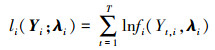
|
(8) |
第二阶段是copula参数估计。在估计得出的边缘分布参数条件下, 采用极大似然估计法求解其联合似然函数
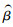
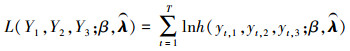
|
(9) |
两阶段估计法在连续情形效果显著, 并得到了广泛应用。而在离散情形下, 估计参数在小维度情形很有效, 对于大维度数据的效果次之[20]。
3 三元CUSUM控制图设计针对多变量监控问题, 联合监控多个变量比单独监控一个变量更加容易发现过程异常[19]。考虑到空间相关性建模并获得适用的受控模型及参数后, 需要结合数据特点及控制图原理设计出适用的控制图。本文结合第2节的三元相关Poisson数据模型, 设计多元CUSUM控制图。假设同一时刻的三元Poisson数据存在空间相关, 而不同时刻的数据间相互独立。记t时刻的三元Poisson数据为Yt=(Yt, 1, Yt, 2, Yt, 3), t=1, …, T, 各个维度的参数记做λ=(λ1, λ2, λ3)。假设受控状态的Poisson参数为λ0,偏移发生后变化为λc,变点模型可表示为
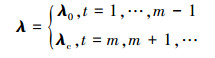
|
根据似然比检验的思想, 对变点存在和不存在2种情形的联合密度函数做似然比, 构造统计量
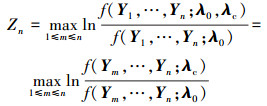
|
(10) |
式中, f(Ym, …, Yn; λ0)和f(Ym, …, Yn; λc)是(Ym, …, Yn)分别在λ=λ0和λ=λc时的联合密度函数。记
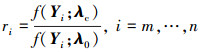
|
(11) |
式中,f(Yi)是概率质量函数。对于本文所讨论的二元Poisson过程, f(Yi)=hB(yi, 1, yi, 2); 同理, 三元过程中, f(Yi)=hT(yi, 1, yi, 2, yi, 3)。基于此, 似然比统计量可以进一步写做
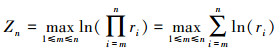
|
(12) |
等价的递归形式可表示为
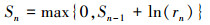
|
(13) |
式中,S0=0。一旦Sn超出给定的控制限h则会报警, 意味着存在变点m, 即Poisson参数λ发生了改变; 否则, 认为过程参数λ没有显著改变, 即过程处于受控状态。
4 仿真实验与分析 4.1 多元相关Poisson数据的生成基于copula模型生成多元数据是建立在条件分布基础上的。由于copula模型的多样性, 数据生成存在一定差异。本节以三元Poisson过程为例, 生成基于Clayton copula的随机数据。记变量v1和(v1, v2)的条件概率密度函数分别为C1(v1)和C1(v1, v2), 存在

|
另记Ck(vk; v1, …, vk-1)为条件分布, 即给定(v1, …, vk-1)条件下vk的条件分布。对三元变量问题, k=1, 2, 3。若分子分母同时存在且分母不为零时

|
(14) |
当k=1时显然存在C1(v1)=v1, 当k=2, 3时可以推算出
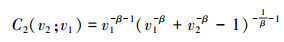
|
(15) |
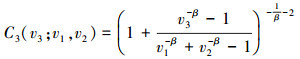
|
(16) |
生成一组三元Poisson数据的过程如下所示:
1) 从均匀分布U(0, 1)中随机生成v1;
2) 从均匀分布U(0, 1)生成随机数作为C2(v2; v1)的实际值, 结合v1求解方程得v2;
3) 从均匀分布U(0, 1)生成随机数作为C3(v3; v1, v2)的实际值, 结合v1和v2求解方程得v3;
4) 应用Poisson分布的反函数得到一组数据(y1, y2, y3), 其中, y1=F-1(vi), i=1, 2, 3。
4.2 参数估计设定Poisson过程的3个参数λ=(λ1, λ2, λ3), 以及描述空间关联的copula参数β。本研究采用Clayton copula参数β=1, 3, 5表达3种不同强度的相关性。控制图实施过程中这些参数往往是未知的, 因此采用两阶段估计法估计稳态过程参数。具体步骤为:①根据4.1节介绍的方法生成100 000个三元Poisson数据;②在阶段一采用极大似然估计法分别估计3个维度的分布参数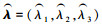
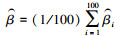
目前, 主流的用于评价控制图监控效果的指标是平均运行链长(average run length, ARL), 即运行链长(RL)的期望值。而运行链长RL是指从开始到第一次失控报警的样本点数目。本文采用马尔科夫链(Markov chain)近似计算多元CUSUM控制图平均运行链长。控制限记做h, 受控的多元Poisson参数为λ0=(λ1, λ2, λ3), 目标参数记做λc=θλ0, 失控参数λd=(δ1λ1, δ2λ2, δ3λ3)。首先将受控区间分为ne等分, 每一段的长度Δ=h/ne, 每部分区间可表示为[(k-1)Δ, kΔ), k=1, 2, …, ne。一旦统计量落入区间k, 认为统计量近似取区间中点值, 即(k-0.5)Δ。假定转移矩阵P中的每一个元素pjk代表统计量从区间j转移到区间k的概率, 记做
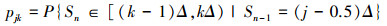
|
(17) |
式中,j, k=1, 2, …, ne。转移概率的计算首先需要列举出所有可能的三元Poisson数据组合, 并分别计算其联合概率。需要注意的是, 计算受控ARL(L0)时, 采用hT(Yt; λ0, β); 反之, 计算失控ARL(L1)时, 采用hT(Yt; λd, β)计算。对转移矩阵做一些变换即可得到表示ARL的向量L
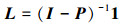
|
(18) |
式中, I是单位矩阵, 1是全为1的列向量。由于初始值S0=0, 因此向量L的第一个元素即为ARL的近似值。值得注意的是, 该方法近似计算ARL的精确程度受到间隔的等分数ne影响。ne越大, 计算的ARL越接近真实值, 但是计算时间会相应增加。
4.4 三元CUSUM控制图的监控效果在缺陷监测和疾病预防的背景下, 本文关注多元Poisson数据的异常增长, 采用单侧向上的控制图考察监控效果。同理, 单侧向下或双侧控制图可以根据实际情况选择。鉴于多元Poisson数据的特点, 控制图的控制下限不做要求, 控制上限记做h。在阶段一, 给定适当的受控ARL, 采用马尔科夫链的方法搜索控制限h。
对三元Poisson过程的每个维度分别考虑3种异常参数, 则会有33=27种组合。显然, 实现每一种组合的异常参数集合是不现实的。因此, 考虑了9种组合方式。每一种组合方式中, 参数变化幅度可记为δ=(δ1, δ2, δ3), 又因为受控参数λ0=(λ1, λ2, λ3), 则异常参数λd=(δ1λ1, δ2λ2, δ3λ3)。此外, 控制图设计中的目标参数λc=(θλ1, θλ2, θλ3)。考虑到设计过程的便利性, 设定为1.1, 1.5和2.0。
设定λ0=(10, 10, 10)且L0=200, 表 1和表 2分别展示了3种copula 参数和3种目标参数条件下的控制限和失控平均运行链长。其中, 序号1~3仅有1个维度的参数发生向上阶跃, 4~6有2个维度发生变化, 7~9表示3个维度均发生变化的情形。文献[4, 7]采用一种表征马氏距离的变化尺度(shift size)量, 或称为非中心性参数(non-centrality para-meter)
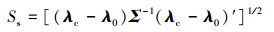
|
| β | θ | h |
| 1 | 1.1 1.5 2.0 |
2.50 3.30 2.05 |
| 3 | 1.1 1.5 2.0 |
2.49 3.32 2.44 |
| 5 | 1.1 1.5 2.0 |
2.55 3.43 2.57 |
| 序号 | δ1 | δ2 | δ3 | β=1 | β=3 | β=5 | ||||||||
| θ=1.1 | θ=1.5 | θ=2.0 | θ=1.1 | θ=1.5 | θ=2.0 | θ=1.1 | θ=1.5 | θ=2.0 | ||||||
| 1 | 1.1 | 1 | 1 | 77.74 | 105.54 | 117.86 | 108.15 | 116.05 | 142.25 | 156.14 | 132.64 | 174.21 | ||
| 2 | 1 | 1.5 | 1 | 14.63 | 18.41 | 27.05 | 52.32 | 40.49 | 82.98 | 134.53 | 70.41 | 154.25 | ||
| 3 | 1 | 1 | 2.0 | 5.74 | 5.13 | 7.70 | 13.96 | 12.59 | 33.07 | 29.67 | 24.10 | 95.06 | ||
| 4 | 1.1 | 1.1 | 1 | 38.01 | 58.38 | 70.11 | 51.59 | 64.53 | 86.88 | 71.31 | 73.76 | 96.43 | ||
| 5 | 1 | 1.5 | 1.5 | 5.83 | 5.38 | 7.18 | 14.05 | 11.23 | 19.23 | 27.54 | 18.56 | 33.75 | ||
| 6 | 2.0 | 1 | 2.0 | 2.67 | 2.12 | 2.68 | 4.97 | 4.85 | 10.43 | 7.71 | 8.43 | 24.27 | ||
| 7 | 1.1 | 1.1 | 1.1 | 21.93 | 33.64 | 42.58 | 22.95 | 34.79 | 51.84 | 22.64 | 36.55 | 57.30 | ||
| 8 | 1.5 | 1.5 | 1.5 | 3.04 | 2.24 | 2.38 | 3.27 | 2.47 | 2.89 | 3.38 | 2.52 | 3.07 | ||
| 9 | 2.0 | 2.0 | 2.0 | 1.48 | 1.16 | 1.14 | 1.55 | 1.24 | 1.21 | 1.62 | 1.28 | 1.21 | ||
式中, λ0和λc分别是受控和失控的参数向量。如公式(7)所示, Σ是协方差矩阵。非中心性参数能够度量过程参数的整体变化。对于2组异常参数, 如果其非中心性参数相等, 则L1也相当。例如, 表 2中序号1代表的异常参数的变化幅度为δ=(1.1, 1, 1), 其性能与δ=(1, 1.1, 1)及δ=(1, 1, 1.1)情形相当。同理, 序号6代表的异常参数的变化幅度为δ=(2, 1, 2), 其性能与δ=(2, 2, 1)及δ=(1, 2, 2)情形相当。因此, 表 2所列出的9种组合方式足够代表全部27种异常情形的ARL性能。从表 2中可以看出, 当参数有变化时, L1值均小于L0值, 即L0=200, 说明本文方法可以检测多元Poisson过程均值向上偏移。并且, 随着参数变化的幅度值不断增大, L1越来越小。对于一种特定的失控状态, 随着copula参数的增加, 平均运行链长普遍增大。也就是说, 多元过程的空间相关性越来越强时, 监控异常变化的难度也越来越大。对比3种目标幅度值来看, θ=1.1的控制图对δ1=δ2=δ3=1.1(序号7)的异常情况效果好; θ=1.5的控制图对δ1=δ2=δ3=1.5(序号8)效果好; θ=2的控制图对δ1=δ2=δ3=2(序号9)效果好。因此, 设计多元Poisson控制图时, 对较小的变化幅度需要选择较小的θ, 反之, 对于可能存在的较大变化, 选择较大的θ可获得更理想的效果。
图 1展示了Poisson数据及其在多元CUSUM控制图的应用。设定异常参数的变化幅度δ=(1.1, 1.1, 1.1), 则目标参数的变化幅度选为θ=δ。三元Poisson数据由4.1节方法生成。图 1a)~1c)分别代表β=1, 3, 5时对应的多元Poisson数据, 而对应的CUSUM统计量绘制在图 1d)~1f)中。每组Poisson数据包括3个维度, 每个维度有20个受控数据和20个失控数据, 图中用蓝色虚线分隔。红色水平线代表在L0=200水平下的控制限。从表 1中可得出在β分别取1, 3, 5时对应的控制限为2.5, 2.49和2.55。从图 1中可以看出, 对于所列出的3种β取值, 提出的方法对失控数据都有较好的检出力。
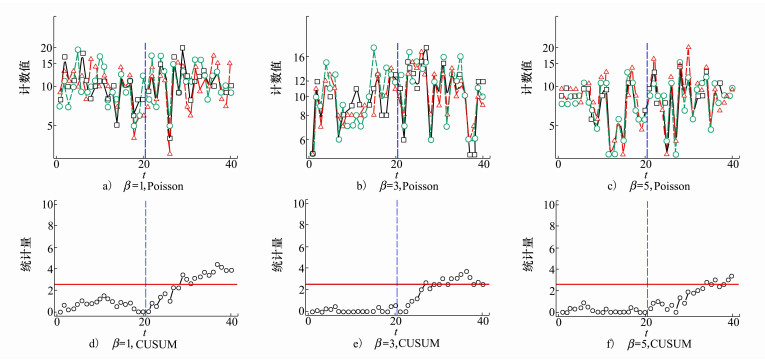
|
| 图 1 Poisson过程数据及其在CUSUM控制图的应用(L0=200) |
图 2对比了本文所提方法与文献[3]中D图的性能。为了便于对比, 实验假定δ=δ1=δ2=δ3, 其中δ=1代表受控状态, δ=1.1, 1.2, …, 2代表失控状态。图 2a)~2c)分别展示在β=1, 3, 5条件下D图和本文所提多元CUSUM控制图在θ=1.1, 1.5的ARL对比。从图中可以看出, D图在β=1条件下监控较大偏移量(θ≥1.2)性能优于本文所提CUSUM控制图。当β=3, 5时, 本文提出的CUSUM控制图对所有偏移量均取得更小的L1。其中θ=1.1的CUSUM控制图对较小的偏移量监测效果最好, θ=1.5的CUSUM控制图对较大的偏移量监测效果最好。这一点与表 2的结论一致。
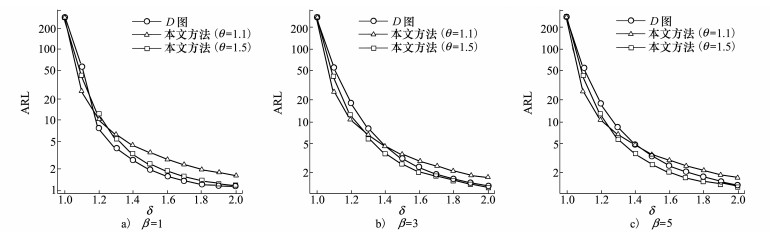
|
| 图 2 D图与本文提出CUSUM控制图的性能对比 |
针对具有空间对称相关结构的三元Poisson过程监控问题, 首先采用三元Clayton copula函数描述其相关性, 并构建联合分布; 在假设copula参数不变的前提下, 基于对数似然比检验方法结合联合分布信息, 推导出多元CUSUM控制图的监控统计量; 在给定初始值的前提下, 利用马尔科夫链方法近似求解ARL, 验证其有效性, 并与D图做对比。仿真结果表明, 提出的方法能够有效监测过程均值的向上漂移, 并且目标偏移量与实际偏移量相等时可以获得更好的监控性能。与D图相比, 当数据间的相关性较强时, 提出的方法对于所有的偏移量能取得更好监控效果。在未来工作中, 将进一步研究时间和空间关联同时存在的多元数据建模及监控问题。
| [1] | LI C I, PAN J N, HUANG M H. A new demerit control chart for monitoring the quality of multivariate Poisson processes[J]. Journal of Applied Statistics, 2019, 46(4): 680-699. DOI:10.1080/02664763.2018.1510477 |
| [2] | PASCUAL F G, AKHUNDJANOV S B. Copula-based control charts for monitoring multivariate Poisson processes with applica-tion to hepatitis C counts[J]. Journal of Quality Technology, 2020, 52(2): 128-144. DOI:10.1080/00224065.2019.1571337 |
| [3] | CHIU J E, KUO T I. Attribute control chart for multivariate Poisson distribution[J]. Communications in Statistics-Theory and Methods, 2007, 37(1): 146-158. DOI:10.1080/03610920701648771 |
| [4] | LOWRY C A, WOODALL W H, CHAMP C W, et al. A multivariate exponentially weighted moving average control chart[J]. Technometrics, 1992, 34(1): 46. DOI:10.2307/1269551 |
| [5] | NIAKI S T A, ABBASI B. Monitoring multi-attribute processes based on norta inverse transformed vectors[J]. Communications in Statistics-Theory and Methods, 2009, 38(7): 964-979. DOI:10.1080/03610920802346119 |
| [6] | CHEN N, LI Z, OU Y. Multivariate exponentially weighted moving-average chart for monitoring Poisson observations[J]. Journal of Quality Technology, 2015, 47(3): 252-263. DOI:10.1080/00224065.2015.11918131 |
| [7] | HE S, HE Z, WANG G A. CUSUM control charts for multivariate Poisson distribution[J]. Communications in Statistics-Theory and Methods, 2014, 43(6): 1192-1208. DOI:10.1080/03610926.2012.667484 |
| [8] |
龙威, 李艳婷. 基于多元泊松模型的累积和控制图设计[J]. 应用概率统计, 2020(3): 221-237.
LONG Wei, LI Yanting. CUSUM control chart design for multivariate Poisson distribution[J]. Chinese Journal of Applied Probability and Statistics, 2020(3): 221-237. (in Chinese) DOI:10.3969/j.issn.1001-4268.2020.03.001 |
| [9] | DOKOUHAKI P, NOOROSSANA R. A copula Markov CUSUM chart for monitoring the bivariate auto-correlated binary observations[J]. Quality and Reliability Engineering International, 2013, 29(6): 911-919. DOI:10.1002/qre.1450 |
| [10] | SASIWANNAPONG S, SUKPARUNGSEE S, BUSABABODHIN P, et al. The efficiency of constructed bivariate copulas for MEWMA and hotelling's T2 control charts[J]. Communications in Statistics-Simulation and Computation, 2022, 51(4): 1837-1851. DOI:10.1080/03610918.2019.1687719 |
| [11] | SUKPARUNGSEE S, KUVATTANA S, BUSABABODHIN P, et al. Bivariate copulas on the hotelling's T2 control chart[J]. Communications in Statistics-Simulation and Computation, 2018, 47(2): 413-419. DOI:10.1080/03610918.2016.1228958 |
| [12] | KUVATTANA S, SUKPARUNGSEE S. Comparative the performance of control charts based on copulas[C]//World Congress on Engineering and Computer Science, 2017: 47-58 |
| [13] | FATAHI A A, NOOROSSANA R, DOKOUHAKI P, et al. Copula-based bivariate ZIP control chart for monitoring rare events[J]. Communications in Statistics-Theory and Methods, 2012, 41(15): 2699-2716. DOI:10.1080/03610926.2011.556296 |
| [14] | KRUPSKII P, HARROU F, HERING A S, et al. Copula-based monitoring schemes for non-Gaussian multivariate processes[J]. Journal of Quality Technology, 2020, 52(3): 219-234. DOI:10.1080/00224065.2019.1571339 |
| [15] | CHEN Y. EWMA control charts for multivariate autocorrelated processes[J]. Statistics and Its Interface, 2017, 10(4): 575-584. DOI:10.4310/SII.2017.v10.n4.a4 |
| [16] | SONG Z, MUKHERJEE A, ZHANG J. Some robust approaches based on copula for monitoring bivariate processes and component-wise assessment[J]. European Journal of Operational Research, 2021, 289(1): 177-196. DOI:10.1016/j.ejor.2020.07.016 |
| [17] | CLAYTON D G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence[J]. Biometrika, 1978, 65(1): 141-151. DOI:10.1093/biomet/65.1.141 |
| [18] | ZIMMER D M, TRIVEDI P K. Using trivariate copulas to model sample selection and treatment effects[J]. Journal of Business & Economic Statistics, 2006, 24(1): 63-76. |
| [19] | FERREIRA P H, LOUZADA F. Extending the inference function for augmented margins method to implement trivariate Clayton copula-based SUR tobit models[J]. Communications in Statistics-Theory and Methods, 2020, 49(6): 1375-1401. DOI:10.1080/03610926.2018.1563167 |
| [20] | JOE H. Asymptotic efficiency of the two-stage estimation method for copula-based models[J]. Journal of Multivariate Analysis, 2005, 94(2): 401-419. DOI:10.1016/j.jmva.2004.06.003 |
2. School of Mechanical Engineering, Lanzhou University of Technology, Lanzhou 730050, China




