直升机旋翼带来了垂直起降、低空悬停、高机动性等固定翼飞行器无法比拟的独特优势, 同时也导致了振动水平较大等问题, 使直升机振动控制成为科研和工程人员高度关注的课题[1-2]。国内外在长期的技术研究和工程实践中先后发展了节点粱隔振、聚焦式隔振、动力反共振隔振(DAVI)等振动控制方案, 装机实践取得了一定的减振效果。
传统的动力反共振系统由弹簧、阻尼杠杆和配重(惯性元件)等组成, 选择适当的设计参数, 惯性元件的运动可消除激振向下传递。20世纪80年代, Halwes基于动力反共振原理进一步提出了液弹隔振的理念[3]。液弹隔振其是在机械式DAVI隔振器的基础上, 用橡胶提供弹性刚度, 通过液体在惯性通道内的运动产生上下液腔压力变化抵消激振力。采用液体作为惯性元件, 具有更大的当量力臂, 有效地避免了机械式杠杆产生的磨损, 并且液弹隔振系统具有结构简单、质量轻、隔振频带宽等优点。
国内外研究人员对液弹隔振器进行大量的研究[3-9], 美国Lord公司生产的Fluidlastic液弹隔振器已经形成了完整产品线, 并已经成功应用在Bell公司的427, 429, 430型等多个型号的直升机上[3]。Mcgurie等[10]研究了适用于直升机短舱的高刚度“刚性”液弹隔振系统。Han等[11]设计了一种用于直升机主旋翼变距拉杆的隔振器模型, 用于减少高阶谐波载荷。对摆振柔软直升机进行旋翼-隔振器耦合气弹模拟, 仿真结果表明, 在大速度前飞下使用液弹隔振器可减少98%的4倍转速变距拉杆载荷, 其他阶次载荷变化较小。Sun等[12]建立了一种基于磁流变液的隔振器模型, 采用磁流变液控制隔振器刚度和阻尼,分析了隔振器的振幅依赖响应和频率依赖响应动特性, 试验结果表明了隔振器可调节刚度和阻尼。Leng等[13]提出了一种适用于磁流变液隔振器的模型, 模型中考虑了磁流变液的黏弹性、时滞性和摩擦效应, 以此研究磁流变液弹隔振器的能量耗散机制。论文研究了参数敏感性, 并将理论计算结果与试验值比较验证所提出模型的准确性。
龚亮[14]设计了一种液弹隔振器, 建立了动力学模型, 并制作原型, 惯性通道选择螺旋通道以减小隔振器长度。冯志壮等[15]设计了一种带斜角橡胶件的气新型主减液弹隔振器。通过动力学建模计算, 分析了液弹隔振器传递特性, 结果表明隔振器在各向减振效率高于60%的情况下仍具有较高的静刚度, 可适用于直升机工程应用。Cheng等[16-17]针对内简嵌入式液弹隔振器建立动力学模型, 开展隔振效果评估及参数影响分析, 结果表明液体密度、通道长度及放大比等因素对隔振器动特性有较强影响。钱峰等[18]设计一种液弹隔振器, 并开展试验研究, 标定了隔振器的动刚度、静刚度等参数, 分析不同设计参数对载荷传递率的影响。Deng等[19-20]针对液弹隔振器设计中涉及到的种类繁多的材料参数和可变系数, 采用正交试验法等方法创建二索引、六影响因素的正交试验表, 探究设计参数对动刚度等特性的影响强弱。
国外液弹隔振器已实现装机应用, 国内以理论分析为主。本文基于动力反共振原理构建组合式液弹隔振器动力学模型, 针对某民机机型振动特性设计液弹隔振器主要参数, 制作原理样件并进行试验验证, 考察隔振器在不同激励频率及激励位移幅值下的隔振特性, 并与理论模型比较, 验证模型的准确性。
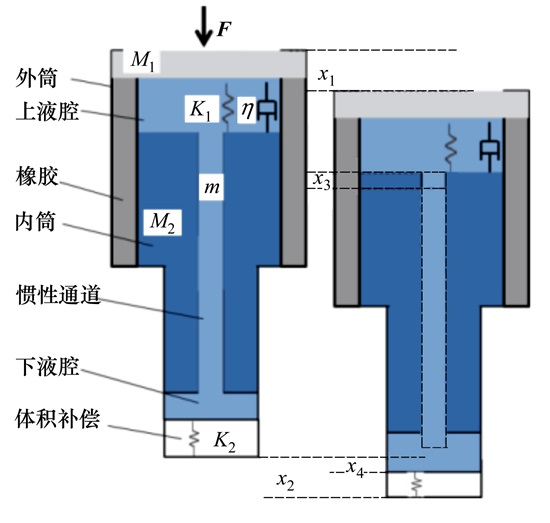
1 理论建模组合式液弹隔振器简化模型如图 1所示, 其原理与传统机械式动力反共振相同, 动力反共振隔振系统的弹簧由内外筒之间的橡胶取代, 惯性通道内的流动液体作为惯性元件, 上、下液腔与惯性通道的面积比即为动力反共振中杠杆的放大比。当隔振器受到外加简谐激励的作用, 惯性通道的液体因受力而来回振荡, 如果激振频率与隔振系统固有频率接近, 则产生共振, 隔振器下端位移信号放大; 反之当处于反共振频率点附近时, 外界输入的能量转化成为通道内液体的动能, 从而使隔振器下端的响应大幅度降低, 如不考虑阻尼, 则可达到理想中的完全隔振, 即下端响应位移为零。
|
| 图 1 反共振系统的力学模型 |
如图 1所示, 液弹隔振器外筒及其连接质量为M1, 内筒及其连接质量M2, 惯性通道内液体质量为m; 隔振器上液腔、下液腔及通道面积分别为Au, Ad和A0; 橡胶弹性刚度和隔振器下端刚度分别为K1、K2, 橡胶损耗因子和液体黏性阻尼为η和c。隔振器上端质量M1受外部简谐激励F作用, 其幅值为f, 频率为ω; 隔振器上端和下端的位移分别为x1、x2(以向下为正), 通道内液体相对通道位移为x3, 下液腔液体相对于内筒位移为x4。
系统的总动能为
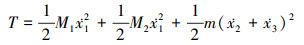
|
(1) |
类似地, 系统的弹性势能写为
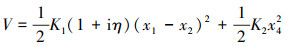
|
(2) |
耗散能为
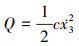
|
(3) |
由广义Lagrange原理推导系统控制方程
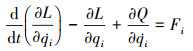
|
(4) |
式中,L=T-V, qi为广义坐标(i=1, 2), Fi为单个研究对象所受外力。同时由质量守恒可知,通过惯性通道截面液体与上、下液腔位移存在如下关系
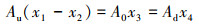
|
(5) |
记Au/A0=R1, Ad/A0=R2, 可得
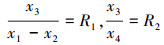
|
(6) |
将公式(6)代入公式(1)~(3)消去x3, x4简化变量代入方程(4)可得系统控制方程
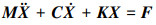
|
(7) |
式中
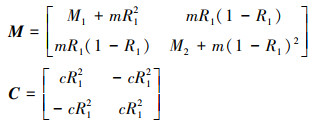
|
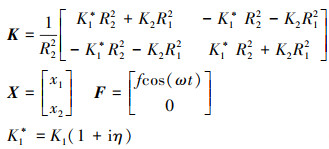
|
(8) |
由此可得液弹隔振器的位移传递率为
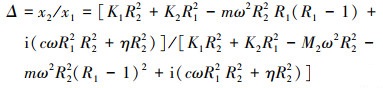
|
(9) |
在理想状态下不考虑阻尼(即c=0, η=0)可由公式(9)位移传递率为零得出理想隔振频率

|
(10) |
直升机主要振动来源于由桨毂传下来的旋翼振动载荷, 其频率成分为kNΩ(k=1, 2, 3, …), N为桨叶片数, Ω为旋翼转速, 其中又以一阶(NΩ)为主导。由公式(10)可知设液弹隔振器的隔振频率与K1, K2, m, R1和R2等参数相关。参数分解可知, 橡胶刚度和下端弹簧刚度、液体密度、惯性通道长度和半径、上液腔和下液腔半径等均会影响液弹隔振器隔振频率。同时联合公式(9)~(10)可知橡胶损耗因子和液体黏性阻尼等同样对最终隔振频率和隔振效率(位移传递率)有影响[11, 14]。
通过选取上述隔振器K1, K2, m, R1和R2等5种设计参数, 研究了隔振器传递特性随参数变化的影响性。
由图 2~3可知, 放大比R1,R2会改变液弹隔振器最佳隔振频率,同时随着R1,R2的增加,最佳隔振频率也随之增加,R1,R2对传递特性曲线的形状没有影响,但在其他外部条件相同时(外激励及其他参数),存在一个最佳R1,R2值使得传递率最小(隔振效率最好)。
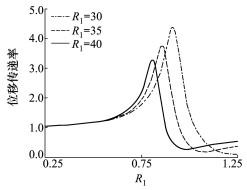
|
| 图 2 传递特性随R1变化 |

|
| 图 3 传递特性随R2变化 |
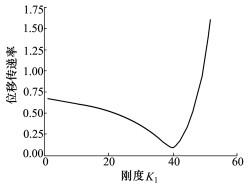
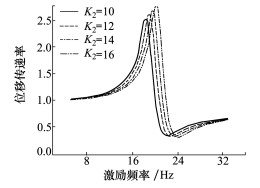
由图 4~5可以看出, 传递特性随不同K1, K2的变化规律相似, 但隔振频率点存在差异, 最佳隔振频率随K1, K2的增大而增大; 调节弹簧刚度K2可精确控制隔振频率; 在NΩ左右较宽的范围内, 不同的K1, K2下传递率计算值均小于0.1, 验证了液弹隔振器具有宽频带的减振效果。
|
| 图 4 传递特性随K1变化 |
|
| 图 5 传递特性随K2变化 |
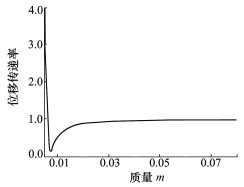
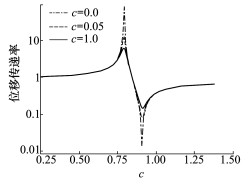
由图 6可知液弹隔振器隔振频率随通道液体质量增加而增加, 当激振频率不在液弹隔振器隔振频率时, 传递率会随之增加。液弹隔振器在隔振频率下能吸收最多的能量。由图 7可看出, 随着阻尼的增大, 隔振频率点的传递曲线数值增加且更为平缓, 传递率增加意味着隔振效率降低, 在设计时应选用低黏度的液体来获得较好的传递率。
|
| 图 6 传递特性随m变化 |
|
| 图 7 传递特性随c变化 |
针对某民用直升机, 考察其主减平台结构, 根据公式(9)~(10)并结合上述分析, 完成了图 1所示组合式液弹隔振器的参数设计, 其主要参数如表 1所示。
| 参数 | 设计值 | 参数 | 设计值 | |
| 上液腔半径 | 0.084 | 橡胶弹性刚度K1 | 35 | |
| 下液腔半径 | 0.041 | 下端刚度K2 | 1.27 | |
| 惯性通道长度 | 0.5 | 通道内液体质量m | 0.005 | |
| 液体黏度系数 | 0.003 1 |
通过前述综合分析, 采用上述设计的液弹隔振器, 在该型直升机NΩ激振频率处, 隔振器能发挥出最大隔振效果(位移传递率最小)。
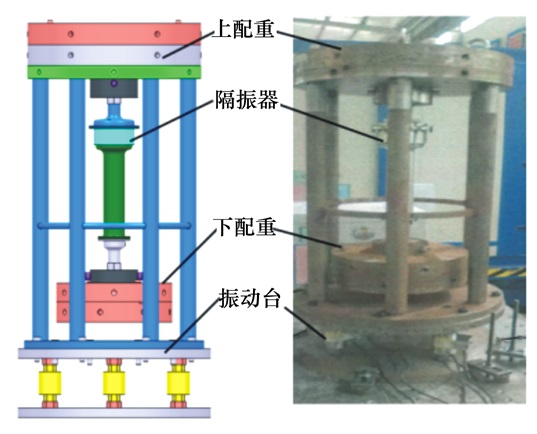
3 试验及结果以位移传递率为指标, 考察所设计的液弹隔振器的隔振效率, 据此设计如图 8所示的试验方案。隔振器上腔体(外筒)与刚性外支架固定, 下腔体(内筒)安装配重质量块M2, 模拟直升机部件。刚性支架底座与振动台台架之间固定, 振动台架的激振位移通过外支架传给上配重, 作用在隔振器上。在上配重和下配重上分别布置位移传感器, 实时记录隔振器上下两端位移。
|
| 图 8 液弹隔振器试验示意图与实物 |
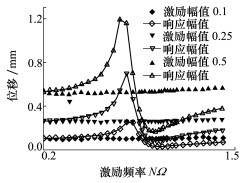
在垂直方向上施加简谐激振, 激振频率从0.2NΩ增加到1.375NΩ, 步长0.04NΩ, 其中在(0.83~1.08)NΩ范围内步长缩小到0.02NΩ, 提高精度。每个频率点进行定位移正弦激励, 位移幅值分别设为0.1, 0.25和0.5 mm, 考查隔振器在不同激励位移幅值下的隔振效果。试验时待每个频率点运动稳定后记录上端和下端数据, 每个频率和幅值重复3次, 最后试验结果取平均值, 结果如图 9所示。从图 9可知, 当激励频率远离共振点和反共振点时, 如激励频率小于0.42NΩ或大于1.25NΩ, 此时隔振器上下两端响应接近, 隔振器近似于刚性连接; 当激励频率接近共振点时, 下端的位移急剧增大; 而在预先设计的反共振点, 隔振器下端位移大幅减小, 表明了设计的隔振器具备一定的隔振能力。
|
| 图 9 激振幅值0.1, 0.25, 0.5 mm时上、下端位移 |
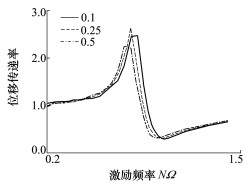
采用位移传递率评估隔振器的隔振能力, 3种位移条件下隔振器在不同频率下的传递率如图 10所示。在3种不同幅值激励位移下, 液弹隔振器位移传递率曲线变化趋势一致; 在液弹隔振器反共振点, 约0.96NΩ处保持了较好的隔振效果, 位移传递率在30%左右。
|
| 图 10 位移传递率随激励幅值变化 |
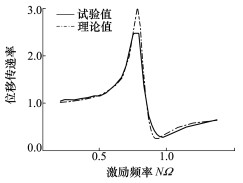
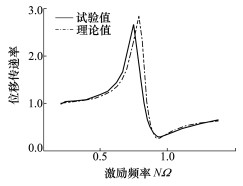
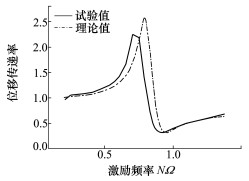
采用公式(9)计算隔振器理论位移传递率, 并与试验结果比较, 验证模型的准确性, 其中橡胶等参数已在文献[18]中测得。图 11~13为3种激振幅值下位移传递率理论值与试验值。由图可知, 3种位移下, 反共振点附近位移传递率理论计算与试验值保持良好的一致性, 且反共振频率点理论值与试验值误差不超过5%, 在工程应用许可的误差范围内。
|
| 图 11 幅值0.1 mm时理论与试验对比 |
|
| 图 12 幅值0.25 mm时理论与试验对比 |
|
| 图 13 幅值0.5 mm时理论与试验对比 |
由前述传递特性的分析可知, 为保证液弹隔振器隔振频率与直升机主振动频率一致, 以求达到更好的隔振效果, 可通过改变K2来精确控制隔振频率。弹簧刚度K2由体积补偿腔内充压气体提供, 如果改变体积补偿腔压强, 则可精确控制K2刚度, 达到调频效果。
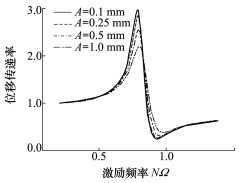
图 14为不同幅值激励位移A下获得的液弹隔振器理论位移传递率, 为充分展示激励位移幅值对传递率的作用, 分别设置幅值为0.1, 0.25, 0.5和1.0 mm。图 14最显著的特点是随着激励位移幅增大, 反共振点位移传递率相应增加(隔振能力降低); 相应地, 共振点最大振幅降低; 整个曲线“坡度”趋于平缓。图 10所示各个激励位移下的试验位移传递率有力地支持这一点: 激励位移幅值从0.1 mm提高到0.5 mm, 位移传递率由28.9%增加到31.9%。这一现象的根源在于相同的激振频率下, 位移幅值越大, 惯性通道内液体流动速度越快, 导致黏性阻尼增加, 从而降低了隔振效果。
|
| 图 14 各激励位移幅值A下位移传递率 |
本文对组合式液弹隔振器进行了理论建模, 采用Lagrange推导液弹隔振系统控制方程并获得隔振器位移传递率及最佳隔振频率。结合某民用直升机旋翼系统振动特性, 分析了设计参数对隔振传递特性的影响, 在此基础上设计并制作液弹隔振器。采用位移传递率作为准则, 以试验的方式评估了液弹隔振器隔振性能, 并探讨激励位移幅值对隔振性能的影响。
计算结果表明, 隔振器设计参数K1, K2, m, R1和R2等参数会影响隔振器最佳隔振频率, 同时包含隔振器阻尼c在内的隔振器参数会影响隔振器在旋翼主振频率NΩ处的传递率大小, 进而影响隔振器的隔振效率。针对某一隔振频率, 需综合各设计参数之间的关系以达到在该频率处的最佳隔振效率。
试验结果表明, 液弹隔振器可隔离约70%的轴向振动(位移传递率约30%), 能大幅降低隔振器上端位移向下端的传递, 可以有效地降低研究对象的振动水平, 是一种有效的振动控制方式。理论建模结果与试验保持一致, 最佳隔振频率和位移传递率与试验数据吻合较好。
| [1] |
张晓谷. 直升机动力学设计[M]. 北京: 航空工业出版社, 1995.
ZHANG Xiaogu. The design of helicopter dynamics[M]. Beijing: Aviation Industry Press, 1995. (in Chinese) |
| [2] |
张呈林, 张晓谷, 郭士龙, 等. 直升机部件设计[M]. 南京: 南京航空航天大学出版社, 2008.
ZHANG Chenglin, HANG Xiaogu, GUO Shilong, et al. The design of helicopter components[M]. Nanjing: Nanjing University of Aeronautics and Astronautics Press, 2008. (in Chinese) |
| [3] | HALWES D R. Live-liquid inertia vibration eliminator[C]//American Helicopter Society 36th Annual Forum, Washington, 1980 |
| [4] | LI Weihua, ZHANG Xianzhou, DU Haiping. Development and simulation evaluation of a magnetorheological elastomer isolator for seat vibration control[J]. Journal of Intelligent Material Systems and Structures, 2012, 23(9): 1041-1048. DOI:10.1177/1045389X11435431 |
| [5] | YANG Jian, DU Haiping, LI Weihua, et al. Experimental study and modeling of a novel magnetorheological elastomer isolator[J]. Smart Material and Structures, 2013, 22: 117001. DOI:10.1088/0964-1726/22/11/117001 |
| [6] | TAMER Aykut, VINCENZO Muscarello, PIERANGELO Masarati, et al. Evaluation of vibration reduction devices for helicopter ride quality improvement[J]. Aerospace Science and Technology, 2019, 95: 105456. DOI:10.1016/j.ast.2019.105456 |
| [7] |
邓旭东. 直升机高性能主减隔振系统分析与仿真研究[D]. 南京: 南京航空航天大学, 2010 DENG Xudong. Research on simulation for the advanced helicopter gearbox isolation system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese) |
| [8] | KYLE R. Vibration analysis and testing of bell 429 helicopter[C]//American Helicopter Society 66th Annual Forum, Phoenix Arizona, 2010 |
| [9] | RODRIGUES Jonathan, CRANGA Paul, CHESNE Simon, et al. Hybrid active suspension system of a helicopter main gearbox[J]. Journal of Vibration and Control, 2016, 24(5): 956-974. |
| [10] | MCGURIE Dennis P. High stiffness ("Rigid") helicopter pylon vibration isolation systems[C]//American Helicopter Society 59th Annual Forum, Phoenix, Arizona, 2003 |
| [11] | HAN Dong, RAHN Christopher D, SMITH Edward C. Higher harmonic pitch link loads reduction using fluidlatic isolators[J]. Journal of Aerospace Engineering, 2014, 228(3): 455-469. |
| [12] | SUN S S, YANG J, LI W H, et al. Development of an isolator working with magnetorheological elastomers and fluids[J]. Mechanical Systems and Signal Processing, 2017, 83: 371-384. DOI:10.1016/j.ymssp.2016.06.020 |
| [13] | LENG Dingxin, SUN Songlei, XU Kai, et al. A physical model of magnetorheological elastomer isolator and its dynamic analysis[J]. Journal of Intelligent Material Systems and Structures, 2020, 31(9): 1141-1156. DOI:10.1177/1045389X20910272 |
| [14] |
龚亮. 液弹隔振器设计分析与试验研究[D]. 南京: 南京航空航天大学, 2010 GONG Liang. Design and testing of the fluid elastomer isolator[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese) |
| [15] |
冯志壮, 钱峰, 程起有, 等. 新型液弹隔振器设计与仿真[J]. 航空学报, 2017, 38(增刊1): 721530.
FENG Zhizhuang, QIAN Feng, CHENG Qiyou, et al. Design and simulation for new fluid elastomer vibration isolator[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(suppl 1): 721530. (in Chinese) |
| [16] | CHENG Qiyou, DENG Jinghui, QIAN Feng, et al. Dynamic performance analysis and design for a fluidlastic isolator[C]// International Conference on Robotics, Control and Automation, Guangzhou, China, 2019: 26-28 |
| [17] | CHENG Qiyou, DENG Jinghui, FENG Zhizhuang, et al. Analysis of material parameter effects on fluidlastic isolators perfor-mance[C]// International Conference on New Material and Chemical Industry, 2018 |
| [18] |
钱峰, 程起有, 代志雄. 液弹隔振器设计与试验分析[J]. 装备环境工程, 2020(9): 52-57.
QIAN Feng, CHENG Qiyou, DAI Zhixiong. Design and test analysis of fluidlastic isolator[J]. Equipment Environmental Engineering, 2020(9): 52-57. (in Chinese) |
| [19] | DENG Jinghui, Cheng Qiyou. Sensitivity analysis of design parameters on fuidlasic isolators pemormce[C]//International Workshop on Materials, Chemistry and Engineering, 2018 |
| [20] | DENG Jinghui, Cheng Qiyou. Analysis of design parameters effects on vibration characteristics of fluidlastic isolators[C]//International Conference on Mechanics and Mechatronics Research, 2017 |



