2. 山东大学 齐鲁交通学院, 山东 济南 250002;
3. 中国矿业大学(北京) 力学与建筑工程学院, 北京 100083
钢筋混凝土结构或构件中裂纹的存在极大影响了结构的正常使用与耐久性,当裂纹宽度达到一定程度时还可能危及结构安全。研究发现钢筋混凝土结构或构件在荷载作用下的宏观断裂失效特征与其在变形时内部微裂纹的萌生、拓展和演化密切相关。在外力作用下由材料内部起始损伤引起的应力集中,将导致裂纹不断拓展以致失稳破坏,因此钢筋混凝土材料的破坏本质上是裂纹的拓展失稳过程[1-2]。一般来讲,混凝土中的裂纹是由内部微观孔洞成核造成的,这些孔洞一般产生于混凝土内部存在初始缺陷的位置处,当钢筋混凝土结构承受温度变化、化学侵蚀等不良环境条件或外界荷载作用时,结构中便可能出现微观缺陷并逐渐演化形成微裂纹,随荷载持续增大,微观裂纹逐渐扩展延伸形成宏观断裂,进而导致结构开裂破坏[3]。目前,常采用弹塑性有限元法计算钢筋混凝土结构或构件在外荷载作用下的塑性区[4],然而对裂纹扩展及断裂失效机理的研究目前仍不成熟。
自20世纪60年代Barenblatt和Dugdale提出内聚力模型理论[5-6]以来,经过近几十年的发展,针对不同的材料性质或结构形式演化出了不同形式的内聚力模型,尤其裂纹尖端塑性区概念的提出很好地解决了线弹性断裂在裂纹尖端引起的应力奇异问题[7]。在这些研究成果当中不乏考虑材料细观结构的数值分析以及实验研究,例如Yu等[8]应用显式算法来模拟钢筋混凝土梁的裂纹扩展,预先设置裂纹位置,并在裂纹位置处嵌入内聚力单元,利用双线性本构模型来描述内聚力单元的演化规律,研究静荷载作用下三点弯曲梁的破坏演化规律;Billy[9]建立二维数值模型并引入断裂能,利用内聚力模型研究预制裂纹条件下三点、四点弯曲梁的断裂破坏形态,结果表明内聚力模型适用于研究混凝土梁裂纹扩展及断裂破坏问题;Carpinteri等[10-11]做了大量的钢筋混凝土梁破坏实验,并将内聚力模型应用到钢筋混凝土梁中,分析钢筋混凝土梁从裂纹萌生到钢筋屈服的断裂失效机制,得出了钢纤维混凝土梁在无筋,少筋,适筋、超筋条件下的应力应变曲线。
本研究基于内聚力模型理论[12-14],采用数值模拟与试验相结合的方法,研究了钢筋混凝土三点、四点弯曲梁在荷载作用下的裂纹扩展规律,验证了内聚力模型在模拟钢筋混凝土结构断裂破坏中的适用性,为分析钢筋混凝土结构破坏机理提供一种新的途径。同时重点分析了钢筋混凝土梁在不同配筋率和螺旋箍筋倾角条件下梁体的裂纹分布、扩展规律及破坏形式,为优化混凝土结构设计提供参考依据。
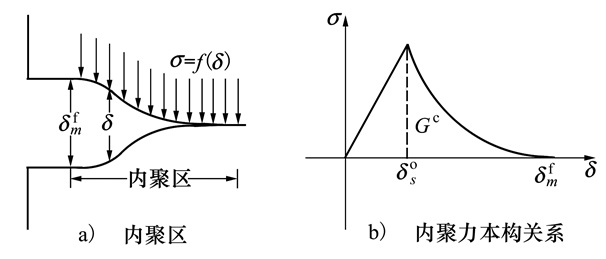
1 内聚力模型内聚力模型将裂纹视为两部分, 一部分为彻底分离的2个自由面, 在裂纹尖端作用着内聚力σ, 致使材料开裂后并不立即完全断开, 这一部分即为内聚区, 如图 1所示。在内聚区存在小于某一临界值δmf的裂纹张开位移δ, 内聚力σ被定义成裂纹张开位移δ的函数, 称σ-δ之间的关系为牵引分离法则。当内聚区开始承载时, 内聚力σ随着裂纹张开位移δ的增大逐渐增大, 当裂纹张开位移达到δmo, 意味着材料开始出现损伤, 随后随着裂纹张开位移增大内聚力开始减小至零, 此时断裂能达到材料破坏所需的临界断裂能GC(断裂能为σ-δ曲线所包含的面积, 即GC=∫σdδ=∫f(δ)dδ), 此时内聚力单元完全断开, 结构萌生裂纹。
|
| 图 1 内聚力模型示意图 |
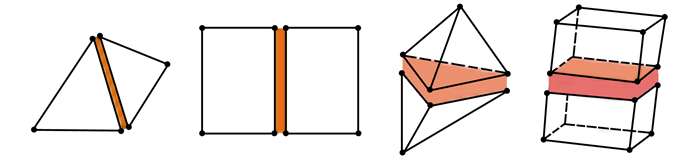
内聚力单元是在相邻有限元之间嵌入的一种无厚度单元, 如图 2所示。内聚力单元与有限元之间存在网格拓扑上的联系, 但二者的本构关系相互独立, 结合内聚力模型理论, 其天然地适用于描述外荷载作用下材料内部由于裂纹萌生拓展导致的失效破坏问题。
|
| 图 2 内聚力单元与常见有限元兼容 |
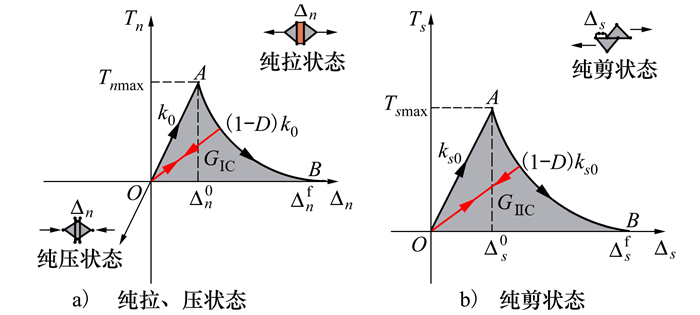
内聚力单元的本构关系通过牵引-分离、损伤起始和损伤演化3个阶段来定义。当内聚力单元的应力状态满足损伤起始准则后就进入损伤演化阶段, 直至内聚力单元达到破坏标准并被移除, 从而在此位置处形成裂纹。内聚力单元在纯拉、压应力以及纯剪应力作用下的本构响应如图 3所示。
|
| 图 3 内聚力单元的本构响应 |
内聚力单元的牵引-分离阶段对应图 3中的OA段, 该阶段内聚力单元表现出线弹性的本构关系, 可用(1)式表示
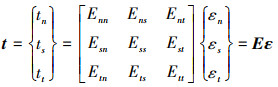
|
(1) |
式中: t为内聚力单元牵引应力矢量, 由法向应力tn和2个切向应力ts, tt组成; ε为内聚力单元应变矢量, 由法向应变εn和切向应变εs, εt构成; E为内聚力单元弹性矩阵。
1.2.2 损伤起始准则内聚力单元由损伤起始阶段进入损伤演化阶段的判断标准称之为最大名义应力准则, 可表示为

|
(2) |
式中: tn, ts, tt分别表示内聚力单元法向应力和2个切向应力; tnmax, tsmax, ttmax分别表示内聚力单元法向和切向所能承受的最大应力; Macaulay括号〈·〉表示括号内变量取值始终不小于0,从而实现内聚力单元在纯压状态下不会出现损伤破坏。
1.2.3 损伤演化阶段损伤演化阶段对应图 3中的AB段, 当内聚力单元的应力状态满足最大名义应力准则后即进入损伤演化阶段, 该阶段引入损伤变量D来描述内聚力单元刚度的折减, 在材料损伤演化过程中, D从0单调增加至1。内聚力单元各应力分量与损伤变量的关系可表示为
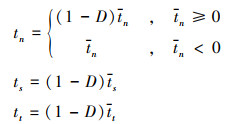
|
(3) |
式中: tn, ts, tt分别为不考虑损伤情况下, 根据牵引-分离阶段的线性本构关系计算所得的法向和切向应力分量。
为了描述内聚力单元在法向和切向变形的共同作用下发生的损伤演化, 引入有效位移δm, 其表达式为
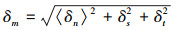
|
(4) |
通过指定材料断裂失效时的断裂能G来定义损伤演化, 损伤演化形式由损伤变量D的表达式确定。
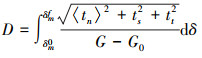
|

|
(5) |
式中: δm0为损伤起始时对应的裂纹张开位移; δmf为内聚力单元移除时对应的裂纹张开位移; Teff0为损伤初始时的有效牵引应力; G0为损伤起始时的弹性能。
2 钢筋混凝土梁三维数值分析 2.1 模型验证根据Vecchio和Bresler等的试验[15-16], 建立钢筋混凝土三点弯曲梁模型, 梁的纵筋配筋率ρs为1.7%, 混凝土单元采用实体单元(C3D4), 钢筋采用桁架单元(T3D2), 钢筋本构为累积损伤演化模型。利用开发的内聚力单元嵌入程序将内聚力单元批量嵌入到有限元模型中, 为避免单元断裂失效后发生穿透现象, 在所有实体单元间均设置通用接触, 数值计算时以1 mm/s的速率匀速加载直至破坏。计算所采用单元材料属性见表 1~2。
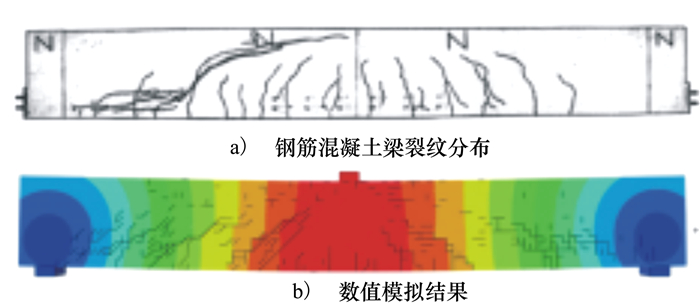
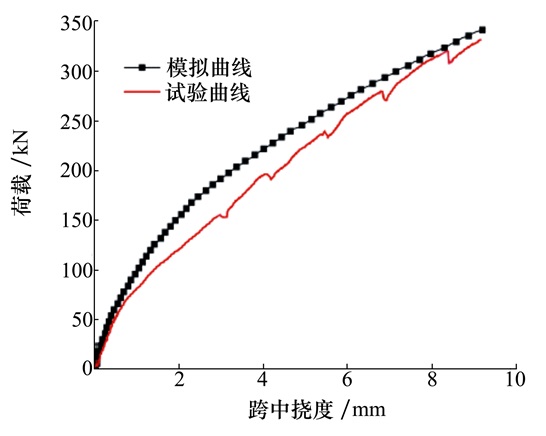
数值模拟与试验所得钢筋混凝土梁的裂纹分布基本吻合, 如图 4所示。梁跨中实测荷载挠度曲线与模拟曲线的对比如图 5所示, 二者整体趋势相同, 但模拟曲线略高于实测结果, 原因在于实际梁体中可能存在各种孔洞及微裂纹等缺陷, 而数值模拟假定混凝土为均质材料, 且未考虑钢筋与混凝土之间的相对滑移。但无论是从物理形态上还是力学性态上来看, 模拟结果均能较好地描述梁体的破坏, 可见内聚力模型适用于模拟钢筋混凝土结构断裂破坏等问题, 其优势在于能够再现梁体裂纹萌生、扩展直至破坏的全过程。
|
| 图 4 数值模拟与原型试验钢筋混凝土梁裂纹分布对比图 |
|
| 图 5 钢筋混凝土梁荷载位移关系曲线 |
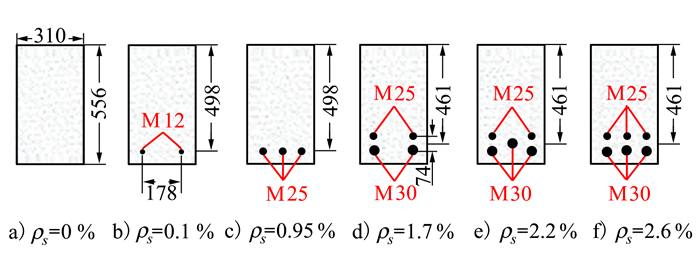
为研究纵筋配筋率对混凝土受力性能的影响, 分别建立配筋率ρs等于0%, 0.1%, 0.95%, 1.7%, 2.2%, 2.6%的模型。图 6为不同配筋率梁的横截面示意图, M12表示纵筋直径为12 mm, 以此类推。数值计算选用的模型、参数以及加载条件等与前节相同。
|
| 图 6 钢筋混凝土梁横截面钢筋布局 |
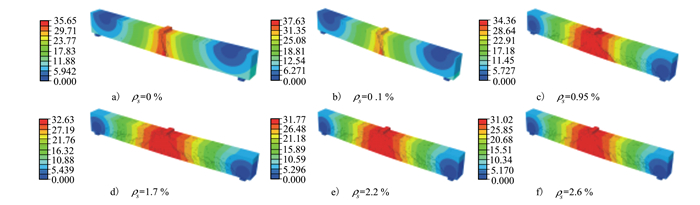
不同配筋率梁体破坏时的裂纹大致对称分布, 如图 7所示。从细节上对比分析可以发现: ①无筋梁(ρs=0)及低配筋梁(ρs=0.1%)均在跨中形成了一条明显的张拉主裂纹, 此裂纹大致沿加载中心线由梁底部扩展到加载板中心点, 受网格尺寸大小的影响, 裂纹略有倾斜, 裂纹拓展迅速, 表现出脆性断裂的破坏特征; ②当配筋率为0.95%, 1.7%和2.2%时, 在梁右侧约1/4跨处形成一条延伸到加载中心点处的主斜裂纹, 倾斜角度约为45°, 扩展深度接近3/4梁高, 继续加载会使梁截面沿主斜裂纹破坏, 表现出适筋梁的延性破坏特征; ③当配筋率为2.6%时, 随荷载的增大, 受拉纵筋还未屈服, 加载板附近的混凝土已经压坏, 表现出超筋梁脆性断裂的破坏特性。上述现象说明当配筋率相对较低时, 受拉区钢筋首先达到屈服状态, 梁体的承载能力降低, 进而引起受拉区混凝土开裂。配筋率高时, 随荷载的施加, 在受拉区钢筋还未达到屈服状态的情况下, 支座附近的剪应力便已经引起斜裂纹的发育。
|
| 图 7 不同配筋率下钢筋混凝土梁位移云图 |
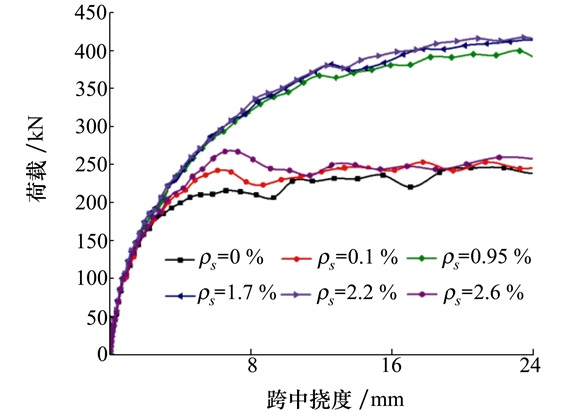
从图 8荷载-挠度关系曲线上来看, 加载初期, 内聚力单元还未达到损伤起始准则的标准, 模型整体处于弹性变形阶段, 不同配筋率条件下梁体的荷载位移曲线基本一致, 呈现出线性增长的趋势。持续加载, 内聚力单元出现损伤, 继而进入损伤演化并最终破坏移除, 此时荷载位移曲线因配筋率的不同出现2种不同的趋势: ①当配筋率小于0.95%或大于2.2%时, 梁体的承载能力无法持续增长, 有着较长的平台期, 结合破坏形式来看, 符合脆性断裂特征; ②当配筋率在0.95%~2.2%时, 荷载位移曲线之间区别较小, 承载能力持续增长, 但增长速率变缓; 上述现象说明少量和超量配筋均会使钢筋混凝土梁表现出脆性破坏的特征, 而配筋率适中则能充分发挥钢筋混凝土梁的延性特征, 更有利于梁体承载。
|
| 图 8 不同配筋率钢筋混凝土梁的荷载-挠度关系曲线 |
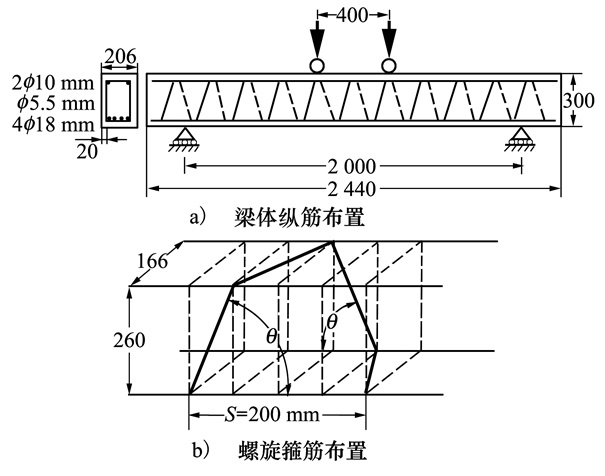
为提高钢筋混凝土梁斜截面的抗剪性能, 针对新的箍筋形式进行研究, 此箍筋形式通过改变箍筋的倾斜角度而定义, 因而命名为螺旋箍筋。基于Shatarat所做的四点弯曲梁的原型试验[19]进行模拟分析, 探讨相同箍筋间距、倾角θ分别为70°, 75°, 80°, 85°, 90°的螺旋箍筋对钢筋混凝土梁斜截面抗剪性能的影响。原型试验梁体尺寸为2 440 mm×206 mm×300 mm, 梁体上部布设2根直径10 mm的纵向钢筋, 下部布设4根直径18 mm的纵向钢筋, 箍筋直径5.5 mm, 钢筋保护层厚度20 mm。梁体支撑在间隔2 000 mm的支座上, 上部两加载端间距400 mm, 如图 9a)所示。螺旋箍筋间距S为200 mm, 其具体构造如图 9b)所示。数值计算以1 mm/s的速率匀速加载直至模型破坏, 钢筋参数见表 3。
|
| 图 9 梁体及螺旋箍筋细部构造 |
| 钢筋 | 密度/(kg·m-3) | 弹性模量E/GPa | 屈服强度fy/MPa | 极限强度fu/MPa |
| 纵筋 | 7 800 | 200 | 455 | 615 |
| 箍筋 | 7 800 | 200 | 290 | 400 |
篇幅所限, 仅给出螺旋箍筋倾角为70°时的计算结果, 如图 10所示。宏观上看, 裂纹扩展模式大致都是从支座附近向加载板处延伸形成2条明显的斜裂纹, 发生剪切破坏。数值模拟结果能够很好地再现试验结果中2条主斜裂纹扩展情况。

|
| 图 10 螺旋箍筋倾角70°的梁体破坏形态 |
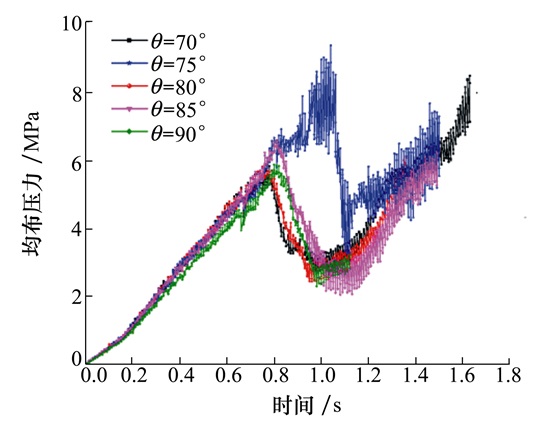
加载初期, 由于梁体内钢筋与混凝土协同作用, 各工况荷载基本都保持线性增长的态势, 箍筋角度的改变在这一阶段对梁体力学性态的影响并不明显, 如图 11所示。继续加载, 混凝土发生剪切破坏, 各曲线出现骤降段, 但由于底部钢筋的作用荷载又逐渐增长。从曲线中可以明显观察到, 箍筋倾角为80°时梁体所能承受的荷载最大而且达到峰值荷载所需的时间更长, 表明梁体的延性得到了较好改善, 所以最优的螺旋箍筋倾角为80°, 这与原型试验结果是一致的。
|
| 图 11 不同螺旋箍筋倾角下压力-时间关系曲线 |
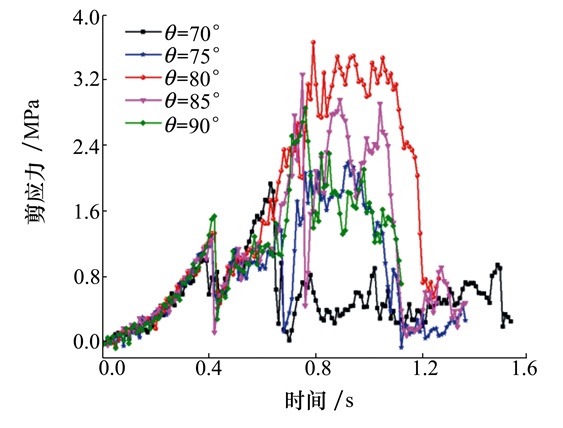
从图 12剪应力-时间关系曲线来看, 加载前期(0.6 s前), 不同工况下梁体剪应力随时间变化的曲线基本吻合; 0.6 s后, 各条曲线出现较大波动, 但剪应力波动的水平并不在同一层次, 可以发现剪应力大小随螺旋箍筋倾角的不同呈现出如下规律: τ80° > τ85° > τ90°≈τ75° > τ70°。说明相对于传统的平行箍筋(90°)形式而言, 螺旋箍筋倾角在75°~90°之间时, 有助于提高梁体抗剪能力, 螺旋箍筋倾角小于75°, 反而不利于梁体抗剪能力的提高。最优的螺旋箍筋倾角为80°, 这与图 12中得出的结论一致。
|
| 图 12 梁体斜截面剪应力-时间关系曲线 |
本文基于内聚力模型理论研究了钢筋混凝土三点弯曲梁在不同配筋率条件下以及四点弯曲梁在不同螺旋箍筋倾角条件下, 梁体裂纹分布、扩展规律和破坏形式, 得出以下结论:
1) 内聚力模型适用于钢筋混凝土结构破坏模拟, 其优势在于能够全过程描述结构裂纹萌生直至演化破坏, 并且可以有效预测梁体在荷载作用下的变形趋势。
2) 无筋梁(ρs=0)和低配筋梁(ρs=0.1%)承载时具有明显的张拉主裂纹, 脆性断裂特征显著; 适筋梁(ρs=0.95%, 1.7%, 2.2%)承载时呈现出较长的屈服阶段, 延性断裂力学性态显著; 配筋率(ρs=2.6%)较高时, 荷载挠度曲线相对适筋梁并未有明显提升, 随外荷载增大钢筋尚未达到屈服强度, 加载板处的混凝土已被压碎, 表现出脆性断裂的破坏特征。
3) 最优螺旋箍筋倾角为80°, 此时钢筋混凝土梁正截面和斜截面承载能力最大; 倾角在80°~90°之间, 梁体抗剪承载力随螺旋箍筋倾角增大而逐渐减小; 倾角在70°~80°之间, 梁体抗剪承载能力随螺旋箍筋倾角增大而逐渐增大。
| [1] | KUMAR S, BARAI S V. Concrete fracture models and applications[M]. Berlin: Springer Berlin Heidelberg, 2011. |
| [2] | LI Min. Effects of rate-dependent properties of material on dynamic properties of reinforced concrete structural[J]. Dalian: Dalian University of Technology, 2012. |
| [3] | SWARTZ S E, TAHA N M. Mixed mode crack propagation and fracture in concrete[J]. Engineering Fracture Mechanics, 1990, 35. |
| [4] | CHO C G, HOTTA H. A study on compressive strength of concrete in flexural regions of reinforced concrete beams using finite element analysis[J]. Structural Engineering & Mechanics, 2002, 13(3): 313-328. |
| [5] | BARENBLATT G I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks[J]. Journal of Applied Mathematics and Mechanics, 1959, 23(3): 434-444. |
| [6] | DUGDALE D S. Yielding of steel sheets containing slits[J]. Journal of Mechanics Physics of Solids, 1960, 8(2): 100-104. DOI:10.1016/0022-5096(60)90013-2 |
| [7] | HILLERBORG A, MODEER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement & Concrete Research, 1976, 6(6): 773-781. |
| [8] | YU R C, RUIZ G. Explicit finite element modeling of static crack propagation in reinforced concrete[J]. International Journal of Fracture, 2006, 141(3/4): 357-372. |
| [9] | BILLY C. Simulation of crack growth using cohesive crack method[J]. Applied Mathematical Modelling, 2010, 34(9): 2508-2519. DOI:10.1016/j.apm.2009.11.015 |
| [10] | CARPINTERI A, El-KHATIEB M, CADAMURO E. Failure mode transitions in RC beams: a cohesive/overlapping crack model application[J]. Meccanica, 2013, 48(10): 2349-2366. DOI:10.1007/s11012-013-9753-4 |
| [11] | CARPINTERI A, CADAMURO E, VENTURA G. Fiber-reinforced concrete in flexure: a cohesive/overlapping crack model application[J]. Materials & Structures, 2015, 48(1/2): 235-247. |
| [12] | CHANG Xin, REN Mingfu, GUO Xu. A cohesive zone model for self-similar fractal crack propagation[J]. Journal of Mechanical Science & Technology, 2017, 31: 4763-4769. |
| [13] | WU J, RU C Q. A modified cohesive zone model for a high-speed expanding crack[J]. Fatigue & Fracture of Engineering Materials & Structures, 2014, 37(9): 1013-1024. |
| [14] | ANDREAS B, STEPHAN R, MEINHARD K. Cohesive zone modeling of stable crack propagation in highly ductile steel[J]. Key Engineering Materials, 2018, 774: 167-172. DOI:10.4028/www.scientific.net/KEM.774.167 |
| [15] | VECCHIO F J, SHIM W. Experimental and analytical reexamination of classic concrete beam tests[J]. Journal of Structural Engineering, 2004, 130(3): 460-469. DOI:10.1061/(ASCE)0733-9445(2004)130:3(460) |
| [16] | BRESLER B, SCORDELIS A C. Shear strength of reinforced concrete beams[J]. ACI Structural Journal, 1963, 111(4): 809-818. |
| [17] | GUO L, XIANG J, LATHAM J P, et al. A numerical investigation of mesh sensitivity for a new three-dimensional fracture model within the combined finite-discrete element method[J]. Engineering Fracture Mechanics, 2016, 151: 70-91. DOI:10.1016/j.engfracmech.2015.11.006 |
| [18] |
张娟霞, 唐春安, 梁正召, 等. 受拉钢筋混凝土构件破坏过程的数值模拟[J]. 计算力学学报, 2007(4): 453-458.
ZHANG Juanxia, TANG Chun'an, LIANG Zhengzhao, et al. Numerical simulation of failure process of reinforced concrete specimen under uniaxial tension[J]. Chinese Journal of Computational Mechanics, 2007(4): 453-458. (in Chinese) DOI:10.3969/j.issn.1007-4708.2007.04.013 |
| [19] | SHATARAT N, KATKHUDA H, ABDEL-JABER M, et al. Experimental investigation of reinforced concrete beams with spiral reinforcement in shear[J]. Construction & Building Materials, 2016, 125: 585-594. |
2. School of Qilu Transportation, Shandong University, Jinan 250002, China;
3. School of Mechanics and Civil Engineering, China University of Mining and Technology, Beijing 100083, China




