2. 中国航天科技集团有限公司 航天进入、减速与着陆技术实验室, 北京 100094
充气式返回舱是一种新型的气动减速装置, 再入大气时利用充气形成气动外形, 并由表面耐高温柔性材料提供热防护, 最后由自身的充气结构实现着陆缓冲。充气式返回舱集合了传统飞行器的热防护系统、降落伞减速系统以及着陆/着水缓冲系统, 简化了航天器回收系统的设计[1]。充气式返回舱拓展了传统航天器回收着陆技术, 具有广泛的应用前景, 各航天大国均开展了广泛的研究[2-8], 我国也在2020年5月用长征五号B运载火箭进行了首次柔性充气式货物返回舱搭载试验。
不同于传统的刚性结构返回舱, 充气式返回舱是由柔性材料制成, 在高速气流的冲击下, 柔性结构会发生变形甚至破坏。因此, 充气式返回舱的结构和防热的设计十分重要, 而获得准确的流场特性参数是进行充气式返回舱结构和防热设计的重要前提。相比于实验研究, 数值模拟能够快速获得充气式返回舱的流场特性参数, 缩短研制周期, 降低研制成本。为获得准确可靠的充气式返回舱流场特性参数, 建立合理的数值仿真模型, 选择合理的物性参数十分重要。目前充气式返回舱大气再入气动特性仿真大多基于理想气体假设, 黏性系数和热导率等物性参数采用Sutherland公式[9-13]。通常情况, 常温下空气的黏性和热导率可采用Sutherland公式计算, 但当温度进一步升高时, 空气中的氧气和氮气将发生解离反应, 更高温度时将发生电离反应, 这一系列的化学反应使空气物性发生复杂变化, Sutherland公式将不再适用[14]。充气式返回舱高速再入时流场温度非常高[15], 若采用Sutherland公式计算空气物性参数会带来巨大误差。因此, 为了获得准确的气动特性参数, 首先需要获得高温下空气的物性参数。
为解决高温条件下空气物性参数的计算问题, 学者们已经进行了深入研究[16-19], 目前应用较为广泛的是Gupta的高温空气拟合关系式[17], 该拟合关系式已经被广泛应用于超声速等离子体风洞、电弧加热器、圆柱绕流以及平板边界层流动等领域的研究[14, 20-22]。
本文分别采用Gupta的高温空气拟合关系式和Sutherland公式计算空气的物性参数, 对充气式返回舱高速再入流场进行数值模拟研究, 比较采用这两种空气物性参数计算方法获得的流场特性参数差异, 进而为充气式返回舱的工程设计提供一定的理论参考。
1 计算模型本文采用二维数值模拟对充气式返回舱气动特性进行研究, 求解可压缩N-S方程, 在笛卡尔坐标系下控制方程可以写成如下形式
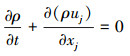
|
(1) |
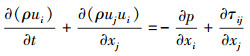
|
(2) |
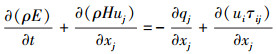
|
(3) |
式中: ρ为流体密度;xi为笛卡尔坐标; ui为速度分量; p为压强; E为内能; H为焓值; τij和qi分别为黏性应力项和热通量项。
湍流模型采用k-ω模型, 模型输运方程如(4)~(5)式所示
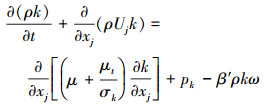
|
(4) |
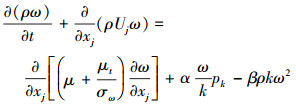
|
(5) |
式中, β′=0.09, α=1.4, β=0.075, σk=2, σω=2。
本文研究的流体介质为空气, 分别采用Sutherland公式和Gupta的拟合公式对方程中涉及到的物性参数进行计算。公式(6)和(7)为Sutherland公式表示的黏性系数和热导率。Gupta拟合公式基于空气11组分模型(O2, N2, O, N, NO, O+, N+, NO+, O2+, N2+, e)计算高温空气物性, 考虑了空气因高温导致的空气化学反应, 温度范围最高达30 000 K[19]。公式(8)和(9)为Gupta拟合公式的黏性系数和热导率。
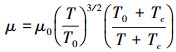
|
(6) |
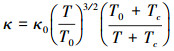
|
(7) |
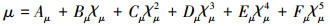
|
(8) |
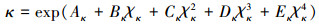
|
(9) |
式中: T, μ, κ分别为温度、黏性系数和热导率; μ0=1.716 1×10-5 Pa·s, κ0=2.415×10-2 W/(m·K); To=273.16 K, Tc=110.4 K, T0为摄氏零度, Tc为参考温度, χμ, χκ, Aμ, Aκ等参数可参考文献[19]。
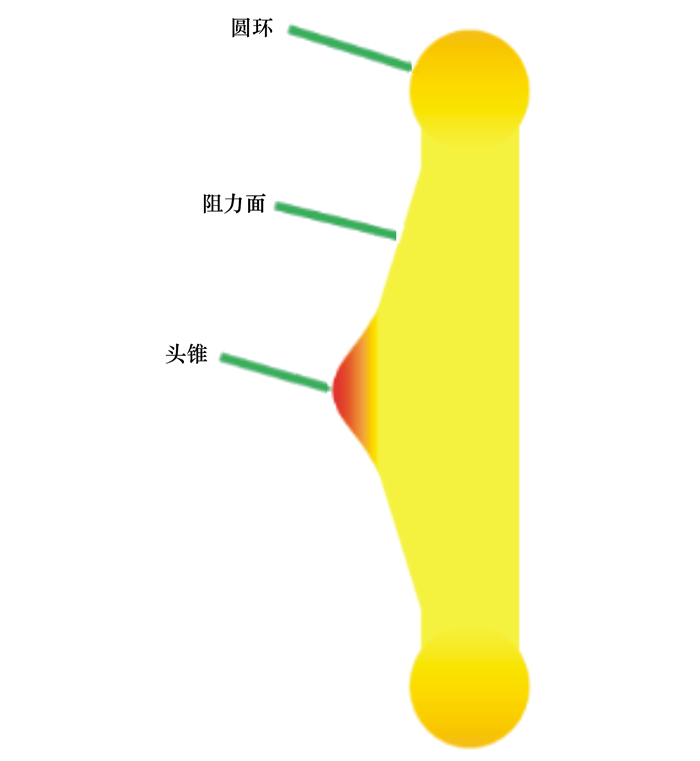
本文以日本研制的充气式返回舱实验模型HWT-MAAC为研究对象, 该模型为飞行演示验证试验中采用的充气式返回舱SMAAC的缩比模型, 其结构示意如图 1所示, 尺寸参数可参见文献[23]。
|
| 图 1 HWT-MAAC模型结构示意图 |
为考察不同温度范围2种物性参数计算方法带来的结果差异, 本文在文献[23]实验工况的基础上, 通过改变来流温度和马赫数来进行计算研究。实验工况为来流温度45 K, 来流马赫数10, 来流压强均为60 Pa, 表 1列出了本文的5个计算工况, 所有计算工况的来流攻角均为0°。
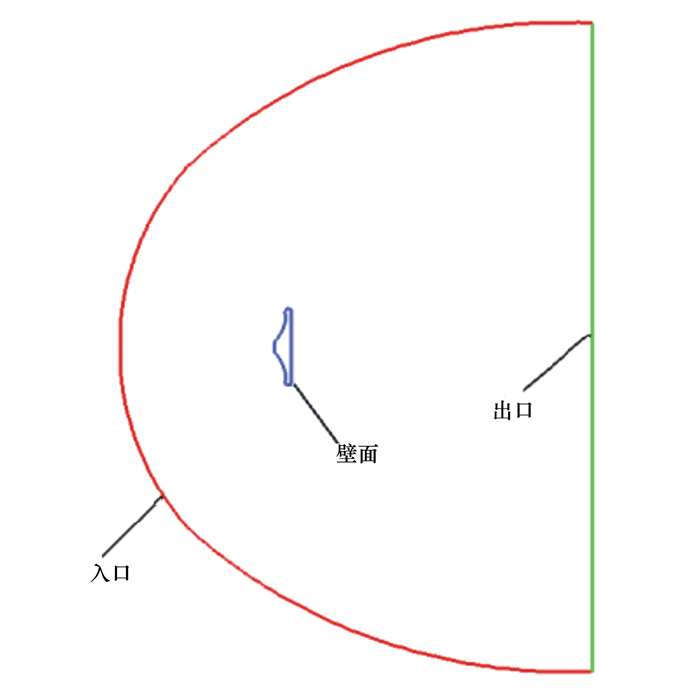
图 2给出了本文的计算域, 计算域为半圆形, 直径约为返回舱直径的10倍, 返回舱前端距计算域前端约为2倍返回舱的直径。本文的计算工况为超声速流动, 流场的扰动不会向上游传播, 计算域能够捕捉完整的激波结构, 则计算域的选取对计算结果的影响较小。计算域入口给定来流马赫数、来流压强以及来流温度, 出口参数外推, 壁面采用无滑移边界条件, 壁面温度为300 K。
|
| 图 2 计算域以及网格划分情况 |
首先本文进行了网格无关性验证, 分别采用网格数为30 000, 60 000以及120 000的网格数量对工况3进行了计算, 同时对近壁网格进行加密保证y+小于1, 比较了沿壁面的热流密度, 比较结果如图 3所示。从图中可以看出网格数量为60 000和120 000的计算结果十分接近, 而网格数量为30 000的计算结果与另外2个相差较远。因此, 为了能够保证计算的准确性, 同时也能节省计算资源, 本文采用网格数量为60 000, 图 4给出了网格划分情况。

|
| 图 3 网格无关性验证 |

|
| 图 4 网格划分(网格量60 000) |
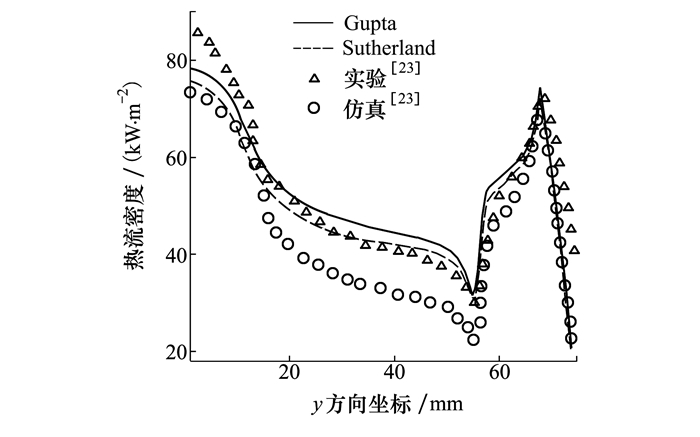
为了验证模型的可靠性, 本文将工况3计算得到的充气式返回舱迎风面的热流密度与文献[23]的实验结果和三维仿真结果进行了比较, 如图 5所示。实验中采用高超声速风洞对充气式返回舱实验模型HWT-MAAC进行了研究, 采用辐射平衡假设对表面热流密度进行测量。从图中看出本文采用Gupta拟合公式和Sutherland公式的计算结果与实验值均符合较好, 在阻力面处, 本文的计算结果比文献[23]的仿真结果略高。
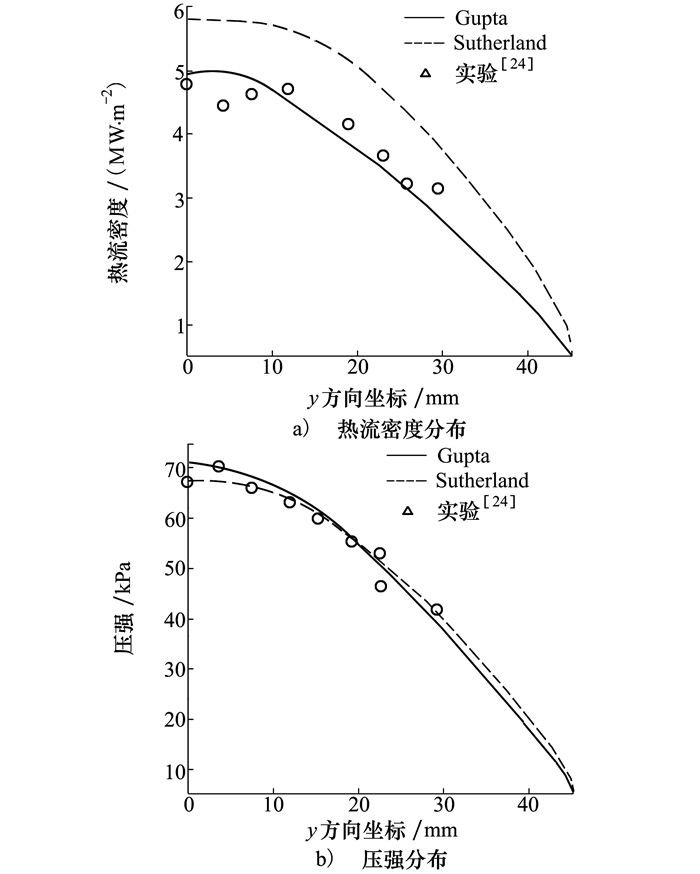
为进一步验证本文模型的可靠性, 本文选择文献[24]的实验结果进行验证, 实验模型为90 mm圆柱体, 采用高焓激波风洞对圆柱体迎风面的热流密度和压强进行了测量, 来流马赫数为8.78, 来流温度694 K, 来流压强为687 Pa, 比较结果如图 6所示。从图中看出采用Gupta拟合公式获得的表面热流密度与实验结果符合得更好, 采用这两种物性计算方法得到的表面压强与实验结果符合均较好。
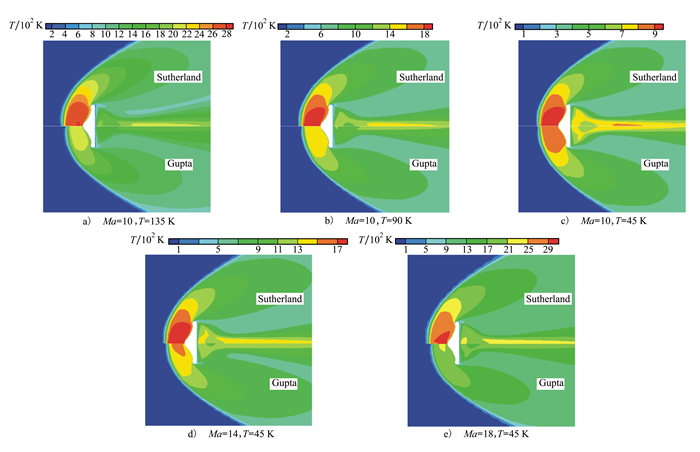
温度对空气物性参数有十分重要的影响, 图 7给出了本文计算工况的温度分布情况, 从图中看出采用Gupta拟合公式计算得到的激波位置更靠近返回舱表面, 流场的温度也显著比Sutherland的计算结果低。另外, 从图中还看出这种差异随着来流马赫数和温度的增加更加明显, 比如工况3的来流马赫数和温度相对来说较低, Gupta拟合公式和Sutherland公式计算结果相对来说也较为接近。工况3中流场最高温度不超过1 000 K, Sutherland公式还能较好地描述空气的物性, Sutherland公式和Gupta拟合公式计算得到的空气物性差别不大。而随着来流马赫数和温度的增加, 流场中的温度逐渐上升, Gupta拟合公式和Sutherland公式计算得到的空气物性参数差别较为明显, 两者计算得到的流场特性差别逐渐显现。
|
| 图 7 流场中温度分布情况 |
对于高超声速激波形状和距离的研究始于20世纪50年代, 涉及理论和实验研究[25]。以大量实验数据为基础得出的激波脱体距离工程算法计算量小, 计算速度快, Inouye[26]建立了多种气体环境下的绕半球体脱体激波距离关系式如(10)式所示
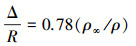
|
(10) |
式中:Δ为激波脱体距离;R为半球半径;ρ∞和ρ分别为波前和波后气体的密度。从这个关系式中可以发现, 脱体激波的距离跟波前和波后气体密度的比值成正比。为探究采用2种物性参数方法计算的激波位置产生差异的原因, 图 8给出了沿流场中心线气体的密度。从图 8中看出在波前采用2种物性参数计算方法得到的密度相差不大, 而在波后Gupta拟合公式计算得到的气体密度大于Sutherland公式计算得到的气体密度, 即Gupta拟合公式获得的波前和波后的气体密度的比值小于Sutherland公式, 因此脱体激波的距离更接近物面。

|
| 图 8 沿中心线气体的密度 |
不管是来流马赫数增加还是来流温度的增加, 流场温度的上升是导致两者计算结果差异的重要因素, 表 2列出了5个工况流场中的最高温度, TG和TS分别表示采用Gupta拟合公式和Sutherland公式计算得到的最高温度, 比较发现随着来流马赫数和温度的增加, 流场中最高温度的差距增加十分明显。产生流场温度差异的主要原因是Gupta拟合公式考虑了空气高温下因振动、解离以及电离等化学反应对物性参数的影响, 空气的这些化学反应能够吸收返回舱外部的部分能量, 导致返回舱外部温度降低。
| 工况 | TG/K | TS/K | (TS-TG)/TG |
| 1 | 2 064 | 2 811 | 36.19% |
| 2 | 1 575 | 1 878 | 19.24% |
| 3 | 875 | 941 | 7.54% |
| 4 | 1 522 | 1 800 | 18.27% |
| 5 | 2 106 | 2 945 | 39.84% |
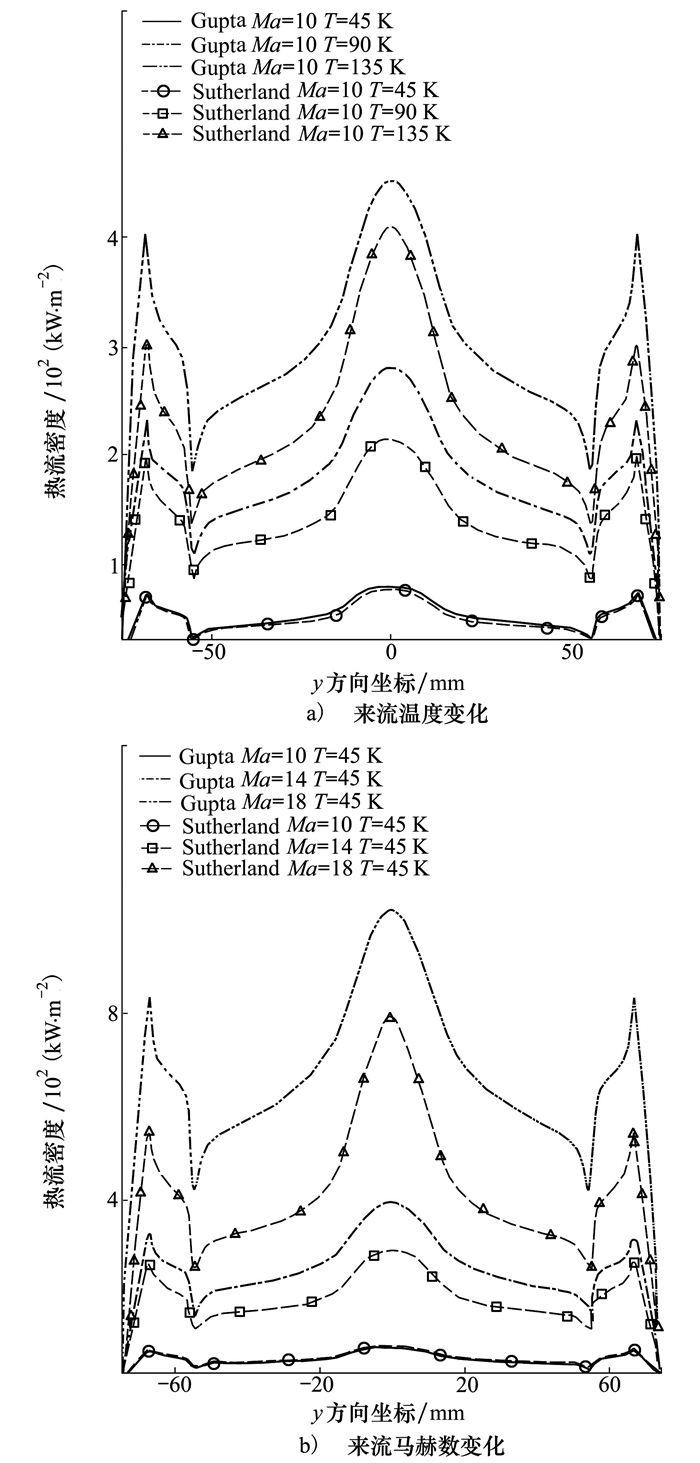
在高速气流冲击下, 充气式返回舱迎风面将承受剧烈的气动力和气动热, 准确的气动热和气动力特性对充气式返回舱的结构和防热设计十分重要。图 9给出了返回舱迎风面的热流密度分布, 从图中看出热流密度在头锥和两侧圆环处均存在峰值, 最大峰值在头锥处。从图中还可以看出返回舱表面的热流密度随着来流马赫数和温度增加上升十分显著, 以Gupta拟合公式计算结果为例, 来流Ma=10, T=45 K, 头锥处峰值的热流密度为79 kW/m2, 来流Ma=10, T=135 K, 头锥处峰值的热流密度为451 kW/m2, 来流Ma=18, T=45 K, 头锥处峰值的热流密度为1 022 kW/m2。比较发现, Sutherland公式计算的热流密度总体上低于Gupta拟合公式的结果, Sutherland公式低估了返回舱表面的热流密度, 如工况5所示, 来流Ma=18, T=45 K, Gupta拟合公式获得的热流密度峰值高出Sutherland公式获得的热流密度峰值29%。其中工况3由于两者计算得到的流场温度相差不大, 两者物性参数差别不大, Gupta公式的计算结果仅略微高于Sutherland公式的结果。
|
| 图 9 返回舱迎风面的热流密度分布 |
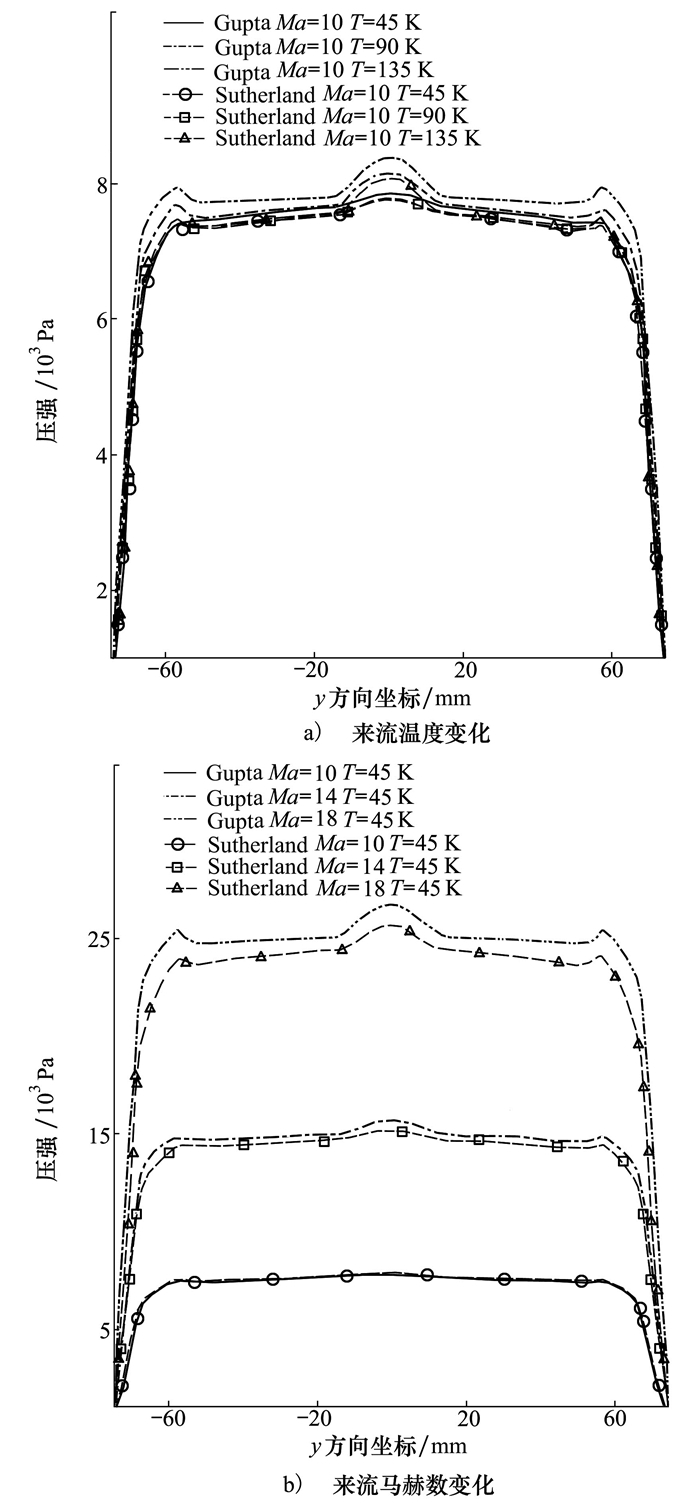
由于返回舱表面的气动力主要来源于表面压强的作用, 图 10给出了返回舱迎风面处的压强分布情况, 从图中看出压强的分布规律与热流密度的分布规律类似, 在头锥和两侧圆环处均存在峰值, 最大峰值在头锥处。从图 10a)中看出, 来流温度对迎风面的压强影响并不大, 迎风面压强随来流温度增加仅略微增加。从图 10b)中看出, 来流马赫数对迎风面压强影响较大, 迎风面的压强随来流马赫数的增加显著上升。比较发现, Gupta拟合公式计算得到的迎风面压强大于Sutherland公式的计算结果, 但相对于表面热流密度的差异, 表面压强的差距并不是很大。
|
| 图 10 返回舱迎风面的压强分布 |
充气式返回舱的柔性热防护系统通常由防热层、隔热层和阻力承力层构成, 最外层的防热层主要用来阻挡热流密内部气囊渗漏, 保持充气结构的形状[27]。准确的气动力和气动热特性是各层材料选择以及材料铺层数量选取的重要参考, Sutherland公式在高温下不再适用, 低估了充气式返回舱表面的热流密度和压力, 则有可能造成设计的充气结构防热性能和强度不足, 因此在高温环境下采用Gupta拟合公式进行研究更为合理。
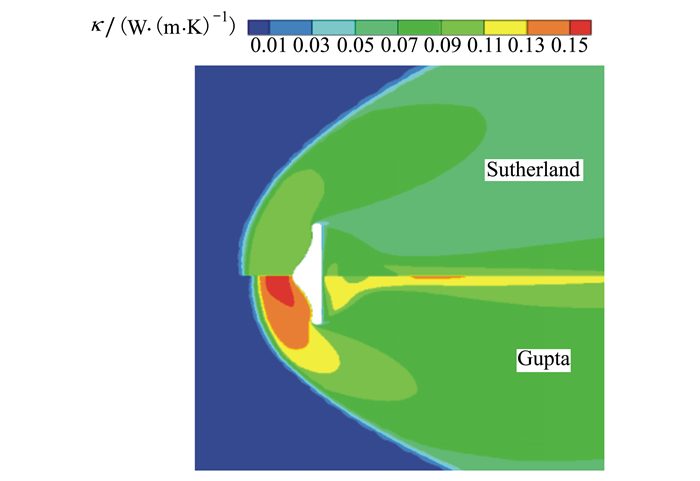
热导率是引起热流密度差异的重要原因, 以工况5为例, 图 11给出了流场中的热导率分布, 从图中看出Gupta拟合公式获得的热导率显著高于Sutherland公式获得热导率, 流场中最大热导率分别为0.152和0.107 W/(m·K)。高温下, 空气的热导率由平动热导率和反应热导率组成, Gupta拟合公式考虑了空气的反应热导[19], 因此采用Gupta拟合公式获得的热导率更大。由图 7可知, Sutherland公式计算得到的流场温度更高, 在近壁区域的温度梯度也更高, 但Sutherland获得的近壁区域热导率比Gupta拟合公式低, 因此导致壁面的热流密度更低。
|
| 图 11 流场中热导率分布情况 |
本文分别采用Gupta拟合公式和Sutherland公式计算空气物性参数, 比较了采用这两种计算公式获得的充气式返回舱流场特性的差异, 研究表明: ①采用Gupta拟合公式获得的激波位置比Sutherland公式的结果更靠近返回舱, 这种差异在高来流马赫数和温度时更加明显; ②采用Gupta拟合公式获得的流场温度更低, 且随着来流马赫数和温度的增加, 流场最高温度的差异更加明显; ③Sutherland公式低估了返回舱迎风面的热流密度, 尤其在来流温度和马赫数较高的工况, Gupta拟合公式获得的热流密度显著高于Sutherland公式的结果, 工况5中Gupta拟合公式获得的热流密度峰值高出Sutherland公式获得的热流密度峰值29%;④Sutherland公式获得的迎风面压强低于Gupta拟合公式的结果, 但是压强的差异相对于热流密度的差异小很多。
| [1] |
卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J]. 宇航学报, 2013, 34(7): 881-890.
WEI Jianzheng, TAN Huifeng, WANG Weizhi, et al. New trends in inflatable reentry aeroshell[J]. Journal of Astronautics, 2013, 34(7): 881-890. (in Chinese) DOI:10.3873/j.issn.1000-1328.2013.07.001 |
| [2] | CLARK I G, HUTCHINGS A L, TANNER C L, et al. Supersonic inflatable aerodynamic decelerators for use on future robotic missions to mars[J]. Journal of Spacecraft and Rockets, 2009, 46(2): 340-352. DOI:10.2514/1.38562 |
| [3] | MUPPIDI S, TANG C Y, NORMAN J V, et al. Aerodynamic analysis of next generation supersonic decelerators[C]//32nd AIAA Applied Aerodynamics Conference, Atlandta, USA, 2014 |
| [4] | WACHI A, TAKAHASHI R, SAKAGAMI R, et al. Mars entry, descent, and landing by small THz spacecraft via membrane aeroshell[C]//AIAA SPACE and Astronautics Forum and Exposition, Orlando, USA, 2017 |
| [5] | REYNIER P, EVANS D. Post-flight analysis of IRDT blackout during earth reentry[C]//39th Plasmadynamics and Lasers Conference, Seattle, USA, 2008 |
| [6] | YAMADA K, NAGATA Y, ABE T, et al. Suborbital reentry demonstration of inflatable flare-type thin-membrane aeroshell using a sounding rocket[J]. Journal of Spacecraft and Rockets, 2015, 52(1): 275-284. DOI:10.2514/1.A32807 |
| [7] | GILBERT C, MAZOUE F, ORTEGA G, et al. New space application opportunities based on the inflatable reentry & descent technology[C]//AIAA/ICAS International Air and Space Symposium and Exposition: the Next 100 Years, Dayion, USA, 2003 |
| [8] |
吴杰, 张章, 候安平, 等. 充气式再入减速器动态气动载荷与结构特性研究[J]. 宇航学报, 2020, 41(3): 287-297.
WU Jie, ZHANG Zhang, HOU Anping, et al. Dynamic aerodynamic load and structural characteristics of inflatable reentry reducer[J]. Journal of Astronautics, 2020, 41(3): 287-297. (in Chinese) |
| [9] |
王帅, 余莉, 张章, 等. 气动热作用下的充气式减速器性能研究[J]. 航天返回与遥感, 2019, 40(2): 33-42.
WANG Shuai, YU Li, ZHANG Zhang, et al. Study on the performance of inflatable decelerator with aerodynamic heating[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(2): 33-42. (in Chinese) |
| [10] |
赵晓舜, 余莉, 杨雪. 不同迎角和速度下充气式返回舱气动性能预测[J]. 航天返回与遥感, 2016, 37(5): 27-36.
ZHAO Xiaoshun, YU Li, YANG Xue. The prediction of aerodynamic performance of inflatable reentry vehicle at various speeds and attack angles[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(5): 27-36. (in Chinese) |
| [11] | GUO J H, LIN G P, BU X Q, et al. Effect of static shape deformation on aerodynamics and aerothermodynamics of hypersonic inflatable aerodynamic decelerator[J]. Acta Astronautica, 2017, 136: 421-433. DOI:10.1016/j.actaastro.2017.03.019 |
| [12] | TAKAHASHI Y, HA D, OSHIMA N, et al. Aerodecelerator performance of flare-type membrane inflatable vehicle in suborbital reentry[J]. Journal of Spacecraft and Rockets, 2017, 54(5): 993-1004. DOI:10.2514/1.A33682 |
| [13] | MURMAN S M. Dynamic simulations of inflatable aerodynamic decelerator concepts[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Seattle, USA, 2009 |
| [14] |
万兵兵, 韩宇峰, 樊宇, 等. 高温空气传输特性对边界层稳定性及转捩预测的影响[J]. 航空动力学报, 2017, 32(1): 188-195.
WANG Bingbing, HAN Yufeng, FAN Yu, et al. Effect of transport properties of high temperature air on boundary layer stability and transition prediction[J]. Journal of Aerospace Power, 2017, 32(1): 188-195. (in Chinese) |
| [15] | TAKAHASHI Y, YAMADA K. Aerodynamic heating of inflatable aeroshell in orbital reentry[J]. Acta Astronautica, 2018, 152(1): 437-448. |
| [16] | ESCH D D, PIKE R W, ENGEL C D, et al. Stagnation region heating of a phenolic-nylon ablator during return from planetary missions[R]. NASA CR-112026, 1971 |
| [17] | BLOTTNER F G, JOHNSON M, ELLIS M. Chemically reaction viscous flow program for multicomponent gas mixture[R]. RR 70-754, 1972 |
| [18] | WILKE C R. A viscosity equation for gas mixturesf[J]. Journal of Chemical Physics, 1950, 18(4): 517-519. DOI:10.1063/1.1747673 |
| [19] | GUPTA R N, LEE K P, THOMPSON R A, et al. Calculations and curve fits of thermodynamic and transport properties for equilibrium air to 30 000 K[R]. NASA RP-1260, 1991 |
| [20] | PUGAZENTHI R S, KRISHNAN U. Design and performance analysis of a supersonic diffuser for plasma wind tunnel[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, 2008 |
| [21] | KIM K H, RHO O H, PARK C. Navier-Stokes computation of flows in arc heaters[J]. Journal of Thermophysics and Heat Transfer, 2012, 14(2): 250-258. |
| [22] | KIM K H, KIM C, RHO O H. Methods for the accurate computations of hypersonic flows: shock-aligned grid technique[J]. Journal of Computational Physics, 2001, 174(1): 81-119. DOI:10.1006/jcph.2001.6896 |
| [23] | MANABU M, TAKAHASHI Y, OBUYUKI O, et al. Aerodynamic heating prediction of an inflatable reentry vehicle in a hypersonic wind tunnel[C]//55th AIAA Aerospace Sciences Meeting, Grapevine, USA, 2017 |
| [24] | HANNEMANN K, SCHRAMM J M, Karl S, et al. Cylinder shock layer density profiles measured in high enthalpy flows in HEG[R]. AIAA-2002-2913 |
| [25] |
廖东骏, 柳森, 简和祥, 等. 高超声速球头激波脱体距离研究综述[J]. 实验流体力学, 2015, 29(6): 1-7.
LIAO Dongjun, LIU Sen, JIAN Hexiang, et al. Review of research on shock standoff distance for hypersonic sphere[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 1-7. (in Chinese) |
| [26] | INOUYE M. Shock standoff distance for equilibrium flow around hemispheres obtained from numerical calculations[J]. AIAA Journal, 1965, 3(1): 172-173. |
| [27] | 曹旭, 黄明星, 丁弘, 等. 充气式再入与减速系统柔性热防护材料的热冲击试验[J]. 载人航天, 2018, 24(1): 26-33. |
2. Laboratory of Aerospace Entry, Descent and Landing Technology, CASC, Beijing 100094, China