当前, 运载火箭子级的无损精确回收及可重复使用已经成为国际航天领域的研究热点。运载火箭子级回收的方式主要分为带翼飞回、垂直反推以及伞降回收3种。其中伞降回收方式主要有降落伞回收和翼伞回收2种[1]。相比于降落伞, 翼伞具有出色的滑翔性以及可操纵性, 是实现火箭子级回收的重要手段。这其中如何规划合理的翼伞回收航迹以实现子级的落点准确对保障地面人员的生命、财产安全及航天器的安全回收尤为重要。
基于翼伞进行火箭一子级回收主要采用径向归航、锥形归航和非比例控制等归航方式[2-3], 但这些归航方式存在如下问题: ①翼伞操纵比较频繁, 难以实现逆风着陆; ②接近目标点时容易造成翼伞频繁控制, 消耗能量过多; ③实现复杂, 且归航精度较低。当前, 分段归航策略成为翼伞航迹设计的主要方式[4]。国内外学者对分段归航做了很多研究, 如文献[5-6]将最优控制与分段归航相结合, 并且进行了仿真验证。文献[7-8]研究了翼伞的最优控制归航方案, 在分段归航的基础上考虑了地形威胁和风场的影响, 将航迹寻优问题转换成参数寻优问题, 应用粒子群算法实现了最优航迹规划等。
但上述研究未考虑翼伞不同转弯下偏量对火箭子级速度的影响, 且未将分段归航的盘旋削高圈数作为规划目标, 易导致翼伞控制机构能量过度消耗。此外, 粒子群算法计算耗时、迭代缓慢会降低航迹规划效率。为此, 本文针对某固体运载火箭一子级翼伞回收, 主要研究翼伞不同转弯下偏量对一子级速度及航迹的影响, 并提出一种基于天牛群算法的低能耗、高效率的翼伞一子级航迹规划算法。
1 火箭一子级翼伞组合体建模在翼伞航迹规划中可将翼伞和火箭一子级组合体视为刚体, 为更方便地分析翼伞运动对一子级及组合体姿态和航迹的影响, 本节首先根据火箭一子级和翼伞的动力学和运动学方程建立组合体的六自由度模型, 并分析翼伞在不同转弯半径下对组合体速度的影响。
1.1 假设条件为简化分析, 对翼伞建模做如下理想化假设:
1) 翼伞完全打开充满气后, 展开形状为固定的对称形(除去存在下拉量的情况);
2) 伞衣质心与压心重合, 位置在弦上距前缘1/4。
1.2 运动学和动力学方程表 1列出了某型火箭一子级翼伞组合体的主要气动系数, 其他参数请参考文献[9]中的具体数据。
翼伞一子级组合体运动学方程为
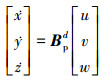
|
(1) |
式中: [x, y, z]表示大地坐标系内火箭一子级翼伞组合体的位置坐标; [u, v, w]分别为机体坐标系三轴方向上速度分量; Bpd表示为机体坐标系到大地坐标系的转换矩阵, 其表达式为

|
(2) |
式中, φ, θ, ψ分别表示组合体的滚转角、俯仰角和偏航角。
翼伞一子级组合体的动力学方程为
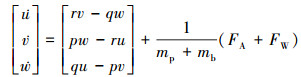
|
(3) |
式中: FA为气动力在组合体三轴上的分量; FW为重力在机体坐标系上的分量; [p, q, r]为机体坐标系中组合体的角速度; mp为翼伞的质量; mb为一子级的质量。
火箭一子级翼伞组合体的角运动方程为
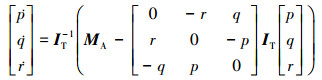
|
(4) |
式中: 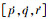
火箭一子级翼伞组合体的欧拉角变化率与机体坐标系的3个角速度分量之间的关系式可以写为
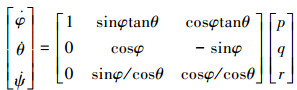
|
(5) |
火箭一子级翼伞组合体的航迹反映了组合体质点的运动轨迹, 航迹规划采用分阶段设计方式, 可体现出火箭一子级翼伞组合体的位置及航向角变化。因此, 本文首先通过火箭一子级翼伞组合体六自由度模型分析翼伞不同转弯下偏量对组合体速度及航迹的影响, 并在航迹规划中予以考虑。此外, 为降低翼伞航迹规划的复杂度, 进一步将六自由度模型简化为质点模型。
2.1 质点模型在风场方向水平、大小已知的情况下, 取大地坐标系, 水平风向为x轴方向, 按照右手准则确定y轴方向, z轴为垂直于地面向上, 则火箭一子级翼伞组合体的模型可以简化为
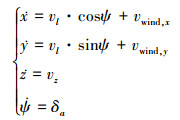
|
(6) |
式中:vl表示火箭一子级翼伞组合体的水平飞行速度;vz表示火箭一子级翼伞组合体的垂直下降速度;vwind, x表示水平风速在x轴的投影;vwind, y表示为水平风速在y轴的投影;ψ, 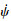
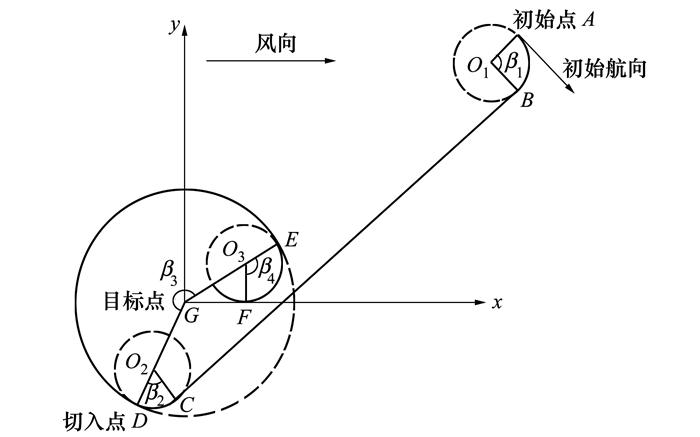
基于分段归航方案[10], 航迹分为飞行段、盘旋削高段和雀降段[11], 图 1为分段归航航迹示意图。
|
| 图 1 分段归航航迹示意图 |
其中BC段为飞行段, DE段为盘旋削高段, FG段为雀降段, AB、CD、EF段为圆弧过渡段, β1, β2分别表示圆弧过渡段弧度; β3表示盘旋阶段的圆弧段弧度; β4为盘旋削高段和雀降段之间的过渡段弧度, 是盘旋削高段末尾速度方向和逆风方向的夹角, 可通过调整β4确保雀降段能够逆风着陆。显然, 根据图 1可以很容易得出各段航迹的几何关系。
本文翼伞航迹规划的目标是确定盘旋削高段和雀降段切入点的最优坐标, 以保证组合体在雀降段能够逆风着陆于目标点, 同时能量消耗尽可能低。由于不同的盘旋半径对应不同的前向速度和垂直速度, 盘旋阶段的盘旋半径表达式为
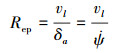
|
(7) |
式中,vl是关于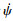
再以能量消耗最小以及落点偏差最小为优化目标, 首先构造如(8)式所示的函数
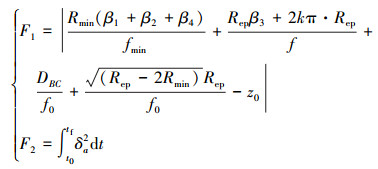
|
(8) |
式中:f0为组合体稳定滑翔状态下的滑翔比; fmin为组合体最小转弯半径时的滑翔比; f为组合体盘旋削高阶段时的滑翔比; 2kπ·Rep为盘旋阶段过程中盘旋段整圆周的水平距离; z0为翼伞开始工作时一子级高度。F1为组合体着陆时的偏差, 即设计的一子级航迹的垂直海拔高度与不同阶段下各水平飞行距离通过滑翔比转化成的高度总和之差的绝对值。DBC为BC段的直线长度。
取最终目标函数为
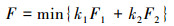
|
(9) |
本节中设定F1的权重系数为0.8, F2的权重系数为0.2。
2.3 天牛群算法本文采用天牛群算法[12-13]对(9)式所示的目标函数进行优化。
设有N只天牛, 分别表示为l=(l1, l2, …, lN), 每只天牛的位置可以定义为li=(Repi, θepi, ki)T, 也表示一个可能的函数最优解; 将其带入到设定的目标函数中, 得出每个天牛位置的适应度值; 完成该位置计算后, 天牛的位置会发生变化, 用vi=(vi1, vi2, vi3)T表示天牛位置变化时的速度, 速度更新表达式为

|
(10) |
式中: r1和r2为[0, 1]之间均匀分布的随机数;s=1, 2, 3;i=1, 2, ..N; pbesti=(pbesti1, pbesti2, pbesti3)T为当前个体的最优值, 并且将所有个体的最优解中的最小值作为全局最优解gbest=(gbest1, gbest2, gbest3)T;n表示当前正在进行的迭代次数, 学习因子c1, c2为常数, 惯性权重系数ω随过程变化, 变化规律为
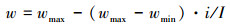
|
(11) |
I为最大迭代次数,天牛位置的更新规律为
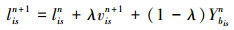
|
(12) |
(12) 式中的Ybisk表示由天牛2个触角探测到的信息强度决定的部分位移增量, 表达式为
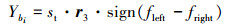
|
(13) |
式中,f(x)表示天牛位置的气味浓度, 也称为适应度函数, 其最大或最小值对应于气味源点, 代表所求目标函数。r3为[0, 1]之间均匀分布的随机数组成的1×3向量;根据天牛位置计算每个天牛的左侧距离xleft和适应度fleft及右侧距离xright和适应度fright
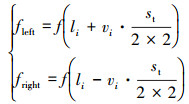
|
(14) |
对天牛的步长以及2个触角的质心之间的距离进行更新
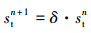
|
(15) |
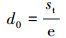
|
(16) |
(15) 式中δ为步长的衰减系数, d0为天牛两须之间的距离, e为自然常数。
基于天牛群算法对上述3个未知参数Rep, θep, k寻优的具体流程如图 2所示。

|
| 图 2 天牛群算法流程图 |
将寻优的结果代入到分段归航航迹中, 得出每段航迹起始点坐标, 计算出每个分段航迹的期望控制输入量(偏航角速率)、作用时间, 再结合(6)式得出归航航迹。
3 仿真实验 3.1 翼伞一子级组合体下偏量仿真结果已知翼伞一子级组合体转动惯量矩阵为

|
组合体总质量mp+mb为1 900 kg。假设组合体初始位置为(0, 0, 7 000)m, 初始速度为(10, 0, 40)m/s, 初始欧拉角为(-60°, 0°, 0°), 初始欧拉角速度为(0, 0, 0)(°)/s, 计算翼伞不同转弯下偏量的组合体前向速度和垂直速度, 并对前向速度、垂直速度与转弯下偏量进行拟合, 得出前向速度与转弯下偏量之间的数学关系式为
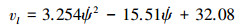
|
(17) |
垂直速度与转弯下偏量之间的数学关系式为

|
(18) |
设定目标落点为(-5 000, -4 000, 0)m, 最小转弯半径Rmin为100 m, 最小转弯半径时滑翔比为1.594, 算法寻优中的步长衰减系数δ为0.95, 盘旋阶段时的滑翔比为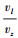
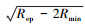
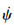
|
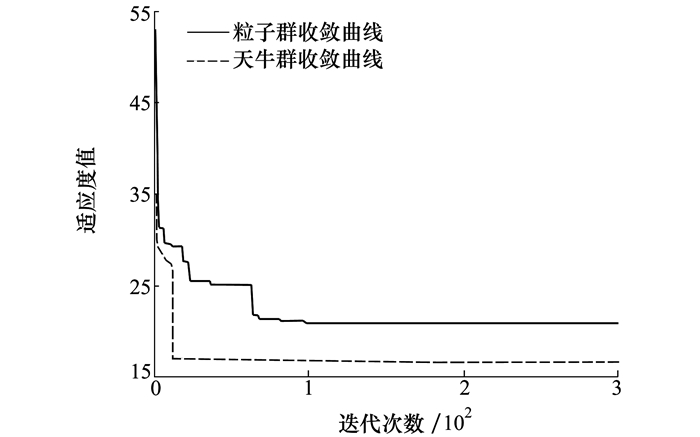
| 图 3 天牛群算法和粒子群算法收敛曲线 |
图 3给出了天牛群算法和粒子群算法的收敛性以及函数寻优结果。可以看出, 天牛群算法的收敛速度更快。此外通过多次算法寻优可知, 天牛群算法的最优值收敛于16.725左右, 而粒子群算法寻得的最优值在20.899左右。由此可见, 相对于粒子群算法, 天牛群算法由于在寻优过程中加入了天牛粒子自身的判断, 从而降低了陷入局部最优的概率, 同时收敛速度更快, 寻优结果更好。
通过天牛群算法得到(9)式中的目标函数最优值为0.317 3, 其对应的3个参数最优值为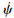

|
| 图 4 右侧下偏规划航迹 |
由图 4a)可得, 最终航迹规划的落点为(-489 9, -401 7, 0.316 1)m, 距离目标落点偏差为102.42 m。从期望转弯下偏量的变化曲线中可以看出, 组合体的盘旋削高段期望转弯下偏量为-0.039 9, 转弯半径为788.63 m。根据控制量曲线可以算出归航的总能量消耗为1.587 5。
左侧下偏与右侧下偏的航迹结果如图 5所示。
|
| 图 5 不同下偏方式规划航迹 |
由图 5可知, 无论是左侧下偏的逆时针转弯运动还是右侧下偏的顺时针转弯运动, 规划的航迹都能准确到达目标点。
对不同转弯方法的落点偏差以及能量消耗统计结果如表 2所示。可以看出, 两者规划落点偏差仅10 m, 但能量消耗相差较大, 这是因为目标点在初始飞行方向的右侧, 左侧转弯时需要以最小转弯半径左转更大的角度, 期望单侧转弯控制量作用时间长, 所以理论上应根据初始飞行方向和目标点决定采用的转弯方式, 目标点在初始飞行方向左侧时选择左侧转弯, 在右侧时选择右侧转弯。
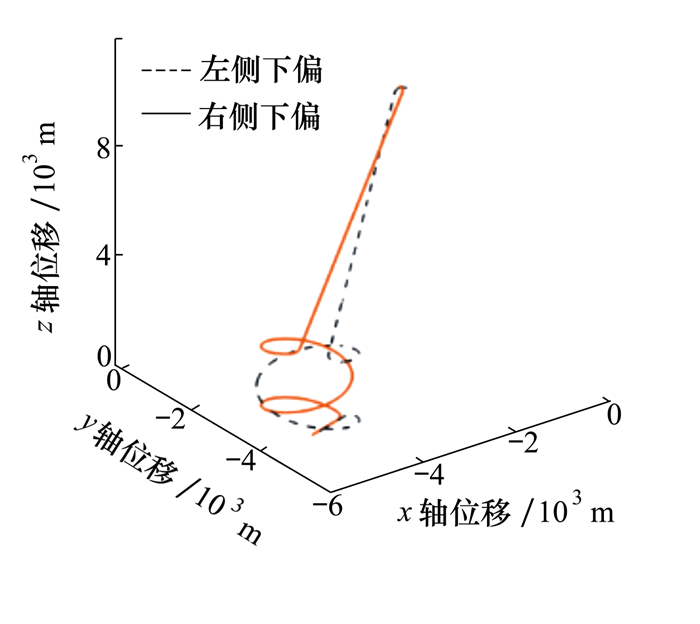
火箭一子级翼伞归航航迹若在持续沿x轴正向常值风情况下, 会因为逆风导致到达目标点的时间延长, 进一步造成最终落点偏差位置较大, 为解决这一问题, 本文将平均风的影响在航迹规划中予以考虑, 方法是在持续沿x轴正向常值风情况下, 调整无风情况下规划落点的位置, 使该落点叠加水平风场产生的位移刚好等于任务要求落点。在沿x轴正向平均风速为5 m/s的常值风下, 原目标点设置为(-5 000, -4 000, 0)m, 补偿风场引起的距离偏差后, 规划目标点修正为(-7 606, -4 000, 0)m, 天牛群算法对该目标点进行寻优, 得出其中的最优参数为, 
|
| 图 6 常值风下的分段归航航迹 |
由图 6可知, 最终规划落点坐标为(-4 992, 4 003, -1.404)m, 速度为(-24.47, 0, 10.7)m/s火箭一子级翼伞组合体的雀降段方向为x轴负向, 为逆风雀降, 满足要求。
4 结论本文通过翼伞和火箭一子级组合体的六自由度模型仿真得到翼伞转弯下偏量对前向速度、垂直速度的影响并拟合出数学关系加入到航迹规划的过程中, 可以使各航迹段更贴近于高保真模型的飞行速度, 减少后续的航迹跟踪控制的难度; 采用天牛须算法进行航迹规划的参数寻优, 相较于粒子群算法寻优速度更快, 并且优化了粒子群算法容易陷入局部最优的缺点; 在考虑能量最优的同时, 将盘旋削高的圈数作为寻优目标之一, 仿真结果表明该航迹规划算法能够在风场影响下规划出落点精准的火箭一子级回收航迹。
| [1] | CHEN Q, ZHAO M, LI Y H, et al. Optimal segmented path planning for parafoil system based on gradient descent method[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(12): 324226. |
| [2] | GOODRICK T F. Estimation of wind effect on gliding parachute cargo systems using computer simulation[R]. AIAA-1970-1193 |
| [3] | GOODRICK T F, MURPHY A L J, et al. Analysis of various automatic homing techniques for gliding airdrip systems with comparative performance in adverse winds[R]. AIAA-1973-0462 |
| [4] | KLOTZ H, MARKUS M. Guidance and control for autonomous reentry and precision landing of a small capsule[C]//Spacecraft Guidance, Navigation and Control Systems, 2000 |
| [5] | KAMINER I I, YAKIMENKO O A. On the development of GNC algorithm for a high-glide payload delivery system[C]//42nd IEEE International Conference on Decision and Control, 2003 |
| [6] |
熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科技大学, 2005 XIONG Jing. Researth on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005 (in Chinese) |
| [7] |
谢亚荣, 吴庆宪, 姜长生, 等. 粒子群算法在翼伞空投系统航迹规划中的应用[J]. 航空兵器, 2010(5): 7-10.
XIE Yarong, WU Qingxian, JIANG Changsheng, et al. Application of particle swarm optimization algorithm in route planning for parafoil airdop system[J]. Aero Weaponry, 2010(5): 7-10. (in Chinese) |
| [8] |
陶金. 复杂环境下翼伞系统的建模与归航控制研究[D]. 天津: 南开大学, 2017 TAO Jin. Research on modeling and homing control of parafoil systems in complex environments[D]. Tanjin: Nankai University, 2017 (in Chinese) |
| [9] |
郭一鸣, 闫建国, 邢小军, 等. 变形翼伞回收系统的建模与分析[J]. 西北工业大学学报, 2020, 38(5): 952-958.
GUO Yiming, YAN Jianguo, XING Xiaojun, et al. Modeling and analysis of deformed parafoil recovery system[J]. Journal of Northwestern Polytechnical University, 2020, 38(5): 952-958. (in Chinese) DOI:10.3969/j.issn.1000-2758.2020.05.005 |
| [10] | JANN T. Aerodynamic model identification and GNC design for the parafoil-load system ALEX[C]//16th AIAA Aerodynamic Decelerator Systems Technology Conferencea and Seminar, 2001 |
| [11] | SOPPA U, STRAUCH H, GOERIG L, et al. GNC concept for automated landing of a large parafoil[C]//14th Aerodynamic Decelerator Systems Technology Conference, 1997 |
| [12] | JIANG X, LI S. Beetle antennae search without parameter tuning(BAS-WPT) for multi-objective optimization[J]. Filomat, 2020, 34(15): 5113-5119. DOI:10.2298/FIL2015113J |
| [13] | WANG T, YANG L, LIU Q. Beetle swarm optimization algorithm: theory and application[J]. Filomat, 2020, 34(15): 5121-5137. DOI:10.2298/FIL2015121W |



