2. 中国飞机强度研究所, 陕西 西安 710065
高超声速飞行器是未来飞行器发展的重要方向之一, 也是目前的研究热点问题[1]。由于严重的气动加热现象, 高超声速飞行器必须承受极大的热载荷和气动载荷, 这对热防护技术提出了更高的要求[2]。传统的热防护结构并不承担机身结构载荷, 但随着可重复使用高超声速飞行器对结构效率要求的提高, 承载/防热一体化将是未来热防护结构的主要形式[3], 而点阵结构正好可以满足这一设计需求。
以桁架杆件为芯子的点阵结构, 比刚度和比强度大、抗冲击性能好[4], 具有很强的面外承载能力、高孔隙率和芯子表面积, 可以实现强制对流换热[5], 是一种兼具承载与防热性能的优良结构。此外, 点阵结构可设计性强, 可以根据不同内部芯子设计成四面体点阵[6]、金字塔点阵[7]、X型点阵[8]、Kagome点阵[9]等。目前对单级点阵结构的研究已有很多, Zhang等[8]对X型点阵的面外压缩、面内剪切和三点弯曲性能进行了理论计算与数值仿真, 发现更厚的芯子具有更大的屈服强度, 且剪切强度与芯子方向密切相关。Wang等[10]对碳纤维热塑性点阵夹芯结构进行了研究, 发现芯子角度对结构承载性能有很大的影响, 面外受载下失效模式包括基体断裂、欧拉屈曲、纤维剥离。Yang等[5]对四面体型和Kagome型点阵进行了对流换热试验, 发现Kagome型由于内部结点会引发更为复杂的流动, 其换热性能好于四面体型, 且结构不同方向的换热效率不同。Li等[11]研究了复合材料金字塔点阵夹芯板在真空热循环后的压缩和剪切性能, 结果表明失效模式受真空热循环次数的影响较大。Wang等[12]研究了金属蜂窝结构受面外压缩载荷时的热力耦合性能, 表明结构最大应力和吸能特性随温度升高而降低, 且破坏载荷效率和变形模式对温度变化不敏感。
Kooistra[13]在单级点阵结构的基础上, 首次提出了多级点阵结构, 即在原来单级芯子内部引入二级芯子, 发现多级点阵结构的力学性能相比单级结构有很大程度提高。之后许多学者逐渐开展了关于多级点阵的研究, Fan等[14]研究了金字塔-蜂窝多级点阵结构的力学性能, 发现这种结构能以尽可能轻的质量实现更高的承载。Qi等[7]研究了单层和多层金字塔点阵结构的力学性能, 结果表明恒定横截面芯子的断裂强度更低, 且多层级结构具有更强的承载能力。Yin等[15]对金字塔-金字塔多级复合材料点阵结构的压缩性能进行研究, 发现芯子杆件的长度比很大程度上影响结构的承载效率, 且二级中空芯子能很大程度上对结构进行优化。Wu等[16-17]设计了金字塔多级点阵结构, 并对其承载性能进行了理论预测与试验验证, 发现多级结构的承压性能是同等一级结构的4倍, 且金字塔-金字塔结构性能更好。
综合上述研究可以看出, 目前针对点阵结构的研究主要集中在常温环境下, 对于高温环境下结构热力耦合性能的研究相对较少。本文以高超声速飞行器背风面(约350℃)热防护结构为应用前景, 分别对Kagome点阵和2种金字塔钛合金点阵结构在25℃和350℃环境下的面外压缩性能进行试验和数值模拟研究, 通过考虑温度载荷下结构的承载能力来研究其热力耦合性能, 揭示结构损伤失效机理, 为推动其工程化应用提供支持。
1 试验 1.1 试验件设计与制备针对不同构型点阵结构的承载/防热一体化能力, 开展试验件设计、制备与试验测试。已有研究表明, 点阵结构的防热能力随其内部芯子表面积增加而增强[5]、多级点阵的承载能力相比单级点阵有很大程度的提升[17], 且金字塔点阵相对其他形式点阵有更强的可设计性。基于此, 分别设计Kagome型(K-1)、单级金字塔型(single-stage pyramidal, SP)和多级金字塔型(multistage pyramidal, MP)3类点阵结构单胞, 其中SP型和MP型结构重量相同; 然后对Kagome单胞进行阵列得到2胞元(K-2)、3胞元(K-3)、12胞元(K-12)的构型, 以研究胞元数目及边界条件对结构承载能力的影响。采用3D打印技术完成试验件制备, 其微观组织更为细小, 致密性好于传统工艺。每种类型4件(25℃和350℃环境下各2件), 材料为TC4钛合金, 几种点阵结构形式及几何参数示意如图 1~2所示。
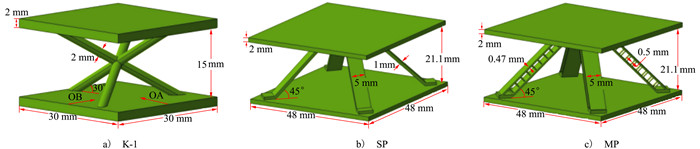
|
| 图 1 3种点阵单胞示意图 |
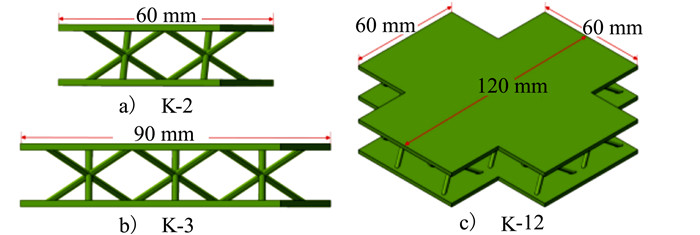
|
| 图 2 Kagome点阵多胞元示意图 |
分别对上述几种结构试验件进行25℃和350℃环境下的面外压缩试验, 试验根据标准ASTM C365/C365M-16进行, 设备为INSTRON-5940万能试验机(最大载荷100 kN, 精度0.5级, 位移测量精度0.2 μm), 350℃在高温炉下进行(高温炉最高温度400℃, 温度精度0.1℃), 温升速率3℃/min, 升温至350℃时停止升温并保温30 min, 以保证试验件在炉内受热均匀, 之后对试验件进行压缩试验。试验加载速率0.5 mm/min, 对试样进行预加载消除压头与试样之间的明显间距, 同时观察机器载荷位移示数以及位移-载荷曲线是否正常, 采用平行仪满足上下平行度要求。试验件加载示意如图 3所示。

|
| 图 3 试验件加载示意图 |
在CATIA中建立几何模型, 尺寸与图 1保持一致, 并整体导入ABAQUS有限元分析软件。根据不同结构特点划分网格, 面板及金字塔结构选择C3D8R单元以提高计算精度[18], Kagome芯子结点处六面体网格划分困难, 故选择C3D10单元, 芯子与面板连接处适当增加布种数以提高计算精度, 3种单胞有限元模型如图 4所示, 网格数分别为17 465, 16 166, 38 610。

|
| 图 4 3种单胞有限元模型示意图 |
分析过程中, 下面板固支, 上面板施加载荷模拟面外压缩过程。首先进行线性特征值分析, 在ABAQUS中选择分析类型为线性摄动-屈曲, 得到结构的一阶屈曲模态和临界屈曲载荷, 然后考虑材料非线性、引入初始缺陷, 选择分析类型为静态-Riks[19-20], 对结构进行非线性屈曲分析, 上面板与参考点施加方程约束, 进行位移加载。TC4钛合金弹性模量112 GPa, 泊松比0.34;350℃环境以Johnson-Cook(J-C)模型作为材料本构, 其在考虑温度软化、不考虑应变率时的表达式如(1)式所示[21]
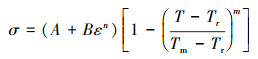
|
(1) |
式中: σ, ε分别为等效应力、等效塑性应变; A为初始屈服应力; B为应变硬化系数; T, Tr, Tm分别为试验温度、室温、融化温度。参考相关文献[22-23]中基于传统工艺制造的TC4合金相关材料系数及热物性参数, 如表 1~2所示。
以加载过程中的最大载荷作为结构的极限载荷, 3类结构的试验测试与数值仿真得到的极限载荷如表 3所示。由表中数据可知, 由于高温对TC4材料的软化作用, 350℃环境下极限载荷相比25℃都有所减小, 整体而言, 数值仿真结果与试验值吻合较好, 验证了数值方法的可靠性。
| 结构形式 | 温度/℃ | 试验值/kN | 仿真值/kN | 误差/% |
| K-1 | 25 | 3.85 | 3.90 | 1.30 |
| 350 | 2.71 | 2.84 | 4.80 | |
| K-2 | 25 | 8.26 | 7.83 | -5.49 |
| 350 | 5.31 | 5.67 | 6.78 | |
| K-3 | 25 | 11.57 | 11.98 | 3.54 |
| 350 | 7.93 | 8.60 | 8.45 | |
| K-12 | 25 | 49.34 | 48.74 | -1.22 |
| 350 | 32.16 | 35.03 | 8.92 | |
| SP | 25 | 10.57 | 11.34 | 7.28 |
| 350 | 7.47 | 8.24 | 10.31 | |
| MP | 25 | 12.51 | 11.76 | -5.60 |
| 350 | 9.19 | 9.85 | 7.18 |
不同胞元数目Kagome结构的载荷-位移曲线如图 5a)所示, 极限载荷如图 5b)所示。由载荷-位移曲线可以看出: 在加载初始阶段, 面外位移随压缩载荷线性增加; 在接近极限载荷时斜率逐渐减小; 到极限载荷之后, 面外载荷缓慢减小, 但位移增大较为明显, 结构逐渐失稳并进入一段较长的吸能过程, 直至发生完全失效。同时, 随着胞元数目的增加, 结构面外承压的强度和刚度逐渐增加; 由于4种构型到达最大载荷的面外位移值基本一致, 因此刚度的增加是线性的。根据图 5b)可以看出, 在25℃和350℃下, 极限载荷随胞元数目的增加也呈线性趋势。由此可见, 多胞元数目的结构承载能力是对应n个单胞的线性累积, 因此对于结构单胞的研究可以代表结构形式的面外承载性能, 采用单胞元代替多胞元开展相关研究是合理的。
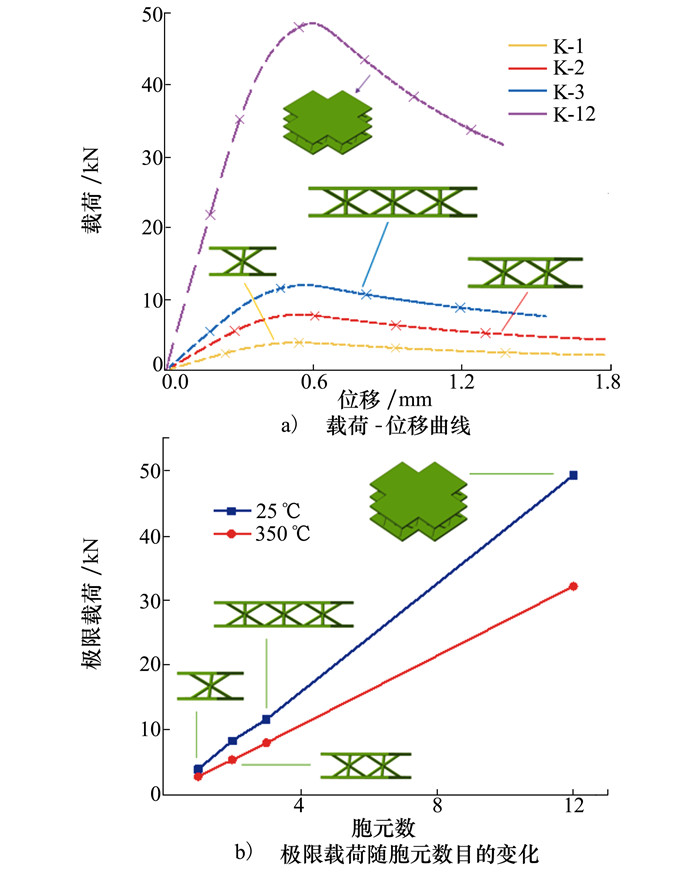
|
| 图 5 不同胞元数目Kagome结构的承载性能 |
首先对点阵单胞350℃下受面外压缩载荷进行线性特征值分析, 得到其一阶屈曲模态和临界屈曲载荷。基于线性特征值分析的3种点阵单胞一阶屈曲模态如图 6所示。可以看出, Kagome单胞由于上下部分关于结点对称, 受载时上面部分发生扭曲、下面部分3个杆件都发生屈曲; SP型单级金字塔点阵的2个芯子发生屈曲且程度不一致; MP型多级金字塔点阵只有一个芯子发生屈曲, 且内部二级支柱芯子出现较大应力集中。

|
| 图 6 3种点阵单胞面外受载的一阶屈曲模态 |
然后以一阶屈曲模态的2%作为初始缺陷[21], 考虑结构大变形, 进行Riks方法非线性屈曲分析。从承受极限载荷开始, 整个屈曲过程中3种单胞形式几个典型状态的应力云图如图 7~9所示。图中U为面外位移, 每组中第一个云图为结构极限载荷对应的应力分布。对比3种单胞可以看出, MP型多级金字塔构型的刚度要大于另外2种单级构型, 主要是因为二级芯子的存在提高了结构抵抗变形的能力。

|
| 图 7 Kagome单胞350℃面外受载过程非线性屈曲分析应力云图 |

|
| 图 8 SP型单级金字塔单胞350℃面外受载过程非线性屈曲分析应力云图 |

|
| 图 9 MP型多级金字塔单胞350℃面外受载过程非线性屈曲分析应力云图 |
Kagome点阵单胞在面外位移0.42 mm时达到极限载荷, 结构未见明显失效, 除中间结点处应力较大外, 其余部分结构应力水平普遍较低; 继续受载至0.6 mm时, 沿结点上下中心对称处的芯子部位已发生明显应力集中, 此时结构承载已逐渐下降; 面外位移至0.9 mm时, 应力集中部位继续增大, 且出现明显可见的屈曲失效; 继续压缩, 3个芯子屈曲更加严重, 结构逐渐失去承载能力。
SP型单级点阵单胞在受载时, 由上下面板处逐渐向中间芯子传递载荷, 在面外位移0.18 mm时已经达极限载荷; 加载至0.2 mm时, 2个芯子中间出现应力集中并发生局部屈曲, 另外2个芯子整体应力水平较小; 继续加载, 应力集中现象更加严重, 最终由于2个芯子发生严重屈曲而使结构失去承载能力。
MP型多级点阵单胞极限载荷大于SP型, 但在承受极限载荷时面外位移为0.16 mm, 小于SP型, 因此相比同等质量的SP型单级结构, 其面外承载刚度有所增强; 之后继续加载, 面外位移变化十分缓慢, 而对应结构应力分布形式变化较大, 逐渐进入由局部失效到整体失效的变化阶段, 最终由4个一级芯子应力分布一致逐渐变为其中2个一级芯子的严重屈曲, 之后面外位移才有明显变化。屈曲过程最后阶段,发生屈曲一级芯子内部的二级芯子应力逐渐增大, 最终使结构逐渐失效。
3.4 不同层级影响规律比较2种金字塔点阵单胞的面外压缩极限载荷及其内部芯子换热表面积大小如表 4所示。面外极限载荷反映结构的承载能力, 内部芯子换热表面积反映了结构的对流换热能力。
| 单胞类型 | 温度/℃ | 极限载荷/kN | 芯子换热表面积/mm2 |
| SP | 25 | 10.57 | 1 547 |
| 350 | 7.47 | ||
| MP | 25 | 12.51 | 3 588 |
| 350 | 9.19 |
可以看出, MP型的芯子表面积相对SP型增加131.9%, 较大的芯子表面积可以增强金属与空气间的换热[5], 因此其防热能力要很大程度上强于SP型结构。同时, 在常温环境下, MP型的极限载荷相对SP型结构增加18.4%;而在350℃环境下, MP型的极限载荷相对SP型结构增加23.0%。可见, MP型多级金字塔结构不仅有良好的对流换热能力, 而且由于内部存在支柱杆件组成的“次级结构”, 在面外受载时, 二级芯子可以通过吸收能量延缓结构发生屈曲, 故其承载能力相对SP型单级结构有很大程度的提高。此外, 在高温环境下由于芯子表面积的增大会一定程度上减小局部热应力, 从而减小高温对结构承载的影响, 因此350℃下MP型结构承载能力相对SP型结构提升比25℃下更为明显。
3.5 温度影响规律研究3种点阵单胞在25℃和350℃环境下的失效形式如表 5所示, 由表可见, 在研究的温度范围内, 温度对结构的失效形式并无明显影响。SP型和MP型结构变形方向与仿真结果略有差异, 这是由于芯子往内和往外屈曲具有随机性, 加工过程中的极小缺陷也会影响最终的变形方向, 因此可以认为仿真结果与试验结果具有较好的一致性。Kagome点阵单胞失效形式为3个支撑杆件都发生屈曲, 且沿结点上下失效呈中心对称; SP型点阵单胞的4个芯子中有单侧2个发生屈曲, 另外2个芯子未发生明显屈曲; MP型多级点阵单胞的一级芯子与SP型屈曲形式类似, 但在一级芯子屈曲部位的二级支柱芯子与一级芯子连接处发生断裂, 说明二级芯子的存在为结构承载性能的提高起了重要作用。
尽管高温对结构失效形式无明显影响, 但由于高温对金属材料的软化作用, 3种单胞在350℃环境下面外承载能力都有所降低, 如图 10所示。其中Kagome点阵单胞极限载荷下降29.6%, SP型单胞极限载荷下降29.3%, MP型单胞极限载荷下降26.5%。可见, 高温对2种单级构型的影响程度基本一致, 但对多级构型的影响明显减小, 因此多级构型有更好地承载/防热一体化性能。
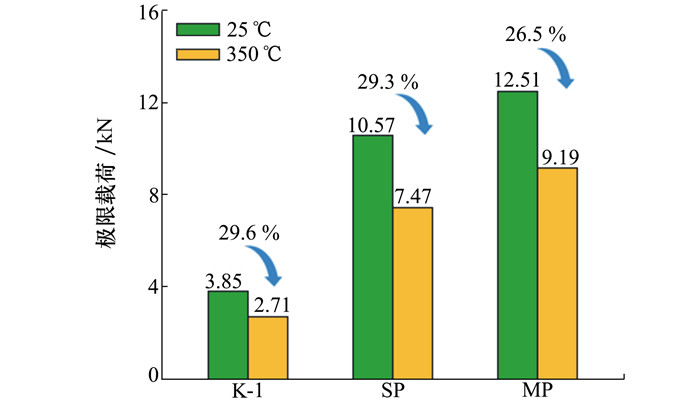
|
| 图 10 高温对结构承载能力的影响 |
本文设计并基于3D打印技术制造了TC4合金Kagome结构不同胞元数目的点阵构型、单级金字塔点阵单胞和多级金字塔点阵单胞, 采用试验与数值模拟的方法研究3种点阵结构在25℃和350℃环境下的面外承载能力与失效形式, 得出以下结论:
1) 采用的Riks后屈曲分析方法, 能准确模拟钛合金点阵结构芯子发生屈曲失效的过程, 数值仿真结果与试验值吻合程度较好;
2) 钛合金多胞元点阵结构的强度和刚度均是对应n个单胞的线性累积, 说明采用单胞元研究多胞元承载能力的方法是合理的;
3) 3种钛合金点阵单胞在受面外压缩载荷时, 失效形式均为芯子发生屈曲。其中Kagome单胞3个芯子均发生屈曲; 金字塔单级点阵一侧的2个芯子发生屈曲; 金字塔多级点阵一侧2个芯子发生屈曲且屈曲部位的二级芯子应力较大, 二级芯子对结构承载做了很大贡献;
4) 在研究的温度范围内, 高温对钛合金点阵结构的失效形式无明显影响, 但会降低结构的承载能力。多级点阵构型由于内部芯子表面积的增大, 承载能力受温度影响小于Kagome构型和单级金字塔构型;
5) 相对同等重量的单级点阵, 多级点阵结构内部换热表面积大、承载能力强, 且在高温环境下, 多级点阵的承载性能优势更为明显, 表明多级点阵是一种承载/防热一体化的优良结构。
| [1] |
廖孟豪. 2018年度国外高超声速飞行器发展动向[J]. 飞航导弹, 2019(3): 1-4.
LIAO Menghao. Development trend of foreign hypersonic vehicles in 2018[J]. Flying Missile, 2019(3): 1-4. (in Chinese) |
| [2] | CHEN Fang, LIU Hong, ZHANG Shengtao. Time-adaptive loosely coupled analysis on fluid-thermal-structural behaviors of hypersonic wing structures under sustained aeroheating[J]. Aerospace Science and Technology, 2018, 78: 620-636. DOI:10.1016/j.ast.2018.05.015 |
| [3] |
徐世南, 吴催生. 高超声速飞行器热防护结构研究进展[J]. 飞航导弹, 2019(4): 48-55.
XU Shinan, WU Cuisheng. Research progress of hypersonic vehicle thermal protection structure[J]. Flying Missile, 2019(4): 48-55. (in Chinese) |
| [4] | SCHAEDLER T A, JACOBSEN A J, TORRENTS A, et al. Ultralight metallic microlattices[J]. Science, 2011, 334(6058): 962-965. DOI:10.1126/science.1211649 |
| [5] | YANG Guangmeng, HOU Chi, ZHAO Meiying, et al. Comparison of convective heat transfer for Kagome and tetrahedral truss-cored lattice sandwich panels[J]. Scientific Reports, 2019, 9(11): 3731. |
| [6] | ZHANG Guoqi, MA Li, WANG Bing, et al. Mechanical behaviour of CFRP sandwich structures with tetrahedral lattice truss cores[J]. Composites Part B, 2012, 43(2): 471-476. DOI:10.1016/j.compositesb.2011.11.017 |
| [7] | QI Ge, JI Bin, MA Li. Mechanical response of pyramidal lattice truss core sandwich structures by additive manufacturing[J]. Mechanics of Advanced Materials and Structures, 2019, 26(15): 1298-1306. DOI:10.1080/15376494.2018.1432805 |
| [8] | ZHANG Qian, JIANG Wenchun, ZHANG Yanting, et al. shear and bending performance of X-type lattice truss panel structure by theoretical method and simulation[J]. International Journal of Steel Structures, 2020(20): 259-271. |
| [9] | HOU Chi, YANG Guangmeng, WAN Xiaopeng, et al. Study of thermo-fluidic characteristics for geometric-anisotropy Kagome truss-cored lattice[J]. Chinese Journal of Aeronautics, 2019, 32(7): 1633-1645. |
| [10] | WANG Zhenwei, LUAN Congcong, LIAO Guangxin, et al. Mechanical and self-monitoring behaviors of 3D printing smart continuous carbon fiber-thermoplastic lattice truss sandwich structure[J]. Composites Part B, 2019, 176: 107215. DOI:10.1016/j.compositesb.2019.107215 |
| [11] | LI Xiaodong, WU Linzhi, MA Li, et al. Compression and shear response of carbon fiber composite sandwich panels with pyramidal truss cores after thermal exposure[J]. Mechanics of Advanced Materials and Structures, 2019, 26(10): 866-877. DOI:10.1080/15376494.2018.1430269 |
| [12] | WANG Shubin, LI Weiguo, TAO Yong, et al. Investigation on the temperature dependent out-of-plane quasi-static compressive behavior of metallic honeycombs[J]. Thin-Walled Structures, 2020, 149: 166625. |
| [13] | KOOISTRA Gregory W, DESHPANDE Vikram, WADLEY Haydn N G. Hierarchical corrugated core sandwich panel concepts[J]. Journal of Applied Mechanics, 2007, 74(2): 259-268. DOI:10.1115/1.2198243 |
| [14] | FAN Hualin, QU Zhanxin, XIA Zhicheng, et al. Designing and compression behaviors of ductile hierarchical pyramidal lattice composites[J]. Materials & Design, 2014, 58: 363-367. |
| [15] | YIN Sha, WU Linzhi, NUTT Steven R. Compressive efficiency of stretch-stretch-hybrid hierarchical composite lattice cores[J]. Materials & Design(1980-2015), 2014, 56: 731-739. |
| [16] | WU Qianqian, VAZIRI Ashkan, ASL Mohamad Eydani, et al. Lattice materials with pyramidal hierarchy: systematic analysis and three dimensional failure mechanism maps[J]. Journal of the Mechanics and Physics of Solids, 2019, 125: 112-144. DOI:10.1016/j.jmps.2018.12.006 |
| [17] | WU Qianqian, GAO Ying, WEI Xingyu, et al. Mechanical properties and failure mechanisms of sandwich panels with ultra-lightweight three-dimensional hierarchical lattice cores[J]. International Journal of Solids and Structures, 2018, 132/133: 171-187. DOI:10.1016/j.ijsolstr.2017.09.024 |
| [18] | ZHANG Zhong, LEI Hongshuai, XU Mengchuan, et al. Out-of-plane compressive performance and energy absorption of multi-layer graded sinusoidal corrugated sandwich panels[J]. Materials & Design, 2019, 178: 107858. |
| [19] |
马良, 马玉娥, 秦强. 热力耦合下不同加筋壁板稳定性分析[J]. 西北工业大学学报, 2020, 38(1): 40-47.
MA Liang, MA Yu'e, QIN Qiang. Stability analysis of different stiffened plates in thermal-mechanical coupling environments[J]. Journal of Northwestern Polytechnical University, 2020, 38(1): 40-47. (in Chinese) |
| [20] |
赵佳音. Riks弧长法在压杆非线性屈曲分析中的应用[J]. 船舶标准化工程师, 2021, 54(1): 67-70.
ZHAO Jiayin. Application of Riks arc length method in non-linear buckling analysis of compressive rods[J]. Ship Standardization Engineer, 2021, 54(1): 67-70. (in Chinese) |
| [21] | REN Junxue, CAI Ju, ZHOU Jinhua, et al. Inverse determination of improved constitutive equation for cutting titanium alloy Ti-6Al-4V based on finite element analysis[J]. The International Journal of Advanced Manufacturing Technology, 2018, 97(9/10/11/12): 3671-3682. |
| [22] |
刘旭阳. TC4钛合金动态本构关系研究[D]. 南京: 南京航空航天大学, 2010 LIU Xuyang. Research on dynamic constitutive relationship of TC4 titanium alloy[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese) |
| [23] | 《ChinaAviation Materials Handbook》Editorial Committee. China aviation materials handbook: volume Ⅳ, titanium alloys and copper alloys[M]. Beijing: China Standard Press, 2001: 104-131. |
2. Aircraft Strength Research Institute of China, Xi′an 710065, China










