2. 陕西省飞行控制与仿真技术重点实验室, 陕西 西安 710129
飞行空战研究一直以来都是飞行控制领域的重点难点,并且空战的研究方法也在不断地改进。早期的空战决策研究中,大多数采用博弈论、最优控制等思想。Jarmark[1-2]建立双机对抗微分博弈模型,然后使用微分动态规划法来求解。Imado等[3]使用了最优控制方法,通过对迎角和推力的控制实现空战中对导弹的规避。这些方法的主要思路都是首先建立理想的空中对抗模型,然后使用一些数学方法,比如微分动态规划法来得到最优解,而实际的空战模型非常复杂,加上这一时期的研究中几乎没有建立态势模型,因此优化目标通常是飞机的状态信息,得出的最优解的应用范围比较小。
为解决这种方法的不足,关于空战的架构研究开始发展起来。Byrnes[4]提出了一种概念无人机FQ-X,这种无人机采用了观察、判断、决策、执行回路(observation, orientation, decision, action, OODA)和能量机动结构,并在OODA的框架下设计了无人机自主作战决策。李清伟等[5]提出了一种空战分层决策模型,使用经验知识将复杂高维的战场决策分解成数个低维的模块,决策模型更加符合空战作战经验。OODA作为这一时期的空战架构,给众多研究者指明了空战中的研究重点和研究方向,其中态势评估可以作为OODA的评价标准也成为研究重点。
态势评估作为空战博弈的感知和评价[6]在空战决策模型中起到至关重要的作用。在众多的态势评估研究成果中,几乎都是基于导弹攻击区进行设计的,其中角度态势尤为重要。史振庆等[7]在估计角度态势时,考虑了敌机的攻击区对我机的影响。兰轶冰等[8]使用几何学方法对角度态势进行评估。王光辉等[9]使用区间数和模糊综合评判结合的方法得到空战威胁评估模型。赵克新等[10]使用改进的决策树方法估计空战态势。Xuan等[11]使用灰色模糊贝叶斯网络表示空战态势。姜龙亭等[12]根据贝叶斯概率提出一种动态变权重的态势评估方法。此外,态势评估还可以应用在强化学习的奖惩函数上,以强化学习为基础的空战策略也流行开来。
近年来,随着计算机算力的提升,信息化、人工智能等技术的发展,深度学习、强化学习等人工智能计数的研究流行开来,而基于这种人工智能思路的空战决策的研究也已有不少。谢建峰等[13]使用强化学习的思想对遗传算法进行改进,设计了无人机空战机动决策算法。谢俊洁等[14]在空战决策中使用Q-learning的强化学习方法进行目标分配,使用智能优化算法进行火力分配。Lowe等[15]使用了actor-critic方法的强化学习研究了多智体的协同对抗问题。2020年DARPA举行了阿尔法狗斗试验,表明了空战决策技术日益成熟,且愈加得到重视。
空战研究不仅体现在顶层的空战决策上,而且在底层的控制研究也有不少,蓝伟华等[16]根据不同空战环境设计了瞄准攻击、逃逸等控制律。刘佩等[17]采用复合控制思想,在原始控制中加入限幅、指令淡化等功能,来实现空战机动的飞行轨迹控制。反步法作为一种成熟的非线性控制方法已经应用于各类控制领域上。反步法是在20世纪90年代初,由Kanellakopoulos等提出,该方法在设计之处就考虑了Lyapunov稳定性,通过引入虚拟控制的概念,采用逐步反推的思想对每一环进行控制器设计。反步法发展至今,有着诸多的改进,其中约束反步法能够有效解决常规反步法没有考虑系统输入和状态的约束问题。在设计约束反步法控制器中,一种方案是引入误差的修正量,通过对修正量的更新,保证系统稳定;另一种方案是引入障碍Lyapunov函数,由此设计的控制器会在范围的边界附近阻止状态越界。反步法作为目前非线性控制中较为成熟的方法,在飞行控制方面有着诸多研究。
针对飞行机动过程中没有考虑态势信息,导致己机在机动时飞行安全受到影响的问题,比如飞机执行一个斤斗等类似的机动,整个机动做完耗费的时间基本上都超过20 s,有人机由于过载限制,所用时间会更长,而在这段时间内,己机的路径都是固定的,很容易被预测并针对。本文提出了带态势信息约束的反步法的空战机动控制方法,该方法可以保证飞机在做特定机动过程中,通过设计特定的Lyapunov函数,运用带约束的反步法,将角度态势信息考虑到控制中,得到带有角度态势约束的反步法控制律。最后通过仿真验证了在斤斗机动和上半滚倒转机动中,该方法能考虑到态势变化并有效地使得飞机角度态势朝优势发展。
1 一对一空战问题描述一对一空战过程中,己机通常根据敌机的相对位置、航向等信息,采取相应的机动进行应对。因此空战决策通常可以分为态势评估部分和机动动作设计部分。
1.1 态势模型一对一空战态势模型实质上是敌我两机在对方导弹攻击区的可能性模型。而导弹攻击区是指载机在一定的发射条件下导弹可以命中的空间范围。在态势评估中,通常将这种模型分解成4个方面,分别是速度、高度、距离和角度。
本文主要目标是将态势信息引入到底层控制中,用角度态势对飞机的横滚模态进行修正。
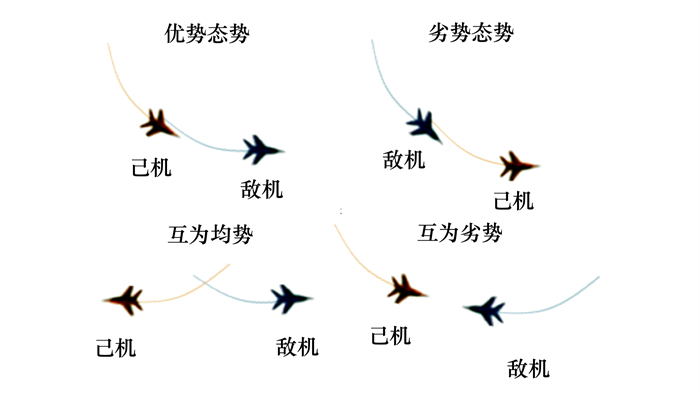
在角度态势上, 可以由目标方位角和目标进入角来确定态势数值。通常用p表示目标方位角, 即攻击机速度矢量与目标线的夹角; 用q表示目标进入角, 即目标机的速度矢量与目标线的夹角。当|p|≤π/2, |q|≤π/2时, 己机处于优势态势; 当|p|>π/2, |q|>π/2时, 己机处于劣势态势; 当|p|>π/2, |q|≤π/2时, 己机处于互为均势态势; 当|p|≤π/2, |q|>π/2时, 己机处于劣势态势。具体态势情况可以参考图 1。
|
| 图 1 空战基本态势 |
在对角度态势建模时, 忽略导弹最大离轴发射角和最大搜索方位角, 认为在目标进入角不变时, 目标方位角为0时态势最优, 为π时态势最劣, 基于这种思想, 对目标方位角进行划分, 可以得到近似的角度态势模型为
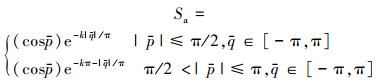
|
(1) |
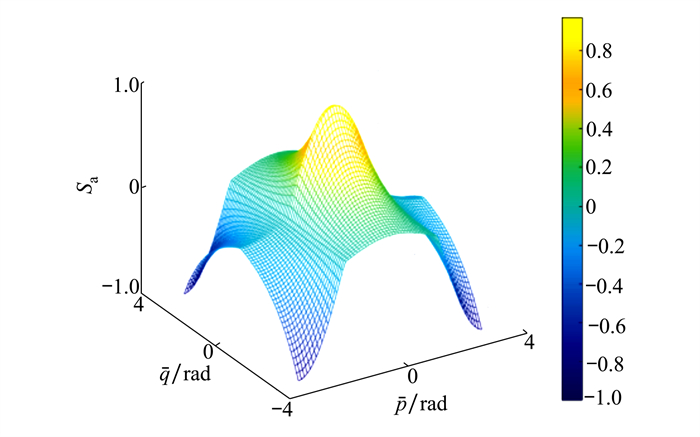
式中, Sa为角度态势值, 范围在[-1, 1], 大于0时表示优势, 小于0时表示劣势。其态势与目标方位角和目标进入角之间的关系如图 2所示。
|
| 图 2 角度态势图 |
由图 2可以看出, 在目标进入角q=0, 目标方位角p=0时, 此时己机机头指向敌机尾部, 为优势态势, 模型中角度态势最好, 数值为1;在目标进入角q=π, 目标方位角p=π时, 敌机机头指向己机尾部, 为劣势态势, 模型中角度态势最差, 数值为-1;在目标进入角q=0, 目标方位角p=π时, 此时敌机和己机属于各自背离情况, 为互为均势态势, 模型中的态势数值约为-0.14, 在0附近, 比较合理; 在目标进入角q=π, 目标方位角p=0时, 敌机和己机属于迎面机头相对的情况, 为互为劣势态势, 模型中的态势数值约为0.14, 在0附近, 比较合理。
1.2 机动动作设计通常机动动作库的设计有2种思路: ①NASA提出的7种基本的机动动作; ②使用典型战术机动的动作库, 比如眼镜蛇机动、斤斗等。本节内容主要针对第二种, 对斤斗机动和上半滚倒转机动进行设计。
斤斗动作能够降低前进速度, 能将劣势态势转为优势, 同时在躲避空空导弹上也起到作用。关于斤斗动作的控制通常是分阶段的, 根据飞机所处的不同状态, 选择合适的控制目标。下面给出斤斗动作的执行流程。
| 状态序号 | 条件 | 控制目标 |
| 1 | 执行机动前 | 定常平飞 |
| 2 | θ∈(0°, 80°) | Nz=4, φ=0 |
| 3 | θ∈(80°, 90°)∪(90°, 80°) | Nz=4, p=0 |
| 4 | θ∈(80°, -80°) | Nz=4, φ=180° |
| 5 | θ∈(-80°, -90°)∪(-90°, -80°) | Nz=4, p=0 |
| 6 | θ∈(-80°, 0°) | Nz=4, φ=0 |
| 7 | 机动完成 | 定常平飞 |
上半滚倒转在前半段同斤斗一样, 使飞机拉起, 后面通过控制滚转角, 将飞机回正。因此, 可以给出上半滚倒转机动流程。
| 状态序号 | 条件 | 控制目标 |
| 1 | 执行机动前 | 定常平飞 |
| 2 | θ∈(0, 80°) | Nz=4, φ=0 |
| 3 | θ∈(80°, 90°)∪(90°, 80°) | Nz=4, p=0 |
| 4 | θ∈(80°, 0°) | Nz=4, φ=180° |
| 5 | θ∈(-10°, 10°) | Nz=0, φ=0 |
| 6 | 机动完成 | 定常平飞 |
飞行过程中, 飞机的状态量存在各类物理条件下的约束, 比如速度迎角和高度应该在飞行包线内, 控制律的舵面输出存在速度和位置的限制等。这些约束在常规飞行下不会影响飞机的稳定, 然而当飞机在机动飞行或者需要给出大的指令信号时, 由控制律输出的数值很容易导致舵面饱和, 进而影响系统的稳定性。
本节将对这类自身约束的飞机进行反步法的飞行控制律设计。
2.1 控制律设计以六自由度飞机模型为例, 给出飞机速度, 气流角和角速度的微分方程
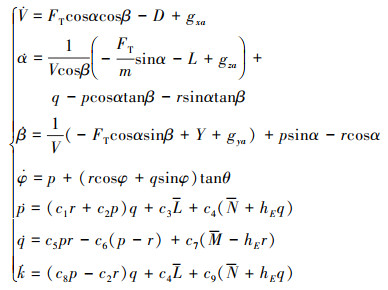
|
(2) |
(2) 式可写成

|
(3) |
其中,角度回路中, 系统状态为气流角和角速率xαβφ= [αβφ]T, xpqr= [pqr] T, 系统输入为升降舵、副翼和方向舵u= [δeδaδr]T, 速度回路中系统状态是V, 系统输入是发动机推力FT, 其中fαβφ(x)为方程中不含角速度的项, gαβφ(x)为角速度状态量的系数矩阵, fpqr(x)为方程中不含舵面产生的力矩的项, gpqr(x)为系统输入的系数矩阵。定义如下

|
(4) |
由模型(2)可以看出气流角和发动机推力都影响着速度变化, 同时发动机推力, 速度和角速度又影响着气流角变化, 速度和气流角存在着耦合作用, 但由模型可以看出, 这种耦合作用因为系数cosαcosβ和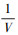
根据模型(3)设计控制律, 首先对速度通道控制律进行设计。
定义速度的跟踪误差zV和修正后的跟踪误差zV如下
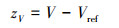
|
(5) |

|
(6) |
式中,χV为误差的修正量。设Lyapunov函数为
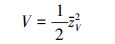
|
(7) |
对(7)式求导

|
(8) |
因为V≥0成立, 因此只需保证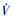
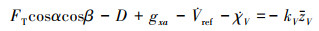
|
(9) |
又需使得zV→0, zV→0成立, 即(10)式需成立

|
(10) |
由(9)式和(10)式可得控制律为
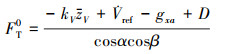
|
(11) |

|
(12) |
式中:FT0为控制律解算出的结果;FT表示由指令滤波器输出后的结果;χV初值为0。其中指令滤波器可以用相应的约束对控制律输出进行限制, 这里对推力的位置和速率进行限制。
然后对气流角回路控制律进行设计, 定义气流角误差变量和修正误差变量
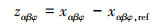
|
(13) |
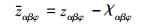
|
(14) |
式中,χαβφ为气流角修正值。可得虚拟控制律为
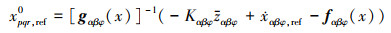
|
(15) |
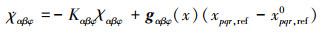
|
(16) |
式中:xpqr, ref0为控制律解算出的结果;xpqr, ref表示由指令滤波器输出后的结果。进一步定义角速度误差变量和修正误差变量
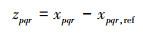
|
(17) |
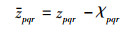
|
(18) |
可得控制律为
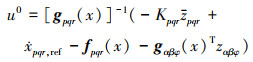
|
(19) |
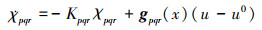
|
(20) |
式中:u0为控制律解算出的结果;u表示由指令滤波器输出后的结果, 指令滤波器结构如图 3所示。

|
| 图 3 控制律输出的指令滤波器结构 |
设Lyapunov函数为
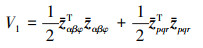
|
(21) |
两边求导
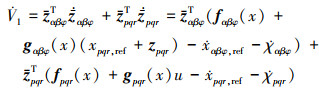
|
(22) |
将(16)式和(20)式带入(22)式可得
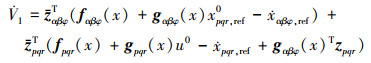
|
(23) |
由(4)式可以看出gαβφ(x), gpqr(x)都是满秩的, 因此二者可以直接求逆, 并且控制律结果是唯一的, 不存在奇异情况。
将虚拟控制律(15)式和控制律(19)式带入(23)式得

|
(24) |
因为V1≥0, 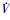

在空战过程中, 飞机在采取特殊机动, 如斤斗、上半滚倒转这类机动时, 能够通过这类机动取得优势, 但同时, 这种特殊机动需要持续约20~60 s不等的时间, 而在这段时间内, 己机的未来运动轨迹很容易被预测, 如果敌机采取针对动作时, 己机需要尽快切出这个机动, 否则会十分被动。
因此飞机在做机动的过程中, 还应该考虑两机之间的态势变化, 如果在做常规的机动控制中包含态势的信息, 将更有利于空战中己机的生存率。
3.1 修正误差更新律设计这里将角度约束增加到控制律中, 对角度态势改变最有效的是控制航迹滚转角, 由前文内容可知约束反步法的控制律输出, 在带有态势约束的情况下, 设修正误差为

|
(25) |
式中:χμ为航迹滚转角的修正量;c为方向参数, 取值为±1。则可得虚拟控制律和修正量χμ的更新律为
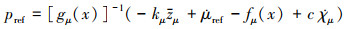
|
(26) |
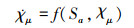
|
(27) |
式中:kμ为正数, 是控制律增益, 同时也表示修正量收敛到0的快慢;f(*)为态势到修正程度的函数, 根据态势的优劣程度, 设置相应的函数使得修正量始终向态势变优的方向发展。因此控制律的重点就在于求解f(*)的表达形式。
在(27)式的作用下, 当态势值为优势时, 此时χμ在f(Sa, χμ)控制下应该朝向0变化。当态势为劣势时, 在f(Sa, χμ)控制下χμ存在一定的偏差来修正原本的控制量。因此可以得到f(Sa, χμ)的大致表达式

|
(28) |
式中,kS为正数, 表示态势对修正量影响的程度。由上表达可知, 当态势为优势时, 修正量会朝向0变化, 当态势为劣势时, 修正量会远离0变化。然后通过c控制误差变量zμ向zμ的变化方向, 其表达为
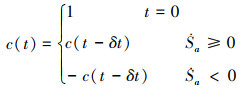
|
(29) |
由(29)式可知, 在初始时刻, c为1, 然后c的取值将由上一拍的c决定。如果态势朝优势变化, 则c不变, 认为此时的修正量对误差的修正方向不变; 如果态势朝劣势变化, 则c取反, 认为此时的修正量对误差的修正方向应该反向。
3.2 障碍Lyapunov函数修正误差更新律是将态势信息转换成航迹滚转角的指令数值, 这一过程中需要考虑修正误差的定义范围。这里引入障碍Lyapunov函数, 障碍Lyapunov函数是一种特殊的Lyapunov函数, 常见形式有分数形式, 对数形式或者正切形式。当状态量在区间边界附近时, 其导数会非常大, 阻止状态量越出边界。
对于原修正误差χμ, 可以定义Lyapunov函数为

|
(30) |
则(30)式的导数为
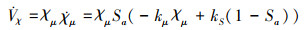
|
(31) |
当态势为优势时, 即Sa>0时, 忽略χμ的更新输入, 有

|
(32) |
现使用障碍Lyapunov函数进行改进
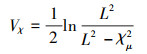
|
(33) |
式中,L为χμ的边界, 即可认为χμ∈(-L, L), 则χμ的更新律可改进为
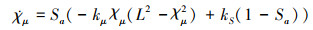
|
(34) |
设Lyapunov函数为

|
(35) |
对其求导得
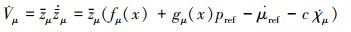
|
(36) |
将(26)式和(34)式带入(36)式可得
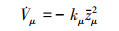
|
(37) |
因此可以证明zμ→0, 又因为zμ=zμ-c·χμ, 所以要想进一步证明zμ→0, 则需证明χμ→0。
当态势为优势时, 即Sa>0时, 设Lyapunov函数为
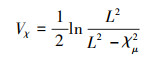
|
(38) |
对(38)式求导, 将(34)式代入, 在不考虑输入时
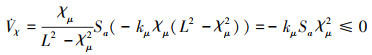
|
(39) |
所以可得χμ→0成立。
当态势不为优势时, 即Sa≤0时, (34)式的特征值大于零, 则χμ发散, 且满足χμ∈(-L, L)。此时zμ在(29)式中c的控制方向下将系统向优势方向变化。
此时系统满足修正误差趋于0, 即zμ→0, 而跟踪误差zμ→χμ。此时修正量起作用。
由稳定性分析可知, 在系统处于优势时, 此时修正量会很快趋于零, 即优势状态下, 基本不会对系统指令进行修正。而在系统处于劣势时, 此时控制律的修正量将起作用, 通过对滚转角虚拟控制律进行修正, 确保系统的态势向优势变化。
4 仿真验证仿真中使用F-16飞机进行空中对抗模拟。首先给出初始状态己机为劣势时, 采用斤斗机动的仿真结果。其中飞机的初始状态包括三轴位置以及速度、航迹倾斜角和航机方位角用[x, y, h, V, γ, χ]表示, 敌机初始状态为[1 500, 4 000, 3 000, 150, 0, 0], 己机初始状态为[0, 0, 3 000, 150, 0, 0]。
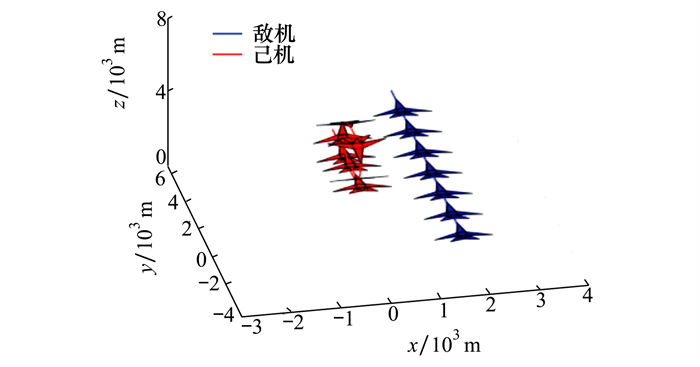
|
| 图 4 直接斤斗机动双机轨迹 |
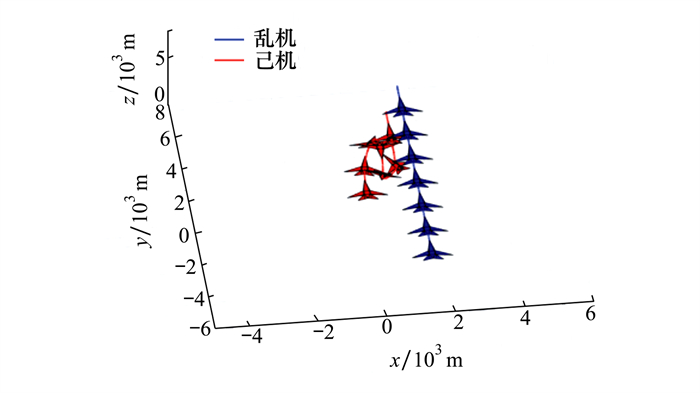
|
| 图 5 带角度态势约束的斤斗机动双机轨迹 |
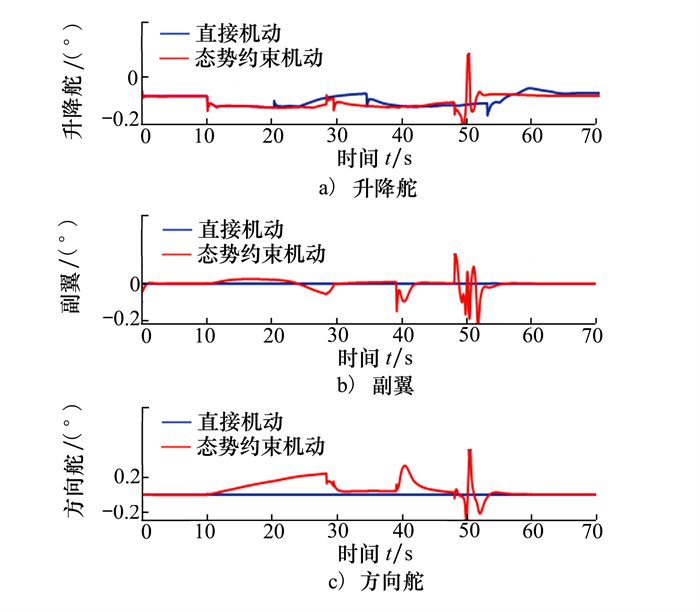
|
| 图 6 上半滚倒转机动2种方法舵面输出对比 |

|
| 图 7 斤斗机动2种方法角度态势对比 |
由仿真结果可以看出,在仿真起始时,己机处于劣势态势,此时在修正误差的作用下,己机向右侧偏,态势逐渐增大。随后在斤斗翻转的过程中,己机最终会从劣势转成优势。带了态势约束的斤斗机动比直接机动在系统态势上有了一定提升。
然后给出己机在初始状态处于互为均势时,采用上半滚倒转的仿真结果。其中飞机的初始状态包括三轴位置以及速度、航迹倾斜角和航机方位角[x, y, h, V, γ, χ],敌机为[1 000, 3 000, 3 000, 150, 0, 0],己机为[0, 0, 3 000, 150, 0, 0]。
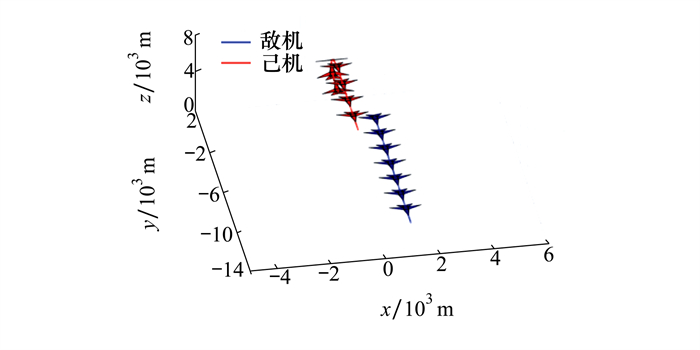
|
| 图 8 直接上半滚倒转机动双机轨迹 |
|
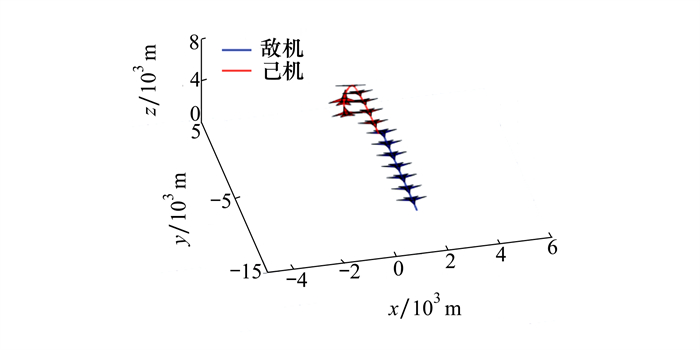
| 图 9 带角度态势约束的上半滚倒转机动双机轨迹 |
由仿真结果可以看出,开始时己机处于互为均势,在修正误差的作用下,己机开始向右侧偏,到飞机俯仰角翻转180°后,己机态势最终变为优势。带了态势约束的上半滚倒转机动比直接机动在系统态势上有了一定提升。
|
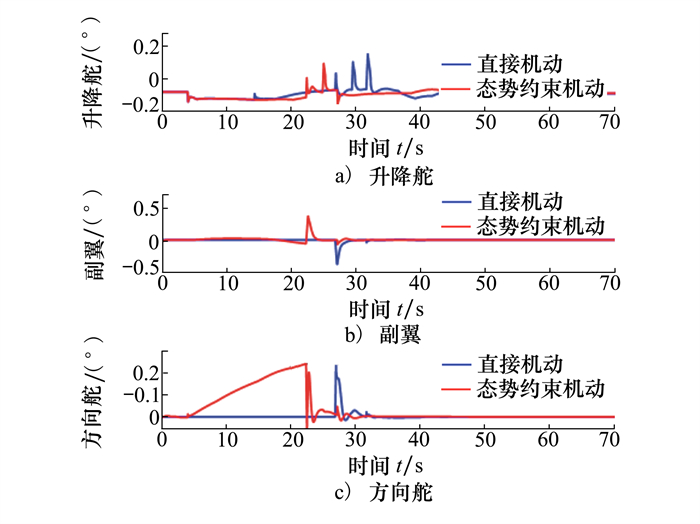
| 图 10 上半滚倒转机动2种方法舵面输出对比 |

|
| 图 11 上半滚倒转机动2种方法态势值对比 |
针对机动飞行过程中,己机会受到敌机机动飞行的影响,导致态势变差的问题,本文提出了一种带有态势约束的机动控制律设计方法。将态势信息作为约束,引入到底层控制律中,当飞机处在劣势态势时,控制律会通过修正误差使飞机态势朝优势变化;而当飞机优势时,则修正误差会很快收敛至零。通过斤斗机动和上半滚倒转机动的仿真验证表明,将态势信息引入控制律设计中,己机的飞行轨迹更优,态势得到了很大提升。本文为飞机空战的控制提供了一种新的思路,这和微分对策等最优求解的方法有所不同。微分对策这类方法则更重视对优化目标函数的求解,以得到最优空战态势,而本文的方法认为态势信息不止作为决策的输入,还可以作为控制器的补偿值,这种方法更加看重系统的稳定性,其次是提升空战态势。最后,本文只是引入了态势估计的一部分,即角度态势,并补偿到横滚通道控制量中,而对于更全面的态势,以及对应的控制分配问题还需要进一步的研究。
| [1] | JARMARK B. A missile duel between two aircraft[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(4): 508-513. DOI:10.2514/3.20012 |
| [2] | JARMARK B. A realistic aerial combat duel as a differential game study[C]//IEEE Conference on Decision & Control, 1983 |
| [3] | IMADO F, MIWA S. The optimal evasive maneuver of a fighter against proportional navigation missiles[C]//10th Atmospheric Flight Mechanics Conference, 1983 |
| [4] | BYRNES M W. Nightfall: machine autonomy in air-to-air combat[J]. Air and Space Power Journal, 2014, 28(3): 48-75. |
| [5] |
李清伟, 刘超, 贺嘉璠. 空战分层决策模型构建方法[C]//第八届中国指挥控制大会, 2020 LI Qingwei, LIU Chao, HE Jiafan. The constructing method of hierarchical decision-making model in air combat[C]//Proceedings of the 8th China Command and Control Conference, 2020(in Chinese) |
| [6] |
徐安, 陈星, 李战武, 等. 基于战术攻击区的超视距空战态势评估方法[J]. 火力与指挥控制, 2020, 45(9): 97-102.
XU An, CHEN Xing, LI Zhanwu, et al. A method of situation assessment for beyond-visual-range aircombat based on tactical attack area[J]. Fire Control & Command Control, 2020, 45(9): 97-102. (in Chinese) DOI:10.3969/j.issn.1002-0640.2020.09.018 |
| [7] |
史振庆, 梁晓龙, 张佳强, 等. 基于导弹攻击区的空战态势评估[J]. 火力与指挥控制, 2018, 43(9): 89-93.
SHI Zhenqing, LIANG Xiaolong, ZHANG Jiaqiang, et al. Situation assessment for air combat based on missile attack zone[J]. Fire Control & Command Control, 2018, 43(9): 89-93. (in Chinese) DOI:10.3969/j.issn.1002-0640.2018.09.019 |
| [8] |
兰轶冰, 王维嘉, 宋科璞. 基于导弹攻击区的空战战术决策方法研究[J]. 电光与控制, 2020, 27(10): 8-11.
LAN Yibing, WANG Weijia, SONG Kepu. Air combat tactical decision-making based on missile attack envelop[J]. Electronics Optics & Control, 2020, 27(10): 8-11. (in Chinese) DOI:10.3969/j.issn.1671-637X.2020.10.002 |
| [9] |
王光辉, 徐光达, 谢宇鹏, 等. 区间数模糊综合评判的UCAV空战威胁评估[J]. 现代防御技术, 2018, 46(6): 1-6.
WANG Guanghui, XU Guangda, XIE Yupeng, et al. UCAV air combat threat assessment based on interval number fuzzy comprehensive evaluation[J]. Modern Defence Technology, 2018, 46(6): 1-6. (in Chinese) |
| [10] |
赵克新, 黄长强, 魏政磊, 等. 改进决策树的无人机空战态势估计[J]. 哈尔滨工业大学学报, 2019, 51(4): 72-79.
ZHAO Kexin, HUANG Changqiang, WEI Zhenglei, et al. Situation assessment for unmanned aerial vehicle air combat based on anti-reasoning rules decision tree[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 72-79. (in Chinese) |
| [11] | XUAN Y B, HUANG C Q, LI W X. Air combat situation assessment by gray fuzzy Bayesian network[J]. Applied Mechanics & Materials, 2011, 69: 114-119. |
| [12] |
姜龙亭, 寇雅楠, 王栋, 等. 动态变权重的近距空战态势评估方法[J]. 电光与控制, 2019, 26(4): 1-5.
JIANG Longting, KOU Yanan, WANG Dong, et al. A dynamic variable weight method for situation assessment in close-range air combat[J]. Electronics Optics & Control, 2019, 26(4): 1-5. (in Chinese) |
| [13] |
谢建峰, 杨啟明, 戴树岭, 等. 基于强化遗传算法的无人机空战机动决策研究[J]. 西北工业大学学报, 2020, 38(6): 1330-1338.
XIE Jianfeng, YANG Qiming, DAI Shuling, et al. Air combat maneuver decision based on reinforcement genetic algorithm[J]. Journal of Northwestern Polytechnical University, 2020, 38(6): 1330-1338. (in Chinese) DOI:10.3969/j.issn.1000-2758.2020.06.024 |
| [14] |
谢俊洁. 空战仿真中的目标分配与火力分配方法[D]. 长沙: 国防科技大学, 2016 XIE Junjie. Target allocation and firepower allocation in air combat simulation[D]. Changsha: University of Defense Science and Technology, 2016(in Chinese) |
| [15] | LOWE R, WU Y, TAMAR A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[C]//Advances in Neural Information Processing Systems, 2017 |
| [16] |
蓝伟华. 对抗空战仿真数学建模[J]. 电光与控制, 2009(6): 9-11.
LAN Weihua. Mathematical modeling of air combat simulation[J]. Electronics Optics & Control, 2009(6): 9-11. (in Chinese) DOI:10.3969/j.issn.1671-637X.2009.06.003 |
| [17] |
刘佩, 王维嘉, 陈向, 等. 空战机动飞行轨迹生成与控制[J]. 兵工自动化, 2018, 37(11): 76-80.
LIU Pei, WANG Weijia, CHEN Xiang, et al. Air combat maneuvering flight trajectory generation and control[J]. Ordnance Industry Automation, 2018, 37(11): 76-80. (in Chinese) |
2. Shaanxi Province Key Laboratory of Flight Control and Simulation Technology, Xi'an 710129, China




