2. 中航工业雷华电子技术研究所, 江苏 无锡 214063;
3. 西北工业大学 数学与统计学院, 陕西 西安 710072
脉冲压缩体制雷达的发射波形设计和接收滤波器优化是雷达信号处理领域中的热点问题[1-3]。在复杂电磁环境中,杂波和噪声分量会对雷达目标探测造成旁瓣升高等不良影响。众所周知,匹配滤波器(matched filter, MF)是假设接收信号中只包含高斯白噪声和单点反射信号时,基于最大信噪比准则所推导得出的最优滤波器。以线性调频信号为例,在其匹配滤波器的脉压输出中,主瓣的临近区域会出现较高的距离旁瓣,造成微弱目标淹没。因此,有必要设计非匹配滤波器以抑制距离旁瓣来改善探测效果。
非匹配滤波器设计的研究大致分为如下2种:
1) 在固定雷达发射波形情况下的非匹配滤波器设计。常见的雷达发射波形有线性调频波形、相位编码波形等。在雷达发射机端配置固定的情况下,非匹配滤波器设计可以形成优于匹配滤波器的旁瓣抑制效果。例如,Cilliers和Smit[4]基于p-范数设计非匹配滤波器,最小化积分旁瓣水平(integrated sidelobe level, ISL)或者峰值旁瓣水平(peak sidelobe level, PSL),并探究非匹配滤波器的长度和p-范数类型对探测效果的影响。De Maio和Rabaste等[5-6]使用二次约束二次规划(quadratically constrained quadratic programming, QCQP)等凸优化方法进行非匹配滤波器设计,研究滤波器长度等因素对旁瓣抑制效果的影响。
2) 雷达发射波形和非匹配滤波器联合设计。Stoica等[7]提出了多个迭代优化算法,通过构造与ISL相关的加权矩阵,设计出具有良好自相关特性的恒模波形;Jiu等[8]结合当前电磁环境中的干扰源先验信息,通过开展发射波形和非匹配滤波器的联合设计,实现信干噪比的极大提升;Zhou等[9]通过开展波形和滤波器的联合设计,实现对间歇采样转发干扰的有效抑制。
现有方法[4-9]设计出的与波形长度相同的非匹配滤波器得到的旁瓣层未达到满意的效果。为获得良好的旁瓣抑制效果,往往采用超过信号长度2倍以上甚至更长的非匹配滤波器序列。为改善上述情况,本文研究恒模波形和非匹配滤波器联合设计问题。在设计过程中,非匹配滤波器长度与波形长度相同,以最小化旁瓣层作为优化问题的目标函数,结合交替方向乘子法求解最优非匹配滤波器,将目标函数拆成多个子问题分开求解。此外,本文还将上述方法扩展用于给定波形时的非匹配滤波器设计问题。在实际应用中可以根据硬件平台的自由度情况灵活选择模型。
1 非匹配滤波器优化模型构造 1.1 恒模波形和非匹配滤波器联合设计令x=[x1, …, xM]T表示包含M个码元的雷达发射信号, w=[w1, …, wM]T表示与之长度相同的非匹配滤波器序列。暂不考虑噪声作用, 采用非匹配滤波器脉压后, 长度为2M-1的输出结果可表示为
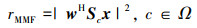
|
(1) |
式中: M×M的选择矩阵Sc的u行v列的元素满足Sc(u, v) 
设主瓣宽度为2N+1, [M-N, M+N]表示非匹配滤波器输出的主瓣区域序号。把主瓣区域从Ω中去除即可得到旁瓣区域序号集合Υ。为最大限度地抑制旁瓣, 本文考虑以最小化旁瓣峰值与主瓣峰值之比为目的, 建立如下极小极大化优化模型
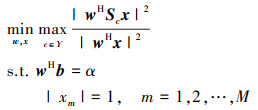
|
(2) |
式中, b=[1, 01×M-1]T, 引入其可以保证解出的w首元素为α, 便于在实际过程中实现对w的幅度调控。
1.2 针对固定发射波形的非匹配滤波器设计当波形x给定的情况下, 上述模型退化为非匹配滤波器设计问题
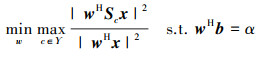
|
(3) |
通过前述建模过程可以看出, 公式(3)是公式(2)的简化拓展, 因此在本节将着重阐述公式(2)的求解。假设w′和x′为公式(2)的最优解, 再令μ′=|(w′)H x′|2, 于是有下列归一化过程
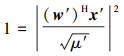
|
(4) |
在公式(3)的表达中引入辅助变量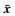
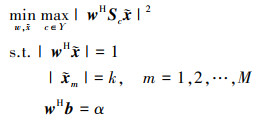
|
(5) |
为实现恒模约束与目标函数解耦, 设置
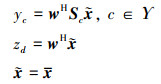
|
(6) |
于是公式(5)被重新表示为
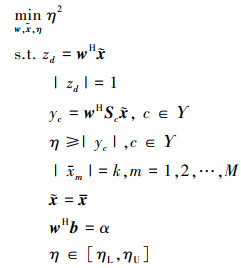
|
(7) |
下面根据公式(7)构建出拉格朗日增广函数
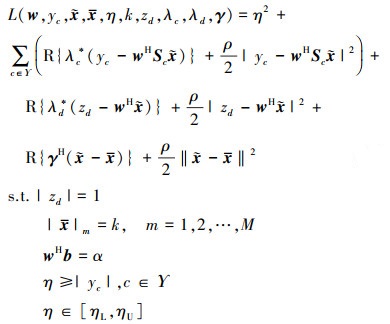
|
(8) |
式中:R{*}表示取*的实部;λc, λd, γ分别是约束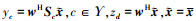
基于ADMM算法框架[10], 给出求解公式(8)的迭代算法步骤(其中t代表迭代次数):
1) 使用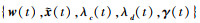
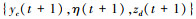
(1) 使用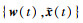
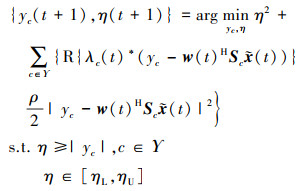
|
(9) |
然后定义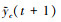
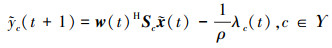
|
(10) |
于是公式(9)就转化为
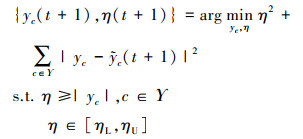
|
(11) |
然后可以得出
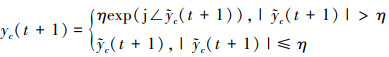
|
(12) |
式中:j表示虚数单位;∠表示取[*]的相位。下面定义以η, yc(t+1)为变量的阶跃函数[10]
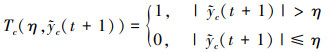
|
(13) |
结合阶跃函数的性质, 公式(11)就转换为关于η的单变量问题

|
(14) |
从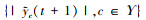
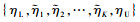
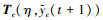
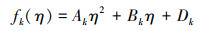
|
(15) |
式中, Ak, Bk, Dk的取值分别为
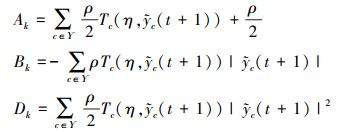
|
(16) |
对于第k个子区间, 将存在以下3种情况:
情况1: 当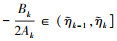
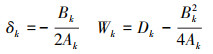
|
(17) |
情况2: 当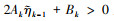
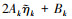
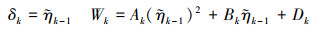
|
(18) |
情况3: 当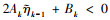
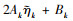

|
(19) |
通过对各个子区间进行遍历, 可以得到K+1个Wk, 设置We=min{Wk, k=1, …, K+1}, e为最小值对应的索引, 于是
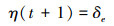
|
(20) |
(2) 使用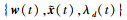
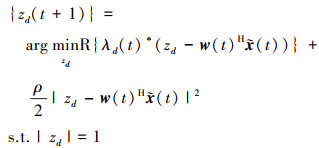
|
(21) |
然后定义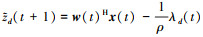
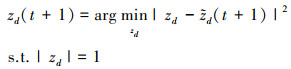
|
(22) |
于是有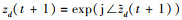
2) 用{yc(t+1), zd(t+1), x(t), λc(t), λd(t), γ(t)}求解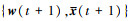
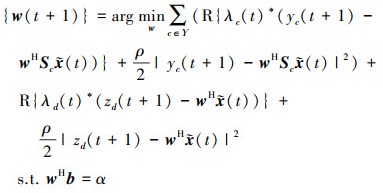
|
(23) |
将上述表达式简化为
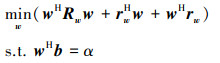
|
(24) |
式中
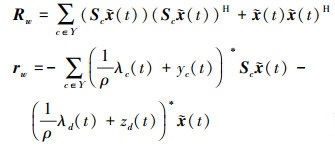
|
(25) |
结合约束条件构建拉格朗日增广函数
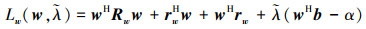
|
(26) |
通过对w求偏导数并令其为0可以得到
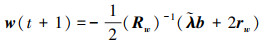
|
(27) |
将其带入到(24)式中的线性约束可以得出
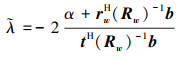
|
(28) |
将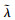
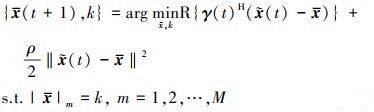
|
(29) |
易见公式(29)等价于下列形式
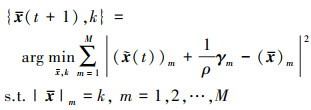
|
(30) |
公式(30)满足最优性条件时, x和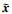
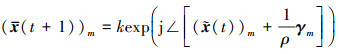
|
(31) |
于是(30)式就变成关于k的单变量问题
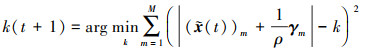
|
(32) |
可以解出
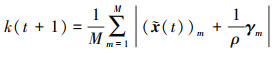
|
(33) |
将(33)式代入(31)式即可得到x(t+1)。
3) 使用{ w(t+1)yc(t+1), zd(t+1), x(t+1)}以及{λc(t), λd(t), γ(t)}求解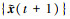
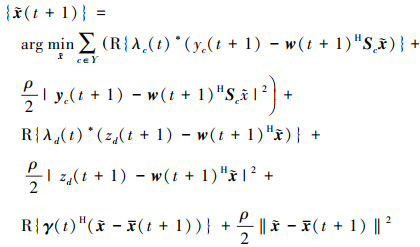
|
(34) |
将公式(34)简化成
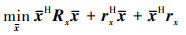
|
(35) |
式中

|
(36) |
结合(24)~(27)式的求解过程, 可以得到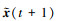
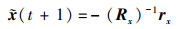
|
(37) |
4) 更新拉格朗日乘子
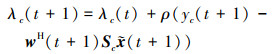
|
(38) |
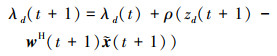
|
(39) |
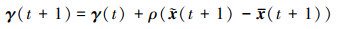
|
(40) |
根据上述4步进行迭代得到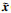
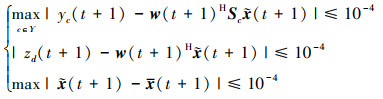
|
(41) |
针对计算复杂度的分析, 侧重每次迭代过程中比较耗费资源的乘法运算和矩阵求逆。假定序号集合Υ中元素个数为F, 总迭代次数为T0, 则总计算复杂度为: Ο(F2T0+2N3T0+(F+2)MT0); 文献[7]中对比算法的计算复杂度为Ο(NT0lg(N)); 文献[13]中对比算法的计算复杂度为Ο(10NT0)。
3 仿真及分析 3.1 针对线性调频信号的非匹配滤波器设计线性调频信号(linear frequency modulation, LFM)具有良好的脉压性能和便捷的调制方式, 其在雷达系统中得到广泛的应用。带宽B=10 MHz、时宽Tp=5 μs的LFM信号, 采样频率fs=2.5B。同时设置N=3, ρ=2, α=1, [ηL, ηU]=[10-7, 1], 最大迭代次数T=20 000。
在本实验中(实验1), 将采用4种方法: 匹配滤波器、加Hamming窗、QCQP方法产生的非匹配滤波器[11]、本文方法(方法1)得到峰值旁瓣输出情况、3 dB主瓣宽度进行对比。定义归一化峰值旁瓣水平
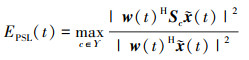
|
(42) |
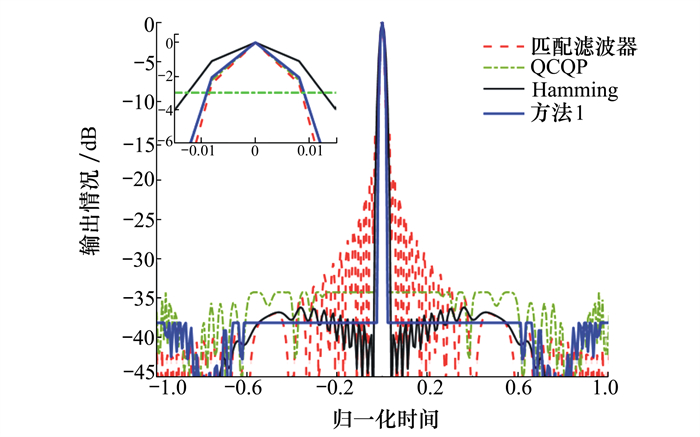
通过图 1的实验结果可以看出, 在设定的旁瓣区域上, 匹配滤波器、QCQP[11]、Hamming窗以及本文方法的峰值旁瓣表现分别为-14.13, -34.27, -36.18, -38.16 dB; 结合反映3 dB主瓣宽度的子图表明, QCQP方法[11]和本方法可以实现与匹配滤波器相同的主瓣宽度, 而本方法获得的旁瓣更低。
|
| 图 1 4种方法输出情况对比(实验1) |
通过图 2迭代情况可以看出, 本方法在1 000次迭代后就实现收敛, 这说明本文方法具备较好的收敛性。

|
| 图 2 归一化旁瓣随迭代次数变化趋势(实验1) |
根据前述采样频率计算出距离门ds=c/2fs, c为光速。以文献[12]中扩展目标SR-71侦察机的散射特征为例, 设置5个主散射点,距离分布和信噪比设置如表 1所示(噪声为高斯白噪声)。
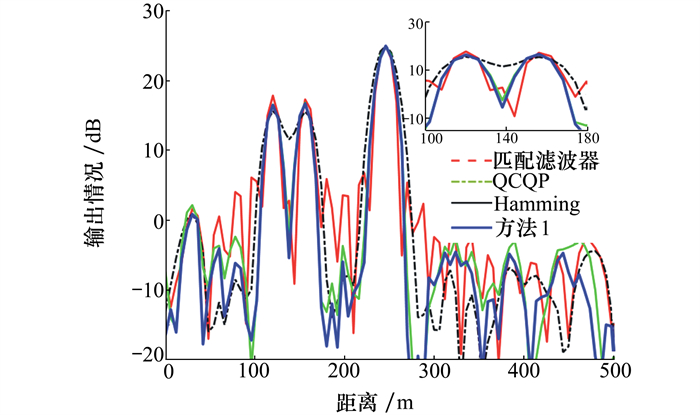
图 3结果表明: ①匹配滤波器方法在散射点1和2的周围出现很高的旁瓣, 极易出现虚警; ②加Hamming窗的方法虽然可以有效抑制旁瓣, 但分辨率下降造成无法有效区分散射点1和2;③QCQP[11]方法虽实现旁瓣抑制和较高分辨率, 但本文方法可以与之相比具有更低的旁瓣水平和同等的分辨率。④对于间距过近的散射点3和4, 4种方法都无法分辨。
|
| 图 3 目标特征提取情况(实验1) |
在本小节中(实验2), 匹配滤波器方法和LFM信号仍将会被纳入到对比范围中, 在此控制待设计波形与LFM具有相同的带宽。新LFM信号的带宽B=50 MHz、时宽Tp=2 μs, 采样频率fs=2B。本文设计出来的相位编码信号, 其带宽为时宽的倒数, 码元数M=100, 其余参数设置为N=0, ρ=2, α=0.001 6, [ηL, ηU]=[10-6, 10-2]。
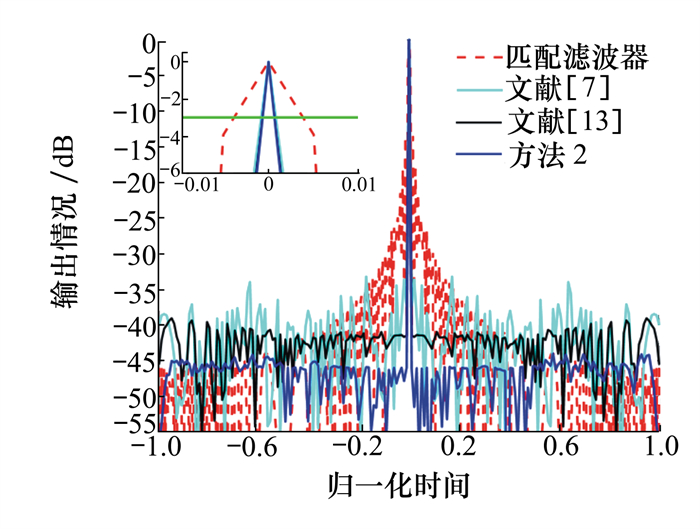
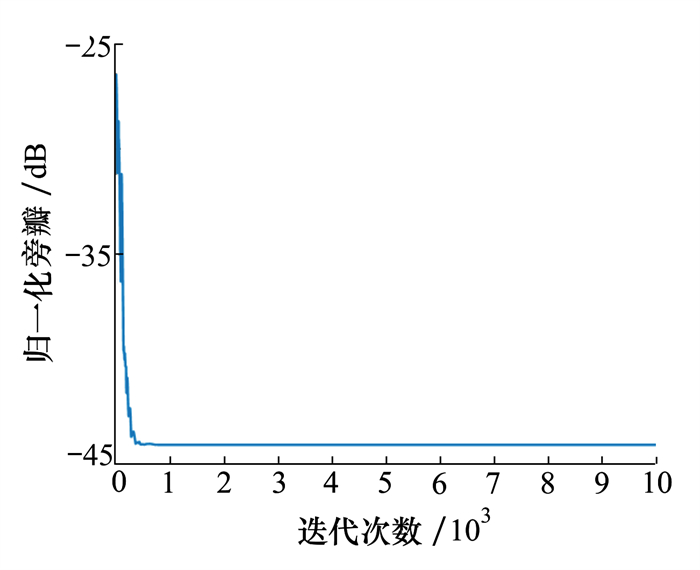
通过图 4的结果可以看出, 匹配滤波器、文献[7]方法、文献[13]方法及本文联合设计方法(方法2)在设定旁瓣区域内的峰值旁瓣分别为-13.49, -33.2, -39.09, -44.01 dB; 同时说明, 通过结合发射端自由度开展恒模波形设计, 3 dB主瓣宽度将会得到显著减小。从图 5迭代情况可以看出, 在约1 000次迭代后, 本方法基本达到收敛。图 7表明, 设计出来的波形吻合恒模约束。
|
| 图 4 4种方法输出情况对比(实验2) |
|
| 图 5 归一化旁瓣随迭代次数变化趋势(实验2) |
|
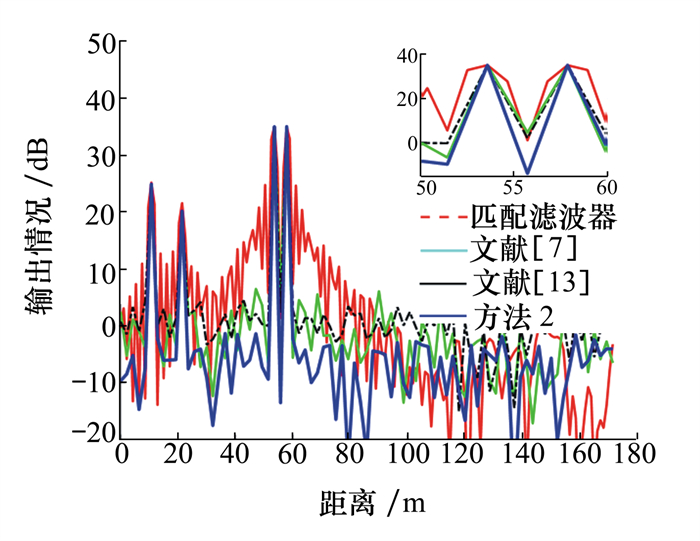
| 图 6 目标特征提取情况(实验2) |

|
| 图 7 波形幅度(实验2) |
沿用表 1散射点参数, 通过图 6的仿真结果可以看出: ①匹配滤波器仍然表现出较高的旁瓣, 散射点周围的旁瓣会形成虚警; ②本方法的目标特征提取效果不仅具有超越实验1的分辨率, 还具有低于文献[7]及文献[13]方法的旁瓣。
4 结论根据雷达发射端可利用自由度情况,本文提出2种优化模型,其以设定旁瓣区域内峰值旁瓣水平最小化为目的实现旁瓣抑制。针对固定体制的发射端,本文设计出与发射波形等长的非匹配滤波器;针对可进行波形优化的发射端,本文提出恒模波形和非匹配滤波器的联合设计。仿真实验结果表明,本次提出的2种算法不仅具有良好的收敛性,而且在目标探测上具有良好的分辨率和干扰抑制效果。
| [1] | ACKROYD M, GHANI F. Optimum mismatched filters for sidelobe suppression[J]. IEEE Trans on Aerospace and Electronic Systems, 1973(2): 214-218. |
| [2] | ZORASTER S. Minimum peak range sidelobe filters for binary phase-coded waveforms[J]. IEEE Trans on Aerospace and Electronic Systems, 1980(1): 112-115. |
| [3] | STOICA P, HE H, LI J. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Trans on Signal Processing, 2012, 60(4): 1730-1740. DOI:10.1109/TSP.2011.2179652 |
| [4] | CILLIERS J E, SMIT J C. Pulse Compression sidelobe reduction by minimization of Lp-Norms[J]. IEEE Trans on Aerospace and Electronic Systems, 2007, 43(3): 1238-1247. DOI:10.1109/TAES.2007.4383616 |
| [5] | DE MAIO A, HUANG Y, PIEZZO M, et al. Design of radar receive filters optimized according to Lp-Norms based criteria[J]. IEEE Trans on Signal Processing, 2011, 59(8): 4023-4029. DOI:10.1109/TSP.2011.2153199 |
| [6] | RABASTE O, SAVY L. Mismatched filter optimization via quadratic convex programming for radar applications[C]//2014 International Radar Conference, Lille, France, 2014 |
| [7] | STOICA P, HE Hao, LI Jian. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Trans on Signal Processing, 2009, 57(4): 1415-1425. DOI:10.1109/TSP.2009.2012562 |
| [8] | JIU B, LIU H, FENG D, et al. Minimax robust transmission waveform and receiving filter design for extended target detection with imprecise prior knowledge[J]. Signal Processing, 2012, 92(1): 210-218. DOI:10.1016/j.sigpro.2011.07.008 |
| [9] | ZHOU K, LI D, SU Y, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610-1614. DOI:10.1109/LSP.2020.3021667 |
| [10] | LIANG J, SO H C, LI J, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Trans on Signal Processing, 2016, 64(20): 5367-5381. DOI:10.1109/TSP.2016.2597123 |
| [11] | RABASTE O, SAVY L. Mismatched filter optimization for radar applications using quadratically constrained quadratic programs[J]. IEEE Trans on Aerospace and Electronic Systems, 2015, 51(4): 3107-3122. DOI:10.1109/TAES.2015.130769 |
| [12] |
陈茜茜, 邓晓波, 张广磊, 等. 峰均功率比约束下扩展目标波形优化[J]. 现代雷达, 2016, 38(9): 32-36.
CHEN Xixi, DENG Xiaobo, ZHANG Guanglei, et al. Waveform design for extended target detection under a peak to average power ratio constraint[J]. Modern Radar, 2016, 38(9): 32-36. (in Chinese) |
| [13] | TAN U, RABASTE O, ADNET C, et al. A sequence-filter joint optimization[C]//26th European Signal Processing Conference, 2018 |
2. AVIC Leihua Electronic Technology Institute, Wuxi 214063, China;
3. School of Mathematics and Statistics, Northwestern Polytechnical University, Xi'an 710072, China




