2. 西北工业大学 无人水下运载技术重点实验室, 陕西 西安 710072
进入21世纪, 海洋已日益成为国际间政治、经济、外交的重要舞台。随着人类海洋活动的频繁, 水下噪声问题日益严重对海洋环境和海洋生物产生了危害,噪声问题也是限制潜艇等水下武器发展的重要因素。因此当前对于水下噪声的降低需求十分迫切。
近年来, 基于仿生流动控制的降噪概念广受科学家及工程师的关注, 为降低噪声提供了新的研究思路。翼型仿生前缘降噪的概念最早来自人类对猫头鹰翅膀结构的认识, 但尖锐锯齿形状的猫头鹰翅膀前缘结构, 其工程实现和应用都具有一定难度和局限。因此针对翼型前缘降噪, 人们逐渐将研究工作重点瞄准对座头鲸鳍肢的前缘凸起结构的模仿。
1995年, Fish等[1]首次发表了座头鲸鳍肢前缘凸起结构的形态学分析和流体力学性能研究。此后许多学者对此结构的流体动力性能进行了研究。Johari等[2]通过水洞试验研究发现波状前缘的添加能够明显改善翼型的失速性能。Wei等[3]通过水洞试验发现低雷诺数下波状前缘能够有效改善翼型的流动分离特性。Pena等[4]通过数值仿真研究了波状前缘翼型对高雷诺数全湍流条件下的翼型水动力性能的影响, 发现相对于过渡条件, 全湍流条件下波状前缘对翼型水动力性能的改善更显著。
Hansen等[5]首次研究了波浪状前缘对翼型单音噪声的控制效果。Chong等[6]通过风洞试验研究了不同波长和振幅对波状前缘降噪效果的影响, 发现增大振幅减小波长可以提高波状前缘的降噪效果。吉林大学的石磊等[7]通过数值模拟研究发现NACA0018翼型前缘添加圆齿状结构后噪声得到降低。Gruber等[8]试验发现, 在串列翼型上同时应用波浪前缘与锯齿尾缘, 可降低翼型噪声5~8.5 dB。英国南安普顿大学声学与振动研究所对波状前缘降噪开展了大量研究[9-11], Clair等[9]通过风洞试验和数值模拟的方法研究发现波状前缘在几乎不影响翼型气动性能的前提下能够降低湍流翼型干涉噪声3~4 dB。Paruchuri等[10]还提出了双周期的新型波状前缘结构。西北工业大学的陈伟杰等[12-13]对波状前缘翼型的气动性能和气动噪声进行了数值及试验研究。哈尔滨工程大学的姜慧[14]研究发现凹凸结构和锯齿叶稍能在一定程度上改善螺旋桨的噪声性能。
目前, 国内外主要还是利用数值方法来模拟研究流噪声, 而CFD和声类比相结合的方法是当前较流行的噪声预测方法。Wang等[15]对噪声计算的混合方法进行了总结介绍。Casalino等[16]采用非定常RANS模型结合FW-H方程来进行噪声数值模拟, 并采用二维网格来减少所需的计算量。Giret等[17]采用LES结合FW-H方程的方法研究了展向尺寸对圆柱翼型干涉噪声的影响。Chen等[18]采用混合LES/FW-H声类比方法研究了波状前缘对圆柱-翼型干涉噪声的影响。
由于水下噪声研究起步较晚, 关于波状前缘对翼型噪声的研究主要集中在气动领域, 对于水下的研究较为匮乏, 而水和空气2种介质在黏性、密度和压缩性上存在很大区别, 使得物体在空气中的流体动力特性和空气动力噪声不能完全模拟其在水中的流体动力特征和水动力噪声[19], 因此关于波状前缘对水下翼型的降噪效果研究是十分必要的。
由于水下环境和水下结构复杂, 水翼可能处于湍流干涉环境中, 如潜艇附体, 泵喷的定子与转子等均处在湍流干涉流场中, 所以研究复杂的干涉环境下波状前缘翼型的降噪效果及降噪机理有很重要的实际应用意义。本文采用湍流翼型干涉噪声的经典模型圆柱-水翼结构, 通过水翼前方圆柱的放置使得水翼处于非定常来流涡街之中, 研究波状前缘对水翼湍流干涉噪声的降噪效果和机理。
1 数值计算方法本文采用流场/声场混合计算方法进行流噪声计算, 其中流场采用大涡模拟(LES)进行计算, 声场采用基于声类比的FW-H方程进行计算。
1.1 大涡模拟对流场的模拟方法主要有直接数值模拟(DNS)、雷诺平均(RANS)、大涡模拟(LES)以及分离涡模拟混合方法(DES)等。LES方法是根据湍流中大尺度涡和小尺度涡的不同特性, 对大尺度的涡直接求解, 对小尺度的涡构建模型来近似。采用滤波函数对非定常不可压缩连续方程和Navier-Stokes方程进行处理, 由此得到
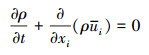
|
(1) |
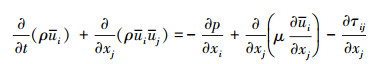
|
(2) |
式中: ρ为流体密度; ui, uj分别是xi, xj方向上的流体分速度; μ为动力黏性系数; p为压强; τij为亚网格尺度应力,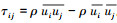
从质量守恒方程和Navier-Stokes方程导出的声波方程为FW-H方程, 可以表示为
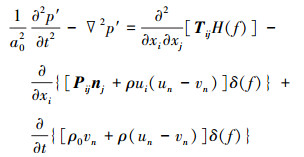
|
(3) |
式中:p′为远场声压, 计算方式为p′=p-p0; ui为xi方向上的流体速度分量; un是垂直于f=0的流体速度分量; vn是垂直于表面的表面速度分量; δ(f)是Dirac delta函数; H(f)为Heaviside函数; 表面f=0为计算模型表面; nj为表面指向外部区域的单位法向量; a0为远场声速; Tij为Lighthill应力张量, 定义为Tij=ρuiuj+Pij-a02(ρ-ρ0)δij。
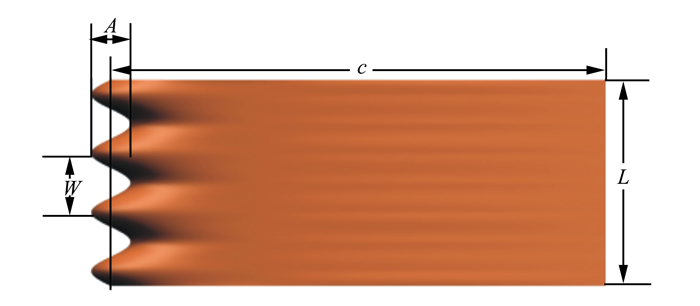
2 模型与边界条件 2.1 物理模型与计算域波状前缘结构见图 1, 以NACA0020为基础翼型, 改型前后的翼型有相同的平均弦长c(100 mm)和展长L(42 mm)。
|
| 图 1 波状前缘翼型示意图 |
波状前缘由2个参数进行定义, 振幅A和波长W。根据座头鲸的生物学测量, 其结节结构的振幅和波长大小分别为2.5%~12%弦长和10%~50%弦长[1], 因此本文选择A=8 mm, W=12 mm的波状前缘翼型作为研究对象, 并在后续研究中简称为A8W12。其弦长沿展向变化定义如公式(4)所示
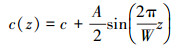
|
(4) |
波状前缘翼型的厚度随中弧线的变化规律如(5)式所示
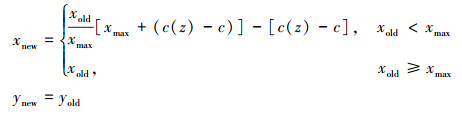
|
(5) |
式中: 下标old表示基础翼型; new表示波状前缘翼型; xmax表示翼型最大厚度的位置。
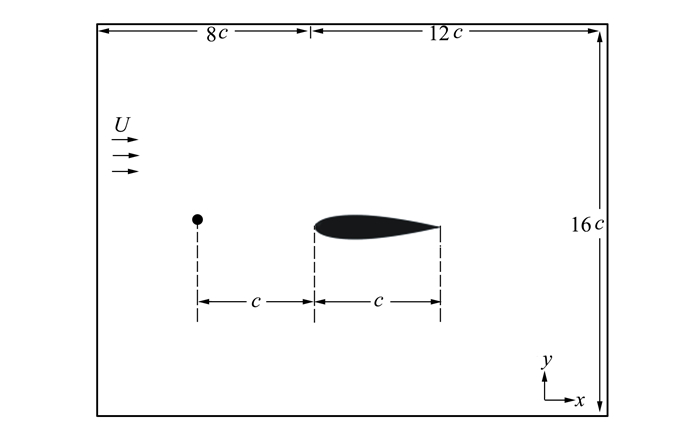
圆柱-翼型湍流干涉模型的计算域设置如图 2所示, 其中圆柱的直径为d=0.1c, 展长与翼型相同, 位于翼型上游一倍弦长处。计算域入口位于翼型前缘上游8倍弦长处, 出口位于翼型前缘下游12倍弦长处, y方向长度为16倍弦长。
|
| 图 2 圆柱-翼型干涉结构示意图 |
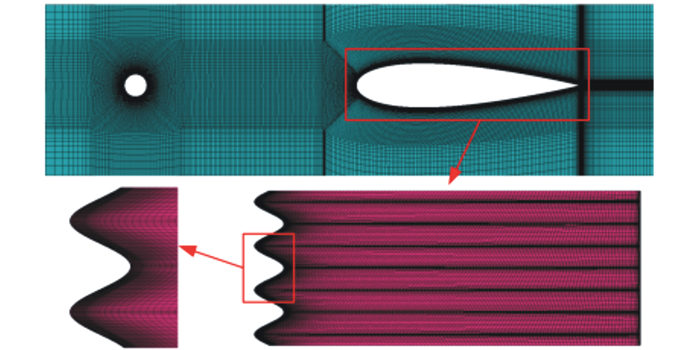
圆柱-翼型湍流干涉模型的局部网格示意图如图 3所示。全域采用结构化网格, 为满足大涡模拟计算的网格要求, 第一层网格与壁面的距离满足y+ < 1, 沿壁面法向网格增长率为1.1。波状前缘翼型网格与基础翼型在x-y平面上基本一致, 但波状结构几何较为复杂, 为精确模拟波状翼型的流场特征, 对其在展向进行了网格加密。
|
| 图 3 圆柱-翼型干涉模型网格示意图 |
计算边界条件设置为: 入口设置为速度入口, U=3.05 m/s, 基于来流速度和翼型弦长的雷诺数为Re=3.05×105, 出口为压力出口, 上下边界为滑移边界条件, 展向设置为周期性边界条件。
计算中亚格子模型选择动力Smagorinsky-Lilly模型, 压力速度耦合方式采用SIMPLEC模型, 动量方程采用有界中心差分格式。首先采用k-ω SST湍流模型进行定常计算, 以定常计算结果作为初场进行LES计算, 计算若干步获得稳定的流场后开启FW-H声学方程采集声学信息, 本文的时间步长为Δt=2.5×10-5。
3 网格与计算方法验证 3.1 网格无关性验证网格密度对计算结果有重要影响, 必须通过网格无关性分析来确定网格密度及质量。本文针对NACA0020和波状前缘翼型干涉模型分别设计了3种网格密度进行网格无关性验证, 以阻力系数平均值和升力系数的均方根值作为参数进行比较, 结果如表 1至2所示。
| 网格号 | 网格数 | 平均阻力系数 | 升力系数均方根 |
| 1 | 5 209 799 | 0.001 3 | 0.081 8 |
| 2 | 7 442 570 | 0.001 5 | 0.084 2 |
| 3 | 10 427 725 | 0.001 6 | 0.083 9 |
| 网格号 | 网格数 | 平均阻力系数 | 升力系数均方根 |
| 1 | 8 513 397 | 0.001 4 | 0.071 6 |
| 2 | 13 309 627 | 0.001 1 | 0.071 8 |
| 3 | 17 862 053 | 0.001 1 | 0.072 4 |
通过表 1和表 2的对比, 发现NACA0020和波状前缘翼型均可选择中等密度网格2, 在保证计算精度的同时提高计算效率。
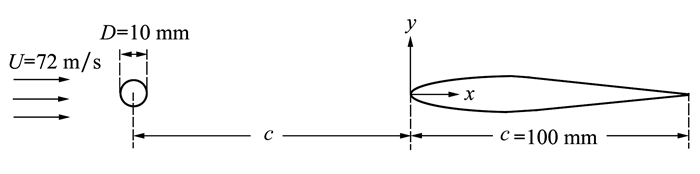
3.2 数值方法验证为确保CFD与声类比方法结合预报流噪声的准确性, 选择与本文模型相似的经典模型圆柱-NACA0012进行验证, 以Jacob等[20]的圆柱翼型干涉噪声风洞试验为参考, 将计算结果与其试验结果进行对比。模型设置见图 4, NACA0012翼型弦长c=100 mm位于圆柱下游1倍弦长处, 圆柱直径D=0.1c, 二者展长均为l=300 mm。入口速度72 m/s, 噪声测试点位于翼型中心正上方1.85 m处。
|
| 图 4 模型示意图 |
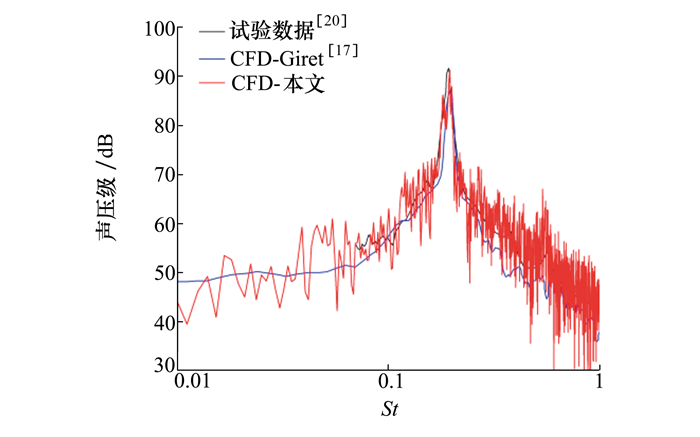
使用本文的数值方法对此模型进行了计算并与已发表试验数据[20]和仿真数据[17]进行对比, 结果如图 5所示。
|
| 图 5 数值方法验证结果 |
由图 5可以看出本文计算结果与已发表的试验结果和数值仿真结果在声压级曲线趋势和噪声峰值频率上基本一致, 因此本文的流场/声场混合计算方法得到了验证, 为后续的波状前缘降噪研究奠定了基础。
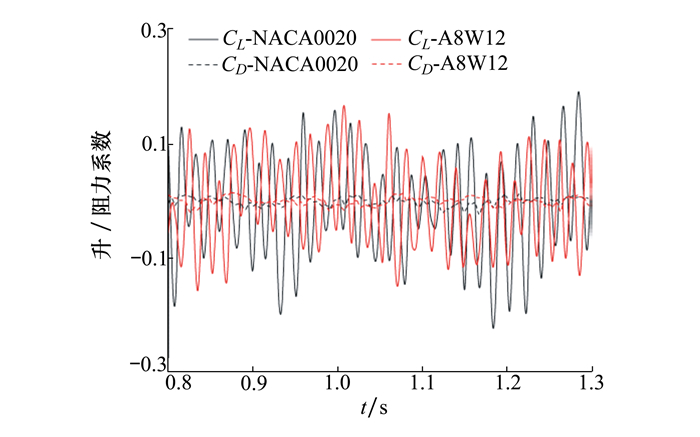
4 计算结果与分析 4.1 流场计算结果为研究波状前缘对翼型水动力性能的影响, 图 6给出了添加波状前缘前后的翼型升阻力系数时域曲线。由图可以看出波状前缘翼型和基础翼型的升阻力系数均在一定范围内绕固定值上下波动, 波状前缘的添加对翼型的阻力系数和升力系数的均值影响不大, 但能减小升力系数脉动的幅值。
|
| 图 6 升阻力系数时间历程 |
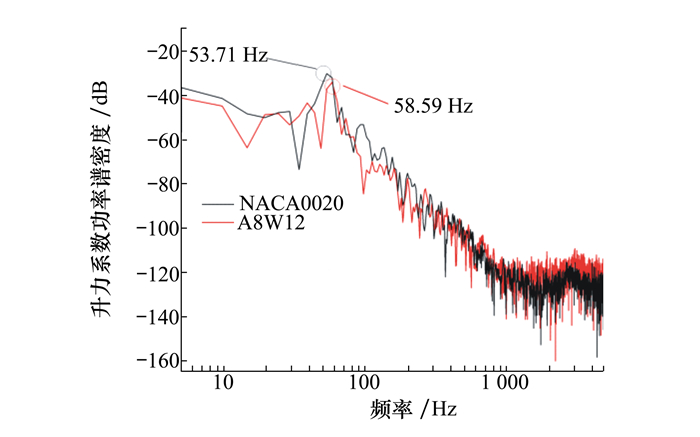
为进一步研究波状前缘对翼型升力系数的影响, 对NACA0020和波状前缘翼型A8W12的升力系数进行功率谱密度分析, 结果如图 7所示。可以看出波状前缘的添加降低了升力系数脉动幅值, 并且使得升力系数对应的特征频率后移, 原NACA0020的升力系数特征频率为53.71 Hz, 添加波状前缘后升力系数的特征频率变为58.59 Hz, 特征频率后移了4.88 Hz。
|
| 图 7 升力系数功率谱密度对比 |
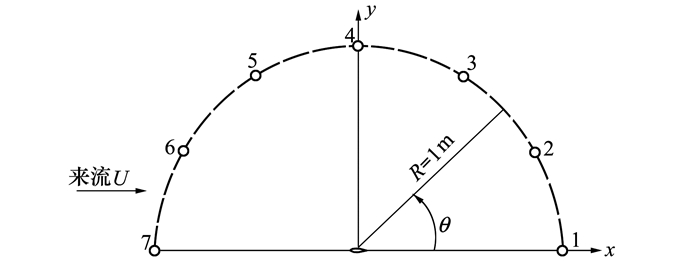
翼型噪声监测点的布置如图 8所示, 由于NACA0020和波状前缘翼型A8W12均为对称翼型, 本文计算为0°攻角, 因此只在其一侧布置监测点。本文监测点位于翼型中剖面z=21 mm,距翼型中心R=1 m处, 每隔30°布置一个。
|
| 图 8 翼型噪声监测点位置示意图 |
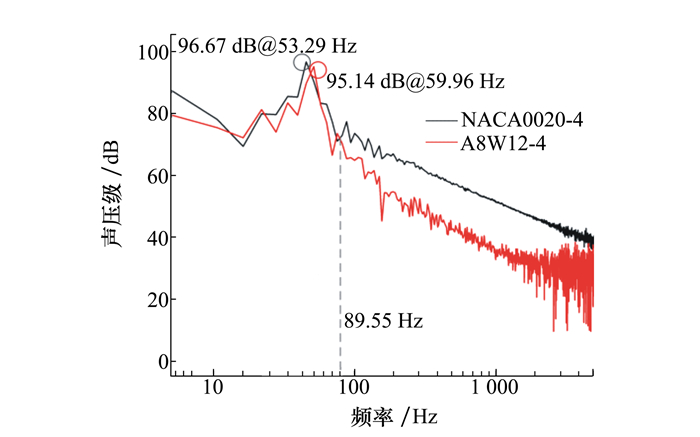
图 9为监测点4处的声压级频谱, 可以看出改型前后的翼型噪声都是由单音噪声(tonal noise)和宽频噪声(broadband noise)两部分组成, 单音噪声在低频有较高峰值。波状前缘的添加对声压谱曲线的曲线特征没有产生很大影响, 但使得声压级的大小尤其在中高频段有明显降低。波状前缘的添加使得原噪声谱的噪声峰发生了后移, 对于基础的NACA0020翼型, 其最大声压级为96.67 dB, 对应的峰值频率为53.29 Hz, 仿生翼型A8W12最大声压级为95.14 dB, 降低1.53 dB, 而对应频率为59.96 Hz, 后移了6.67 Hz。此外, 通过与图 7升力系数的功率谱密度进行比较可以发现, 声压级的峰值频率与升力系数的特征频率基本上相对应。波状前缘的添加虽没有明显降低翼型湍流干涉噪声的峰值, 但在89.55 Hz以后的中高频, 仿生翼型A8W12对其宽频噪声有显著降低效果, 降噪量在13 dB左右。
|
| 图 9 监测点4处声压级频谱图对比 |
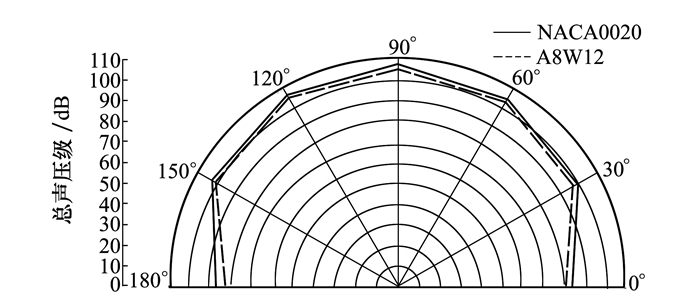
图 10为0~5 000 Hz下改型前后翼型的总声压级指向性对比图, 可以看出波状前缘的添加没有改变原翼型的声压级指向性特征, 二者都呈现出“8”字形的偶极子特征。但在各个监测点, 波状前缘均对翼型的总声压级产生了降低效果, 其中最大降噪量为4.35 dB。
|
| 图 10 总声压级指向性对比 |
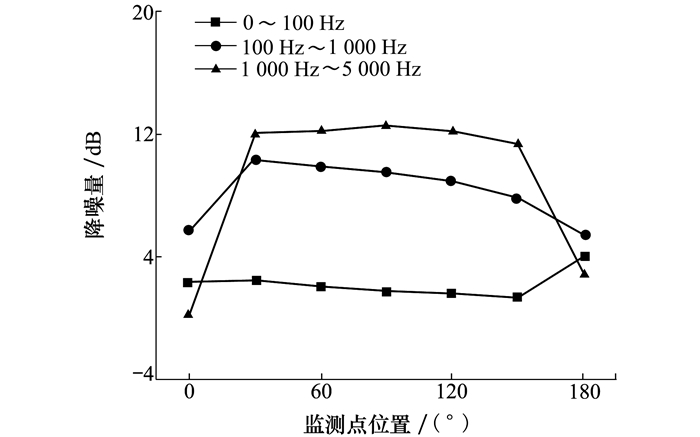
为了更好地分析波状前缘对翼型的降噪作用, 对0~5 000 Hz内2种翼型的噪声总声压级进行了分段计算, 各频段内的总声压级降噪量结果如图 11所示。在监测点1和7(即θ=0°和180°), 波状前缘在100~1 000 Hz频段内的降噪量最大, 分别为5.77 dB和5.51 dB, 在0~1 00 Hz频段内的降噪量次之, 在1 000~5 000 Hz频段内的降噪量最小。而对于监测点2~6, 波状前缘在1 000~5 000 Hz频段内降噪量最大, 最大降噪量达12.60 dB, 在100~1 000 Hz频段内的降噪量次之, 在0~100 Hz频段内的降噪量最小。波状前缘在各个监测点各个频段内的降噪量都为正值, 因此可以说波状前缘对翼型在本文所研究的工况下各个方向各个频率范围都能产生降噪作用。
|
| 图 11 各频段总声压级降噪量 |
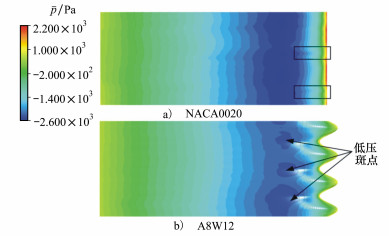
为了得出波状前缘的降噪机制, 对翼型湍流干涉流场进行了更为细致的分析。图 12所示为改型前后翼型吸力面的时均压力云图, 从图中可以看出波状前缘的添加减小了翼型沿前缘的压力值, 基础翼型NACA0020在前缘压力较高并且在展向变化小, 只有2处有明显展向压力变化, 而波状前缘翼型A8W12前缘的压力值无论是在波峰、波中还是波谷较基础翼型都有明显减小。此外波状前缘的添加使得在A8W12翼型的波谷后方产生了低压斑点, 即低压区主要集中在波谷后方而不是沿整个展向连续分布, 增大了翼型的展向压力梯度。
|
| 图 12 时均压力云图对比 |
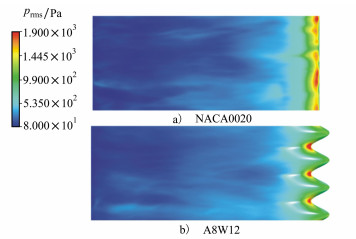
为进一步分析波状前缘对翼型表面压力带来的影响, 对图 13翼型表面压力脉动的均方根值进行了分析。波状前缘的添加将较高的压力脉动集中于波谷处, 使得其在波峰及中部位置明显降低。压力脉动的降低可以减小翼型的非定常载荷从而达到降噪效果。
|
| 图 13 压力脉动均方根云图 |
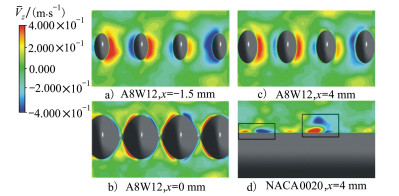
图 14给出了基础翼型NACA0020和波状前缘翼型A8W12不同y-z平面上的时均展向速度云图对比。来流湍流在经过NACA0020前缘后出现2处较明显的大小相反的展向速度, 与图 12中NACA0020表面压力变化位置一致。添加波状前缘后, 翼型展向速度不再是无规律变化, 而是呈现出了一定的规律性周期性, 在结节的两侧展向速度方向相反。
|
| 图 14 时均展向速度云图 |
图 15为翼型吸力面时均展向壁面剪切应力的对比图, 对于基础翼型NACA0020, 前缘主要存在2处展向壁面切应力较大的位置, 表明这两处有较强的展向流动, 与图 14相对应。对于波状前缘翼型, 展向壁面剪切应力分布有较强的规律性, 在每个波峰处有反向的展向壁面切应力, 在每个波谷处也有类似现象, 且波谷处值更大, 表明对于波状前缘翼型, 在波峰和波谷处均存在较强的展向流动, 这种分布与图 14中波状前缘的展向速度分布规律一致。

|
| 图 15 时均展向壁面剪切应力分布图 |
图 16给出了基础翼型和波状前缘翼型的涡核等值面图, 以流向涡量ωx着色。由图可以看出基础翼型的前缘涡结构在展向上连续性较强, 而波状前缘翼型的涡结构在展向上连续性减弱, 成为比较破碎的涡, 因此波状前缘可以减弱翼型前缘涡结构的相干性从而降低噪声。

|
| 图 16 涡核等值面图(Q=300 000) |
本文采用大涡模拟与FW-H方程相结合的方法研究了波状前缘对翼型湍流干涉噪声的影响。以NACA0020为基础翼型, 波状前缘采用正弦波, 幅值A=8 mm, 波长W=12 mm, 基于弦长c=100 mm的雷诺数为Re=3.05×105。首先采用LES方法对改型前后的翼型流场进行了计算, 而后基于获得的流场数据采用FW-H方程对翼型的远场干涉噪声进行了预报, 得到的结论如下:
1) 波状前缘的添加对翼型的气动性能造成了一定的影响, 降低了翼型升力系数脉动的幅值, 并使其特征频率发生了一定后移;
2) 添加波状前缘后翼型的噪声谱仍是由单音噪声和宽频噪声组成, 其单音噪声峰值有略微降低, 峰值频率与升力系数的特征频率对应, 也有一定后移, 而89.55 Hz后的宽带噪声则有显著降低。波状前缘的添加不会改变原翼型的总声压级指向性特征, 但在各个监测点均有一定的降噪效果。对不同频段总声压级进行计算后, 发现在1 000~5 000 Hz降噪量最大, 达12.60 dB。
3) 对波状前缘的降噪机理进行分析, 发现主要有两方面因素:①波状前缘翼型的压力脉动主要集中于波谷处, 在波峰和波中相对基础翼型压力脉动明显减小;②由于波状前缘的添加使得在翼型展向上流动增强, 涡的展向连续性减弱, 破碎成小涡, 从而降低了涡的展向相干性。
| [1] | FISH F E, BATTLE J M. Hydrodynamic design of the humpback whale flipper[J]. Journal of Morphology, 1995, 225(1): 51-60. DOI:10.1002/jmor.1052250105 |
| [2] | JOHARI H, HENOCH C W, CUSTODIO D, et al. Effects of leading-edge protuberances on airfoil performance[J]. AIAA Journal, 2007, 45(11): 2634-2642. DOI:10.2514/1.28497 |
| [3] | WEI Z, NEW T H, CUI Y D. An experimental study on flow separation control of hydrofoils with leading-edge tubercles at low Reynolds number[J]. Ocean Engineering, 2015, 108(1): 336-349. |
| [4] | PENA B, MUK-PAVIC E, THOMAS G, et al. Numerical analysis of a leading edge tubercle hydrofoil in turbulent regime[J]. Journal of Fluid Mechanics, 2019, 878: 292-305. DOI:10.1017/jfm.2019.611 |
| [5] | HANSEN K L, KELSO R M, DOOLAN C J. Reduction of flow induced tonal noise through leading edge tubercle modifications[C]//16th AIAA/CEAS Aeroacoustics Conference, 2010 |
| [6] | CHONG T, VATHYLAKIS A, MCEWEN A, et al. Aeroacoustic and aerodynamic performances of an aerofoil subjected to sinusoidal leading edges[C]//21st AIAA/CEAS Aeroacoustics Conference, 2015 |
| [7] |
石磊, 张成春, 王晶, 等. NACA0018翼型模型的仿生降噪[J]. 吉林大学学报, 2011, 41(6): 1664-1668.
SHI Lei, ZHANG Chengchun, WANG Jing, et al. Reduction of aerodynamic noise from NACA0018 airfoil model using bionic methods[J]. Journal of Jilin University, 2011, 41(6): 1664-1668. (in Chinese) |
| [8] | GRUBER M, JOSEPH P, POLACSEK C, et al. Noise reduction using combined trailing edge and leading edge serrations in a tandem airfoil experiment[C]//18th AIAA/CEAS Aeroacoustics Conference, 2012 |
| [9] | CLAIR V, POLACSEK C, GARREC T L, et al. Experimental and numerical investigation of turbulence-airfoil noise reduction using wavy edges[J]. AIAA Journal, 2013, 51(11): 2695-2713. DOI:10.2514/1.J052394 |
| [10] | PARUCHURI C C, NARAYANAN S, JOSEPH P, et al. Leading edge serration geometries for significantly enhanced leading edge noise reductions[C]//22nd AIAA/CEAS Aeroacoustics Conference, 2016 |
| [11] | TURNER J M, KIM J W. On the universal trends in the noise reduction due to wavy leading edges in aerofoil-vortex interaction[J]. Journal of Fluid Mechanics, 2019, 871: 186-211. DOI:10.1017/jfm.2019.314 |
| [12] | CHEN W, QIAO W, WANG X, et al. An experimental and numerical investigation of airfoil instability noise with leading edge serrations[C]//22nd AIAA/CEAS Aeroacoustics Conference, 2016 |
| [13] | CHEN W, QIAO W, DUAN W, et al. Experimental study of airfoil instability noise with wavy leading edges[J]. Applied Acoustics, 2021, 172(5): 107671. |
| [14] |
姜慧. 新型仿生螺旋桨水动力性能及噪声性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2016 JIANG Hui. Reaearch on hydrodynamic and noise performance of bionic propeller[D]. Harbin: Harbin Engineering University, 2016(in Chinese) |
| [15] | WANG M, FREUND J B, LELE S K. Computational prediction of flow-generated sound[J]. Annual Review of Fluid Mechanics, 2005, 38(1): 483-512. |
| [16] | CASALINO D, JACOB M, ROGER M. Prediction of rod-airfoil interaction noise using the Ffowcs-Williams-Hawkings analogy[J]. AIAA Journal, 2015, 41(5): 182-191. |
| [17] | GIRET J C, SENGISSEN A, MOREAU S, et al. Prediction of the sound generated by a rod-airfoil configuration using a compressible unstructured les solver and a FW-H analogy[C]//18th AIAA/CEAS Aeroacoustics Conference, 2012 |
| [18] | CHEN W, QIAO W, TONG F, et al. Numerical investigation of wavy leading edges on rod-airfoil interaction noise[J]. AIAA Journal, 2018, 56(7): 2553-2567. DOI:10.2514/1.J055825 |
| [19] |
汤渭霖, 俞孟萨, 王斌. 水动力噪声理论[M]. 北京: 科学出版社, 2019.
TANG Weilin, YU Mengsa, WANG Bin. Theory of hydrodynamic noise[M]. Beijing: The Science Publishing Company, 2019. (in Chinese) |
| [20] | JACOB M C, BOUDET J, CASALINO D, et al. A rod-airfoil experiment as a benchmark for broadband noise modeling[J]. Theoretical & Computational Fluid Dynamics, 2005, 19(3): 171-196. |
2. Key Laboratory of Unmanned Underwater Vehicle Technology, Northwestern Polytechnical University, Xi'an 710072, China




