2. 西北工业大学 航天学院, 陕西 西安 710075;
3. 西安现代控制技术研究所, 陕西 西安 710065
实弹飞行试验是装备鉴定/定型试验检验、考核的最终手段,但随着武器装备单子样价格的日益昂贵,现场实弹飞行试验样本越来越少,若单纯依据现场试验进行装备鉴定/定型评估风险增大。除实弹飞行试验外,仿真试验是装备鉴定/定型工作最重要的试验手段[1]。实践证明,在装备鉴定/定型工作中综合应用仿真技术,能够有效提高装备鉴定/定型质量、节省试验经费、缩短试验周期。
与实弹试验不同,仿真试验是基于模型的活动[2-4],仿真模型可信度是仿真手段在装备鉴定/定型应用中的生命线。目前要检验仿真模型可信度,最基本、最直接的方法是比较相同输入条件下飞行试验数据和仿真数据的一致性[4]。动态数据一致性检验方法主要有灰色关联分析、TIC、相关系数法、误差分析法、谱分析方法等[3],这些方法原理简单,计算易操作,但应用在装备鉴定/定型工作时仍存在一些不足,主要是:这些方法仅适应单样本(一维)试验数据之间的一致性检验[5-8],而装备鉴定/定型模型验证要检验单样本(一维)飞行试验数据与多样本(多维)仿真数据的一致性。现有文献[3-8]主要研究提高单样本参考数据和单样本比较数据的一致性检验精度和可靠性,并不适合解决装备鉴定/定型面临的单样本实弹飞行数据和多样本仿真数据这一类数据一致性检验问题。
针对上述问题,本文提出了一种基于概率关联分析的仿真模型验证方法。建立的概率关联度模型和概率关联分析方法,实现了由序列曲线关联向立体面板关联的方法拓展。建立的基于概率关联分析的仿真模型验证方法,解决了现有模型验证方法应用时数据利用不充分、验证算法不合适的问题。通过数值测试和应用实例验证了本文方法的正确性和有效性。
1 问题描述与分析在装备鉴定/定型试验中,分别获取了实弹飞试验数据X(i)(t), i=1, 2, …, m和仿真数据y (i)(t), i=1, 2, …, n, 其中, 上标i为第i次试验; m为实弹飞行试验次数; n为仿真试验次数。根据试验特点和数据来源,分析如下:
受试验消耗、试验周期等限制, 尤其是价格昂贵的导弹类装备鉴定/定型试验中, 现场实弹飞行科目设置时, 1组试验条件组合仅设置少量甚至1发导弹进行实弹试验, 实弹飞行试验数据X是小样本甚至是单样本。此外实弹飞行试验均是在确定性试验条件下进行, 但是确定性试验条件(如射向、射角、射程、目标特性、使用环境、作战方式等)仅是决定飞行试验数据状态的部分因素, 大量随机因素(如测试误差、器件误差、非线性误差和漂移、安装误差、延时误差、质心误差等)同时也是决定飞行试验数据状态的重要因素, 实弹飞行试验数据X包含随机因素的影响效应不全面。仿真技术具有经济性、方便性和可重复性等优势, 使得在相同组合试验条件下可以进行大量重复试验, 仿真试验数据y是大样本, 同时仿真试验数据y还包含有大量随机因素对试验数据状态的影响信息。
根据上述分析, 试验数据的特点是: 一般地, 在一类试验条件下, 实弹飞行试验数据X是单样本数据, 极少情况下是多样本数据; 仿真试验数据y在这一类试验条件下是多样本数据。因此, 装备鉴定/定型模型验证要解决的问题是: 通过检验单样本(维数=1)实弹试验数据X和多样本(维数>1)仿真数据y的一致性, 判断仿真系统是否可信。
2 现有模型验证方法缺陷动态数据一致性检验统一描述为2个步骤:
步骤1 计算k时刻关联系数, 算子如下所示
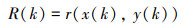
|
(1) |
式中: x, y为时间序列;r( · )为关联系数计算函数; R(k)为k时刻关联系数; k为时刻, k=1, 2, …, T, T为时间序列长度。
步骤2 计算综合关联度, 算子如下所示
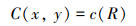
|
(2) |
式中: c( · )为综合关联度计算函数; C(x, y)为综合关联度; R为关联系数。
(1) 式、(2)式便完成了动态数据的一致性检验, 目前常见的动态数据一致性检验方法汇总见表 1所示。
| 序号 | 方法 | 关联系数计算 | 关联度计算 |
| 1 | 灰色关联分析 | 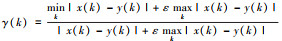 式中: ε为分辨系数, 在[0, 1]之间取值, 一般取0.5。 式中: ε为分辨系数, 在[0, 1]之间取值, 一般取0.5。 |
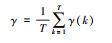 |
| 2 | TIC |  |
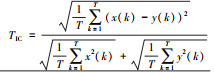 |
| 3 | 相关系数法 | 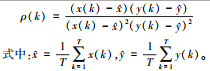 |
 |
| 4 | 误差分析法 | 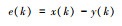 |
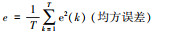 |
由表 1可知, 现有动态数据一致性检验方法能够直接处理单样本(一维)参考序列与单样本比较序列之间的一致性问题, 当检验数据为多样本(多维)序列, 或参考序列和比较序列其一是多样本序列时, 传统算法会得到多个关联度计算结果, 如何综合应用多个关联度结果是一个亟待解决的新问题。而装备鉴定/定型模型验证是检验单样本(一维)实弹飞行试验数据x和多样本(多维)仿真数据y的一致性, 因此表 1中的方法无法直接使用。如果选取多样本仿真数据中的一条进行分析, 势必造成试验信息浪费, 模型验证结果不充分。同时,若逐一关联分析多样本仿真数据后,如何应用出现的多个关联度也是一个难题。
3 概率关联度及基本性质 3.1 概率关联度为解决单样本实弹飞行数据和多样本仿真数据的一致性检验问题, 提出了概率关联度模型, 在数据关联分析时能够同时处理多样本序列, 避免了现有方法抽取多样本比较序列中的1条进行分析的不足,拓展了数据关联分析的应用领域。
为便于描述, 首先引入几个引理。
引理1 设X是一连续随机变量, 其分布函数为F(X), 则F(X)服从[0, 1]上的均匀分布。
引理2 设X、Y是不相关的连续随机变量, 其分布函数分别为F(X)、G(Y), 则[F(X)、G(Y)]服从[0, 1]上的二维均匀分布。
引理3 设xi为来自N(μi, σi2)正态分布簇的样本, p(xi)=F(xi)为其累积分布概率值, 则p服从[0, 1]上的均匀分布。
根据以上3个引理得到如下结论:
假设有2组数据
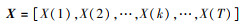
|
和
FY(k)为由数据Y(k)=[Y1(k), Y2(k), …, Yn(k)]T确定的概率分布函数, p(X(k))=FY(X(k))为X(k)的累积分布函数值, 若2组数据X与Y一致, 则有p(X(k)), k=1, 2, …, T服从[0, 1]上的均匀分布, 其中, T为数据序列长度。
根据上述结论, 单样本实弹飞行数据Y和多样本仿真数据Y的一致性检验可以转换为如下数学问题的求解: 判断p(X(k)), k=1, 2, …, T是否服从[0, 1]上的均匀分布, 若p(X(k))服从[0, 1]上的均匀分布, 则仿真模型通过验证; 否则未通过验证。
根据以上分析, 提出了概率关联度, 具体归纳为:
假设有参考序列x和比较序列y, 按照以下步骤计算参考序列x和比较序列y的概率关联度。
步骤1 计算k时刻概率关联系数poperator(k), 算子如下所示
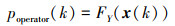
|
(3) |
步骤2 步骤计算概率关联度p, 算子如下所示

|
(4) |
式中: FY( · )为由y(k)确定的概率分布函数; FY(x(k))为x(k)在分布函数FY( · )中的累积概率分布函数值; c( · )为概率关联度模型中的综合概率度计算公式, 取均匀检验结果, 工程实现时可以调用chi2gof函数。
3.2 概率关联度的矩阵型数据应用改进假设参考数据x为多样本数据, 即

|
(5) |
为了计算矩阵型(多样本)参考序列x和矩阵型比较序列y的概率关联度, 对(3)~(4)式描述的概率关联度模型改进如下:
步骤1 计算k时刻的概率关联系数pi, operator(k), i=1, 2, …, m, 算子如下所示

|
(6) |
步骤2 计算概率关联度p, 算子如下所示
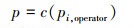
|
(7) |
(6)~(7)式中符号含义同(3)~(4)式。
3.3 概率关联度的性质定理1 概率关联度具有以下基本性质。
1) 规范性, 即0≤p(x, y)≤1;
2) 整体性, 对于不同的相关因素序列xi, xj, 一般有p(xi, xj)≠p(xj, xi), i≠j;
3) 可比性和唯一性;
4) 干扰因素独立性。
证明
1) 根据(4)式、(7)式所示概率关联度定义, 其内涵描述的是T个概率关联系数服从[0 1]均匀分布概率, 其值范围为[0 1], 故有0≤p(x, y)≤1。
2) 若xi, xj∈x={xS|s=0, 1, …, m; m≥2, 对于任意xS1, xS2, 一般由xS1, xS2确定的分布函数FxS1, FxS2不同, 有FxS1(x(k))≠FxS2(x(k)), 即p(xS1(k), xS2(k))≠p(xS2(k), xS1(k))成立, 故模型满足整体性。
3) 由于p(x, y)计算公式中不含有其他未知参数, 因此具有唯一性和可比性。
4) 由于p(x, y)的计算过程, 只与数据x和y有关, 与其他因素无关, 因此具有干扰因素独立性。
定理2 概率关联度不满足偶对称性, 即χ={ x, y }, 有p(x, y)≠p(y, x)。
证明 分别将x, y作为参考序列, 根据整体性性质推导过程, 一般有p(X(k), y(k))≠p(y(k), X(k))成立, 故概率关联度不满足偶对称性。
定理3 概率关联度模型不满足数乘变换一致性和平移变换一致性。
证明 对y分别作数乘变换和平移变换得y′ =c y, y″ =y+c。很显然, 由y确定的分布函数Fy与y′, y″确定的分布函数Fy′, Fy″一般并不一致, 故x在y, y′, y″确定的分布函数中的累积分布概率值不同, 故p(x, y)≠p(X, cy), p(x, y)≠p(x, y +c), 即概率关联度对数乘变换和平移变换均敏感, 不满足数乘变换和平移变换一致性。
4 基于概率关联分析的仿真模型验证方法 4.1 基本步骤步骤1 在相同初始条件下, 分别得到实弹飞行试验数据x和仿真试验数据y。
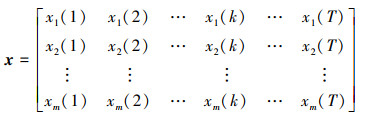
|
(8) |
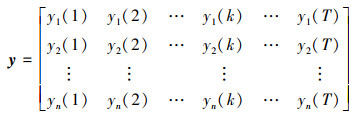
|
(9) |
式中: m为飞行试验样本量, 当m=1时为单样本实弹数据; n为仿真试验样本量; T为数据序列长度。
步骤2 对飞行试验数据x和仿真试验数据y进行预处理, 使其满足等步长、等长度的数据序列要求。
步骤3 计算k时刻由仿真试验数据y(k)确定的分布函数FY(k)。
步骤4 计算k时刻飞行试验数据X(k)在FY(k)中的累积分布函数值p(k)=FY(X(k))。
步骤5 检验p在一定置信水平α下是否服从[0, 1]上的均匀分布。
步骤6 若p服从[0, 1]上的均匀分布, 则模型通过验证。否则模型未通过验证, 需进行仿真模型修正后, 重新进行仿真模型验证。
4.2 优势分析1) 在关联系数计算时可以同时处理多样本仿真数据, 有效综合了系统随机效应影响, 此外对实弹飞行数据也没有维度限制(单样本或多样本均可), 这正是本文方法区别于灰色关联分析、TIC、谱分析、误差分析法等现有方法的主要优势, 也是本文方法的核心进步点和创新点。
2) 因仿真步长和外测设备测试步长一般在0.02~0.04 s, 因此试验数据序列长度T一般会较大, 参与本文方法中均匀分布检验的数据量很大, 均匀性检验结果是稳定的, 具有统计意义。
3) 灰色关联分析关注曲线几何形状相似性、TIC、相关系数关注曲线距离、谱分析关注数据频域组成与分布, 而本文方法关注参考数据与比较数据是否来源于同一随机过程, 更符合实际情况。
5 数值测试 5.1 场景描述为了检验本文方法的有效性, 选取几个典型案例进行了试验测试。测试过程如下:
步骤1 假定真实分布为F(x), 从真实分布F(x)中直接抽取样本x(i)(t)模拟实弹飞行数据, 其中i=1, 2, …, m, m为样本量, t为飞行时间。
步骤2 假定仿真试验误差为dF(y), 用G(y)=F(x)+dF(y)模拟仿真试验分布, 从G(y)中抽取样本y(i)(t)模拟仿真试验数据, 其中i=1, 2, …, n, n为样本量。很显然, 当dF(y)=0时, 仿真试验分布与真实分布相同。
步骤3 给出如下假设: 当dF(y)∈ε时, 仿真模型满足使用要求, 其中ε为根据试验要求确定的分布误差阈值限, 一般根据具体工程背景确定。
有效性测试判据为: 当dF(y)∈ε条件满足时, 根据实弹数据x和仿真数据y给出仿真模型有效, 即分布F(x)与G(y)一致; 否则, 当dF(x)ε时, 给出分布F(x)与G(y)不一致。
5.2 数值测试及结果分析试验1 平稳随机过程测试试验
用F(t)=N(0, 1)模拟实弹飞行抽样过程, 用S(t)=N(0+dμ, 1+dσ)模拟仿真抽样过程, 取t=15 s, 采样周期设置为dt=0.02 s, 同时取m=1, n=100。
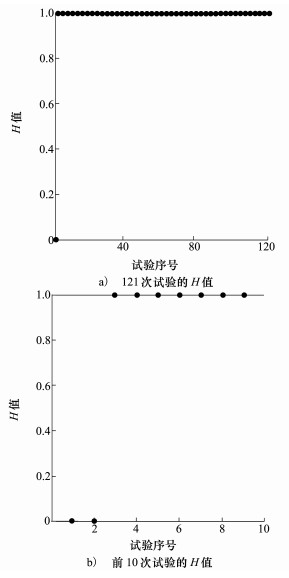
图 1给出了dμ=0∶0.1∶1, dσ=0∶0.1∶1时各种条件组合下121次仿真模型验证结果示意图, 数值测试中, 调用chi2gof函数(取α=0.05)检验概率关联系数是否服从[0 1]上的均匀分布。结果描述中, H表示仿真模型验证结果(chi2gof函数的计算返回值), 当H=0时, 表示模型通过验证; 当H=1时, 表示模型未通过验证。从图 1可见, 随着dμ, dσ逐渐增大(仿真系统可信度降低)时, 本文方法给出了模型未通过验证的结论, 说明本文方法的有效性。
|
| 图 1 H值(α=0.05) |
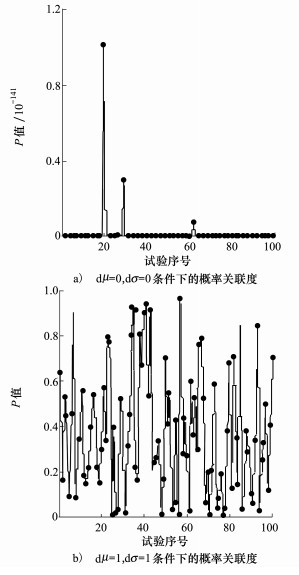
为了测试本文方法的稳定性, 分别选取dμ=0, dσ=0和dμ=1, dσ=1 2种场景, 进行100次Monte Carlo试验。图 2给出了100次Monte Carlo试验后的概率关联系数p(k)。从图 2可见, 本文方法能够正确给出模型验证通过和未通过的结论。在dμ=0, dσ=0试验中, 概率关联度p均非常小, H=0。在dμ=1, dσ=1的条件下, 给出了96次H=1的结果, 说明本文方法检验的稳定性。
|
| 图 2 100次Monte Carlo试验结果(α=0.01) |
试验2 非平稳随机过程测试试验
用以下非平稳随机过程场景进行测试。
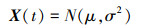
|
(10) |
式中: μ=20-0.001(0.2t-80)2; σ2=1。随机过程X(t)均值μ(t)与t相关。
从X(t)直接抽样模拟实弹数据, 从以下随机过程抽样模拟仿真数据。
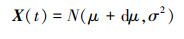
|
(11) |
式中: 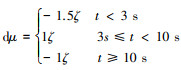
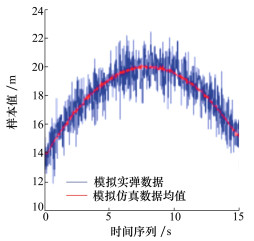
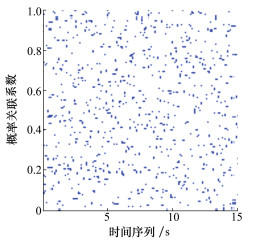
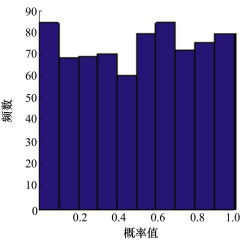
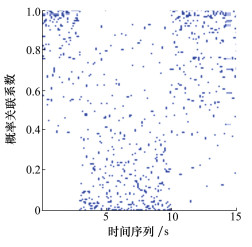
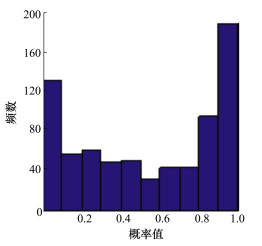
图 3给出了ζ=0时的实弹数据和仿真数据。图 4给出了ζ=0时的概率关联系数p(t)点图。图 5给出了ζ=0时的概率关联系数p(t)的频率图。图 6给出了ζ=1时的实弹数据和仿真数据。图 7给出了ζ=1时的概率关联系数p点图。图 8给出了ζ=1时的概率关联系数p(t)的频率图。从图 4、图 5可见, 实弹数据和仿真数据来源于同一非平稳随机过程X(t)时, 概率关联系数p(t)均匀性很好。从图 7、图 8可见, 当实弹数据和仿真数据来源分布不一致时, 概率关联系数p(t)均匀性较差, 说明本文方法能够处理这种情况, 给出正确的判断。
|
| 图 3 测试数据 |
|
| 图 4 ζ=0时概率关联系数q |
|
| 图 5 ζ=0时的概率关联系数频谱图 |

|
| 图 6 测试数据 |
|
| 图 7 ζ=1时概率关联系数 |
|
| 图 8 ζ=1时的概率关联系数频谱图 |
为了测试本文方法对非平稳随机过程检验的稳定性, 对2种场景分别进行100次Monte Carlo试验。图 9给出了100次Monte Carlo试验后的概率关联度p。从图 9可见, 本文方法能够正确给出非平稳随机过程条件下模型验证通过和未通过的结论。

|
| 图 9 100次Monte Carlo试验结果 |
试验3 非高斯随机过程测试试验
用以下非高斯随机过程场景进行测试。
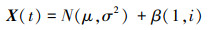
|
(12) |
式中: μ=20 - 0.001(0.2t-80)2; σ2=1;i=t/0.02。
从X(t)直接抽样模拟实弹数据, 从以下随机过程抽样模拟仿真数据。
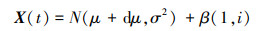
|
(13) |
式中: 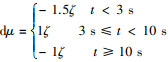
选取2种场景分别进行100次Monte Carlo试验。图 10给出了部分实弹数据和仿真数据。图 11给出了100次Monte Carlo试验后的概率关联度p以及仿真模型验证结果的H值图谱。从图 11可见, 本文方法能够正确的给出非高斯随机过程条件下模型验证通过和未通过的结论, 说明本文方法对非高斯随机过程数据一致性检验适应。
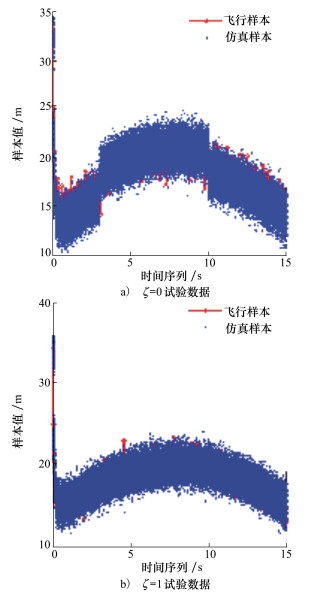
|
| 图 10 测试数据 |
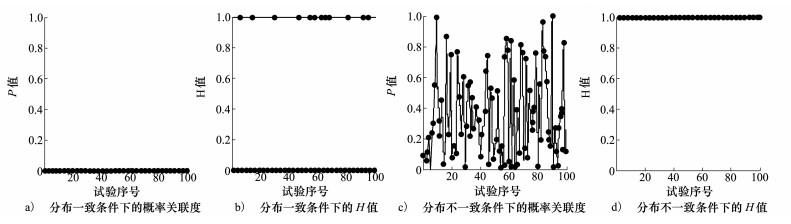
|
| 图 11 100次Monte Carlo试验结果 |
试验4 对比测试试验
通过对比测试试验分析本文方法与现有检验方法的性能, 试验场景同试验1。进行200次试验, 模拟仿真抽样样本量为100, 试验时参数设置为:
FOR i=1~200
dμ=(i-1)/60; dσ=(i-1)/60
END
图 12给出了各种检验方法的检验结果。从图 12可见, 灰色关联分析方法、相关系数方法、TIC方法、MSE方法给出了由100条曲线组成的曲面, 这是因为根据这些方法的定义, 分别计算了1组参考模拟数据和100组仿真数据的每一条数据的关联分析结果, 而本文方法给出的是一条关联曲线结果, 可见本文方法可以同时处理全部多组仿真数据。

|
| 图 12 不同方法的一致性检验结果 |
上述4个试验从不同视角测试了本文所提概率关联分析方法的有效性和正确性, 分析上述试验结果可得: 本文方法可以处理平稳随机过程数据、非平稳随机过程数据、非高斯过程数据等问题情景, 说明本文方法适应性广泛, 对数据特征基本不做要求, 使用时不必对数据提前做平稳性、高斯分布等假设; 本文方法可以直接处理单样本数据与多样本数据的一致性检验问题; 随着仿真模型可信度的降低, 本文方法能够正确给出定性的验证结果。
6 应用实例应用飞行试验数据验证某型反坦克导弹发动机的数字仿真模型。由于发动机推力在导弹飞行试验中无法直接测试, 我们通过导弹飞行试验V-T数据和仿真试验V-T数据的一致性检验验证发动机模型。
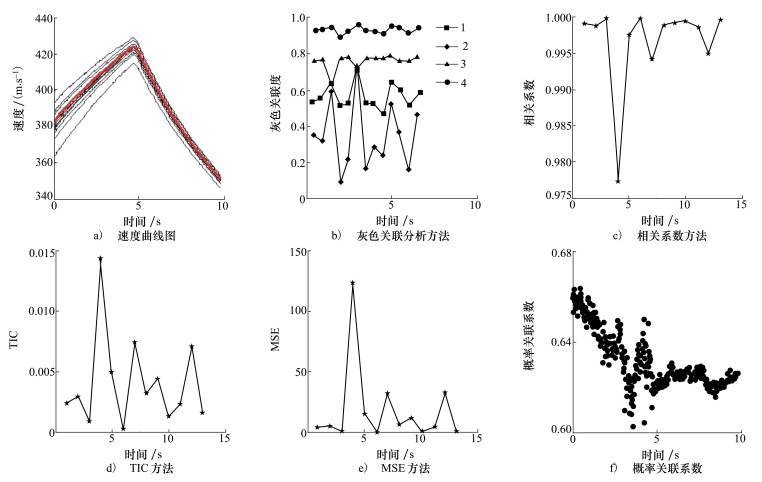
试验获取了1次飞行试验V-T数据和13次仿真试验V-T数据, 见图 13a)所示, 其中红色曲线为1次飞行试验V-T数据, 黑色曲线为13次仿真试验V-T数据。图 13b)至13e)给出了灰色关联分析(序号含义同文献[3])、相关系数法、TIC、MSE方法的检验结果。图 13f)给出了概率关联分析检验时的概率关联系数图, 显著水平取α=0.05, H的返回值为1, 表示拒绝原假设, 模型未通过验证。分析原因, 从图 13可见, 仿真试验V-T数据呈现一定的平行性, 这并不符合实际情况。
|
| 图 13 不同方法的检验结果 |
从图 13可见, 由于有13条仿真试验V-T数据, 灰色关联分析、相关系数法、TIC、MSE方法等现有方法均给出了13个关联计算结果, 但如何综合应用分析却未给出策略, 这也是这些方法在面向装备鉴定/定型模型验证应用时存在的不足。假设给定了判断阈值, 由于13个计算结果中有最大值和最小值, 若出现判断阈值介于最大值和最小值之间, 将出现无法判断的情况。本文方法由于关联系数计算时, 能够同时处理13条仿真试验数据, 直接给出了验证结论, 此时H=1, 模型未通过验证。
7 结论本文面向装备鉴定/定型应用的实际需求,针对装备鉴定/定型试验数据呈现的多维特点,提出了概率关联度模型和基于概率关联分析的仿真模型验证方法。该方法能够同时处理多样本仿真数据,解决了装备鉴定/定型工作中面临的单样本实弹飞行数据和多样本仿真数据这一类一致性检验问题。在计算时融合了试验过程的随机因素,在小样本实弹飞行试验条件下更能充分利用试验信息,克服了现有方法验模时数据利用不充分、验证算法不合适的不足。最后通过不同场景的数值测试和应用实例验证了本文方法的合理性和有效性。
| [1] |
张培忠. 制导炸弹仿真试验技术[M]. 北京: 国防工业出版社, 2019.
ZHANG Peizhong. Guided bomb simulation test technology[M]. Beijing: National Defense Industry Press, 2019. (in Chinese) |
| [2] |
李伟, 焦松, 陆凌云, 等. 基于特征差异的仿真模型验证及选择方法[J]. 自动化学报, 2014, 40(10): 2134-2144.
LI Wei, JIAO Song, LU Lingyun, et al. Validation and selection of simulation model based on the feature differences[J]. Acta Automatica Sinica, 2014, 40(10): 2134-2144. (in Chinese) |
| [3] |
宁小磊, 吴颖霞, 于天朋, 等. 基于改进灰色关联分析的仿真模型综合验证方法[J]. 兵工学报, 2016, 37(2): 338-347.
NING Xiaolei, WU Yingxia, YU Tianpeng, et al. Research on comprehensive validation of simulation models based on improved grey relational analysis[J]. Acta Armamentarii, 2016, 37(2): 338-347. (in Chinese) DOI:10.3969/j.issn.1000-1093.2016.02.021 |
| [4] | LAILI Yuanjun, ZHANG Lin, LUO Yongliang. A pattern-based validation method for the credibility evaluation of simulation models[J]. Simulation: Transactions of the Society for Modeling and Simulation International, 2020, 96(2): 151-167. DOI:10.1177/0037549719856100 |
| [5] | CAMPOLI L, KUNOVA O, KUSTOVA E, et al. Models validation and code profiling in state-to-state simulations of shock heated air flows[J]. Acta Astronautica, 2020, 175(7): 493-509. |
| [6] | NAYLOR T H, FINGER J M. Verification of computer simulation models[J]. Management Science, 1967, 14(2): 92-101. DOI:10.1287/mnsc.14.2.B92 |
| [7] | LI W, CHEN W, JIANG Z, et al. New validation metrics for models with multiple correlated responses[J]. Reliability Engineering & System Safety, 2014, 127: 1-11. |
| [8] |
林圣琳, 李伟, 杨明, 等. 考虑相关性的多元输出仿真模型验证方法[J]. 自动化学报, 2019, 45(9): 1666-1678.
LIN Shenglin, LI Wei, YANG Ming, et al. Multivariate validation method under correlation for simulation model[J]. Acta Automatica Sinica, 2019, 45(9): 1666-1678. (in Chinese) |
2. College of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China;
3. Xi'an Modern Control Technology Research Institute, Xi'an 710065, China




