2. 陕西省飞行控制与仿真技术重点实验室, 陕西 西安 710129;
3. 中国航空工业成都飞机设计研究所, 四川 成都 610091
非线性动态逆(nonlinear dynamic inversion, NDI)是一种经典的非线性控制方法,该方法通过“反演求逆”的策略消除模型的非线性以及各通道之间的耦合,进而保证系统达到期望动态。得益于解耦能力强、快速性好的特点,该方法已经成功应用在战斗机[1-3]、无人机[4]等飞行器的控制律设计中。飞行器复杂的结构决定了实际中很难获取精确的气动参数,并且面对模型不确定性、外界扰动等因素的影响,该方法都暴露出鲁棒性不足的问题。部分学者采用增量式的动态逆(incremental NDI, INDI)的方法来提高飞控系统的鲁棒性[5-6]。但INDI中需要反馈角加速度信号,并且该信号的准确性直接关系到INDI控制的鲁棒性。然而实际飞机中并未配备角加速测量相关的传感器,取而代之的是采用对角速度差分滤波的方式获取角加速[7],这一过程中差分会放大残余噪声并且滤波产生的时延会不同程度破坏加速度的准确性和实时性,进而降低INDI的鲁棒性。因此,如何获取准确的角加速度信号这一实际难题阻碍了INDI方法在实际飞控系统设计中的应用。
将自适应控制策略加入到NDI控制系统同样能提高NDI控制的鲁棒性,此种类型的改进称之为自适应动态逆。自适应算法根据动态误差估计出不确定性和扰动对系统产生的影响,进而,控制器根据估计出的影响参数对系统进行修正纠偏。例如文献[8-9]通过在NDI控制中加入神经网络结构提高系统的鲁棒性。因此,在NDI控制中加入自适应结构可以增强NDI控制系统对干扰的鲁棒性。
L1自适应控制最早是由Cao等在2006年美国控制会议上提出的一种强鲁棒自适应控制方法[10]。该方法由模型参考自适应控制发展而来,在控制器中加入低通滤波器解决了传统自适应控制中高增益容易导致系统高频振荡的问题。L1自适应控制方法兼顾了响应的快速性和系统对模型不确定性、外界扰动等干扰影响的鲁棒性。因而该方法在提出后受到了国内外控制学者的广泛关注,并在诸多应用领域都获得了丰硕的研究成果[11-14]。Li等研究了基于分段常数的L1自适应多输入多输出控制方法,并且对分段常数算法进行了改进,提高了该算法的估计精度[11]。周艳等则是采用L1自适应控制解决了执行机构故障下飞行器的容错控制问题[12]。针对着舰中舰尾流干扰问题,L1自适应控制同样被应用于舰载机纵向和侧向自动着舰控制律设计中,抑制舰尾流等不确定性干扰,最终实现着舰轨迹的精确跟踪[13-14]。从所公开的研究成果来看,L1自适应控制方法能够有效克服扰动对系统的干扰影响,并且适合解决包含不确定因素和存在未建模动态等复杂系统的控制问题,因此该方法适合于飞行容错控制系统的设计。
从增强NDI控制鲁棒性的角度出发,本文将L1自适应结构引入到NDI控制中,提出一种基于L1自适应动态逆的控制方法,通过L1自适应结构消除不确定因素和干扰的影响。此外,基于此方法设计飞行控制律提高飞机的鲁棒性。研究成果对保证飞机安全飞行具有重要意义。本文的创新点主要有以下2个方面:
1) 在NDI控制中引入L1自适应控制结构,提出基于L1自适应结构的动态逆控制方法。该控制方法既保留了NDI快速解耦能力,又具有L1自适应控制优异的鲁棒性和快速自适应能力,因而能够削弱干扰等因素对系统的影响,实现提升NDI控制系统的鲁棒性的目标。
2) 理论分析了干扰影响下L1结构的自适应动态逆控制方法在Lyapunov意义下的稳定性,证明了该方法对扰动的鲁棒性。此外,还讨论了该控制器作用下系统状态的边界特性。
1 动态逆系统分析被控对象模型可以描述为
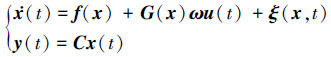
|
(1) |
式中: x(t)∈Rn是系统状态; f(x)∈Rn表示与控制无关的系统非线性矩阵; G(x)∈Rn×m, (m>n)表示系统的控制矩阵; ω∈Rm×m为符号已知大小未知且非奇异的对角矩阵, 表示不确定系的统控制效能矩阵; u(t)∈Rm是系统的控制输入; C∈Rm×n和y(t)∈Rm为系统输出矩阵和输出量。ξ(x, t)∈Rn表示未知的非线性干扰, 包括外部扰动、参数不确定以及未建模动态等所有干扰影响的综合。
由于受到实际因素的限制, 系统模型并不完全已知或者与真实值存在一定偏差。因此系统非线性项f(x)和G(x)可拆分为两部分
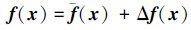
|
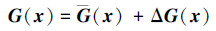
|
(2) |
式中, f(x)∈Rn和G(x)∈Rn×m表示已知系统的非线性函数, 可直接用于控制律设计; 而Δf(x)∈Rn和ΔG(x)∈Rn×m则表示与模型有关的不确定性, 因此无法直接获取。将被控对象进一步变型为
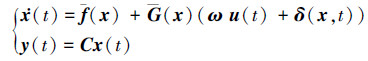
|
(3) |
式中, 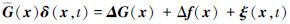
扰动满足以下假设:
假设1 扰动δ(x, t)全局有界并且零状态有界。即存在正常数B>0, 扰动满足
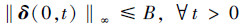
|
此外, 存在常数D>0和X>0, 使得扰动在任意时刻t>0且状态量有界‖x(t)‖∞≤X的范围内, 扰动满足‖δ(x, t)‖∞≤D。
假设2 扰动δ(x, t)偏导数存在且有界。存在常数dδ, t>0和dδ, t>0, 则扰动偏导数满足
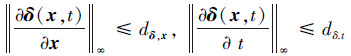
|
假设3 扰动δ(x, t)满足半全局Lipschitz条件。即对于任意ρ>0, 存在正常数Lρ>0, 使得
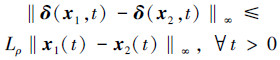
|
仿照参考文献[10], 结合以上假设, 可将非线性扰动δ(x, t)进一步转化为
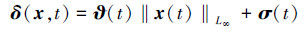
|
(4) |
式中, ϑ(t)∈Rm×n表示与状态量相关的干扰。而σ(t)∈Rm则表示时变干扰。此时被控对象变为
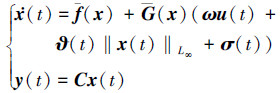
|
(5) |
由假设1和2可以知, ϑ(t)和σ(t)必然满足以下边界条件
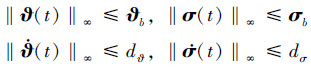
|
(6) |
在不考虑扰动影响且被控对象模型完全已知的情况下, 即δ(x, t)=0和ω=In。根据反馈线性化求逆的思想得到NDI控制律(7)。
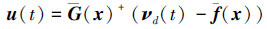
|
(7) |
式中, νd表示期望动态响应。此时, NDI控制律作用下系统动态为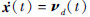
若考虑未建模、参数不确定等诸多干扰的影响, 系统的响应则变为
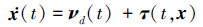
|
(8) |
式中
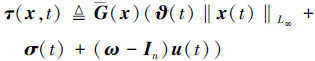
|
(9) |
在参数不确定以及扰动的影响下, 系统动态不再满足期望要求。扰动下NDI控制鲁棒性的缺失阻碍了该方法在实际中的应用。在提高NDI控制鲁棒性需求的牵引下, 本文提出一种鲁棒性强的自适应动态逆的控制方法, 称之为L1自适应动态逆控制。
2 L1自适应动态逆控制方法L1自适应动态逆控制方法兼顾了L1自适应控制和NDI控制的特点。其中, NDI控制部分用于消除系统已知的非线性部分, 而L1自适应控制则用于消除未建模动态、模型不确定性以及外部扰动的影响。本小节主要研究L1自适应动态逆控制方法, 旨在减小NDI控制方法对模型依赖的同时, 提高控制器对扰动影响的鲁棒性。
2.1 带有低通滤波器的控制律设计L1自适应动态逆控制器由状态预测器、自适应律和带有低通滤波器的动态逆控制律三部分组成。状态预测器输出具有系统状态期望动态, 自适应律则是根据系统响应与状态预测器之间的误差估计相关的扰动影响, 低通滤波器的控制律则在已知模型信息的基础上根据自适应律反馈的扰动估计参数对系统进行修正, 保证系统输出与状态预测器一致, 并且消除自适应估计的高频动态。
L1自适应动态逆控制信号u(t)包括两部分, 即动态逆控制uNDI(t)和L1自适应控制uL1(t)。
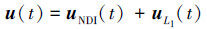
|
(10) |
NDI控制部分uNDI(t)用于消除被控对象中已知非线性的部分, 具体设计如下
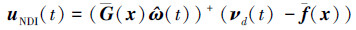
|
(11) |
式中虚拟控制量νd(t)设计为
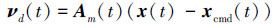
|
(12) |
式中:xcmd(t)为系统的输入指令; Am(t)∈Rn×n表示系统期望动态特性的Hurwize矩阵。
L1自适应控制部分uL1(t)则是用于消除各种扰动造成的影响, 进而补偿NDI控制鲁棒性的不足。具体设计如下
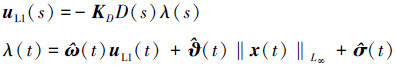
|
(13) |
式中, s表示Laplace算子。增益矩阵KD∈Rm×m和传递函数D(s)都是滤波器组成参数, 对应低通滤波器具体形式为
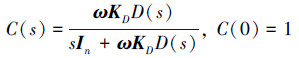
|
(14) |
由于扰动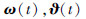
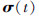
低通滤波器C(s)用于滤除律估计参数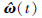
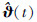
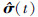
在控制律的作用下, 状态预测器具有系统所期望的动态, 实时为系统提供参考。具体设计如下
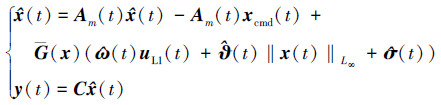
|
(15) |
式中, 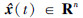
自适应律根据系统响应与状态预测器之间的误差实时更新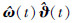
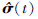
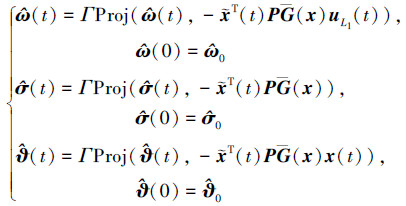
|
(16) |
在自适应律中, Proj(·, ·) 表示投影算子运算符, 具体详见参考文献[14]。Γ∈R+表示自适应增益。矩阵P是Lyapunov方程AmTP+PAm=-Q的解。e(t)表示状态预测器与系统之间的误差, 即
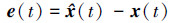
|
(17) |
由于该方法在NDI方法的基础上引入L1自适应结构, 因而解决了NDI控制方法依赖于模型参数信息以及在干扰影响下系统鲁棒性差的问题。
相比于传统自适应动态逆控制方法, L1自适应动态逆控制在保证扰动影响下系统的鲁棒性的同时, 通过引入低通滤波器解决了常规自适应因自适应增益过大而导致控制信号高频振荡的问题。进而缓和了常规自适应控制中鲁棒性和快速性之间的矛盾。
3 L1自适应控制系统性能分析本小节主要对L1自适应控制系统的稳定性和边界特性进行证明和分析。
3.1 稳定性证明在对L1自适应动态逆控制性能分析之前, 定义在分析过程中用到的一些误差参数
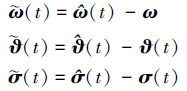
|
(18) |
其次, 结合(6)来定义边界Θ(ρ)
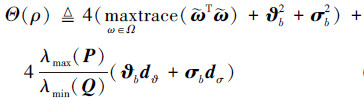
|
(19) |
根据(5)式、(10)式和(15)式, 可推导出跟踪误差的动态方程
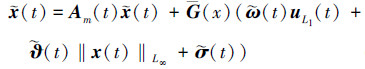
|
(20) |
选取Lyapunov函数
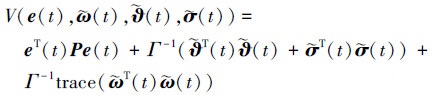
|
(21) |
初始时刻该函数满足
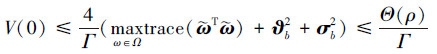
|
(22) |
结合误差动态方程(20), 可得到Lyapunov函数的导数, 具体过程如下
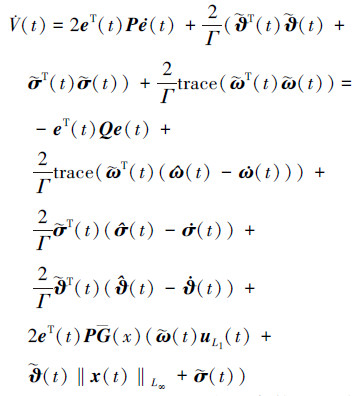
|
(23) |
对于Ɐt∈[0, τ1), τ1表示参数不连续的时刻。将投影算子自适应律(16)式代入(23)式可推出
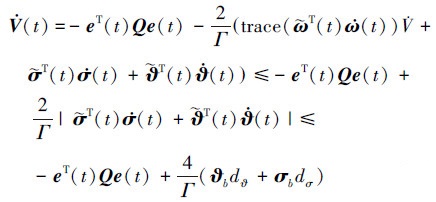
|
(24) |
由参数边界限制(6)能得到

|
(25) |
假设存在任意时间τ′∈(0, τ1)使得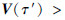
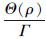
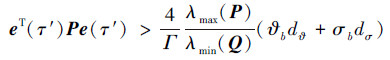
|
(26) |
根据矩阵特征值与范数之间的关系, 可得
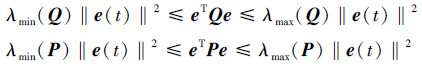
|
(27) |
因此
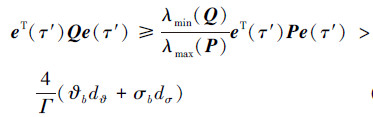
|
(28) |
结合(24)式, 可以看出在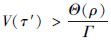
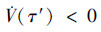
|
(29) |
所以, Lyapunov方程在所有时刻都满足
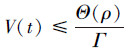
|
(30) |
由于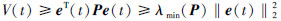
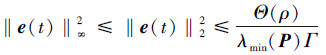
|
(31) |
综上所述, 系统跟踪误差的界为
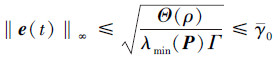
|
(32) |
式中, y0表示任意小的正常数。从(32)式能看出误差的上界与自适应增益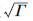
同样, 在分析边界特性之前, 首先定义以下几个转换矩阵
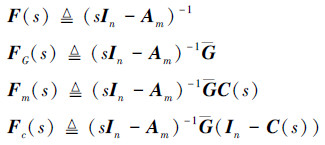
|
(33) |
引入非L1自适应动态逆控制的闭环参考系统来分析系统的边界特性, 具体如下
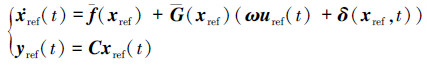
|
(34) |
与之对应的控制律如下
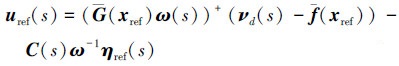
|
(35) |
式中, 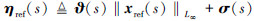
在参考模型控制律(35)式的作用下, 闭环参考系统状态的频域形式可表达为
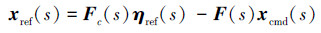
|
(36) |
结合扰动误差的定义(18), L1自适应动态逆控制器(10)可的频域形式为
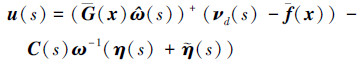
|
(37) |
式中
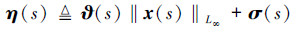
|
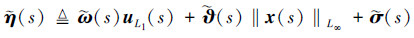
|
(38) |
此时, 实际系统(5)状态的频域形式为
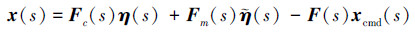
|
(39) |
则实际系统与参考系统状态误差为
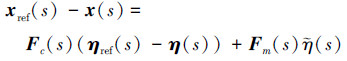
|
(40) |
根据系统误差方程(20)可推导出
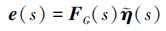
|
(41) |
因此, (40)式变为
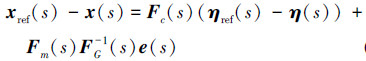
|
(42) |
那么
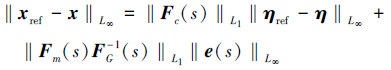
|
(43) |
根据假设3, 可以将(43)式进一步变型为
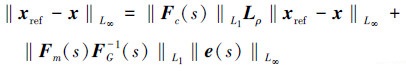
|
(44) |
结合系统跟踪误差的界(32)式、(44)式可最终化为
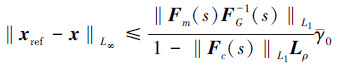
|
(45) |
进一步, 系统输出的边界特性为
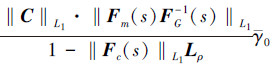
|
(46) |
(32) 式、(45)式和(46)式为系统的性能边界。从中能看出增加自适应增益Γ能够缩小实际系统与理想系统之间的界, 使得L1自适应动态逆控制控制作用下系统趋近于期望动态性能。而增大自适应增益Γ引起的振荡由控制律中低通滤波器来消除。
4 L1自适应动态逆角速度控制律设计以公开F-16飞机作为研究对象来验证所提出方法的控制性能。该机质量为9 295.44 kg, 翼面面积S为27.87 m2, 平均气动弦长c为3.45 m, 翼展b为9.144 m。可操纵面包括副翼δa, 全动平尾δe, 方向舵δr, 前缘襟翼δlef以及发动机。该机气动数据由NASA风动吹风得出, 具体详见文献[16]。
4.1 飞行器建模飞机角速度运动和侧滑角方程可写为
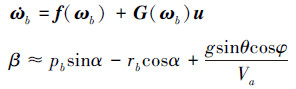
|
(47) |
式中
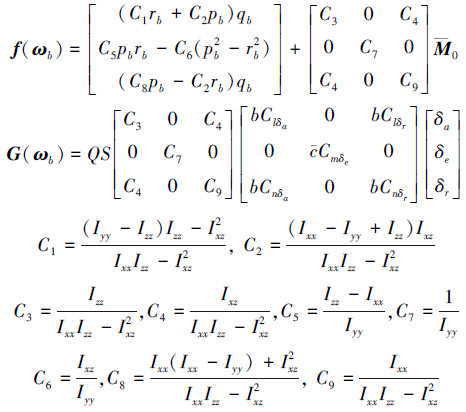
|
式中: ωb=[pb, qb, rb]T表示机体坐标系下的三轴角速度; I**表示飞机对应轴的转动惯量; Va为真空速, M=[L, M, N]T为总力矩; Q表示动压; M0是气动力产生的气动力矩; Clδa, Clδr, Cmδe, Cnδa, Cnδr为各控制面的操纵导数。
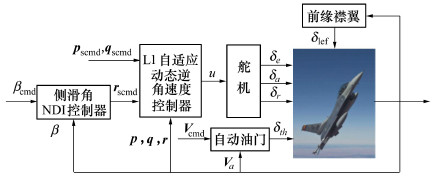
4.2 L1自适应动态逆控制器设计通常驾驶杆的纵轴和横轴指令对应飞机稳定坐标系下的俯仰角速度qs和滚转角速度ps, 脚蹬直接对应飞机侧滑角指令, 油门杆则用于控制速度。为了提高飞控系统的鲁棒性, 采用L1自适应动态逆方法设计角速度控制律、积分式NDI方法设计侧滑角控制律以及PI方法的自动油门控制律。整个控制结构框架如图 1所示:
|
| 图 1 F-16飞行控制整体结构 |
稳定系中角速度ps, qs, rs与机体系中角速度pb, qb, rb之间的关系如下
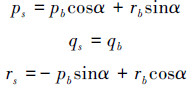
|
(48) |
根据(10), (15)和(16)式来设计L1自适应动态逆角速度控制器。其中控制器和低通滤波器相关参数具体如下
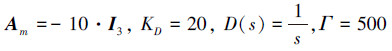
|
(49) |
基于积分式NDI的侧滑角控制律设计如下

|
(50) |
式中
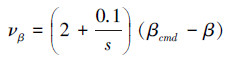
|
(51) |
采用简单的PI控制器设计自动油门控制器。该控制律据速度响应误差调整油门开度δth完成对飞机的速度控制, 具体设计为
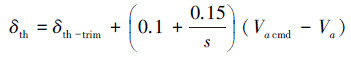
|
(52) |
在控制律中, δth-trim为配平的油门位置, 油门位置限制在0≤δth≤1。
前缘襟翼不作为直接操纵面对控制飞机, 其控制律根据状态自动生成, 具体如下
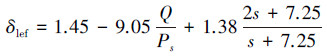
|
(53) |
式中: Ps为静压; α表示迎角。
用一阶惯性环节传递函数来模拟执行机构, 不同执行机构的幅度和速率的限制如表 1所示。
| 名称 | 幅度限制/(°) | 速率限制/((°)·s-1) |
| 副翼 | -21.5~21.5 | -80~80 |
| 升降舵 | -25~25 | -60~60 |
| 方向舵 | -30~30 | -120~120 |
| 襟翼 | 0~25 | -25~25 |
为了验证所提出的L1自适应动态逆方法的鲁棒性, 因此在故障干扰下对基于此方法设计的飞行控制器进行仿真, 并与NDI方法进行对比验证。
以下仿真都是在2 000 m高度, 150 m/s速度的巡航条件下完成, 飞机的巡航状态如表 2所示。
| 状态 | 配平值 |
| H/m | 2 000 |
| Va/(m·s-1) | 150 |
| p, q, r/((°)·s-1) | 0 |
| β, φ, ψ/(°) | 0 |
| α, θ/(°) | 3.56 |
| δe/(°) | -4.49 |
| δa, δr/(°) | 0 |
| δlef/(°) | 5.13 |
| δth-trim | 0.11 |
平飞过程中, 假设12秒飞机突发损伤故障, 损伤致使气动参数以及气动导数产生偏差, 具体变化详见表 3。这些由故障产生参数的偏差被控制器视为干扰。在损伤故障干扰下对基于L1自适应动态逆飞行控制器的鲁棒性进行验证, 仿真结果如图 2~5所示。
| 参数 | 故障参数变化 |
| S/m2 | 0.95 |
| /m | 0.95 |
| b/m | 0.9 |
| m/kg | 0.95 |
| Ixx/(kg·m2) | 0.9 |
| Ixz/(kg·m2) | 0.9 |
| xcg/m | xcg+0.2 |
| ycg/m | 0.1 |
| zcg | 0.15 |
| Cm | 0.8 |
| Cl | 0.8 |
| Cl | 0.9 |
|
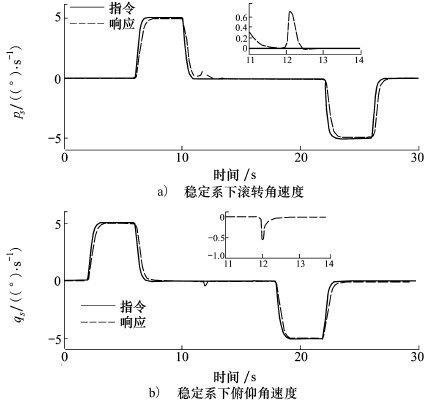
| 图 2 稳定系下的滚转俯仰和俯仰角速度响应曲线 |
|
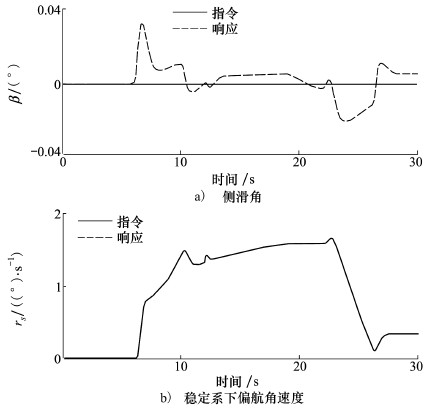
| 图 3 侧滑角和稳定系下偏航角速度响应曲线 |
|
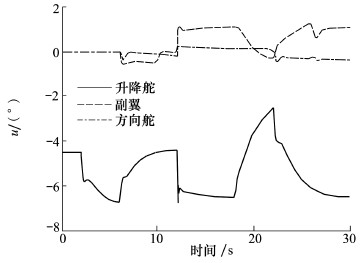
| 图 4 侧滑角和舵面偏转对比曲线 |
|
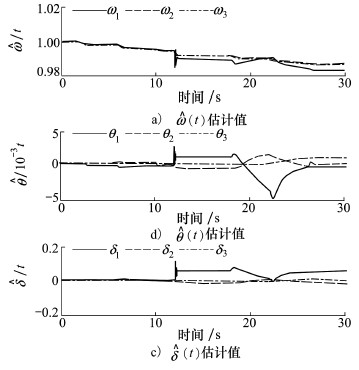
| 图 5 自适应律估计出扰动影响曲线 |
正常状况下,飞机能快速准确跟踪上所给指令信号。在12 s损伤发生后,飞机的状态出现突变,但在L1自适应动态逆控制器作用下,飞机迅速恢复平衡状态,并且在够保证飞机稳定性的同时,能克服故障造成的影响,后续的角速度响应依旧能达到故障前预期的动态。整个响应过程中侧滑角响应很小,可认为侧滑角基本保持在零,达到预期要求。仿真结果验证了理论推导,表明L1自适应动态逆控制器具有出色的鲁棒性。
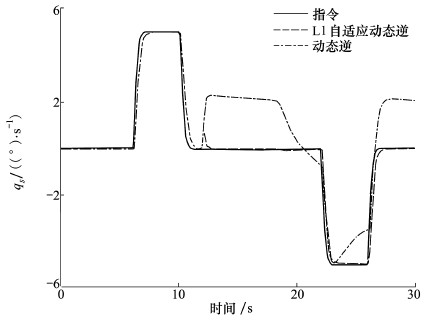
为了进一步突出鲁棒性,在相同的指令信号下对比验证常规NDI控制和L1自适应动态逆的控制效果。对比结果如图 6至8所示。
|
| 图 6 参数不确定扰动下,滚转角速度对比 |
|
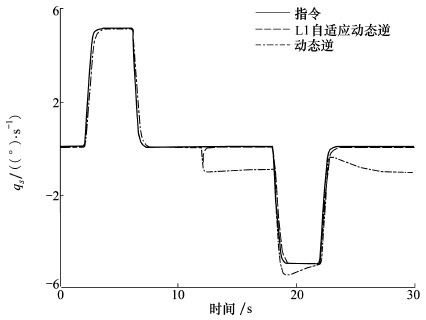
| 图 7 参数不确定扰动下,俯仰角速度对比 |
|
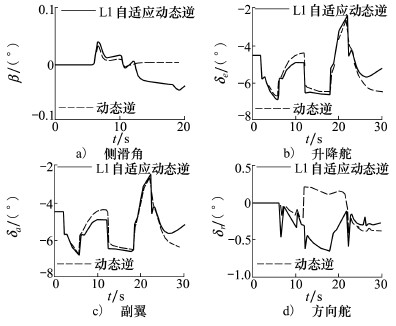
| 图 8 侧滑角和舵面偏转对比曲线 |
从对比结果能明显看出:由于正常情况下飞机的结构和参数完全已知,因此2种控制器都能达到期望的控制效果。故障的发生对飞机产生未知干扰并且造成模型参数的不确定变化,然而L1自适应动态逆控制结构中能感知、估计以及消除扰动和不确定性造成的影响,因此基于L1自适应动态逆飞行控制器对干扰具有鲁棒性。相反,NDI控制器过于依赖模型,并且没有补偿机制来克服不确定性影响,所以NDI控制器的控制性能在故障影响下出现降级,不再满足预期控制要求。
6 结论本文在常规NDI控制的基础上结合L1自适应结构,提出一种基于L1自适应动态逆的鲁棒控制方法来解决NDI方法在干扰情况下缺乏鲁棒性的问题。该方法能够快速地估计并消除扰动对系统造成的影响, 进而保证了干扰影响下系统的稳定性和鲁棒性。此外,该方法继承NDI控制快速解耦的能力,由于控制结构中含有低通滤波器,因而该方法避免系统因快速自适应而振荡,进而解决了系统响应快速性和鲁棒性之间不匹配的问题。最后,设计了基于L1自适应动态逆控制的飞行控制律并对其进行仿真,结果表明所设计的飞行控制器能够克服损伤故障造成的影响,并在损伤故障下依旧能够达到令人满意的控制性能。本文为提高飞行控制系统的鲁棒性做出一定的贡献。
| [1] | RICHARD Colgren, DALE Enns. Dynamic inversion applied to the F-117A[C]//Modeling and Simulation Technologies Conference, 1997 |
| [2] | MENON P P, LOWENBERG M H, HERRMANN G, et al. Experimental implementation of a nonlinear dynamic inversion controller with antiwindup[J]. Journal of Guidance Control and Dynamics, 2013, 36(4): 1035-1046. DOI:10.2514/1.59027 |
| [3] | LOMBAERTS Thomas, KANESHIGE John, SCHUET Stefan, et al. Dynamic inversion based full envelope flight control for an evtol vehicle using a unified framewor[C]//AIAA Scitech 2020 Forum |
| [4] | LUNGU M. Auto-landing of UAVs with variable centre of mass using the backstepping and dynamic inversion control[J]. Aerospace Science and Technology, 2020, 103: 105912. DOI:10.1016/j.ast.2020.105912 |
| [5] | SIMPLICIO P, PAVEL M D, VAN KAMPEN E, et al. An acceleration measurements-based approach for helicopter nonlinear flight control using incremental nonlinear dynamic inversion[J]. Control Engineering Practice, 2013, 21(8): 1065-1077. DOI:10.1016/j.conengprac.2013.03.009 |
| [6] | LU Peng, VAN KAMPEN Erikjan, DE VISSER Cornelis, et al. Aircraft fault-tolerant trajectory control using incremental nonlinear dynamic inversion[J]. Control Engineering Practice, 2016, 57: 126-141. DOI:10.1016/j.conengprac.2016.09.010 |
| [7] | SIEBERLING S, CHU Q P, MULDER J A, et al. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction[J]. Journal of Guidance Control and Dynamics, 2010, 33(6): 1732-1742. DOI:10.2514/1.49978 |
| [8] | TETSUJIRO Ninomiya, YOSHIKAZU Miyazawa. Neural network based adaptive control with hierarchy structured dynamic inversion applied to nonlinear aircraft model[C]//AIAA Guidance, Navigation, and Control Conference, 2010 |
| [9] | LAKSHMIKANTH G S, PADHI R, WATKINS J M, et al. Adaptive flight-control design using neural-network-aided optimal nonlinear dynamic inversion[J]. Journal of Aerospace Information Systems, 2014, 11(11): 785-806. DOI:10.2514/1.I010165 |
| [10] | CAO C, HOVAKIMYAN N. Design and analysis of a novel L1 adaptive controller, part I: control signal and asymptotic stability[C]//American Control Conference, 2006 |
| [11] | LI Z, HOVAKIMYAN N. L1 adaptive controller for MIMO systems with unmatched uncertainties using modified piecewise constant adaptation law[C]//IEEE Conference on Decision & Control, 2012: 7303-7308 |
| [12] |
周艳, 刘慧英, 李靖. 带执行器故障的L1自适应飞行器横侧向容错控制[J]. 西北工业大学学报, 2019, 37(5): 937-942.
ZHOU Yan, LIU Huiying, LI Jing. L1 adaptive for aircraft lateral fault tolerant control with actuator failure[J]. Journal of Northwestern Polytechnical University, 2019, 37(5): 937-942. (in Chinese) |
| [13] |
高丽, 吴文海, 梅丹, 等. 侧向自动着舰引导控制L1自适应设计[J]. 飞行力学, 2016(4): 41-45.
GAO Li, WU Wenhai, MEI Dan, et al. Design of L1 adaptive controller for lateral-directional automatic carrier landing[J]. Flight Dynamics, 2016(4): 41-45. (in Chinese) |
| [14] |
李煜, 刘小雄, 李吉宽, 等. 基于L1自适应着舰纵向控制与特性分析[J]. 计算机测量与控制, 2018, 26(12): 120-124.
LI Yu, LIU Xiaoxiong, LI Jikuan, et al. Design the characteristic analysis of L1 adaptive longitudinal control for carrier-based landing[J]. Computer Measurement & Control, 2018, 26(12): 120-124. (in Chinese) |
| [15] | POMET J B, PRALY L. Adaptive nonlinear regulation: estimation from the Lyapunov equation[J]. IEEE Trans on Automatic Control, 1992, 37(6): 729-740. DOI:10.1109/9.256328 |
| [16] | NGUYEN L T, OGBURN M E, GILBERT W P, et al. Simulator study of a stall/post-stall characteristics of a fighter airplane with relaxed longitudinal static stability[R]. TP1538, NASA, Hampton, VA, 1979 |
2. Shaanxi Province Key Laboratory of Flight Control and Simulation Technology, Xi'an 710129, China;
3. AVIC Chengdu Aircraft Design and Research Institute, Chengdu 610091, China




