2. 液体火箭发动机技术国防科技重点实验室, 陕西 西安 710100
有限单元法(FEM)是一种通过将无限自由度问题离散为有限自由度,从而得到近似结果的高效数值算法,该方法自问世以来就在很多领域内得到了广泛应用。目前对于三维有限元问题,四面体和六面体单元具有原理简单、网格生成算法成熟等优点,被绝大多数商业软件所采用。然而在面对大型复杂结构时,四面体网格计算精度差,六面体网格难以划分等缺点也逐渐突出。
近年来,多面体单元由于其单元面的形状和数量都具有任意性,为网格生成提供了巨大的灵活性等特点而受到广泛关注[1-9]。然而因为难以构造满足单元协调性的多项式形式的形函数以及网格生成算法不够成熟,与常规有限元相比其发展仍然处于起步阶段。
刘桂荣教授和Nguyen-Thoi创立了一系列的光滑有限元法(S-FEM)[10],由最初的光滑子单元域有限元法(CS-FEM)[11],之后推广到光滑节点域有限元法(NS-FEM)[12]、光滑面域有限元法(FS-FEM)[13]和光滑边域有限元法(ES-FEM)[14]。这些方法都具有一个共同的特点,即不需要对形函数求导,降低了形函数必须连续的要求,这一特点可以有效地解决使用多面体网格遇到的问题。
在以上这些S-FEM算法中,二维光滑边域有限元法被证明具有最佳的稳定性和精度[14]。所以本文在二维ES-FEM基础上,建立了基于多面体单元的三维光滑边域有限元法,划分了三维ES-FEM在多面体单元中的的光滑域,推导了几何矩阵和刚度矩阵。通过Matlab软件编制的计算程序计算了弹性力学典型三维算例,并将结果与常规有限元结果等进行了对比研究,证实了基于多面体单元的三维ES-FEM方法的可行性与可靠性。
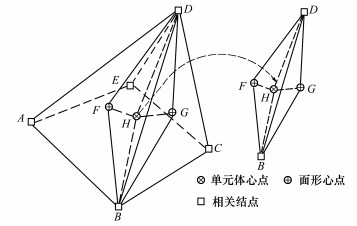
1 ES-FEM-Poly的基本理论在多面体网格中, ES-FEM-Poly以多面体单元的边为基准, 在与该边相邻的n个单元中划分n个光滑子域, n个光滑子域组成了一个以该边为基准的光滑域。本文研究的多面体为包括四面体, 六面体在内的任意面体。图 1给出了以五面体单元为例的光滑子域的划分方法, 光滑子域由基准边的2个端点B、D, 邻接单元面的形心F、G, 邻接单元的体心H组成的五结点六面体。在多面体网格中, 一个边的邻接单元数量不定, 所以组成一个光滑域的光滑子域数量也不定, 模型中边的数量等于光滑域数量。
|
| 图 1 五面体单元光滑子域划分方法 |
与常规有限元方法相同, 首先将模型离散为有限个单元, 然后按照上述方法划分出N个光滑域Ωks (k=1, 2, …, N), 再用基准边邻接单元的结点即相关结点的位移来表征光滑域的位移场
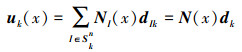
|
(1) |
式中:Skn为光滑域相关结点集合;N(x)为形函数矩阵;dk为相关结点位移向量。
ES-FEM-Poly的形函数并不是关于相关结点位移的连续函数, 不需要导数, 针对这一特点使用线性插值法[15], 直接计算相关结点在积分面上高斯积分点处的形函数值, 将高斯积分点取为每个面的形心。以图 1所示的五面体为例, 表 1给出了对应的形函数值表。表中第i行第j列的值代表第i个结点在第j个相关结点处的形函数值。
| 相关结点A | 相关结点B | 相关结点C | 相关结点D | 相关结点E | 点属性 | |
| A | 1 | 0 | 0 | 0 | 0 | 相关结点 |
| B | 0 | 1 | 0 | 0 | 0 | 相关结点 |
| C | 0 | 0 | 1 | 0 | 0 | 相关结点 |
| D | 0 | 0 | 0 | 1 | 0 | 相关结点 |
| E | 0 | 0 | 0 | 0 | 1 | 相关结点 |
| F | 1/3 | 1/3 | 0 | 1/3 | 0 | 相邻面形心 |
| G | 0 | 1/3 | 1/3 | 1/3 | 0 | 相邻面形心 |
| H | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 | 单元体心 |
| 1 | 8/45 | 8/45 | 1/15 | 23/45 | 1/15 | 高斯点1(HDF形心) |
| 2 | 1/15 | 8/45 | 8/45 | 23/45 | 1/15 | 高斯点2(HGD形心) |
| 3 | 1/15 | 23/45 | 8/45 | 8/45 | 1/15 | 高斯点3(HBG形心) |
| 4 | 8/45 | 23/45 | 1/15 | 8/45 | 1/15 | 高斯点4(HFB形心) |
| 5 | 1/9 | 4/9 | 0 | 4/9 | 0 | 高斯点5(DBF形心) |
| 6 | 0 | 4/9 | 1/9 | 4/9 | 0 | 高斯点6(BDG形心) |
对于一个拥有n个结点的多面体单元, 每个结点在体心处的形函数值是1/n, 在其他位置计算形函数的方法与五面体单元相同。
利用应变光滑技术, 将光滑域内的应变场变为常量, 用εk(x)表示
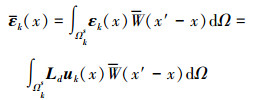
|
(2) |
式中: Ld为微分算子矩阵; εk(x)为光滑域相容应变场; W(x′-x)为权函数, 定义为
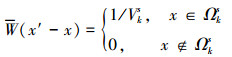
|
(3) |
式中, Vks为光滑域体积。将(3)式代入(2)式, 根据高斯定理, 将体积分转换为面积分, 得到光滑域应变
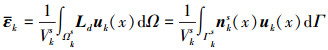
|
(4) |
式中:Γks为围成光滑域的所有面的集合;nks(x)为光滑域面的单位外法线向量矩阵, 可以看到光滑应变的求解无需求导。
将(1)式代入(4)式中, 可得
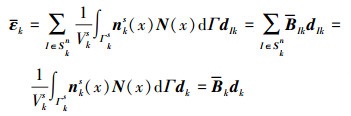
|
(5) |
式中,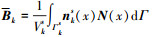
ES-FEM-Poly的总体平衡方程可由光滑Garlerkin弱化形式[13]得到
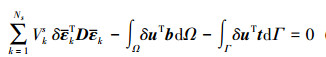
|
(6) |
式中:b为体积力向量;t为边界牵引力向量;D为弹性系数矩阵。
将(1)式和(5)式代入(6)式并简化可得

|
(7) |
式中:为光滑域刚度矩阵, 其表达式为
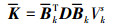
|
(8) |
接下来, 将每个光滑域的刚度矩阵按照常规有限元方法组装成整体刚度矩阵, 然后求解平衡方程。
从以上推导过程可以看出, ES-FEM-Poly对光滑域的边界进行积分而无需对光滑域积分, 从而无需像常规有限元那样对坐标进行映射, 它只要求多面体单元任意边的2个结点与单元形心所组成的三角形面必须位于单元内部, 因此大大降低了对网格质量的要求, 即使是单元内两相邻面内角大于180°的畸形网格也同样能满足要求。
2 算例分析本文利用Matlab软件编写了ES-FEM-Poly算法程序, 计算了空心球模型和悬臂梁模型, 将计算结果与常规有限元四面体单元(FEM-T4)和六面体单元(FEM-H6)所得结果通过应力相对误差和能量相对误差进行比较。
应力相对误差

|
(9) |
式中, 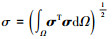
能量相对误差
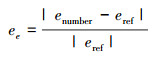
|
(10) |
式中:
由于本文所用网格类型不同, 且形状不规则, 引入单元特征边长来表征网格疏密程度。

|
(11) |
式中:VΩ, Ne分别为整个模型的体积和单元个数。
2.1 空心球模型空心球内外半径分别为a=5 m, b=10 m, 弹性模量E=72 GPa, 泊松比μ=0.33, 因其对称性, 仿真计算时只取1/8模型, 在其内表面施加P=100 MPa的压力, 在其3个对称面上分别施加x, y, z方向的位移约束, 如图 2所示。
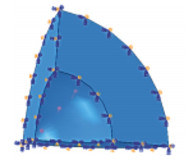
|
| 图 2 1/8空心球模型示意图 |
|
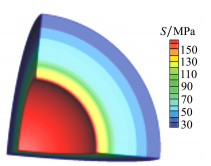
| 图 3 球模型参考应力云图 |
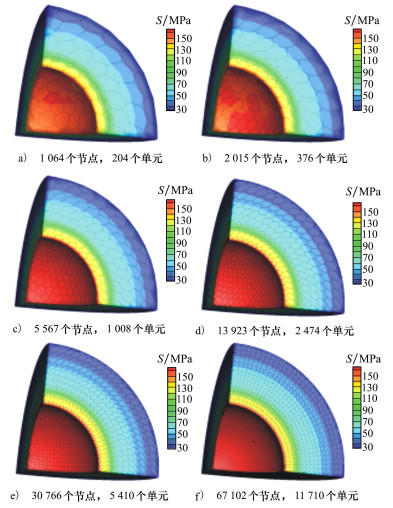
选取1 016 379个六面体单元网格计算所得结果为参考解, 图 3给出了参考应力云图, 图 4给出了不同数量多面体单元对应的应力云图。从图中可以看出, 应力分布随着单元数量的增加越来越接近参考解的应力分布。
|
| 图 4 不同数量多面体单元的应力云图 |
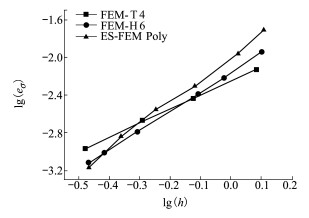
图 5给出了不同数值方法下应力相对误差随单边特征边长的收敛曲线。从图中可以看出, 3条曲线比较接近, 表明不同方法应力误差相差不大, 但ES-FEM-Poly曲线的斜率明显大于FEM-H6和FEM-T4的曲线斜率, 表明:随单元数量增加, lg(h)减小, ES-FEM-Poly计算结果更趋近参考解, 表明其有更好的收敛性。当h < 0.5 m,即lg(h) < -0.3时, ES-FEM-Poly的精度高于FEM-T4;当h < 0.38 m,即lg(h) < -0.42时, ES-FEM-Poly的精度高于FEM-H6。
|
| 图 5 各算法的应力相对误差收敛曲线 |
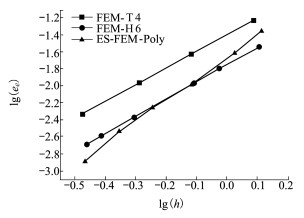
图 6给出了不同数值方法下能量相对误差随单边特征边长的收敛曲线。从图中可以看出, ES-FEM-Poly和FEM-H6的精度相似, 且高于FEM-T4;但ES-FEM-Poly曲线的斜率大于FEM-H6和FEM-T4的曲线斜率, 表明ES-FEM-Poly的收敛性要比FEM-H6和FEM-T4好。
|
| 图 6 各算法的能量相对误差收敛曲线 |
如图 7所示, 长和宽为5 m, 高为60 m的三维悬臂梁模型一端固支, 另一端受到方向沿Y轴负方向的10 MPa均布剪力。弹性模量E=72 GPa, 泊松比μ=0.33。
|
| 图 7 梁模型示意图 |
选取2 976 750个六面体单元网格计算所得结果为参考解, 图 8给出了参考应力云图, 图 9给出了不同数量多面体单元对应的应力云图。从图中可以看出, 应力分布随着单元数量的增加越来越接近参考解的应力分布。

|
| 图 8 梁模型参考应力云图 |

|
| 图 9 不同数量多面体单元的应力云图 |
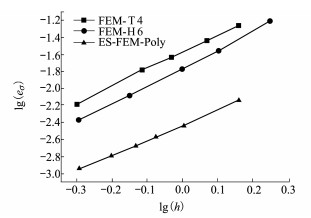
图 10给出了梁模型应力相对误差随单边特征边长的收敛曲线。从图中可以看出, ES-FEM-Poly的曲线明显低于FEM-T4和FEM-H6, 表明ES-FEM-Poly的计算精度显著高于FEM-T4和FEM-H6。当h=0.5 m,即lg(h)=-0.3时, ES-FEM-Poly的应力相对误差是FEM-H6的1/4, 是FEM-T4的1/6。
|
| 图 10 各算法的应力相对误差收敛曲线 |
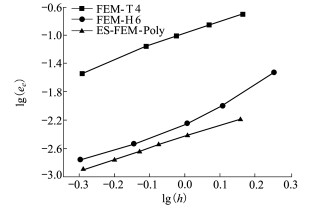
图 11给出了梁模型能量相对误差随单边特征边长的收敛曲线。从图中可以看出, 使用多面体单元的ES-FEM-Poly的计算精度与FEM-H6相近, 但显著高于FEM-T4。当h=0.5 m,即lg(h)=-0.3时, ES-FEM-Poly的能量相对误差是FEM-T4的1/24。
|
| 图 11 各算法的能量相对误差收敛曲线 |
本文建立了基于多面体网格的光滑边域有限元法, 介绍了多面体单元的光滑域划分方法、形函数的构造以及几何矩阵和刚度矩阵的推导, 利用Matlab软件编程计算了空心球模型和梁模型, 并将结果与常规有限元结果进行对比研究, 可以看出:①ES-FEM-Poly曲线的斜率明显大于FEM-H6和FEM-T4的曲线斜率, 表明随着单元数量增加, ES-FEM-Poly计算结果更趋近参考解, 有更好的收敛性;②ES-FEM-Poly曲线明显低于FEM-H6和FEM-T4曲线, 表明在单元特征边长一定时, ES-FEM-Poly计算结果更接近参考解, 精度更高。
综上所述,基于多面体网格的三维光滑边域有限元法, 相比于常规有限元方法具有更好的精度和收敛性, 可以用该方法对结构复杂的三维弹性力学问题进行分析。
| [1] | HUO S H, LIU G R, ZHANG J Q, et al. A smoothed finite element method for octree-based polyhedral meshes with large number of hanging nodes and irregular elements[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 359: 112646. DOI:10.1016/j.cma.2019.112646 |
| [2] | LEE Chan, KIM Hobeom, IM Seyoung. Polyhedral elements by means of node/edge-based smoothed finite element method[J]. International Journal for Numerical Methods in Engineering, 2017, 110(11): 1069-1100. DOI:10.1002/nme.5449 |
| [3] | AMRITA F, BERNARDIN A O, STÉPHANE A B, et al. Linear smoothed polygonal and polyhedral finite elements[J]. International Journal for Numerical Methods in Engineering, 2017, 109(9): 1263-1288. DOI:10.1002/nme.5324 |
| [4] | ZHANG Junqi, Natarajan Sundararajan, OOI Ean Tat, et al. Adaptive analysis using scaled boundary finite element method in 3D[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 372: 113374. DOI:10.1016/j.cma.2020.113374 |
| [5] | BEIRÃO da L Veiga, DASSI F, RUSSO A. High-order virtual element method on polyhedral meshes[J]. Computers and Mathematics with Applications, 2017, 74(5): 1110-1122. DOI:10.1016/j.camwa.2017.03.021 |
| [6] | SON Nguyenhoang, DONG Woosohn, KIM Hyungyu. A new polyhedral element for the analysis of hexahedral-dominant finite element models and its application to nonlinear solid mechanics problems[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 324: 248-277. DOI:10.1016/j.cma.2017.06.014 |
| [7] | SUNDARARAJAN Natarajan, STEPHANE PA Bordas, EAN Tat Ooi. Virtual and smoothed finite elements: a connection and its application to polygonal/polyhedral finite element methods[J]. International Journal for Numerical Methods in Engineering, 2015, 104(13): 1173-1199. DOI:10.1002/nme.4965 |
| [8] |
盛国雨. 基于径向积分法的多边形及多面体有限元方法[D]. 大连: 大连理工大学, 2015 SHENG Guoyu. Polygonal and polyhedral finite element method based on radial integration method[D]. Dalian: Dalian University of Technology, 2015(in Chinese) |
| [9] |
程尧舜, 李刚. 任意凸多面体间断有限单元法[J]. 结构工程师, 2007(2): 43-47.
CHENG Yaoshun, LI Gang. A discontinuous convex polyhedral finite element method[J]. Structural Engineers, 2007(2): 43-47. (in Chinese) DOI:10.3969/j.issn.1005-0159.2007.02.010 |
| [10] | LIU G R, NGUYEN-THOI T. Smoothed finite element methods[M]. New York: CRC Press, Taylor and Francis Group, 2010. |
| [11] | LIU G R, DAI K Y, Nguyen T A. A smoothed finite element method for mechanics problems[J]. Computational Mechanics, 2007, 39(6): 859-877. DOI:10.1007/s00466-006-0075-4 |
| [12] | NGUYEN-THOI T, VU-DO H C, RBACZUK T, et al. A node-based smoothed finite element method(NS-FEM) for upper bound solution to visco-elastoplastic analyses of solids using triangular and tetrahedral meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(45): 3005-3027. |
| [13] | NGUYEN-THOI T, LIU G R, VU-DO H C, et al. A face-based smoothed finite element method (FS-FEM) for visco-elastoplastic analyses of 3D solids using tetrahedral mesh[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(41): 3479-3498. |
| [14] | LIU G R, NGUYEN-THOI T, LAM K Y. An edge-based smoothed finite element method(ES-FEM) for static, free and forced vibration analyses of solids[J]. Journal of Sound and Vibration, 2008, 320(4): 1100-1130. |
| [15] | DAI K Y, LIU G R, NGUYEN T T. An n-sided polygonal smoothed finite element method(n SFEM) for solid mechanics[J]. Finite Elements in Analysis & Design, 2007, 43(11): 847-860. |
2. National Key Laboratory of Science and Technology on Liquid Rocket Engine, Xi'an 710100, China




