直升机在前飞过程中,旋翼前行侧和后行侧的相对气流速度不同,拉力分布不均匀,由此引起的周期性运动容易导致后行桨叶由于迎角过大产生气流分离而失速[1]。在大速度前飞时,旋翼后行侧的失速不仅限制了直升机飞行速度提高,而且失速过程中桨叶上表面的涡不断生成和耗散脱落,会引发升力突降等问题,严重危害直升机飞行安全。因此,提升直升机前飞时的旋翼气动特性已成为直升机气动领域的研究热点。
国内外针对直升机旋翼动态失速及提升前飞性能的研究由来已久。对于二维翼型,Sahin等[2]通过数值计算发现,使用变前缘外形的方法可以有效抑制低马赫数下二维翼型动态失速涡的发展,从而有效提升气动特性。对于前缘弹性下垂变形的研究,Bain等[3]使用了2种网格变形方法,表明动态前缘下垂(variable droop leading edge, VDLE)可以有效维持翼型表面气流的附着状态。Chandrasekhara[4]针对VDLE导致的升力系数整体偏低的现象,提出采用格尼襟翼来提升整体的升力。对于提升三维旋翼前飞性能的研究,Johnson等[5]对前飞旋翼的不同桨叶外形进行了优化设计,旨在约束升阻比以及阻力发散的条件下,提高升力系数,减小阻力系数。经过对比发现,经过优化后的桨叶表面分布的升力系数有所提高,桨尖涡明显缩小且更加集中。Geissler等[6]对全尺寸桨叶的前缘10%c下垂进行了试验和数值计算研究,结果表明使用VDLE可以有效提升升力系数,对气动特性有明显改善。此外,协同射流[7-8]、合成射流[9-11]、涡流发生器[12]、改变桨叶气动外形[13]等方法也被用于主动流动控制以及提升直升机旋翼气动特性等研究。目前使用动态前缘下垂进行流动控制的研究大部分针对二维翼型,对使用VDLE提升三维旋翼气动特性的研究仍较为欠缺。
综上所述,本文针对后行侧桨叶采用动态前缘下垂方法,开展了不同前缘下垂幅值对提升中等前进比的三维旋翼前飞气动特性性能的研究。使用雷诺平均N-S方程,运用运动嵌套网格及基于径向基函数(radial basis function, RBF)[13]的网格变形技术,对不同角度的动态前缘下垂开展旋翼的气动参数及桨叶表面涡结构的发展的参数化研究。
1 数值模拟方法 1.1 流场控制方程为了捕捉非定常流场的涡流动特性,本文采用可压缩的navier-stokes(N-S)方程作为流场求解的控制方程,建立如下N-S方程。
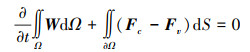
|
(1) |
式中:W为守恒变量;Ω和S分别为控制体体积和表面;Fc, Fv分别为对流通量和黏性通量。空间离散采用Roe通量差分分裂格式, 时间推进采用隐式[15]方法, 湍流模型使用SST-kω。本文在数值模拟过程中不考虑旋翼轴前倾, 设定旋翼升力系数CL、扭矩系数CQ、等效升阻比CL/De以及剖面法向力系数Cn分别如下
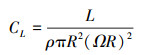
|
(2) |
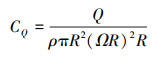
|
(3) |
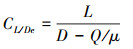
|
(4) |

|
(5) |
式中: L, Q, D分别为旋翼升力、扭矩以及水平方向阻力; μ为前进比; FN为桨叶剖面的法向力; a为声速; c为弦长。
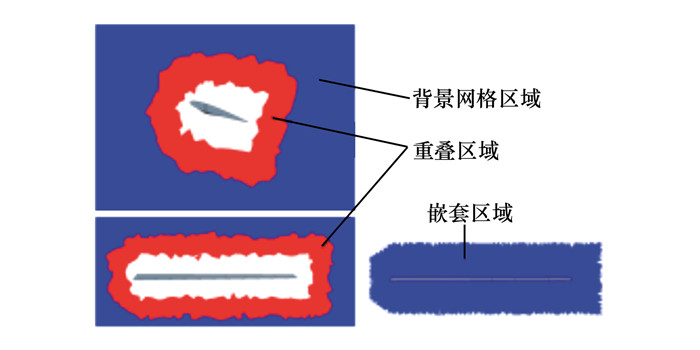
1.2 运动嵌套网格及网格变形技术本文使用的运动嵌套网格系统包含背景网格和围绕旋翼的贴体网格。该方法在桨叶网格区域与背景网格的重叠交界面处通过洞单元识别、贡献单元搜索等, 对背景网格的相应区域进行挖洞, 如图 1所示。
|
| 图 1 运动嵌套网格示意图 |
在桨叶网格绕旋翼轴旋转运动过程中, 重叠区域随着桨叶网格的运动不断更新。为实现桨叶网格区域与背景网格的信息传递, 本文通过距离加权法对邻近网格单元进行插值。
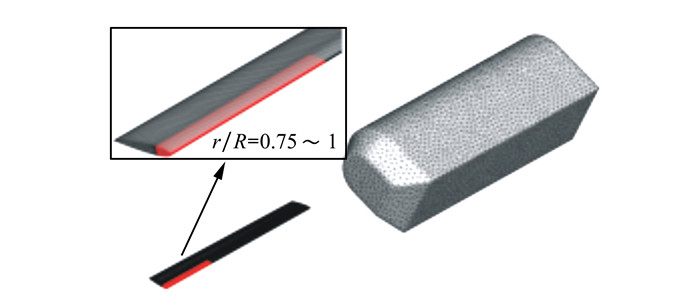
设定动态前缘的运动规律为δ=δ0+δmsin· (2k*kt), δ为翼型前缘瞬时下垂角, δ0和δm分别为基准状态下前缘的下垂角和偏转幅值, k为翼型振荡减缩频率, k*为相对于k的无量纲频率。本文研究的前缘下垂范围, 主要针对桨叶展向0.75R~R, 弦向位置为前缘25%c部分, 如图 2所示。为避免由于前缘下垂而导致桨叶表面在过渡部分出现折角等突变, 本文在VDLE与基准桨叶的连接处, 设置2%c的区域作为网格变形的过渡部分。
|
| 图 2 桨叶前缘下垂范围示意图 |
本文采用网格变形方法来实现指定前缘的动态下垂运动。变形使用控制点位移为区域生成一个插值场, 然后使用该插值场将网格节点平移到新位置。变形算法根据边界位移重新分布网格节点, 使网格可以进行非刚性变形。网格变形使用RBF插值方法, 使用控制点及其指定的位移创建方程, 其中每个控制节点i的已知位移d′i展开为如下方程
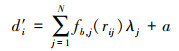
|
(6) |
式中:fb, j(rij)是形状的径向基本函数;rij为2个节点之间的距离幅值;λj为展开系数;N为控制节点的数量;a为常数矢量。
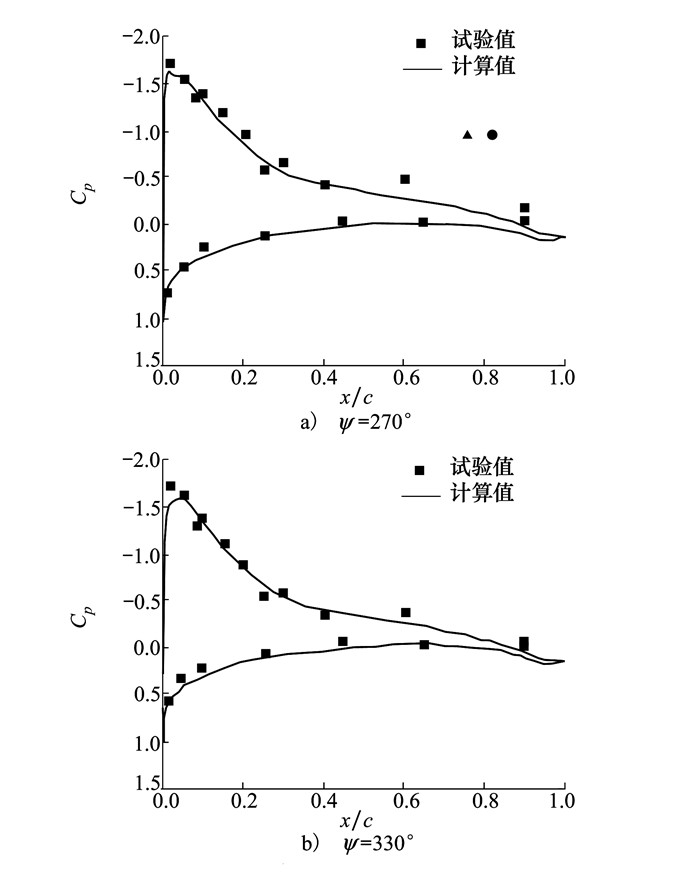
1.3 算例验证为验证本文计算方法的有效性, 首先对已有试验数据的SA349/2旋翼的前飞状态进行算例验证。该旋翼采用3片矩形桨叶。OA209翼型、线性负扭转。旋翼半径R=5.25 m, 弦长0.35 m, 桨尖马赫数为0.626, 前进比为0.26时, 旋翼周期变距为θ=8.42°-2.14°sinψ+1.25°cosψ。计算得到r/R=0.97剖面在不同方位角处的Cp与试验值[16]的对比如图 3所示。从图中可以看出, 本文计算得到的旋翼表面Cp值与试验值均吻合良好。表明本文建立的计算方法能够有效进行三维旋翼前飞状态的模拟。
|
| 图 3 r/R=0.97处Cp验证结果图 |
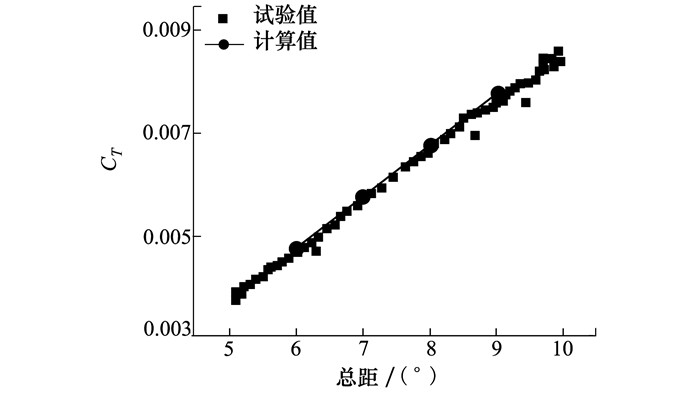
图 4进一步给出了7A旋翼悬停状态Mtip=0.617时的拉力系数与试验值[17]的对比。该旋翼采用4片矩形桨叶, 由OA209和OA213翼型分段配置而成, 具有分段线性负扭转。图中可见, 本文使用的计算方法能够对旋翼拉力系数进行较为精确的模拟。
|
| 图 4 7A旋翼拉力系数验证图 |
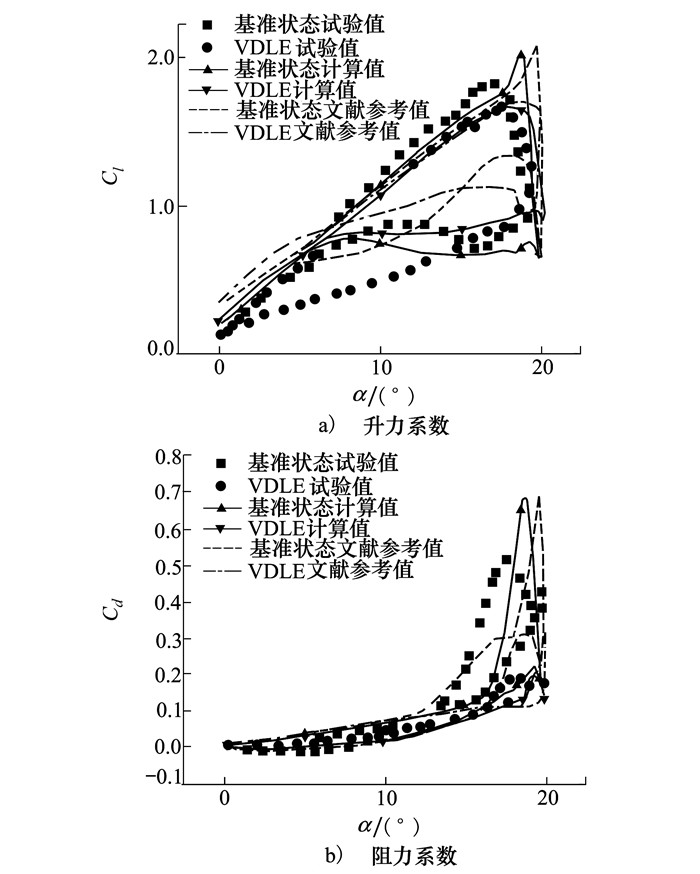
对于动态前缘下垂的算例验证, 本文选用已有试验数据的VR-12翼型, 来流Ma=0.4, 翼型振荡规律为α=10°+10°sin(2kt), k=0.1, 旋转中心为距前缘1/4c处, 动态前缘的偏转规律为δ=10°+10°sin(2k*kt), 其中k*=1。计算得到气动参数Cl, Cd与试验值、文献计算值[18]对比如图 5所示。图中可见, 本文的计算值相对文献计算参考值而言, 与试验值更为接近, 表明本文使用的网格变形方法可以有效模拟翼型前缘动态下垂的真实流场状态。
|
| 图 5 VR-12翼型气动参数验证图 |
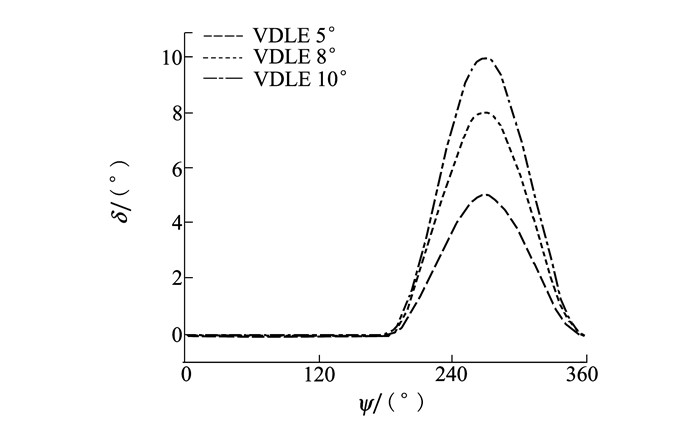
针对三维旋翼的研究, 为了综合考虑计算成本, 本文选用2片矩形桨叶, 翼型采用OA209, 旋翼半径R=2.1 m, 弦长c=0.2 m, 线性负扭转为-4.8°/m。计算状态:桨尖马赫数为0.647;前进比为0.3。经过配平得到相应的周期变距θ=12.5°-6.3°sinψ+1.1°cosψ。本文分别针对前缘下垂幅值δm为5°, 8°, 10°进行研究, k*均取2, 以防止由于较大的前缘下垂启停加速度而给桨叶带来振动等不利影响。当前缘下垂时, 该部分的相对迎角减小, 为避免迎角较小的前行侧桨叶由于前缘下垂而造成一定的升力损失, 本文仅对后行侧桨叶设置前缘下垂的运动。前缘下垂规律随方位角的变化如图 6所示。图 7给出了基准状态桨叶与前缘下垂角为10°时桨叶前缘的对比图。使用RBF网格变形方法使前缘下垂10°后, 桨叶表面网格仍排列有序, 接缝处没有出现较大的不平整, 与实际的桨叶前缘下垂情况较为符合。
|
| 图 6 动态前缘下垂规律 |

|
| 图 7 桨叶前缘下垂前后对比图 |
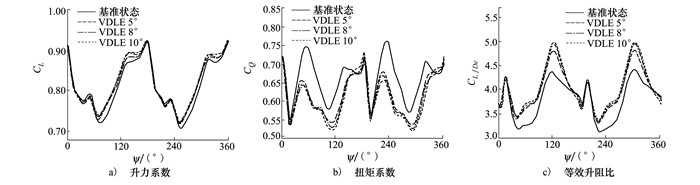
图 8给出了不同前缘下垂幅值下旋翼气动特性参数随方位角变化的对比图。使用VDLE后, 旋翼升力系数CL在不同方位角处均有一定提升。本文主要针对2片桨叶, 可见在240°~360°方位角之间, 使用VDLE可以有效提升旋翼升力, 在277°方位角时升力提升达5.5%。随着前缘下垂幅值增加, 升力仅在330°方位角附近有进一步提升。使用VDLE之后, 旋翼扭矩系数相对基准状态明显降低。随着下垂幅值的增加, 扭矩系数仍有一定的降低, 在Ψ=240°附近的CQ降幅相比于基准状态最大可达18%, 但在180°方位角附近, δm=10°时旋翼扭矩反而超过基准状态。结合图 6分析可知, 这是由于δm=10°时, 前缘下垂的角加速度最大, 相同方位角下瞬时δ也最大。而180°方位角附近的桨叶迎角较小, 此时一定的前缘下垂反而容易引起阻力增加。从等效升阻比可以看出, 使用VDLE后, 后行侧桨叶的等效升阻比得到了明显提升, 这是旋翼升力增加和扭矩显著降低综合作用的结果。与基准状态相比, CL/De在250°方位角附近提升约15.5%, 但随着VDLE的下垂幅值δm的增加, 等效升阻比并没有持续显著增加, δm为8°和10°时的等效升阻比区别并不明显。
|
| 图 8 旋翼气动特性对比图 |
使用Q准则计算得到的桨尖附近瞬时速度等值涡量图如图 9所示。图中可见, 基准状态的桨叶除了离散的桨尖涡外, 桨叶上表面还附着有较多的涡。随着方位角从270°增加到300°, 涡的体积增大并逐渐从上表面分离和耗散。当前缘下垂后, 虽然270°方位角时桨叶上表面在0.8R内侧仍存在分离涡, 但0.8R~R处桨叶上表面涡的数量显著减少。在300°方位角时, 0.8R以内的涡在展向流的作用下向桨尖方向偏移, 使0.8R剖面的后缘附近出现较为明显的分离涡。随着前缘下垂角的增大, 桨叶表面的涡体积及数量略有减少, 但差异并不明显, 这与图 8中气动参数的结论一致。相对于基准状态, 前缘下垂后0.9R附近没有出现较大的分离涡, 表明桨尖附近前缘下垂能够有效抑制桨尖上表面附近分离涡的生成, 对改善后行侧桨叶的流场状态有明显效果。

|
| 图 9 不同前缘下垂角的桨尖附近等值涡量图 |
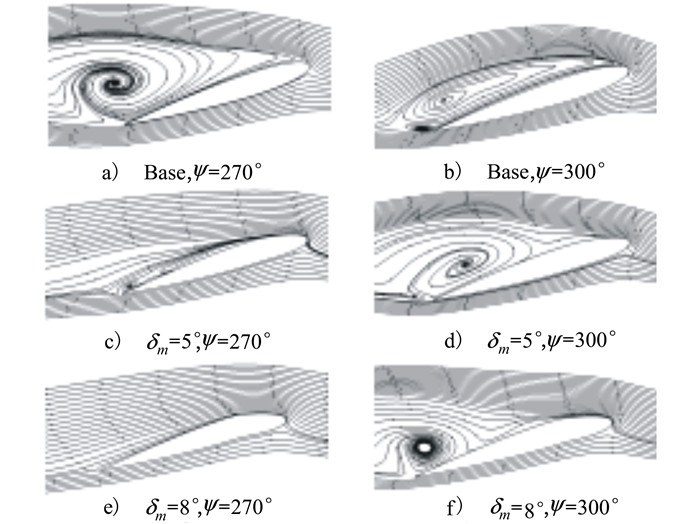
为了更加直观地描述桨叶上表面涡的分布及发展过程, 图 10给出了0.8R剖面处不同方位角的流线图。结合图 9可知, Ψ=270°时, 基准状态下该剖面气流从前缘附近即开始分离, 上表面几乎完全处于气流分离状态, 而后该涡耗散脱落, 在Ψ=300°时生成新的涡结构, 该涡结构同样是从该剖面前缘分离而来。当VDLE下垂幅值δm=5°时, 该剖面尾缘处均存在失速涡。Ψ=300°时较大的失速涡为0.8R内侧的前缘分离涡向下游衍生发展而来。从Ψ=300°时位于后缘附近的尺寸明显减小的涡可以看出, VDLE幅值δm=10°对0.8R内侧的失速涡有更好的控制效果, 综合表明一定的前缘下垂可以有效抑制桨尖附近前缘分离涡的生成。
|
| 图 10 r/R=0.8处截面的速度流线图 |
桨叶0.8R与0.9R剖面的法向力系数Cn在后行侧的分布如图 11所示。在0.8R处使用VDLE后, Cn的最低点从270°方位角附近延迟到285°附近, 其系数波动的方位角跨度有所减小。较小的下垂幅值如δm=5°即可明显缩小Cn波动的横向方位角跨度。当δm=10°, 其在270°~330°方位角之间的纵向振荡幅度有效减小66.3%。虽然使用VDLE后, 该剖面处仍有因气流分离而引起的系数Cn波动, 但波动的幅值和跨度均有明显减小。VDLE在0.9R剖面的改善效果更为明显, Cn在后行侧振荡的横向跨度随Ψ=280°附近的第一波谷的消失而缩小近30°。随着δm的增大, Cn系数整体提升, Ψ=280°附近δm=5°, 8°时的Cn分别提升22.7%以及44.8%。但δm为8°和10°时的区别并不明显。结合上文分析可知, 这是由于前缘下垂后, 该剖面前缘附近并没有发生气流分离, 其扰动主要来源于桨叶0.8R剖面内侧的前缘分离涡随展向流向下游发展而来, 因此影响并不明显。

|
| 图 11 截面法向力系数对比图 |
本文结合运动嵌套网格方法和基于RBF的网格变形技术, 将动态前缘下垂方法应用于三维前飞旋翼后行侧的流动控制中。针对μ=0.3的前飞状态, 开展了动态前缘下垂幅值对旋翼气动特性的参数化研究。通过对旋翼气动特性、桨尖附近等值涡量图、桨叶剖面流线图等分析, 得到以下结论:
1) 动态前缘下垂可以有效提升旋翼的升力系数, 减小扭矩系数, 使得旋翼等效升阻比最大可增加15.5%, 从而有效提升旋翼的气动特性。在一定范围内, 随着前缘下垂幅值δm的增加, 气动特性进一步提升。
2) 基准状态下, 后行桨叶上表面会出现分离涡, 严重影响旋翼的气动特性。当桨尖附近前缘下垂后, 0.8R剖面到桨尖附近的失速涡数量和尺寸明显减少, 流场状态有明显改善。
3) 动态前缘下垂可以有效减小后行桨叶桨尖附近剖面法向力系数的横向振荡跨度和振荡幅值, 表明该剖面处的涡数量和强度有所减小。此外, 一定范围内, 随着前缘下垂幅值的增加, 靠近桨尖附近的剖面(r/R=0.9)法向力系数整体有所提升, 表明使用VDLE后桨尖附近气动特性提升明显。
| [1] | LEISHMAN G J. Principles of helicopter aerodynamics with CD extra[M]. Cambridge: Cambridge University Press, 2006. |
| [2] | SAHIN M, SANKAR L N, CHANDRASEKHARA M S, et al. Dynamic stall alleviation using a deformable leading edge concept-a numerical study[J]. Journal of Aircraft, 2003, 40(1): 77-85. DOI:10.2514/2.3060 |
| [3] | BAIN J J, SANKAR L N, PRASAD J V R, et al. Computational modeling of variable-droop leading edge in forward flight[J]. Journal of Aircraft, 2009, 46(2): 617-626. DOI:10.2514/1.39174 |
| [4] | CHANDRASEKHARA M S. Optimum gurney flap height determination for "lost-lift" recovery in compressible dynamic stall control[J]. Aerospace Science and Technology, 2010, 14(8): 551-556. DOI:10.1016/j.ast.2010.04.010 |
| [5] | JOHNSON C, BARAKOS G. Optimising aspects of rotor blades in forward flight[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, 2011: 1194 |
| [6] | GEISSLER W, DIETZ G, MAI H, et al. Dynamic stall control investigations on a full size chord blade section[C]//30th European Rotorcraft Forum, Marseilles France, 2002 |
| [7] |
杨慧强, 许和勇, 叶正寅. 基于联合射流的翼型动态失速流动控制研究[J]. 航空工程进展, 2018(4): 16.
YANG Huiqiang, XU Heyong, YE Zhengyin. Study on the flow control of the dynamic stall using the co-flow jet[J]. Advances in Aeronautical Science and Engineering, 2018(4): 16. (in Chinese) |
| [8] |
许建华, 李凯, 宋文萍, 等. 低雷诺数下协同射流关键参数对翼型气动性能的影响[J]. 航空学报, 2018, 39(8): 88-102.
XU Jianhua, LI Kai, SONG Wenping, et al. influence of co-flow jet key parameters on airfoil aerodynamic performance at low Reynolds numbers[J]. Acta Aeroelastic et Astronautica Sinica, 2018, 39(8): 88-102. (in Chinese) |
| [9] | DURRANI N, HAIDER B A. Study of stall delay over a generic airfoil using synthetic jet actuator[C]//49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2011: 943 |
| [10] |
白俊强, 辛亮, 刘南, 等. 分布式零质量射流控制增升装置分离的数值模拟[J]. 西北工业大学学报, 2015, 32(2): 188-194.
BAI Junqiang, XIN Liang, LIU Nan, et al. Numerical simulation of separation control for high Lift system using distributed zero-net mass flux jet[J]. Journal of Northwestern Polytechnical University, 2015, 32(2): 188-194. (in Chinese) |
| [11] | ZHANG P F, YAN B, DAI C F. Lift enhancement method by synthetic jet circulation control[J]. Science China Technological Sciences, 2012, 55(9): 2585-2592. DOI:10.1007/s11431-012-4896-4 |
| [12] |
郝礼书, 乔志德, 宋文萍. 涡流发生器布局方式对翼型失速流动控制效果影响的实验研究[J]. 西北工业大学学报, 2011, 29(4): 524-528.
HAO Lishu, QIAO Zhide, SONG Wenping. Experimentally studying effects of different layouts of vortex generator on controlling stall flow over airfoil[J]. Journal of Northwestern Polytechnical University, 2011, 29(4): 524-528. (in Chinese) DOI:10.3969/j.issn.1000-2758.2011.04.005 |
| [13] | VU N A, LEE J W, SHU J I. Aerodynamic design optimization of helicopter rotor blades including airfoil shape for hover performance[J]. Chinese Journal of Aeronautics, 2013, 26(1): 1-8. DOI:10.1016/j.cja.2012.12.008 |
| [14] | GUMEROV N A, DURAISWAMI R. Fast radial basis function interpolation via preconditioned Krylov iteration[J]. SIAM Journal on Scientific Computing, 2007, 29(5): 1876-1899. DOI:10.1137/060662083 |
| [15] | STOLL P, GERLINGER P, BRVGGEMANN D, et al. Domain decomposition for an implicit LU-SGS scheme using overlapping grids[C]//13th Computational Fluid Dynamics Conference, 1997: 1896 |
| [16] | HEFFERNAN R M, GAUBERT M. Structural and aerodynamic loads and performance measurements of an SA349/2 helicopter with an advanced geometry rotor[R]. NASA TM-88370, 1986: 1-58 |
| [17] | POMIN H, WAGNER S. Navier-Stokes analysis of helicopter rotor aerodynamics in hover and forward flight[J]. Journal of Aircraft, 2002, 39(5): 813-821. DOI:10.2514/2.3001 |
| [18] | CHANDRASEKHARA M S, MARTIN P B, TUNG C. Compressible dynamic stall control using a variable droop leading edge airfoil[J]. Journal of Aircraft, 2004, 41(4): 862-869. DOI:10.2514/1.472 |




