矩量法[1]是一种精确的数值算法,广泛应用于分析天线、舰船、飞行器以及卫星的电磁性能。一般而言,对于未知数为N的问题,矩量法需要的存储量为O(N2),利用直接法和迭代法求解阻抗矩阵的计算复杂度分别为O(N3)和O(N2)。因此随着待求目标电尺寸的增加,其存储量和计算量将会迅速增长,导致求解效率降低,甚至无法求解。为了解决这个问题,近年来一些学者提出了许多基于矩量法的快速算法,如多层快速多极子[2](multilevel fast multipole algorithm, MLFMA),IE-FFT[3](integral equation fast fourier transformation)以及自适应积分法[4](adaptive integral method, AIM)等。在这些算法中,AIM基于等效近似源原理,不仅精度高并且不受目标形状限制。与矩量法相比,利用辅助基函数和格林函数的Toeplitz特性,AIM的内存需求量和计算复杂度分别为O(N1.5)和O(N1.5logN)。
许多改良算法的出现扩大了AIM的适用范围,如利用高阶基函数来提高AIM的精度[5-7],利用AIM分析分层媒质结构[8]、腔体结构[9]以及分区域AIM[10]来加快迭代求解效率等。然而在实际应用中,如计算导弹,舰艇,无人机等雷达散射截面(radar cross section, RCS),随着未知数越来越多,所有基于AIM的快速算法本质上都会存在2个难题:①近场矩阵填充耗时较长,虽然主因是电大尺寸目标近场元素较多,但是多次重复计算的双重三角积分加剧了这一影响;②迭代求解时间更长。由于电场积分方程属于第一类弗雷德霍姆方程,其特征值的谱聚特性较差,因此,使用迭代法求解这样的大型线性方程组时,常常会出现慢收敛和不收敛的情况。
针对上述2个问题,本文在保持精度不变的情况下,分别采用三角形循环策略和不完全LU(Incomplete LU, ILU)预处理来减少近场填充时间并加快迭代收敛速度。
1 算法原理 1.1 三角形循环策略以RWG[11]为基函数和检验函数填充阻抗矩阵时,一个阻抗元素需要计算4次二重三角积分,即
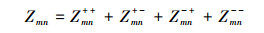
|
(1) |
式中,Zmn±±代表场源三角形Tm±和Tn±的相互作用。若采用边边循环的方式计算阻抗元素,当三角形个数为Nt,公共边N≈1.5Nt,填充整个阻抗矩阵需要计算4N2≈9Nt2次二重三角积分。很明显,每对三角形被重复计算了多次,这严重降低了填充阻抗矩阵的效率。
针对这一问题,文献[12]改变循环参量为三角形,先将双重积分的公共部分提取出来,然后再乘以相应的公共边系数,从而消除重复积分。以电场积分方程为例,考虑2个三角形P和Q,边m和n的部分互阻抗可以表示为
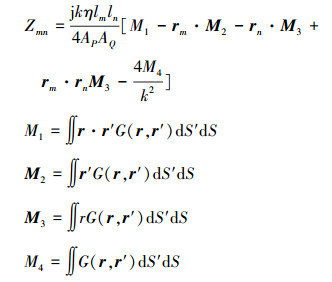
|
(2) |
式中,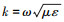
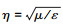
自适应积分法是一种基于矩量法的快速算法,它将满秩的阻抗矩阵根据近场门限dnear划分为近场和远场2个部分
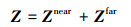
|
(3) |
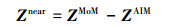
|
(4) |
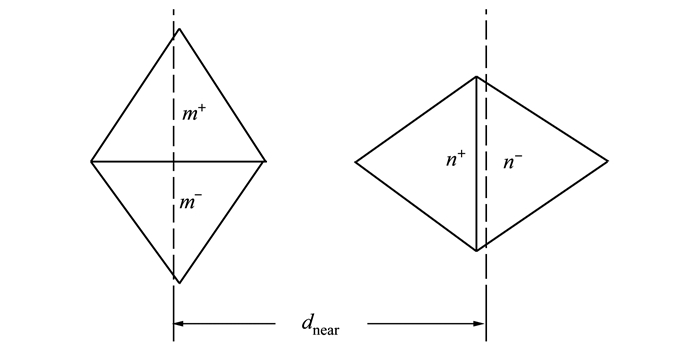
式中,Znear和Zfar分别表示近场稀疏矩阵和远场压缩矩阵,ZMoM表示准确的近场矩阵并使用边边循环方式填充,而ZAIM表示由离散格点产生的不准确近场矩阵。由于ZMoM并非完整的阻抗矩阵,只涉及部分三角形对,直接用三角形填充策略代替原有方式进行填充,无法确保(1)式中的4个积分项都被计算,从而导致错误的近场阻抗元素。如图 1所示,考虑位于近远区边界处的一对基函数fm和fn。根据它们公共边的距离,这对基函数所形成的阻抗元素Zmn属于近区。然而,如果直接将近场门限dnear用于区分三角形近远区的归属。则Zmn++和Zmn-+属于近区,会被计算,而Zmn--和Zmn+-则属于远区,不会被计算。结果,当循环完所有三角形后,由于缺失部分积分,阻抗元素Zmn的值显然是错误的。
|
| 图 1 位于近远区交界处的1对基函数fm,fn |
为了能够使用三角形循环策略加快ZMoM的填充速率,本节采用了一种双重间距检测方法来克服上述问题。该方法的原理是先根据三角形之间的距离,筛选出可能要计算积分的三角形对,其次再根据边边的距离,标记出要计算的边边组合,最后根据标记的组合数量分情况计算阻抗元素。由于不能使用近场门限dnear来划分三角形,因此本文引入三角形近场门限tnear>dnear。从图 1可以看出位于边界附近的三角形的间距略大于近场门限,其增加程度一般不会大于三角形边长。tnear的取值只需要稍大于dnear不宜取得过大,否则会增加第二次间距检测的计算量,经过数值实验,tnear取值范围应为1.2dnear~1.5dnear,本文中tnear取值为1.3dnear。
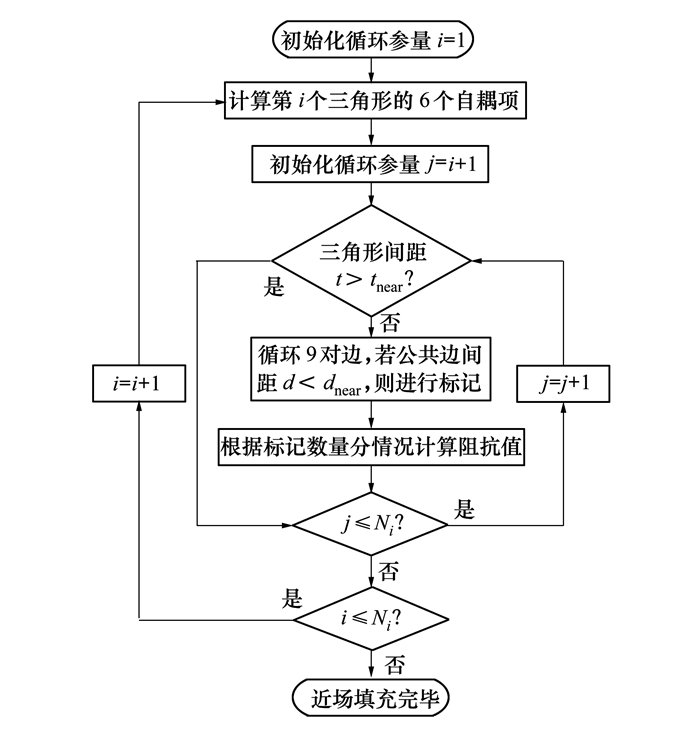
算法整体流程如图 2所示,在外层循环中先计算每个三角形的6个自耦项,然后进入内层循环,检测2个三角形的间距是否大于tnear。只有小于三角形近场门限的三角形对,会进行第二次距离检测,即判断2个三角形各3条边,共9种组合的间距,并标记间距d小于dnear的边边组合。最后根据标记的数量k来分情况计算被标记的阻抗元素:
|
| 图 2 近区阻抗矩阵ZMoM填充流程图 |
1) 当k=0时表示没有任何元素被标记,因此直接进行下一次循环;
2) 当k < 4时,由于(2)式至少要计算4次公共积分项,因此应该使用传统填充方式来计算k次积分;
3) 当k≥4时,使用(2)式来加速计算被标记的阻抗元素。
联合双重间距检测的三角形填充策略不仅简单而且高效。首先,它能够准确地定位所有属于近区的阻抗元素,确保计算的正确性。其次,它的计算量要远小于计算双重积分。最后,它采用先标记后计算的策略,根据标记的数量,使用不同的方法来最大限度地发挥了三角形循环策略的高效优势。
1.3 近场矫正与预处理采用三角形循环策略填充ZMoM时,完整的阻抗值必须等待循环完所有的近区三角形对才能得到,这表明矫正步骤必须从填充循环中分离。此时对于ZMoM中的每一个元素,可以用(5)式进行矫正
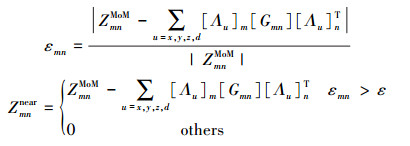
|
(5) |
式中:ε为给定的误差限;Λ为展开系数矩阵;G代表格林函数矩阵;ZmnMoM表示基函数fm和fn间正确的互阻抗。(5)式表明,当近似公式与传统矩量法计算的互阻抗大于给定的误差限ε时,才需要保存该阻抗元素的矫正值。因此,Znear的非零值要少于ZMoM,而近场矫正的计算量却并没有增加。
为了提高迭代求解时的收敛速度,通常会从阻抗矩阵Z中提取预处理矩阵M≈Z-1来改善矩阵病态特性。即原始方程组ZI=V变为
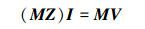
|
(6) |
式中,V代表右端激励项。但是在AIM中,阻抗矩阵被拆分为远近两部分,Zfar只在迭代时以矩阵相乘的形式隐式存在,Znear经过了矫正,无法提供正确的原始阻抗值。而临时的近场矩阵ZMoM则可以作为Z的近似替代用于提取预处理矩阵M≈[ZMoM]-1。
由于ZMoM为大型稀疏矩阵,为了保持稀疏特性,因此适合采用ILU来获得预处理矩阵M。本质上讲,在ILU中,稀疏矩阵L和U可以最大限度地近似ZMoM≈LU,其具体步骤可以参考文献[13], 本文采用Eigen3库中的ILU函数来实现矩阵预处理。此时,(6)式左边的矩阵与向量相乘可以表示为
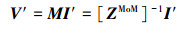
|
(7) |
式中
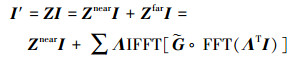
|
(8) |
式中,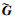
综上所述,算法的整体计算流程如下:
1) 读取RWG基函数数据,计算Λ和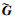
2) 利用1.2节的方法填充ZMoM;
3) 对ZMoM使用ILU分解,得到稀疏矩阵L和U;
4) 对ZMoM中的每一个元素使用(5)式来矫正,最终得到Znear;
5) 使用迭代法求解方程组(6),其中矩阵与向量相乘通过(7)式和(8)式来加速;
6) 计算散射体的散射场。
2 仿真与分析实验仿真平台为Intel Core i7 4790 3.6GHz PC机,选取金属球,圆锥,面包圈形和平板作为算例,计算其双站RCS来验证精度,通过与AIM对比近场计算时间和迭代收敛速度来验证本文方法的高效性。除非特殊说明,所有算例的激励为沿-z轴x方向线极化的平面波,AIM的近场门限dnear=0.3λ,三角形近场门限tnear=1.3dnear, 给定近场误差限为ε=0.01,迭代收敛条件为相对误差小于10-4,格点间距为0.05λ。
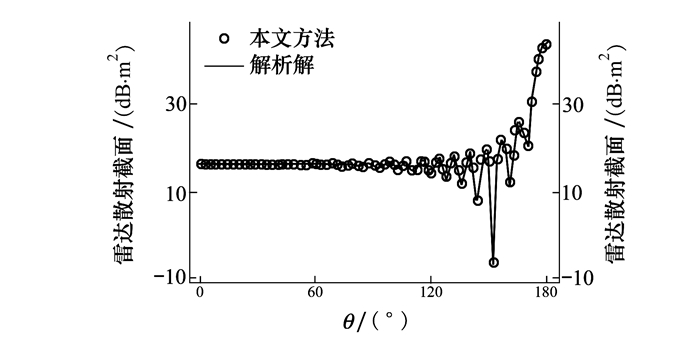
2.1 算法精度验证第一个算例是球心位于原点,半径r=3.6λ的金属球,用边长约为λ/12的三角形剖分球面,其未知量为97 353。图 3给出了利用本文方法得到的金属球俯仰面双站RCS,并与解析解进行对比。结果表明,本文的算法具有良好的精度。此外,对于这种电大尺寸的问题,如果采用传统矩量法,则需要消耗约141 GB内存,而本文使用快速算法仅需0.73 GB。
|
| 图 3 半径r=3.6λ金属球在φ=0平面双站RCS对比图 |
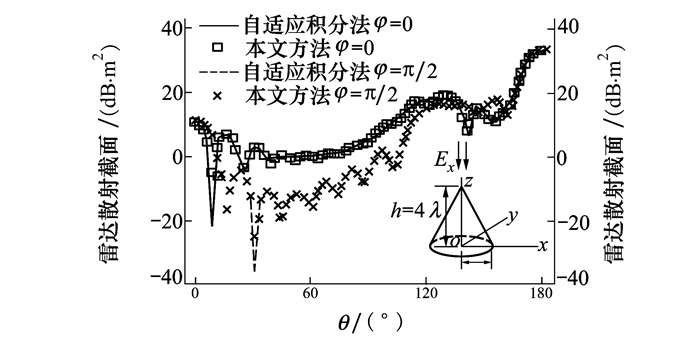
第二个算例是底面圆心位于原点的金属圆锥,其底面半径r=2λ,高h=4λ,模型示意图见图 4。经过剖分,在其表面共建立24 591个RWG基函数。如图 4所示,对于非球形的三维问题,本文的算法也与传统AIM计算结果相一致。
|
| 图 4 圆锥俯仰面双站RCS对比图 |
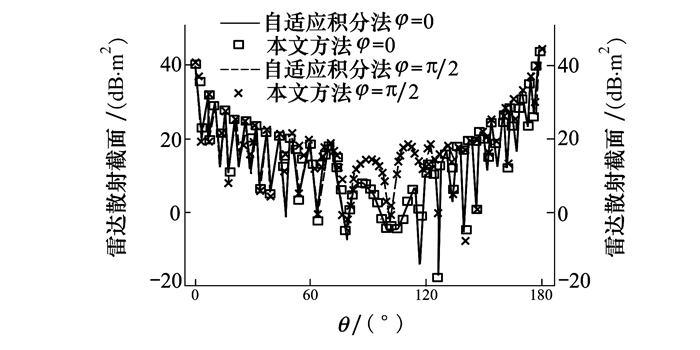
第三个算例是一个位于xoy平面截面为椭圆的面包圈形,内外径分别为5.4λ和6.6λ。椭圆短轴a=0.3λ沿z轴,长轴b = 0.6λ位于xoy面。剖分后未知量为51 582,从图 5可看出,对于这种扁平目标,本文的快速方法仍然与AIM能保持一致的结果。
|
| 图 5 截面为椭圆的面包圈形俯仰面双站RCS对比图 |
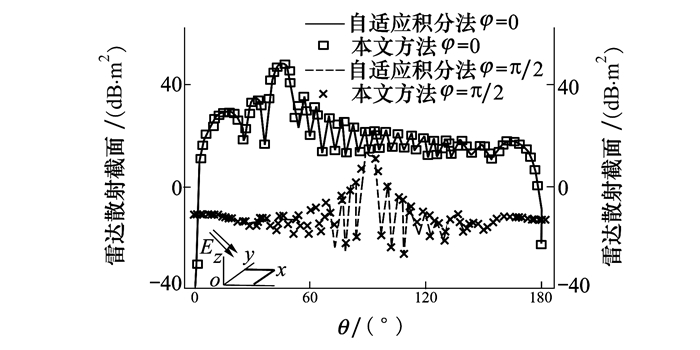
第四个算例是边长l =10λ的金属方形平板,平板位于xoy面且忽略厚度,未知量为30 013。与前3个算例不同,入射平面波为斜入射,其角度为(θ, φ)=(π/4, 0),模型示意图如图 6所示。从图 6可以看出,在φ = 0平面,最大散射方向为θ=-π/4,与入射波以平板法线相对称,这体现了电大尺寸的方形平板的光学偏转特性。而在φ =π/2平面,双站RCS最大辐射方向沿平板法线方向,并且呈现出对称特性。以上计算结果均与方形金属平板的特性相一致,从而验证了本文方法的精确性。
|
| 图 6 边长l=10λ方形金属平板俯仰面双站RCS对比图 |
在保证精度的前提下,本文的快速方法能够适用于不同形状的目标散射问题,计算结果与解析解和传统AIM相符。
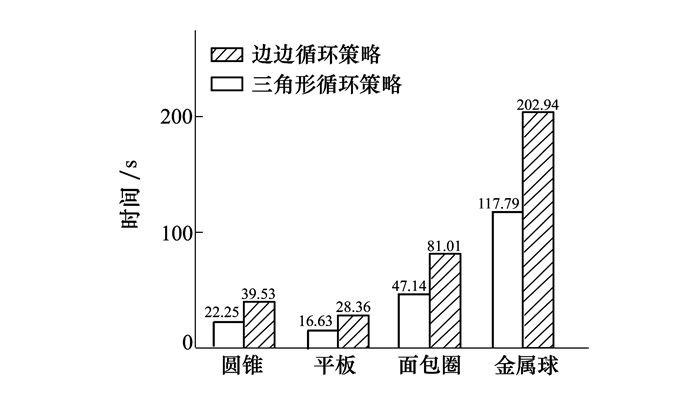
2.2 近场填充性能分析图 7对比了采用三角形循环策略和边边循环策略时,4个算例填充近场矩阵的计算时间。由于传统AIM的填充和矫正步骤是同时进行的,因此位于柱形图上方的时间仅代表填充和矫正的总时间,并不包括计算ILU预处理的时间。从图 7中可以得出,近区填充时间与近区元素个数成正比,虽然平板的未知数个数大于圆锥,但其近区填充时间反而小于圆锥。此外,4个算例都表明,三角形循环策略可以将填充速率提升至接近2倍。
|
| 图 7 近区矩阵计算时间对比图 |
根据(2)式可知,三角形循环策略中的公共积分共有4项,而边边循环策略中,每对三角形至多会被计算9次积分,因此从计算量上讲,填充速率最多提升至2.25倍。以上填充过程和分析,都是充分利用了阻抗矩阵对称性的前提下,仅计算上三角阻抗矩阵,并没有使用任何并行计算等加速手段。
本文采用的双重间距检测机制,能够最大限度的发挥三角形循环策略的优势,使其提升速率接近理论值。
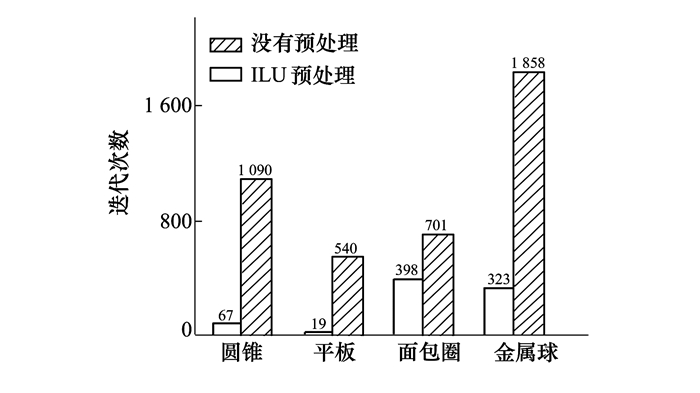
2.3 迭代求解收敛性分析图 8对比了4个算例在使用预处理前后的迭代收敛次数。从图中可以清晰看出,使用ILU预处理后,4个算例的迭代收敛速率全部得到不同程度提升。结合表 1可知,方形平板效果最好,经过预处理,其收敛速率提升至原来的20倍,圆锥得到了14倍的性能提升,最差的面包圈形也得到了1.76倍的提升。收敛速率提升的差异主要与模型的外形和大小有关,方形平板的阻抗矩阵元素排列规则,经过ILU预处理后,阻抗矩阵表现出显著的近对角占优特性,原本分散的矩阵特征值呈现出较好的谱聚特性,从而改善了矩阵的病态性。而对于面包圈,经过ILU处理后,因为矩阵的特征值谱聚特性提升较小,所以其收敛速率的提升比方形平板要小。此外,ILU预处理只与近场稀疏矩阵相关,因此可以适用于任意形状的目标散射体。
|
| 图 8 ILU预处理和没有预处理迭代次数对比图 |
| 算例 | 未知数 | 求解时间/s | 加速比 | |
| 使用ILU预处理 | 不使用预处理 | |||
| 圆锥 | 24 591 | 157.71 | 2 219.93 | 14.13 |
| 平板 | 30 013 | 7.87 | 161.53 | 20.45 |
| 面包圈 | 51 582 | 1 087.12 | 1 629.25 | 1.76 |
| 金属球 | 97 353 | 3 043.14 | 15 926.43 | 5.75 |
从表 1还可以看到,随着未知数个数的增多,迭代求解时间呈几何级增长。对于电大尺寸目标的散射问题,使用ILU预处理后,在迭代求解时,可以节省许多宝贵的时间。
3 结论本文利用三角形循环策略来提升AIM近场矩阵的填充速率。该方法将填充和矫正2个步骤分离,采用双重间距检测机制来确保填充时近场元素的正确性。随后,对未校验的近场矩阵进行ILU分解以提取预处理矩阵。最后完成近场矩阵的矫正并使用迭代法求解。仿真结果表明,该方法适用于分析任意形状的目标散射问题,并且在不影响精度的前提下,将近场矩阵的填充速率提升至原来的2倍,接近于理论提升上限,其中双重间距检测机制所占用的计算资源可以忽略不计。在使用ILU预处理后,其迭代收敛性也可以得到显著提升。但是,如果剖分单元大小相差过大,tnear需要谨慎选取,过大的tnear会在一定程度上降低近场填充速率。此外,使用ILU预处理需要额外的内存和计算量。因此,当N非常大时,必须在内存消耗和迭代速率间进行折衷选择。
总体上讲,本文的方法简单高效,适应性好,对电大尺寸目标RCS缩减,隐身性能评估,目标电磁散射特性快速分析等提供了有力支撑。
| [1] | HARRINGTON R F. Field Computation by Moment Methods[M]. NewYork, NY, USA: MacMillian, 1968 |
| [2] | WU L, ZHAO Y, CAI Q, et al. MLACE-MLFMA Combined with Reduced Basis Method for Efficient Wideband Electromagnetic Scattering from Metallic Targets[J]. IEEE Trans on Antennas and Propagation, 2019, 67(7): 4738-4747. DOI:10.1109/TAP.2019.2911352 |
| [3] | SEO S M, LEE J F. A Fast IE-FFT Algorithm for Solving PEC Scattering Problems[J]. IEEE Trans on Magnetics, 2005, 41(5): 1476-1479. DOI:10.1109/TMAG.2005.844564 |
| [4] | BLESZYNSKI E, BLESZYNSKI M, JAROSZEWICZ T. AIM:Adaptive Integral Method for Solving Large-Scale Electromagnetic Scattering and Radiation Problems[J]. Radio Science, 1996, 31(5): 1225-1251. DOI:10.1029/96RS02504 |
| [5] | OKHMATOVSKI V I, MORSEY J, CANGELLARIS A C. Loop-Tree Implementation of the Adaptive Integral Method(AIM) for Numerically-Stable, Broadband, Fast Electromagnetic Modeling[J]. IEEE Trans on Antennas and Propagation, 2004, 52(8): 2130-2140. DOI:10.1109/TAP.2004.832326 |
| [6] | KIM O S, MEINCKE P. Adaptive Integral Method for Higher Order Method of Moments[J]. IEEE Trans on Antennas and Propagation, 2008, 56(8): 2298-2305. DOI:10.1109/TAP.2008.926759 |
| [7] | LAI B, AN X, YUAN H B, et al. AIM Analysis of 3D PEC Problems Using Higher Order Hierarchical Basis Functions[J]. IEEE Trans on Antennas and Propagation, 2010, 58(4): 1417-1421. DOI:10.1109/TAP.2010.2041153 |
| [8] | RAUTIO B J, OKHMATOVSKI V I, CANGELLARIS A C, et al. The Unified-FFT Algorithm for Fast Electromagnetic Analysis of Planar Integrated Circuits Printed on Layered Media inside a Rectangular Enclosure[J]. IEEE Trans on Microwave Theory and Techniques, 2014, 62(5): 1112-1121. DOI:10.1109/TMTT.2014.2315594 |
| [9] | YANG K, YILMAZ A E. An FFT-Accelerated Integral-Equation Solver for Analyzing Scattering in Rectangular Cavities[J]. IEEE Trans on Microwave Theory and Techniques, 2014, 62(9): 1930-1942. DOI:10.1109/TMTT.2014.2335176 |
| [10] | WANG X, ZHANG S, LIU Z L, et al. A SAIM-FAFFA Method for Efficient Computation of Electromagnetic Scattering Problems[J]. IEEE Trans on Antennas and Propagation, 2016, 64(12): 5507-5512. DOI:10.1109/TAP.2016.2621028 |
| [11] | RAO S, WILTON D, GLISSON A. Electromagnetic Scattering by Surfaces of Arbitrary Shape[J]. IEEE Trans on Antennas and Propagation, 1982, 30(3): 409-418. DOI:10.1109/TAP.1982.1142818 |
| [12] |
韩国栋. 矩量法中阻抗矩阵的优化填充技术[J]. 微波学报, 2010(8): 15-19.
HAN Guodong. Optimization Technique on Filling Impedance Matrix in Moment Method[J]. Microwave Journal Dalian, 2010(8): 15-19. (in Chinese) |
| [13] | MEIJERINK J A, VAN DER VORST H A. An Iterative Solution Method for Linear Systems of Which the Coefficient Matrix is a Symmetric M-Matrix[J]. Mathematics of Computation, 1977, 31(137): 148. |


