2. 西北工业大学 力学与土木建筑学院, 陕西 西安 710129;
3. 内蒙古交通设计研究院有限责任公司, 内蒙古自治区 呼和浩特 010000;
4. 西北工业大学 航海学院, 陕西 西安 710072
索缆结构是现代结构承力体系的一个重要类型, 凭借其优美的建筑造型和良好的结构性能, 被广泛应用于大型工业厂房、大型场馆、高耸和大跨度桥梁等各类建筑结构中[1]。随着社会需求的增加, 大跨和高耸建筑大量出现, 结构用索的长度也在不断突破。随着长度的增加, 拉索及由其构成的索缆结构产生了一个突出问题:由于长细比大, 索结构的横向刚度和内阻尼很小, 因此在风荷载、移动荷载等的影响下, 容易产生各种类型的振动现象[2-3]。这些振动不仅会导致结构的动力稳定性和安全性问题, 而且会影响结构的疲劳耐久性和适用性。可见, 对于索缆结构体系, 其动力分析已成为此类工程结构的设计、运营期性能监控与维护以及振动控制的关键问题。随着索缆体系的结构日趋复杂, 其动力分析模型已经由最初基于不可伸长假定的张紧弦模型[4]、考虑垂度[5]和倾角[6]影响的弦模型, 发展至可伸长的弹性索模型, 以及考虑拉索抗弯刚度[7]、垂度[8]等多因素影响的欧拉梁模型。
已有索缆体系的动力分析理论按分析方法以及解的形式的不同可分为解析法、数值法、以及半解析半数值法, 其中解析法能够给出拉索系统动力特性或响应的显式解, 其解的形式简洁、直观, 因此在对拉索进行动力特性分析及参数识别时, 解析法有着广泛的应用[9-12]。然而传统的解析分析方法只能就拉索体系中的某些结构参数进行动力分析, 而无法全面考虑这些因素的影响, 故而所得结果的准确性、适用性也势必受到不同程度的影响; 为了全面考虑多种因素的影响, 与其他类型的工程结构一样, 索缆结构也可使用一些数值方法来解决其动力学分析问题, 包括有限元法[13]、Galerkin法[14]以及有限差分法[15-17]等, 其中有限元法使用较多。数值法的计算精度受限于索缆的离散程度和形函数的形式, 其精度和计算效率是难以调和的一对矛盾, 因此难以进行索缆结构的参数分析。鉴于此, 有必要提出一种既能全面考虑拉索设计参数影响, 又能兼顾计算精度和计算效率的分析方法。
为此, 本文将以动力刚度法为基础, 给出一种能同时考虑拉索抗弯刚度、垂度以及振动过程中索力增量等因素影响的分析方法。与此同时, 首次给出了小垂度拉索动刚度矩阵的显式解, 并通过Wittrick-Williams算法对频率方程进行精确求解[18], 从而有效避免了已有研究方法在频率求解中存在的“漏根”现象。
1 小垂度拉索力学模型索缆结构作为一种常见的工程结构, 其结构形式复杂, 对于类似输电电缆、系泊索等可被看作弦结构的拉索, 其抗弯刚度可以忽略, 此时几何大变形因素需要考虑。对于该类拉索, 需要从非线性运动方程出发研究其动力问题。然而, 对于短索或中长索, 常见的如拱桥和悬索桥的吊杆、斜拉桥的拉索等, 其抗弯刚度的影响必须考虑。该类拉索在自重作用下垂度较小, 垂跨比通常小于1/8, 即本文研究的小垂度索。在研究小垂度索的动力特性时通常采用小变形假定, 不考虑几何大变形的问题。
对于小垂度拉索系统, 已有研究工作已经可以考虑结构抗弯刚度、垂度、倾角中部分因素的影响, 但尚无法以解析或半解析的形式全面地考虑这些因素。鉴于此, 本文基于欧拉梁理论建立如图 1所示的考虑多参数影响的精细化拉索模型。图中, EI为索的抗弯刚度, H为索力, m为单位长度线质量, θ为拉索倾角, l为索长。由于实际工程中拉索通常较长, 其内阻尼往往可以忽略, 则小垂度索的控制微分方程为[8]
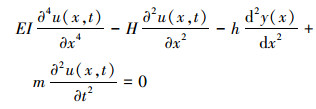
|
(1) |

|
| 图 1 同时考虑多参数影响的小垂度索力学模型 |
式中, h为由于拉索振动弹性伸长引起的附加索力。根据Ricciardi等人的研究, 如图 1所示, 在拉索二次抛物线静构型假设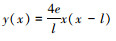
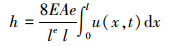
|
(2) |
式中:u(x, t)为拉索的动构型;垂跨比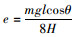
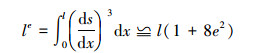
|
(3) |
式中,s代表拉索弧长。
对u(x, t)进行变量分离可得
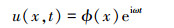
|
(4) |
令
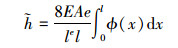
|
(5) |
将(4)式代入(1)式可得系统以幅值函数ϕ(x)描述的控制微分方程
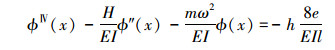
|
(6) |
引入无量纲参数: 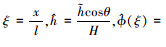
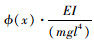
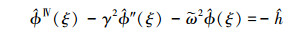
|
(7) |
式中: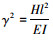
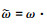
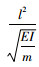
由此, (7)式的通解可表示为
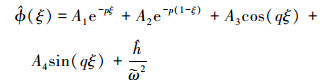
|
(8) |
需要说的是, (8)式中4个待定常数由拉索的边界条件决定。本文分析方法的一大优势是在分析时可对这些待定常数“设而不求”。如(16)式所示, 可将其用节点位移向量表示出来。而边界条件的影响则可方便地在集组总体动力刚度矩阵时考虑进来。
(8) 式的矩阵形式为
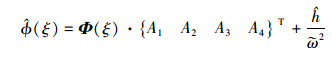
|
(9) |
式中
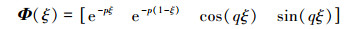
|
(10) |
式中
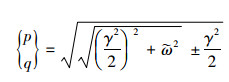
|
(11) |
而

|
(12) |
式中, 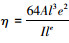
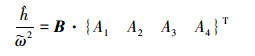
|
(13) |
式中, 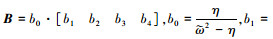
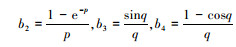
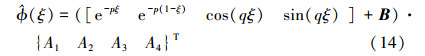
|
(14) |
根据节点力和位移函数的关系, 可以得到系统由振型函数表征的节点位移
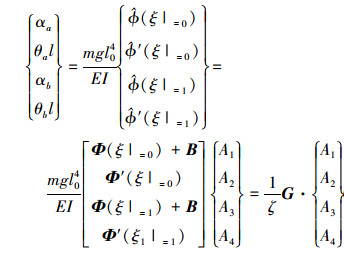
|
(15) |
式中, 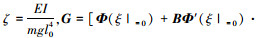
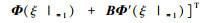

|
(16) |
结合结点力和位移的关系
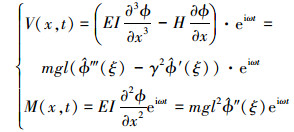
|
(17) |
以及振型函数(9)式可得
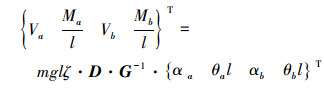
|
(18) |
式中,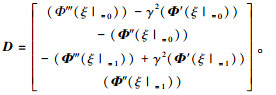
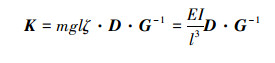
|
(19) |
在求得系统动刚度矩阵K后, 则系统的模态频率通常可由如下频率方程进行求解
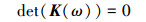
|
(20) |
式中,|·|表示行列式的值。满足上述频率方程的ω值即为系统的模态频率。通常情况下, 该频率方程为一复杂的超越方程, 在早期的研究中, 一些数学技巧被用来解决特定的简单结构的频率方程, 但实质上是通过零根搜索法来确定结构的各阶模态频率。这类方法是通过判断每次搜索的相邻2个试探解的函数值是否变号来求解频率, 不仅计算量大, 难于区分距离非常靠近的两阶模态频率, 亦无法区分零点和正负无穷处变号的情况, 因此很可能导致漏根的情况, Muller搜索法就属于此类方法范畴。为此, 就需要引入Wittrick-Williams(W-W)算法。
W-W是Wittrick和Williams在20世纪70年代提出的一种精确算法, 该方法可用于分析结构自由振动、屈曲问题和波传递问题。W-W算法在理论上解决了频率方程求解的漏根问题, 使得困扰DSM法多年的瓶颈问题得以解决, 推进了DSM理论的发展和工程应用。由于该方法可使动刚度矩阵保持Sturm序列特性, 能保证方程求解过程中不遗漏根, 其稳定性和正确性也在理论上被证明, 这是大多数解析法和近似解法所不具备的优点[20]。
应用W-W算法计算结构模态频率问题的关键步骤是确定结构的模态频率计数J, 它表示结构小于ω*的模态频率的个数。J一般难以直接求解, 但可通过另外2种计数之和来表示, 即
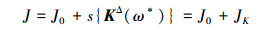
|
(21) |
式中:JK是和结构整体动刚度矩阵有关的计数, 它等于三角阵KΔ(ω*)主对角线上负元素的个数;KΔ(ω*)代表将结构的动刚度矩阵K(ω*)进行Gauss消元后形成的上三角矩阵;s{}为计数符号; J0是结构的固端频率计数, 它小于等于试探频率ω*的结构固端频率个数。结构固端频率是指将结构的边界条件全部固结后(称该结构为与原结构对应的固端结构)的模态频率, 可通过求解固端结构的频率方程(称为固端频率方程)得出。当结构因材料或截面不连续需要被分为若干个单元k时, 仿照结构固端频率计数J0的定义, 若用Jm表示单元的固端频率计数, 则二者的关系可表示为: 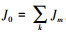
当求出结构在试探频率ω*下的固端频率计数J0(ω*)后, 即可按照(21)式求出结构小于试探频率ω*的模态频率的个数J(ω*)。此后若想计算结构的第i阶模态频率ωi, 则只需首先粗略地确定出该阶模态频率的上下界ωl和ωu, 使满足
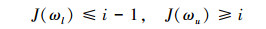
|
(22) |
则结构的第i阶模态频率满足ωi∈(ωl, ωu), 此后可采用二分法、牛顿法等数值方法, 通过不断调整上下界的值来逼近真实频率ωi, 当满足ωl-ωu≤Tol·(1+ωu)时, 可以得到允许误差范围Tol内的模态频率。
由于DSM适用于线性系统, 当考虑拉索垂度效应后系统将具有非线性特征, 此时系统动刚度矩阵不再严格对称, 也就无法直接应用W-W算法进行频率计算。然而对于小垂度拉索系统, 由于其弱非线性特点, 垂度对各阶模态频率的影响有限, 尤其对于高阶模态的影响几乎可以忽略。
基于这一特点, 可以做出如下假设:相比于无垂度系统(即h=0), 小垂度索缆系统的各阶模态频率ωsag与无垂度系统的模态频率ω0具有一一对应的关系, 即第n阶模态频率ωsag(n)将出现在ω0(n)的邻域内, 这一假设也是符合实际工程情况的。
基于上述假设, 本文结合改进W-W算法给出了一种适用于小垂度拉索体系的频率方程解法, 具体计算步骤如下:
1) 分别计算有无垂度系统和有垂度系统的系统动刚度矩阵K(ω)和Ksag(ω);
2) 应用改进W-W算法计算无垂度系统的第n阶模态频率ω0(n), 从而“锁定”小垂度系统的第n阶模态频率ωsag(n)可能落在的区间, 并以ω0(n)为初值在其邻域开始搜索ωsag(n);
3) 将ω0(n)代入动刚度阵Ksag并计算det(Ksag(ω0(n))), 若det(Ksag(ω0(n)))≤Tol则认为ωsag(n)=ω0(n), 这说明该垂度对系统该阶模态频率的影响很小。其中Tol为用户指定的误差限;
4) 若det(Ksag(ω0(n)))>Tol, 则需进一步判断搜索方向, 即判断|det(Ksag(ω0(n)))|和|det(Ksag (ω0(n)+Tol))|的大小。若|det(Ksag(ω0(n)))|> |det(Ksag(ω0(n)+Tol))|则不断增加初值直到相邻2步内有det(Ksag(ω0(n)+(m-1)Tol))×det(Ksag(ω0(n)+mTol)) < 0。此时停止搜索并输出ωsag(n)=ω0(n)+(m-0.5)Tol, 其中m为计算次数;
5) 若|det(Ksag(ω0(n)))| < |det(Ksag(ω0(n)+Tol))|, 则不断减小初值直到相邻2个搜索步内有det(Ksag(ω0(n)-(m-1)Tol))×det(Ksag(ω0(n)-mTol)) < 0此时停止搜索并输出ωsag(n)=ω0(n)-(m+0.5)Tol。
在上述求解步骤中, 首先通过W-W算法对小垂度系统的各阶模态频率进行了“定位”, 大大缩小了搜索范围, 从而提高了计算效率且避免了漏根的可能。
3 准确性验证为了说明本文所提出的改进W-W算法在计算小垂度拉索时的准确性, 方便起见, 以文献[8]中给出的2个拉索为例, 其参数见表 1, 文献[8]、原W-W算法以及本文提出的改进W-W算法的计算结果见表 2。
| 拉索 | m/kgm-1 | g/Nkg-1 | l/m | H/106N | E/Pa | A/m2 | I/m4 |
| 1 | 400 | 9.8 | 100 | 2.903 6 | 1.598×1010 | 7.850×10-3 | 4.953 5×10-6 |
| 2 | 400 | 9.8 | 100 | 26.132 5 | 2.082×1013 | 7.863×10-3 | 4.920 4×10-6 |
从表 2可以看出, 由于原W-W算法由于无法计入垂度影响, 其在计算低阶模态时容易产生较大误差, 而本文提出的改进W-W算法所得结果与文献结果更加接近, 从而说明了本文提出方法的计算精度。需要说明的是, 对于偶数阶模态而言, 由于拉索振型具有反对称特点, 其弹性伸长及附加索力h为0, 因此垂度将不会引起模态频率的改变, 此时3种方法的计算结果一致; 而对于奇数阶模态, 垂度对低阶模态的影响更为显著。
为了进一步说明本文提出方法在频率方程求解时的准确性, 以及以文献[8]为代表的一类解法在频率方程求解时存在的漏根可能性, 仍以上述拉索为例, 表 3同时给出了文献[8]、有限元解、以及张紧弦模型解。
| 模态 | 拉索1 | 拉索2 | |||||||
| 文献[8] | 弦理论 | 有限元 | 本文解 | 文献[8] | 弦理论 | 有限元 | 本文解 | ||
| 1 | 0.441 | 0.426 | 0.429 | 0.434 | 1.400 | 1.278 | 1.333 | 1.366 | |
| 2 | 0.855 | 0.852 | 0.853 | 0.855 | 2.682 | 2.556 | 2.682 | 2.682 | |
| 3 | 1.283 | 1.278 | 1.281 | 1.283 | 5.486 | 3.834 | 4.062 | 4.063 | |
| 4 | 1.710 | 1.704 | 1.708 | 1.710 | 6.970 | 5.112 | 5.486 | 5.486 | |
| 5 | 2.138 | 2.130 | 2.135 | 2.138 | 8.524 | 6.390 | 6.969 | 6.970 | |
| 6 | 2.566 | 2.556 | 2.563 | 2.566 | 10.162 | 7.668 | 8.524 | 8.524 | |
从表 3中可以看出:相比文献[8]方法, 本文提出的方法与有限元解吻合得很好, 说明本文提出方法在进行频率方程求解时具有更高的精度。此外, 对于表中拉索2的第三阶频率, 本文方法与有限元解一致, 同时参照弦理论可以判断出文献[8]算法遗失了第三阶模态, 所得频率实为该索的第四阶模态。
从上述分析可以看出, 本文提出方法较文献[8]不仅具有更高的计算精度, 还能够有效地避免在求解超越频率方程时的漏根可能性。此外, 当采用有限元法求解结构的高阶模态特性时往往需要加密单元划分, 这将导致计算效率的降低且计算精度难以保证; 与有限元不同的是, 本文采用方法在对结构进行动力分析时, 仅需在约束位置以及几何不连续处增设节点, 以本文讨论的拉索为例, 全索只需建立一个单元即可求解出各阶模态频率, 因此本文方法相比有限元法具有更高的计算效率。
4 结论本文基于动刚度理论首次推导出了考虑抗弯刚度和倾角等因素影响后, 小垂度拉索系统动刚度矩阵的显式解, 对原W-W算法进行改进, 使其适用于非线性系统频率方程的求解, 克服了已有研究在求解时的“漏根”现象。由于中间推导过程均是以解析形式给出的, 因此很大程度上提高了计算精度和效率。通过数值案例分析, 参考已有研究结果和有限元解验证了本文提出方法的正确性, 同时说明了已有分析方法在频率方程求解时存在的“漏根”现象。
需要说明的是, 本文旨在给出工程中一类小垂度拉索的动力分析方法, 而相关的参数分析不是本文的重点, 且由于本文的推导过程全部是解析的, 因此在推广至拉索的各类反问题时, 常见的如索力识别, 仍具有明显的理论优越性, 因此具有很好的工程应用价值。
| [1] | DAN Danhui, HAN Fei, CHENG Wei, et al. Unified Modal Analysis of Complex Cable Systems via Extended Dynamic Stiffness Method and Enhanced Computation[J]. Structural Control and Health Monitoring, 2019, 26(10): 2435. |
| [2] | HAN Fei, DAN Danhui. Free Vibration of the Complex Cable System-an Exact Method Using Symbolic Computation[J]. Mechanical Systems and Signal Processing, 2020, 139: 106636. DOI:10.1016/j.ymssp.2020.106636 |
| [3] | HAN Fei, DENG Zichen, Dan Danhui. A Novel Method for Dynamic Analysis of Complex Multi-Segment Cable Systems[J]. Mechanical Systems and Signal Processing, 2020, 142: 106780. DOI:10.1016/j.ymssp.2020.106780 |
| [4] | Routh E J. Dynamics of a System of Rigid Bodies[M]. Netherlands, Elementary Part, Kluwer Academic Publishers-Plenum Publishers, 1978: 156-156 |
| [5] | IRVINE H M. The Linear Theory of Free Vibrations of a Suspended Cable[J]. Proceedings of the Royal Society A, 1974, 341(1626): 299-315. |
| [6] | IRVINE H M. Free Vibrations of Inclined Cables[J]. Journal of the Structural Division, 1978, 104(2): 343-347. |
| [7] | MAIN J A, JONES N P. Vibration of Tensioned Beams with Intermediate Damper. Ⅰ:Formulation, Influence of Damper Location[J]. Journal of Engineering Mechanics, 2007, 133(4): 369-378. DOI:10.1061/(ASCE)0733-9399(2007)133:4(369) |
| [8] | RICCIARDI G, SAITTA F. A Continuous Vibration Analysis Model for Cables with Sag and Bending Stiffness[J]. Engineering Structures, 2008, 30(5): 1459-1472. DOI:10.1016/j.engstruct.2007.08.008 |
| [9] | HAN Fei, DAN Danhui, CHENG Wei. Exact Dynamic Characteristic Analysis of a Double-Beam System Interconnected by a Viscoelastic Layer[J]. Composites Part B:Engineering, 2019, 163: 272-281. DOI:10.1016/j.compositesb.2018.11.043 |
| [10] | HAN Fei, DAN Danhui, CHENG Wei. Extension of Dynamic Stiffness Method to Complicated Damped Structures[J]. Computers & Structures, 2018, 208: 143-150. |
| [11] | HAN Fei, DAN Danhui, CHENG Wei. An Improved Wittrick-Williams Algorithm for Beam-Type Structures[J]. Composite Structures, 2018, 204: 560-566. DOI:10.1016/j.compstruct.2018.07.108 |
| [12] | HAN Fei, ZHANG YingLuo, ZHANG Jubao, et al. Exact Dynamic Analysis of Shallow Sagged Cable System-Theory and Experimental Verification[J]. International Journal of Structural Stability and Dynamics, 2019, 19(12): P1950153. DOI:10.1142/S0219455419501530 |
| [13] | NI Y Q, CO J M, ZHEN G. Dynamic Analysis of Large-Diameter Sagged Cables Taking into Account Flexure Rigidity[J]. Journal of Sound & Vibration, 2002, 257(2): 301-319. |
| [14] | BOSTON C, WEBER F, GUZZELLA L. Optimal Semi-Active Damping of Cables:Evolutionary Algorithms and Closed-Form Solutions[J]. Smart Materials & Structures, 2009, 18(5): 055006. |
| [15] | LIU Z, CHEN G, ZHONG J. Application of Finite Difference Method in Measurement of Cable Tension by Vibration Method[J]. Journal of Basic Science & Engineering, 2007, 15(1): 104-110. |
| [16] | TABATABAI H, MEHRABI A B. Vibration Suppression Measures for Stay Cables[C]//International Conference and Exhibition on Electricity Distribution, 1999 |
| [17] | TABATABAI H, MEHRABI A B. Design of Mechanical Viscous Dampers for Stay Cables[J]. Journal of Bridge Engineering, 2000, 5(2): 114-123. DOI:10.1061/(ASCE)1084-0702(2000)5:2(114) |
| [18] | HAN Fei, DAN Danhui, CHENG Wei. An Exact Solution for Dynamic Analysis of a Complex Double-Beam System[J]. Composite Structures, 2018, 193: 295-305. DOI:10.1016/j.compstruct.2018.03.088 |
| [19] | HAN Fei, DAN Danhui, ZOU Yiqing, et al. Experimental and Theoretical Study on Cable-Supporting System[J]. Mechanical Systems and Signal Processing, 2020, 140: 106638. DOI:10.1016/j.ymssp.2020.106638 |
| [20] | HAN Fei, DAN Danhui, CHENG Wei, et al. A Novel Analysis Method for Damping Characteristic of a Type of Double-Beam Systems with Viscoelastic Layer[J]. Applied Mathematical Modelling, 2020, 80: 911-928. DOI:10.1016/j.apm.2019.11.008 |
2. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi'an 710129, China;
3. Inner Mongolian Transportation Design & Research Institute Co, Ltd, Hohhot 010000, China;
4. School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China


