在机器学习领域中, 离散型数据广泛适用于SVM、逻辑回归、KNN、决策树以及朴素贝叶斯等算法。其中SVM、逻辑回归及K最近邻算法对数据集特征的均一性十分敏感, 且决策树和贝叶斯算法只适合处理离散型数据。而在机器学习的实践应用中, 所获取数据集的属性多为连续型, 因此需对连续型属性进行一定的离散化处理[1]。实践表明, 离散化后的数据集均一性良好, 进行算法学习时, 训练的速度与精度会显著提升, 从而提高分类及预测性能。
连续属性离散化算法可分为无监督和监督离散化算法。无监督离散化以等间距算法为代表, 一般不考虑属性类别信息, 直接对其离散化, 效率高但精度差。而监督离散化算法涉及了属性类别信息, 时间与空间复杂度较高, 但离散化的结果更优, 其主要包括Skowron等人提出的基于布尔逻辑和粗糙集理论的离散化算法[2]、Liu等提出的Chi2算法[3]、Tay和Shen提出的Modified-Chi2算法[4]、谢宏等提出的基于信息熵的粗糙集连续属性离散化算法[5]、Kurgan等提出的基于CAIM统计量的离散化算法[6]、陈迎春等提出的一种基于K-means聚类的数据离散化算法[7]等。其中, 基于布尔逻辑和粗糙集理论的离散化算法, 由于其复杂度为指数级, 仅是理论上可行。基于信息熵的粗糙集连续属性离散化算法为每个候选断点定义信息熵, 再利用等价类进行划分, 可解决大数据量问题, 但并未考虑噪声数据的影响。Chi2算法和Modified-Chi2算法均是改进了chimerge离散化算法, 前者通过统计特征自动求取停止迭代的阈值, 后者在此基础上, 以近似分类质量替换不一致性指标, 减小了不确定性。CAIM算法根据数据集属性与类别间的相互依赖, 定义CAIM统计量, 但只提及了最多实例数的类别。基于K-means聚类的数据离散化算法, 以减小噪声、孤立点和不完备数据集对决策结果产生的影响, 但需要逐个属性离散化, 时间复杂度较高。
目前离散化技术主要采用单属性监督离散化算法, 上述算法均是单属性离散化, 忽略了属性间较强的关联性。而在机器学习的算法训练中, 数据集的最优离散化结果是多维属性的断点合集, 数目少而精度优。因此, 近年来多维属性的离散化成为数据挖掘的研究热点, 如Jiang等提出了基于粗糙集的多属性监督离散化(SMD)算法[8]、Wen等提出了一种基于信息熵的两阶段离散化(TSD)算法[9]、Sharmin等提出了基于互信息的特征选择与离散化(DSM)算法[10]等等, 均取得了一定成效。在多维连续属性上求取最优断点集已被证明是个NP问题, 群体智能算法也被广泛应用于求取近似最优断点集, 如遗传算法和粒子群算法[11]。
森林优化算法(forest optimization algorithm, FOA)是Ghaemi等于2014年提出的新的群体智能算法, 具有搜索效率高、不易陷入局部最优等特点, 可用于解决非线性优化问题[12]。而多维连续属性的离散化, 实则是通过一定算法选取断点, 对属性空间进行合理划分, 求取最优断点集, 以此优化机器学习的训练精度。基于此, 本文提出了一种基于森林优化的变精度粗糙集离散化算法, FORDA算法依据变精度粗糙集, 设计适宜值函数, 借助森林优化算法构建寻优网络, 在全局迭代搜索多维的最优断点子集。
1 粗糙集与森林优化算法粗糙集理论可用于处理不确定性问题, 在保持原有知识分类能力的前提下, 通过知识约简冗余信息, 以提高分类效率[13]。但粗糙集模型要求分类必须完全正确, 而实际数据中常含有噪音数据, 会导致对象所属类别误判。为克服其局限性, Ziarko提出了变精度粗糙集模型[14], 它的创新在于引入变精度参数, 允许一定程度的错误分类。变精度粗糙集已在模式识别、数据挖掘等领域广泛应用[15]。本文引入变精度粗糙集理论, 利用森林优化算法模拟种子传播过程, 全局搜索最优断点集。
1.1 变精度粗糙集模型设某信息系统可表示为S=(U, A, V, f), 其中:U是有限非空集合, 称为论域; f:U×A→V是信息函数; A为属性集合; 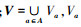

定义1 若集合X和Y为U的子集, p(X, Y)表示X关于Y相对错误率, 有
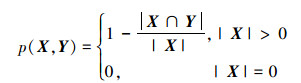
|
(1) |
式中, |X|代表集合X包含元素的个数。
定义2 多数包含, 指集合X中超过50%的元素包含在集合Y中, 对论域U中任意2个非空子集X和Y, 令0≤β≤0.5, 则多数包含关系定义为
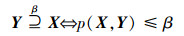
|
(2) |
式中,β为错误分类率。
定义3 对任意集合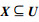

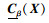
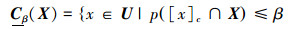
|
(3) |
下近似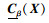
定义4 设决策属性D导出的对论域U的划分为
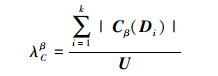
|
(4) |
近似依赖度λCβ表示决策属性D对条件属性集C中某属性的依赖程度, 表明了C对论域U中所含对象的分类能力。λCβ越趋于1, 则表明其分类能力越强。
1.2 森林优化算法森林优化算法是一种仿生类优化算法, 相较于遗传算法与粒子群算法, 该算法具有高搜索性能、更易获得全局最优等优点, 可用于求解NP难题及非线性连续型优化问题[16]。森林中种子传播分为本地播种和远地播种。本地播种即树木在其周边地域进行播种; 远地播种, 由于水流或大风等原因, 种子被散播到较远的土壤[12]。森林优化算法模拟种子传播, 搜寻生存条件优越的树木, 以求解问题的最优解。
该算法共有5个流程:初始化森林、本地播种、规模控制、远地播种和更新最优子树。以初始化并模拟森林作为开始步骤, 然后逐步进行本地播种、规模控制、远地播种等操作, 迭代产生新树而更新森林, 搜索求解最优子树[12]。算法中每棵树都设有年龄的上限参数, 初始年龄置0, 随着播种迭代, 树木年龄不断增加。对于超过年龄参数的树木, 就会将其去除, 按照一定概率选取使其形成候选森林。
2 FORDA算法设计森林优化算法模拟树木播种过程, 相比遗传算法和粒子群算法, 该算法不易陷入局部最优, 且搜索性能更佳[12, 16]。本文在多维连续属性上建立候选断点集, 通过模拟森林播种而迭代寻优, 求出最优断点子集。同时, 借助变精度粗糙集的分类容错特性, 设计适宜值函数, 以指导森林优化算法在全局进行多维寻优。
2.1 算法编码本文将离散化的断点集映射成森林中每棵树, 树木有年龄参数为Age, 一定数目的树形成森林。森林优化算法利用实数编码, 每棵树可作为一个一维数组Tree=[Age, v1, v2, …, vn][12]。其中除去年龄Age, v1到vi对应多维连续属性上候选断点集的断点取值, n为候选断点集的断点数目。i∈(1, n), 当vi取值不变, 说明选中该断点为最优断点子集中的一个断点, 当vi取“0”则表示去除该断点。由于数据集中连续属性值为0的情况极少, 故vi取值不为“0”, 即对于断点值为0的值, 不作处理。
森林迭代一次, 每棵树Age就增加1。Age有最大值, 称为“Life time”。对于Age值大于Life time的树, 将其去除出森林。每次迭代结束, 须更新最优解, 将其所对应树的Age置0, 并让其变成新树。
2.2 适宜值函数本文所提算法中, 适宜值函数既是衡量寻优性能的重要指标, 也是搜索是否停止的依据。即多次迭代后, 森林适宜值的变化值低于阈值η即视为找到最优解。考虑到森林群体的播种稳定, 森林整体的适宜值定义为:适宜值排在前m名的树, 取其适宜值均值。阈值η和m需在算法开始时设定。
近似依赖度越大, 说明属性子集对论域分类精度越高; 断点数目尽可能少, 则离散化效果越好。因此尽可能搜寻β数值大且断点数更少的断点子集[9]。据此, 以优化断点数目与近似依赖度为目的, 设E设为森林中树所对应的多维连续属性集C的断点集, 定义该树适宜值函数为

|
(5) |
式中, Eend为离散化后最优断点集, |E|与|Eend|表示离散化前后的断点集数目。依据λCβ判定当前数据集的决策能力, 以尽可能地优化断点数目; 并由|Eend|与|E|的比值调控断点数目, 避免对断点的盲目删减。则设森林的适宜值为
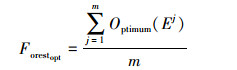
|
(6) |
每一次迭代后, 将森林中树的适宜值进行排序, 选取前m个, 其中Optimum(Ej)表示排名第j的树木适宜值, 其表示对应断点集的适宜值。
2.3 森林播种过程森林优化算法模拟种子传播寻找最优子树, 以此搜索问题的最优解。但由于不断的迭代播种, 导致树木数量急剧增大, 需对其数量进行合理调控。
2.3.1 本地播种本地传播(local seeding), 播种时绝大数种子散落在其附近, 树之间存在激烈竞争。本文模拟此过程, 将其用于最优断点集的局部寻优搜索。
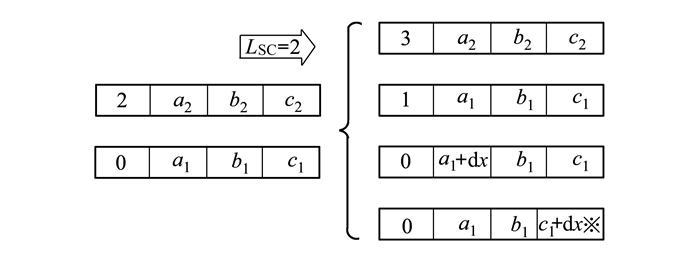
其具体过程如下:每棵Age为0的树先进行复制, 诞生一棵相同的新树, 后在该新树所有维中随机选择一维(不含Age维), 随机产生变化值dx∈[-Δx, Δx], 将dx加到被选中维的变量值上, 以改变该参数值, 诞生新树, 新树年龄均设为0, 并将其添加到森林里[12, 17]。其中, Δx较小, 每棵树播种产生的新树数目称作LSC(local seeding changes), LSC和Δx的值在算法运行时被给定。LSC取2时, 一次本地传播的过程, 如图 1所示。
|
| 图 1 本地播种过程 |
由于播种的持续进行, 森林中树木数量不断增加, 必须对森林规模进行控制。本阶段, 淘汰年龄过大和适宜值较小的树木, 形成候选森林, 用于远地播种。
2.3.3 远地播种远地播种(global seeding), 指种子会在距离树较远的区域生成新树。所提算法模拟远地播种过程, 进行全局搜索, 以克服本地播种可能陷入的局部最优。
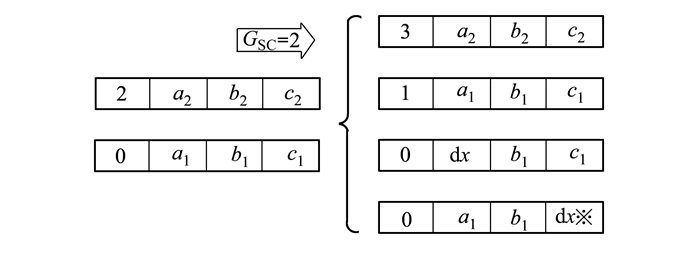
首先在候选森林中选取迁移概率为“rate”的树木, 进而在所选树的维度中, 随机选取GSC(global seeding changes)个维, 不含年龄维度; 每维均生成一个随机数, 并将该数赋给该维参数; 需注意, 生成的随机数须在合理的取值范围之内; 最后将诞生的新树加入森林中[12]。参数rate和GSC同LSC一样, 在算法运行前设定。GSC取2时, 一次远地播种的过程如图 2所示。
|
| 图 2 远地播种过程 |
本文提出的FORDA算法, 主要步骤包括计算候选断点集、初始化森林参数以及迭代求取最优解等步骤, FORDA流程图如图 3所示。

|
| 图 3 FORDA流程图 |
设需要离散化的数据集为Data, 具体的算法流程描述如下:
输入:需要离散化的数据集Data
输出:森林最后一次播种中, 选取适宜值最大的树, 其对应的断点集即为全局最优断点集
1) 提取Data的条件属性及决策属性等关键因子, 构建决策信息系统S, 计算候选断点集Eh;
2) 初始化森林参数, 预设定森林适宜值参数m与阈值η、树数目Tnum、树的最大年龄Life-time、森林适宜值Forestopt、候选断点集个数n、本地播种参数LSC和Δx、远地播种参数GSC、迁移概率rate以及多数包含关系β等参数值; 则树的编码维度为n+1;
3) 随机产生Tnum个维度为n+1的实数编码树;
4) for i=1, 2…Tnum
5) 将森林中树Ti映射成断点集;
6) end for
7) While森林适宜值Forestopt变化值>阈值η:
8) 执行本地播种, 更新森林参数, 去除老化的树, 更新候选森林;
9) 执行远地播种, 更新森林参数, 计算各个树Ti的适宜值;
10) 根据树的适宜值, 计算并更新森林适宜值;
11) end While
12) 得到最优森林, for i=1, 2…Tnum
13) 计算Optimum(Ei)并排序;
14) end for
15) 适宜值为max(Optimum(Ei))的树, 即为最优树, 其对应多维最优断点集Eopt;
综上所述, FORDA算法的重点在于采用粗糙集构建初始的候选断点集, 定义树的适宜值函数, 并将其融入森林优化算法, 进行迭代寻优。步骤2)中, 特别是树的最大年龄Life-time、本地播种LSC、远地播种GSC等参数, 对FORDA算法的性能影响较大, 需要通过经验选择或相关试验确认。而在步骤3)中, 每棵实数编码树均代表一个独立的候选解空间, 进而由后续的步骤7)至步骤15), 通过局部的本地播种与全局的远地播种, 以此迭代森林, 得到最优解。
3 实验连续属性离散化属于机器学习的数据预处理, 对其算法的评价, 主要是考察离散化后的数据集对算法分类或预测的精度是否有提升[18-20]。故而本文进行了2个实验, 实验1采用SVM分类器, 训练FORDA算法离散化后的数据集, 分析SVM的分类精度是否提高; 实验2则采用Cart决策树分类器, 对比数据集离散化前后的C4.5训练时间长短。分别在5个数据集上, 对比了本文FORDA算法和其他4种主流算法的离散化效果, 来验证所提算法的有效性。其中, SVM分类器采用间接法实现二分类或多分类的任务。
本文实验中的各算法均采用Python3实现, 在Pycharm里集成anaconda编程环境, 计算机的基本配置:CPU为I5-4560处理器, 主频2.6 GHz, 内存为8 G。FORDA算法基本参数预设如下:森林适宜值参数m=10, 森林适宜值Forest-opt=2, 算法停止阈值η=0.1, 树的最大年龄Life-time=6, 森林中初始树数量Tnum=30, 本地播种参数LSC=2, 远地播种参数GSC=1, rate=10%以及多数包含关系β=0.15。需说明, 算法参数值的设定依赖于经验选择与相关实验的筛选。
3.1 数据集数据集的选取对算法的训练效果有直接影响, 首先从UCI中选取了Iris、Flags、breast、Adult以及Heart-disease等5个广泛应用的数据集。表 1表示了所选数据集的信息, 如样本大小、连续型属性数目以及决策属性类别数等等。
| 数据集 | 信息 | ||
| 样本大小 | 决策属性类别数 | 连续属性数目 | |
| Iris | 150 | 3 | 4 |
| Flags | 194 | 8 | 2 |
| Breast | 699 | 2 | 9 |
| Adult | 48842 | 2 | 6 |
| Heart-disease | 270 | 2 | 6 |
本文所选取的数据集中, Iris连续型属性较少, Heart-disease数据集连续属性较多, Flags决策属性类别数较多, 而Breast决策属性类别较少, Adult数据集的样本数目巨大。数据集的迥然不同, 有助于测试并对比各算法的性能差异。实验中每个数据集随机打乱, 取前80%作为训练集, 余下作为测试集。
3.2 实验1实验1通过SVM多分类器, 对FORDA算法离散化后的数据集进行训练, 对比分类精度, 比较所提算法和Modified-Chi2算法、CAIM算法、SMD算法以及TSD算法的性能。其中, Modified-Chi2算法和CAIM算法是单属性离散化算法, SMD算法和TSD算法均是多属性离散化算法, 对比算法的多样性, 增强了实验结果的说服力。
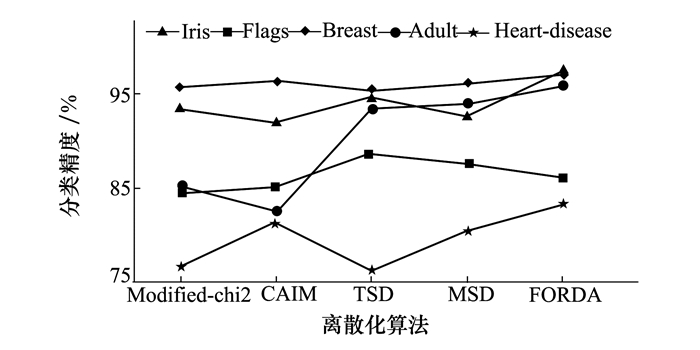
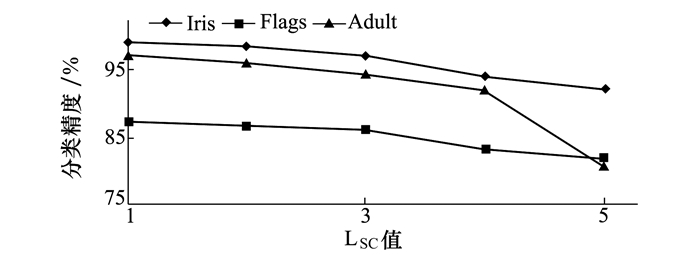
实验1结果如表 2所示。表 2是同一条件下, 所提FORDA算法与其他4种算法, 利用SVM分类器分类的精度对比。依据表 2数据, 图 4是各算法的SVM分类精度对比图。图 5表示在不同的本地播种参数LSC值下, 本文算法对Iris、Flags和Adult 3个数据集的分类精度。
| 数据集 | 算法 | ||||
| Modified-chi2 | CAIM | TSD | SMD | FORDA | |
| Iris | 93.3 | 92.0 | 94.7 | 92.7 | 97.3 |
| Flags | 84.5 | 85.1 | 88.7 | 87.6 | 89.2 |
| Breast | 95.7 | 96.3 | 95.3 | 96.1 | 95.5 |
| Adult | 85.1 | 82.6 | 93.5 | 94.0 | 95.8 |
| Heart-disease | 76.7 | 81.5 | 76.3 | 80.7 | 83.3 |
| 平均分类精度 | 87.1 | 87.5 | 89.7 | 90.2 | 92.2 |
|
| 图 4 各算法SVM分类精度 |
|
| 图 5 不同LSC值下的分类精度 |
由图 4可看出, 除在Breast数据集上, 本文算法的SVM的分类精度均是最高。在Adult和Heart-disease数据集上, 相对其他算法, 本文算法的性能提升明显, 只有SMD的各项分类精度较为接近本算法。
表 2表明各算法在5个数据集上的SVM平均分类精度, FORDA、SMD以及TSD等多维属性离散化算法的SVM分类精度远高于单属性离散化算法。而本文所提的FORDA算法的平均分类精度最高, 为92.2%, 相比其他算法提升2.2%到5.9%不等, 性能最佳, 离散化成效显著。
图 5表明, 在Iris等3个数据集下, 随着森林优化算法的本地播种参数LSC值的增大, FORDA算法的SVM分类精度呈现下降趋势。当LSC取值为1时, FORDA算法的SVM分类精度在5个数据集上达到峰值, 整体性能最优; 而LSC取值为2时, 算法性能也与其基本一致。本文算法预设参数的选值不同, 使得离散化区间、离散化后断点数目有差异, 从而影响机器学习的分类精度。
实验1表明, 相较于CAIM等主流离散化算法, 本文所提的FORDA算法离散化性能表现优异, 对于机器学习的分类精度有显著提升。
3.3 实验2实验2采用了Cart分类器, 由于Iris与Flags样本数目小, 训练时间太短, 区分度过小, 因此实验2仅采用Breast、Heart-disease以及Adult数据集, 在此3个数据集上, 对比离散化前后的Cart分类器训练时间长短, 验证所提算法的有效性。
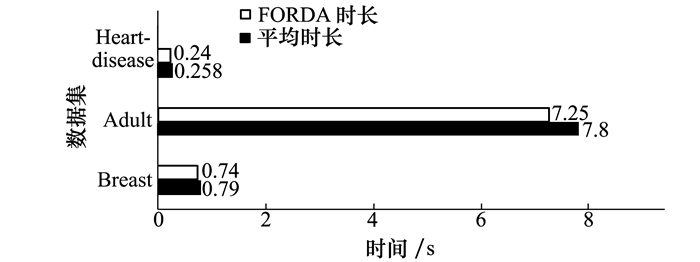
实验结果如下, 表 3表示所提FORDA算法与其他4种算法, 利用Cart分类器的训练时长。表中“无”为未使用离散化算法的Cart分类器训练时长, 仅采用基尼指数对连续值进行处理。图 6为FORDA算法的Cart训练时长与5种算法平均时长对比图。
| 数据集 | 算法 | |||||
| 无 | Modifed-chi2 | CAIM | TSD | SMD | FORDA | |
| Breast | 0.9 | 0.84 | 0.89 | 0.72 | 0.75 | 0.74 |
| Adult | 11.23 | 8.16 | 8.21 | 7.51 | 7.89 | 7.25 |
| Heart-disease | 0.34 | 0.27 | 0.28 | 0.24 | 0.26 | 0.24 |
|
| 图 6 FORDA时长与平均时长对比 |
由表 3可看出, 采用离散化算法后, Cart分类器的训练时长显著降低。除在Brest数据集上, 所提的FORDA算法训练时长均为最低。图 6表明, 5种离散化算法在3个数据集上, Cart分类器平均训练时长为0.79 s, 7.8 s和0.258 s, 而FORDA算法的Cart训练时长相对缩短6.3%~7.1%, 远低于平均时长, 性能有较大提升。
实验2表明离散化处理对机器学习算法的时间效益有较大提升, 而相较于其他4种算法, 本文所提的FORDA算法表现更佳。
此外, 同样在经典的C4.5分类器及BP深度神经网络上, 分别对CAIM、基于改进K-means聚类算法的数据离散化(K-means)、DSM以及本文所提的FORDA等算法进行了分类精度与训练时长的相关实验, 数据集采用了Iris、Breast及Adult。如表 4所示, 较于其他3种算法, FORDA算法对C4.5平均分类精度提升1.3%~3.7%, 平均训练时长缩短了3.0%~7.4%;BP神经网络的平均分类精度提升了2.0%~4.5%, 训练时长则缩短了3.2%~8.4%。这表明了FORDA具有一定的通用性, 能提升常用的机器学习算法的分类精度并降低训练时长。
| 算法 | 比较类型 | |||
| C4.5平均分类精度/% | BP平均分类精度/% | C4.5平均训练时长/s | BP平均训练时长/s | |
| CAIM | 88.7 | 90.3 | 5.85 | 7.23 |
| K-means | 89.5 | 92.8 | 5.71 | 6.84 |
| DSM | 91.1 | 92.5 | 5.59 | 6.97 |
| FORDA | 92.4 | 94.8 | 5.42 | 6.62 |
本文提出了一种基于森林优化的属性离散化算法, 依据粗糙集理论设计适宜值函数, 并在森林寻优网络中迭代搜索最优断点集。实验采用UCI中5个有显著差异的数据集, 对本文所提的FORDA算法进行验证。实验结果表明, 相对于当前主流的离散化算法, 本算法的SVM平均分类精度提升2.2%~5.9%, 且离散化后, Cart分类器训练时长较平均时长缩短6.3%~7.1%。其离散化效果较优, 且同样适用于BP神经网络与C4.5分类器, 具有一定的通用性, 可作为机器学习领域一种优良的数据集预处理方法。但本文算法的参数值预设定较为重要, 需进行相关实验来抉择。如何合理设定LSC等参数, 这将是未来的研究方向。
| [1] | YANG Y, WEBB G I, WU X. Discretization Methods Data Mining and Knowledye Discovery Handbook[M]. Boston: Springer, 2009. |
| [2] | PAWLAK Z, SKOWRON A. Rough Sets and Boolean Reasoning[J]. Information Sciences, 2007, 177(1): 41-73. |
| [3] | LIU H, HUSSAIN F, TAN C L, et al. Discretization:an Enabling Technique[J]. Data Mining and Knowledge Discovery, 2002, 6(4): 393-423. DOI:10.1023/A:1016304305535 |
| [4] | TAY F E H, SHEN L. A Modified Chi2 Algorithm for Discretization[J]. IEEE Trans on Knowledge and Data Engineering, 2002, 14(3): 666-670. DOI:10.1109/TKDE.2002.1000349 |
| [5] |
谢宏, 程浩忠, 牛东晓. 基于信息熵的粗糙集连续属性离散化算法[J]. 计算机学报, 2005, 28(9): 1570-1574.
XIE Hong, CHENG Haozhong, NIU Dongxiao. Discretization Algorithm for Continuous Sets of Rough Sets Based on Information Entropy[J]. Journal of Computers, 2005, 28(9): 1570-1574. (in Chinese) DOI:10.3321/j.issn:0254-4164.2005.09.021 |
| [6] | KURGAN L A, CIOS K J. CAIM Discretization Algorithm[J]. IEEE Trans on Knowledge and Data Engineering, 2004, 16(2): 145-153. DOI:10.1109/TKDE.2004.1269594 |
| [7] |
陈迎春, 李鸥, 孙昱. 基于聚类离散化和变精度邻域熵的属性约简[J]. 控制与决策, 2018, 33(8): 1407-1414.
CHEN Yingchun, LI O, SUN Yu. Attribute Reduction Based on Clustering Discretization and Variable Precision Neighborhood Entropy[J]. Control and Decision, 2018, 33(8): 1407-1414. (in Chinese) |
| [8] | JIANG F, ZHAO Z, GE Y. A Supervised and Multivariate Discretization Algorithm for Rough Sets[C]//Rough Set & Knowledge Technology-International Conference, 2010 |
| [9] | WEN L Y, MIN F, WANG S Y. A Two-Stage Discretization Algorithm Based on Information Entropy[J]. Applied Intelligence, 2017, 47(1): 1-17. |
| [10] | SHARMIN S, ALI A A, KHAN M A H, et al. Feature Selection and Discretization based on Mutual Information[C]//IEEE International Conference on Imaging, 2017 |
| [11] |
张婧, 曹峰, 唐超. 基于遗传算法和变精度粗糙集的离散化算法[J]. 华中师范大学学报, 2018, 52(3): 36-42.
ZHANG Jing, CAO Feng, TANG Chao. Discretization Algorithm Based on Genetic Algorithm and Variable Precision Rough Set[J]. Journal of Huazhong Normal University, 2018, 52(3): 36-42. (in Chinese) |
| [12] | GHAEMI M, FEIZI-DERAKHSHI M R. Forest Optimization Algorithm[J]. Expert Systems with Applications, 2014, 41(15): 6676-6687. DOI:10.1016/j.eswa.2014.05.009 |
| [13] | PAWLAK Zdzisław. Rough Sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356. |
| [14] | ZIARKO W. Variable Precision Rough Set Model[J]. Journal of Computer & System Science, 1993, 46(1): 39-59. |
| [15] | JIA X, LIAO W, TANG Z, et al. Minimum Cost Attribute Reduction in Decision-Theoretic Rough Set Models[J]. Information Sciences, 2013, 219(Complete): 151-167. |
| [16] | CHAGHARI A, FEIZI-DERAKHSHI M R, BALAFAR M A. Fuzzy Clustering Based on Forest Optimization Algorithm[J]. Journal of King Saud University-Computer and Information Sciences, 2018, 30(1): 25-32. DOI:10.1016/j.jksuci.2016.09.005 |
| [17] |
聂大干.森林优化算法的改进及离散化研究[D].兰州: 兰州大学, 2016 NIE Digan. Improvement and Discretization of Forest Optimization Algorithms[D]. Lanzhou: Lanzhou University, 2016(in Chinese) |
| [18] | JIANG F, SUI Y. A Novel Approach for Discretization of Continuous Attributes in Rough Set Theory[J]. Knowledge-Based Systems, 2015, 73: 324-334. DOI:10.1016/j.knosys.2014.10.014 |
| [19] | CLÁÁUDIO Rebelo de Sá, SOARES C, KNOBBE A. Entropy-Based Discretization Methods for Ranking Data[J]. Information Sciences, 2016, 329: 921-936. DOI:10.1016/j.ins.2015.04.022 |
| [20] | KHANMOHAMMADI S, CHOU C A. A Gaussian Mixture Model Based Discretization Algorithm for Associative Classification of Medical Data[J]. Expert Systems with Applications, 2016, 58: 119-129. DOI:10.1016/j.eswa.2016.03.046 |




