无人机系统是目前无人系统领域发展最快、水平最高、实际应用最多的一类空中无人系统, 具有成本低、无人员伤亡、操作方便和灵活可靠等特点。随着应用环境的日趋复杂, 以及任务的日益多样, 单机的能力受到了限制, 多机的编队协同已经成为无人机应用的重要发展趋势。一组低成本的无人机可以代替昂贵的多功能无人机, 实现大规模分布式高精度探测, 降低任务成本, 提高任务成功率。
与固定翼飞机相比, 四旋翼飞机具有许多优点, 例如, 利用它的4个旋翼和小尺寸等优点, 可以执行垂直起飞、着陆、悬停以及室内飞行的能力。得益于一致性理论的快速发展, 及其在多智能体控制方面的成功应用, 基于一致性理论的多无人机编队控制展现出了巨大的潜力。通过无人机之间的信息交互, 使得编队中的无人机达到状态的协同一致, 成为无人机编队方式的热门研究方向。信息交互是保证多无人机编队安全稳定控制的前提, 然而编队内无人机之间的通信总会受到天气、电磁干扰、网络拥堵、通信设备间歇性故障等因素的影响, 而使信息交互存在延迟。尽管现存的一些优化控制方法本身具有一定鲁棒性, 能够在一定程度减小乃至消除通信时延的影响, 但是当通信延迟较大时这些控制方法很可能无法保证编队内无人机之间正常信息交互以致编队失控, 因此研究存在通信时延条件下的编队控制具有十分重要的现实意义。
Redrovan等[1]提出了基于主机-僚机原理的编队控制和轨迹跟踪的滑模控制器的设计; Guerrero等[2]开发了一种基于分离饱和度的非线性控制器, 用于微型四旋翼的基于主机-僚机网络的多智能体一致性算法, 但实验结果只包括偏航角的一致性; 王品等[3]在不考虑时延和噪声等干扰的理想情况下, 利用具有虚拟领航者的二阶动态一致性协议讨论了三维空间内分布式无人机编队控制问题; 熊涛等[4]针对多无人机系统的编队控制问题, 提出了一种基于级联系统理论及输入约束一致性算法的控制方法。以上文献只是在理想情况下对编队控制或者一致性编队进行了介绍, 或者只考虑了部分约束, 并没有涉及编队和无人机所受到的约束。
Zhu等[5]提出了一种具有自延迟和不确定性的自适应控制算法, 以保证多智能体全局全状态的同步; 王品等[6]在高阶一致性理论的基础上, 得出了具有时变时延导数信息及无导数信息情况下的稳定性充分条件; 李少斌等[7]在一致性协议的基础上提出了分布式的编队控制算法, 并分析了时延多无人机系统的稳定性; Hou等[8]给出了具有通信延迟的一般二阶多智能体系统的一致性条件; 张汝波等[9]系统地讨论存在时延的编队控制系统的稳定性问题; 文献[10-14]也做了大量相关的工作。以上文献对于编队的延时问题做了研究, 但也大多是基于相对简单的模型, 并没有考虑复杂智能体的非线性特性以及干扰因素的存在。
本文在探讨三维空间的无人机编队问题的基础上, 同时考虑编队过程中的通信时延以及干扰的影响。首先基于一致性理论设计多无人机编队控制的协议, 并给出存在时延情况下, 计算延时裕度的具体公式; 然后针对无人机受到的干扰, 设计相应的滑模控制器, 在实现无人机编队一致性的基础上, 也能够保持对于外部干扰的鲁棒性。
1 带干扰的四旋翼动力学模型本文考虑的四旋翼结构是完全相同的。正如文献[15]介绍的, 四旋翼的动力学模型可以通过拉格朗日方法获得。这里, 考虑干扰因素的四旋翼非线性数学模型如(1)式所示
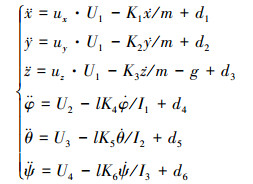
|
(1) |
式中:(x, y, z)为四旋翼的质心在惯性坐标系中的位置坐标; (φ, θ, ψ)为四旋翼的3个姿态的欧拉角, 分别代表滚转角、俯仰角和偏航角; Ki(1, …, 6)为阻力系数; m为四旋翼无人机的负载总质量; g是重力加速度; l为四旋翼的每个旋翼末端到飞行器重心的距离; Ii(i=1, 2, 3)分别为围绕每个轴的转动惯量; Ui(i=1, 2, 3, 4)为对应的控制器; di(i=1, 2, …, 6)表示扰动, 且|di|≤Di, Di(i=1, 2, …, 6)为有界正实数。ux、uy和uz的表达式如(2)式所示
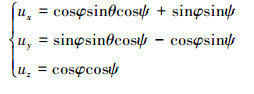
|
(2) |
考虑由n架无人机在三维空间里构成的系统, 每架无人机由Vi(i∈{1, 2, …, n})表示。它们构成的有向图记为G={V, E, A}, 其中, 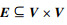
这里, 度矩阵表示为D=diag{d1, d2, …, dn}, 其中, 对角元素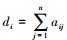
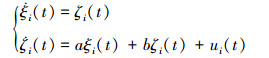
|
(3) |
式中:ξi(t)∈R3表示第i个UAV的位置状态, ζi(t)∈R3表示第i个无人机状态的导数;ui(t)则表示第i个无人机的控制输入。
本文只考虑定常时延的情况, 为了使得多架无人机能够按照期望的编队进行飞行, 假设ξ0∈R3和ζ0∈R3分别为期望编队的几何中心对应的位置和速度, 在只考虑定拓扑结构的定常系统时, 二阶系统连续时间的一致性方法为

|
(4) |
式中:k1>0, k2>0为增益系数;pi∈R3为对应无人机期望的位置;pij=‖pi-pj‖为无人机之间期望的距离;τ为延迟时间。需要指出的是, 在控制决策中对于节点i也使用了相同的延迟时间τ, 这是为了保证在反馈中误差信号的准确性, 进而保证编队系统的一致性。
2.2 具有定常时延的一致性条件定义状态向量z(t)=[ξT(t), ζT(t)]T, 其中, ξ(t)=[ξ1(t), ξ2(t), …, ξn(t)]T为位置向量, ζ(t)=[ζ1(t), ζ2(t), …, ζn(t)]T为速度向量。从而多无人机系统的状态方程转换为
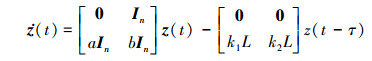
|
(5) |
令ξie(t)=ξi(t)-pij-ξ1(t), ζie(t)=ζi(t)-ζ1(t), 则状态误差向量为ze(t)=[ξeT(t), ζeT(t)]T, 其中, ξe(t)=[ξ2e(t), ξ3e(t), …, ξne(t)]T, ζe(t)=[ζ2e(t), ζ3e(t), …, ζne(t)]T, In为n维单位矩阵, 0表示适当维数的零矩阵, 从而可以得到以下多无人机系统的误差动力学方程
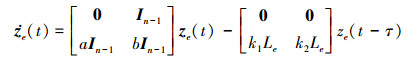
|
(6) |
式中:Le=L22+In-1αT;In-1表示所有n-1个元素都为1的列向量, 这里的L22和α表示如下
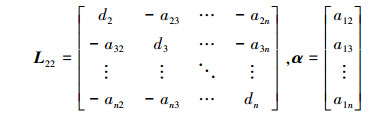
|
显然, 当且仅当误差系统(6)是渐进稳定的, 控制律(4)能够使系统(3)或者(5)实现一致性。为了分析系统(6)的渐进稳定性, 考虑其特征方程如下
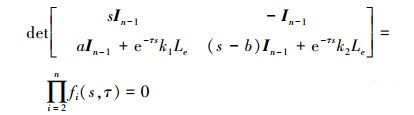
|
(7) |
式中,fi(s, τ), (i=2, 3, …, n)为准多项式, 其表达式如下
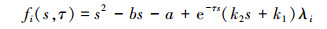
|
(8) |
根据文献[16]的结论, 可以知道:
定理1 当且仅当所有准多项式(8)都是Hurwitz稳定(即它们的根都具有负实部)时, 控制律(4)能够使系统(3)在具有通信延迟τ的情况下实现一致性。
推论1 若(3)中的a=b=0, 也即(3)式为双积分模型时, 当且仅当所有准多项式fi(s, τ)=s2+e-τs(k2s+k1)λi=0, (i=2, 3, …, n)为Hurwitz稳定时, 控制律(4)能够使系统(3)在具有通信延迟τ的情况下实现一致性。
定理2 假如控制律(4)能够使系统(3)在没有延迟的情况下实现一致性, 则对于任意r∈{2, 3, …, n}, 令ωr>0为如下方程的根
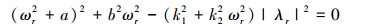
|
(9) |
令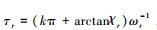
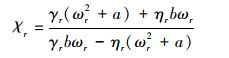
|
(10) |
式中:γr=k2ωrRe(λr)+k1Im(λr);ηr=k2ωr·Im(λr)-k1Re(λr);其中, Re(λr)和Im(λr)分别是λr的实部和虚部;k是能够使τr>0成立的最小整数。令τ*=minτr(所有令ωr>0的值), 则当且仅当τ∈[0, τ*)时, 控制律(4)能够使系统(3)实现一致性。
特殊情况, 当a=b=0时, 也即系统为双积分器模型时, 则能够得到以下结论:对于任意r∈{2, 3, …, n}, 有
注意 定理2给出了二阶一致性编队问题中所允许的最大通信延迟时间。
3 控制方法的实现对于非线性系统的简化会使得系统的动态特性不够精确或者引起参数的不确定性, 滑模控制(SMC)是一种算法简单而鲁棒性强的控制方法, 不仅能够有效地实现对线性和非线性系统的控制, 而且对外部的干扰拥有很强的鲁棒性。所以, 本文采用滑模控制方法来进行控制器的设计。
由四旋翼飞行器的动态模型可以知道, 输入量有4个, 而输出量有6个, 这意味着无法同时控制所有无人机的状态。由于欠驱动特性的存在, 不可能对6个输出量都进行跟踪, 一个合理的控制方案是跟踪轨迹和滚转角, 也即变量(x, y, z, φ), 同时保证俯仰角θ和偏航角ψ的稳定[17]。
首先, 通过设计位置控制律, 以实现无人机对于位置的跟踪。由(1)式定义
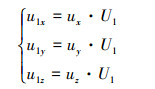
|
(11) |
因此用来描述位置状态的子系统为
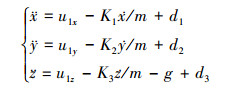
|
(12) |
假设期望的位置坐标为(xd, yd, zd), 针对(11)式设计的滑模函数分别为
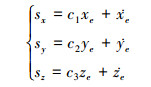
|
(13) |
式中:xe=x-xd; ye=y-yd; ze=z-zd; c1>0;c2>0;c3>0。
以x轴为例, 由李雅普诺夫理论可知, 要使该状态在xe=0处稳定, 选取李雅普诺夫函数V(sx)= 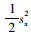
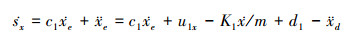
|
(14) |
设计滑模控制律为
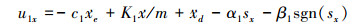
|
(15) |
式中:α1>0;β1≥D1>0;sgn(·)为符号函数。则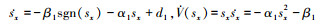


同理, 可以得到y和z状态的控制律, 如(16)和(17)式所示
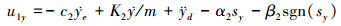
|
(16) |
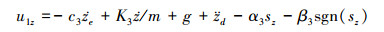
|
(17) |
式中:α2>0;β2≥D2>0;α3>0;β3≥D3>0。同样, y和z能够分别指数收敛于yd和zd。
在实现SMC时, 由于存在滑动面上的高频切换, 其中的一个缺点是存在抖动效应, 可以定义为系统的无限振荡。为了最大限度地减少抖动, 用F(·)代替式中的sgn(·)函数。其中, F(·)为饱和函数, 具体表达式如下
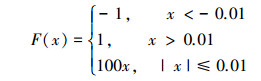
|
(18) |
假设满足控制律(15)、(16)和(17)所需要的姿态角为θd、φd和ψd, 为了实现θ、φ和ψ对于θd、φd和ψd的跟踪, 需要对其进行求解。
由(2)和(11)式可以推出
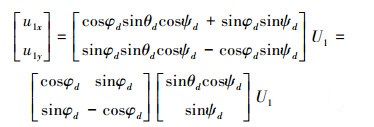
|
(19) |
由于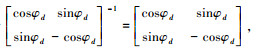
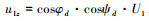
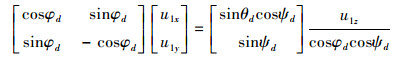
|
(20) |
由(20)的第一行可得
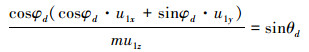
|
(21) |
需要注意的是:当(21)式左边的值超出[-1 1], 会造成θd不存在。解决办法是, 当左边的值大于1时, 令sinθd=1, 也即θd=π/2;当左边的值小于-1时, 令sinθd=-1, 也即θd=-π/2。从而可以得到θd表达式为

|
(22) |
由(20)的第二行可得
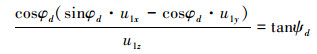
|
(23) |
从而

|
(24) |
从而得到位置控制律为
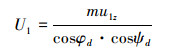
|
(25) |
由(1)式可得, 用来描述姿态的子系统为
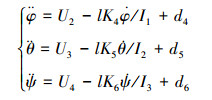
|
(26) |
针对(26)式设计的滑模函数为: 
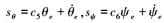
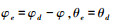
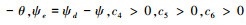
以滚转角为例, 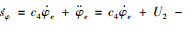
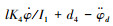
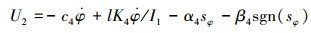
|
(27) |
式中, α4>0, β4≥D4≥0。从而, 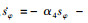
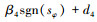
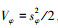
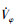
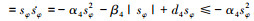
同理, 俯仰角和偏航角的滑模控制律设计如下:
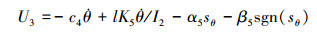
|
(28) |
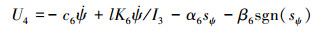
|
(29) |
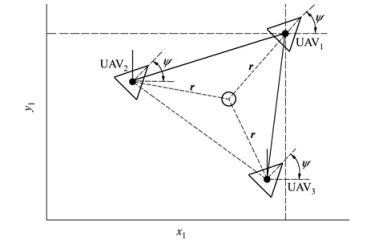
以3架四旋翼无人机构成的机组为例, 提出一种围绕半径为r的圆形成的正三角形编队, 其几何结构如图 1所示。
|
| 图 1 编队的几何结构和通信拓扑示意图 |
其中, UAV1能够接收所有的指令, 其主要任务是完成规划好的轨迹, 约定所有无人机在同一高度飞行。无人机的主要参数如表 1所示:
| 参数名 | 大小 |
| m/kg | 2 |
| l/m | 0.21 |
| Ki(i=1, 2, 3)/(kg·m-1) | 0.01 |
| Ki(i=4, 5, 6)/(kg·m-1) | 0.012 |
| Ii(i=1, 2)/(kg·m) | 1.25 |
| I3/(kg·m) | 2.5 |
| di(i=1, 2, 3)/(m·s-2) | 0.1 |
| di(i=4, 5, 6)/(rad·s-2) | 0.1 |
当无人机编队达到约定高度后, 能够在XY平面内按照期望的编队飞行。为了保持编队的形状, 每个无人机之间的距离保持恒定。由编队的几何结构, 可以得到加权邻接矩阵以及相应的拉普拉斯矩阵分别为
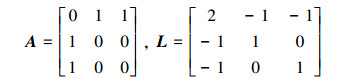
|
通过计算可以得到λ2=1, λ3=3, 令k1=k2=1, 由定理2可以得到:τ2=0.221 2, τ3=0.365 7, 从而, τ*=0.221 2, 即, 编队系统所允许的最大通信延迟为0.221 2 s, 取延时时间τ=0.2 s。3架无人机的初始位置和初始速度如表 2所示。
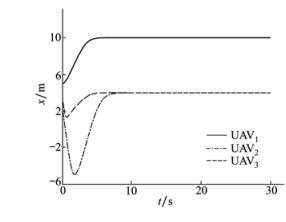
|
| 图 2 无人机编队的x轴方向的航迹 |

|
| 图 3 无人机编队在y轴方向的航迹 |
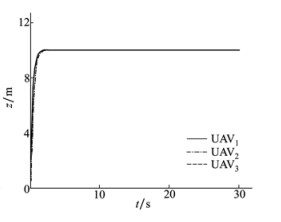
|
| 图 4 无人机编队在z轴方向的航迹 |
|
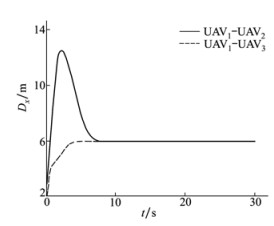
| 图 5 UAV1与UAV2、UAV3在x轴方向的距离 |
|
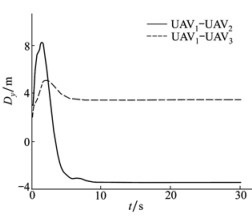
| 图 6 UAV1与UAV2、UAV3在y轴方向的距离 |
|
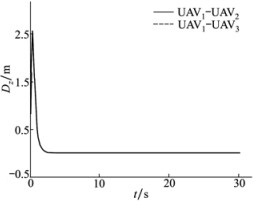
| 图 7 UAV1与UAV2、UAV3在z轴方向的距离 |
仿真中, 设置UAV1期望位置为(10, 10, 10)m, 初始速度都为0, 半径r=4 m。由图中可知, 当无人机编队在同时受到干扰和通信延时的约束时, 虽然在实现编队的初期会有一定的影响, 但会很快恢复到期望的编队。由此可以看出, 利用本文所提出的一致性编队算法和滑模控制方法, 在延时时间不超过最大允许延时时间的前提下, 3架无人机组成的编队能够达到预期的位置并保持编队队形。
5 结论本文基于无人机编队中存在通信时延的问题, 提出了相应的一致性编队算法, 给出存在时延情况下, 计算延时裕度的具体公式; 针对无人机的非线性特性和所受的干扰, 利用滑模控制算法保证了系统控制性能的基础上, 也能一定程度上解决干扰的影响。最终, 通过仿真验证了所提出控制策略的有效性。未来的工作会考虑不可知和不可建模的干扰, 以及时变通信延迟等问题。
致谢
本文工作得到陕西省飞行控制与仿真技术重点实验室的支持和资助。
| [1] | REDROVAN D V, KIM D. Multiple Quadrotors Flight Formation Control Based on Sliding Mode Control and Trajectory Tracking[C]//2018 International Conference on Electronics, Information, and Communication, 2018: 1-6 |
| [2] | GUERRERO J A, CASTILLO P, SALAZAR S, et al. Mini Rotorcraft Flight Formation Control Using Bounded Inputs[J]. Journal of Intelligent & Robotic Systems, 2012, 65(1/2/3/4): 175-186. |
| [3] |
王品, 姚佩阳. 多无人机系统分布式编队控制[J]. 计算机工程与应用, 2016, 52(16): 1-6.
WANG Pin, YAO Peiyang. Method of Distributed UAV Formation Control[J]. Computer Engineering and Applications, 2016, 52(16): 1-6. (in Chinese) DOI:10.3778/j.issn.1002-8331.1512-0236 |
| [4] |
熊涛, 曹科才, 柴运, 等. 基于输入约束一致性算法的多无人机编队控制[J]. 计算机工程与应用, 2018, 54(12): 51-56, 125.
XIONG Tao, CAO Kecai, CHAI Yun, et al. Consensus Algorithm with Input Constraint Based Formation Control for Multiple UAVs[J]. Computer Engineering and Applications, 2018, 54(12): 51-56, 125. (in Chinese) DOI:10.3778/j.issn.1002-8331.1704-0458 |
| [5] | ZHU X, YAN J, QU Y. Distributed Consensus Algorithm for Networked Euler-Lagrange Systems with Self-Delays and Uncertainties[J]. Journal of Systems Engineering and Electronics, 2012, 23(6): 898-905. DOI:10.1109/JSEE.2012.00110 |
| [6] |
王品, 姚佩阳. 存在时延的分布式无人机编队控制方法[J]. 计算机测量与控制, 2016, 24(9): 181-183.
WANG Pin, YAO Peiyang. Method of Distributed UAVs Formation with Time-Delay[J]. Computer Measurement & Control, 2016, 24(9): 181-183. (in Chinese) |
| [7] | LI S, CHEN Y, YANG Z, et al. Formation Fight Control of Multi-UAVs with Communication Delay[J]. Information and Control, 2012, 41(2): 142-146. |
| [8] | HOU W, FU M, ZHANG H, et al. Consensus Conditions for General Second-Order Multi-Agent Systems with Communication Delay[J]. Automatica, 2017, 75: 293-298. DOI:10.1016/j.automatica.2016.09.042 |
| [9] |
张汝波, 姜丽梅, 刘佰龙. 具有时延的编队控制系统稳定性分析方法[J]. 西南交通大学学报, 2011, 46(5): 770-778.
ZHANG Rubo, JIANG Limei, LIU Bailong. Review of Stability Analyses of Formation Control with Time Delay[J]. Journal of Southwest Jiaotong University, 2011, 46(5): 770-778. (in Chinese) DOI:10.3969/j.issn.0258-2724.2011.05.010 |
| [10] | ABDESSAMEUD A, TAYEBI A. Formation Stabilization of VTOL UAVs Subject to Communication Delays[C]//49th IEEE Conference on Decision and Control, 2010: 4547-4552 |
| [11] | SHANG Y. Average Consensus in Multi-Agent Systems with Uncertain Topologies and Multiple Time-Varying Delays[J]. Linear Algebra and its Applications, 2014, 459: 411-429. DOI:10.1016/j.laa.2014.07.019 |
| [12] | SUN Y G, WANG L, XIE G. Average Consensus in Networks of Dynamic Agents with Switching Topologies and Multiple Time-Varying Delays[J]. Systems & Control Letters, 2008, 57(2): 175-183. |
| [13] | QIN J, GAO H, ZHENG W X. Second-Order Consensus for Multi-Agent Systems with Switching Topology and Communication Delay[J]. Systems & Control Letters, 2011, 60(6): 390-397. |
| [14] | GRANCHAROVA A, GRØTLI E I, HO D T, et al. UAVs Trajectory Planning by Distributed MPC under Radio Communication Path Loss Constraints[J]. Journal of Intelligent & Robotic Systems, 2015, 79(1): 115-134. |
| [15] | XU R, ÖZGVNER V. Sliding Mode Control of a Class of Underactuated Systems[J]. Automatica, 2008, 44(1): 233-241. DOI:10.1016/j.automatica.2007.05.014 |
| [16] | HOU W, FU M, ZHANG H, et al. Consensus Conditions for General Second-Order Multi-Agent Systems with Communication Delay[J]. Automatica, 2017, 75: 293-298. DOI:10.1016/j.automatica.2016.09.042 |
| [17] |
刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2012.
LIU Jinkun. Sliding Mode Variable Structure Control and MATLAB Simulation[M]. Beijing: Tsinghua University Press, 2012. (in Chinese) |



