飞行器设计中一个永恒的主题是减阻。已有研究表明,摩擦阻力在典型亚声速民机巡航状态下占总阻力的比例可以高达50%[1],减小摩擦阻力对改善民机性能、降低民机运营成本有重要意义。飞行条件下,湍流边界层大比例占据飞行器机翼、机身的表面,同时,湍流边界层摩擦阻力大约是层流的10倍,所以,湍流边界层减阻对飞行器设计有着十分重要的意义。
在湍流边界层研究中,壁面摩擦应力τw是非常关键的一个物理量,它可以用来计算摩擦阻力、判断流动转捩位置等。一直以来,研究人员致力于更简便、准确地测量得到壁面摩擦应力。常用的壁面摩擦应力测量方法主要包括普雷斯顿管法、油膜干涉法、底层隔板法、表面热膜法等[2-5]。随着微机电系统的发展,壁面剪应力微传感器引起了研究人员的重视,也得到了越来越多的应用[6-8]。然而这些方法会不同程度破坏固壁表面,影响测量的准确性。
利用热线风速仪测量湍流场也是获得壁面摩擦应力的有效方法[9-11]。热线风速仪是一种能准确测量流体运动的仪器,它可以利用热线探针在单点进行高精度、高响应频率的速度测量。以美国TSI公司的IFA-300型恒温热线风速仪为例,其采用超低噪声电路,拥有高空间分辨率和几百干赫兹的高频时间响应,单点精确测量速度范围可从每秒1厘米至数百米,非常适合于湍流测量。利用热线风速仪,辅以高精度移测架系统,可以实现湍流边界层时均速度型的精确测量,同时,热线探针不需要接触固体壁面,不会对壁面摩擦应力产生影响。
壁面摩擦应力与壁面摩擦速度的关系式为τw=ρuτ2, 用热线风速仪测量湍流场以获得壁面摩擦应力, 可以归结为求解壁面摩擦速度uτ。具体来讲, 对于热线风速仪测量得到的湍流边界层空间点时均速度序列(y, u), 可以通过壁面摩擦速度uτ无量纲化为(y+, u+), 其中y是所测空间点距壁面的物理高度, y+是无量纲的壁面单位, u+是无量纲时均速度, y+和u+的具体定义见2.1节。然后, 根据湍流边界层的无量纲时均速度分布规律反推壁面摩擦速度uτ的大小。
湍流边界层由里到外通常分为黏性底层、缓冲层、对数区、尾流区。黏性底层、缓冲层和对数区常统称为内区。
黏性底层的范围大约是y+≤(5~10), 无量纲速度分布规律为u+=y+。黏性底层里壁面摩擦应力τw主要为黏性切应力, 即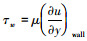
黏性底层向上是缓冲层, 其范围是(5~10) < y+ < (30~70), 该层目前没有公认的无量纲速度分布公式。缓冲层里湍流切应力显著增加, 在这一区域内黏性切应力与湍流切应力的作用都不能忽略。
缓冲层之上是对数区, 理论范围是(30~70)≤y+, y/δ≤0.2, 对数区里无量纲速度分布规律为u+=1/κ·ln(y+)+B, 式中κ和B均为常数, 此区域里湍流切应力占据主导地位。
黏性底层和对数区的无量纲时均速度分布规律非常明确, 研究人员常利用这2个区域的空间点时均速度序列(y, u)来反推摩擦速度uτ, 但是, 也存在各自的问题。对黏性底层而言, 它的厚度非常薄, 加之热线探针太靠近壁面时会产生所谓的“壁面效应”(wall effect[9]), 所以在黏性底层里很难测得足够的空间点速度, 因而不容易由速度分布规律确定壁面摩擦速度uτ。对对数区而言, 通常认为近壁区域湍流切应力为常数, 且等于壁面摩擦应力, 也即当地摩擦速度与壁面摩擦速度相等, 从而可以根据u+=1/κ·ln(y+)+B拟合求解壁面摩擦速度uτ。常用的求解壁面摩擦速度uτ的Clauser方法[12]是将实验测量的对数区时均速度序列(y, u)拟合到(y+, u+), 从而得到uτ。由于仅仅使用对数区的测点数据进行拟合, 且事实上近壁区湍流切应力不为常数, 它与壁面摩擦应力存在差值, 所以Clauser方法求得的uτ往往会比真实值偏大, 文献[13]报道平均误差在8% ~ 20%。
湍流边界层存在许多无量纲速度型模型, 例如White Law[14]、Spalding[15]速度型、Musker[16]速度型等, 它们给出了从黏性底层、缓冲层直至对数区的速度分布规律。潘光、胡海豹等[17-18]研究了Spalding速度型公式用于光滑表面和脊状表面湍流时均速度型的最小二乘拟合, 认为在这种拟合结果中摩擦速度的精度可以得到保证。王康俊等[19]以油膜干涉法测得的壁面摩擦应力为基准, 对比研究了黏性底层拟合、对数律区拟合以及Spalding速度型公式拟合各自求得的壁面摩擦速度的差异, 结果表明Spalding速度型公式拟合的准确性和可靠性更优。Kendall等[20]分别以Spalding速度型公式和Musker速度型公式为基础, 研究了如何通过拟合方法求解壁面摩擦速度, 平均误差只有大约0.5%。针对Clauser方法仅仅使用对数区的测点数据进行拟合的缺点, 本文以无量纲速度型模型White Law为目标曲线, 以实验中利用热线风速仪测得的缓冲层及对数区的测点速度为拟合数据, 通过非线性拟合, 得到壁面摩擦速度uτ。这种改进的方法可以很大程度提高uτ的求解精度, 从而也提高了壁面摩擦应力τw的精度。
1 实验设置 1.1 风洞本文的实验是在一座小型下吹式低速风洞里进行的, 风洞的实物图如图 1所示。

|
| 图 1 小型下吹式低速风洞实物图 |
风洞运行由一部变频电机控制, 电机工作频率10~50 Hz, 电机带动风机转动, 将空气吸入风洞, 经静流段、阻尼段、收缩段到达实验段。静流段、阻尼段、收缩段平直部分的总长为1 366 mm, 收缩段收缩部分的长度为770 mm。从收缩段出口至风洞出口, 该部分总长4 500 mm, 其横截面为720 mm(宽)×200 mm(高)的矩形。核心实验区距收缩段出口2 000 mm, 左右侧壁以及下壁是有机玻璃板, 上壁为钢板, 安装了一套三维移测架, 钢板上开有矩形测量窗口(675 mm(流向)×220 mm(展向)), 以供热线探杆由上至下伸入风洞并能够随移测架自由移动。风洞稳定风速为7~20 m/s, 风速控制精度0.1 m/s, 稳定风速下的风洞背景湍流度不超过5‰。
1.2 实验方案实验来流风速为U∞=15.4 m/s, 为了获得充分发展的湍流边界层, 在收缩段出口下游120 mm的风洞下壁板处布置了一根直径4 mm的绊线, 绊线下游25 mm位置黏贴了一张宽度为50 mm的120目砂纸。距砂纸尾缘1 820 mm处是一个可替换合成射流模块, 模块长宽均为100 mm。本文主要是介绍一种利用非线性拟合求解湍流边界层壁面摩擦速度的方法, 所以本文的实验是在没有合成射流的情况下进行的, 此时采用一块无开孔的盖板替换有开孔的合成射流盖板, 以避免几何外形的不连续对边界层流动产生影响。
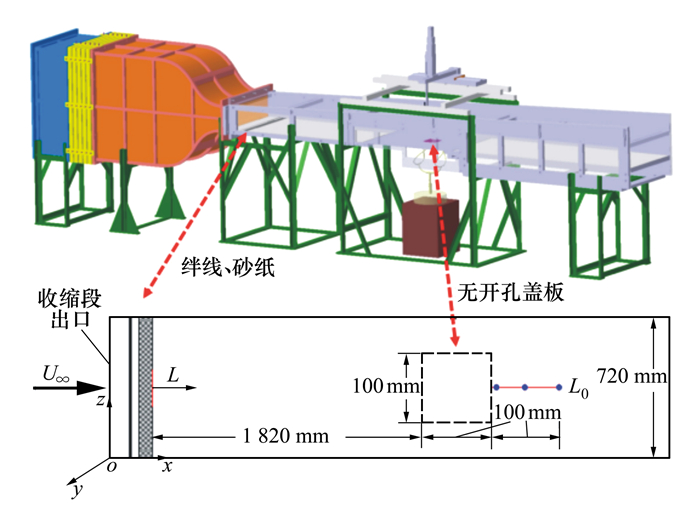
采用美国TSI公司的IFA-300型恒温热线风速仪和TSI-1218-20型标准边界层探针测量了无开孔盖板下游10, 50, 100 mm流向站位的速度型, 如图 2中L0线上3个标记点所示, 3个站位距砂纸尾缘的距离分别是L=1 930 mm, 1 970 mm, 2 020 mm。在进行速度型测量时, 利用步进精度为0.01 mm的三维移测架沿壁面法向(y轴)由近至远移动热线探针, 共测量了法向高度上140个空间点的速度分布, 其中第1~17点探针移动间隔为0.05 mm, 第18~29点探针移动间隔为0.1 mm, 第30~47点探针移动间隔为0.2 mm, 第48~125点探针移动间隔为0.5 mm, 第126~140点探针移动间隔为1 mm。测量的最低点(第1点)距壁面名义高度为0.4 mm, 最高点(第140点)距壁面名义高度为60 mm。边界层内保证不少于120个测点。热线采样频率20 kHz, 采样时长6.553 55 s, 采样点数共131 072。
|
| 图 2 实验模型与测量站位示意图(非等比例) |
实验中利用热线风速仪测量得到的空间点时均速度序列(y, u)可以通过壁面摩擦速度uτ无量纲化为(y+, u+), 其中y是所测空间点距壁面的物理高度, y+是无量纲的壁面单位, u+是无量纲时均速度。y+和u+的定义如下

|
(1) |
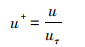
|
(2) |
式中:ν是流体的运动黏性系数;y0表示壁面坐标理论零点位置, 用于修正实验测量时测点的真实高度。
White Law[14]是湍流边界层的壁面积分律, 它以积分的形式给出了无量纲时均速度u+与无量纲壁面单位y+的关系, 其具体表达式为
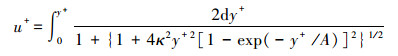
|
(3) |
式中, κ=0.41是von Karman常数, A=25。
将实验测得的无量纲时均速度序列(y+, u+)拟合到White Law曲线, 在拟合残差最小时即可以得到壁面坐标理论零点位置y0和壁面摩擦速度uτ。
2.2 残差函数依据最小二乘原理, 定义残差函数为
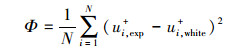
|
(4) |
式中:ui, exp+是实验测得的无量纲时均速度, 其对应的无量纲壁面单位是yi, exp+;ui, white+是White Law壁面积分律在yi, exp+处的无量纲速度。
Kendall等人[20]在他们的研究工作中发现, 采用公式(4)作为残差函数, 拟合得到的无量纲时均速度型曲线并非最好, 建议采用“残差绝对值的相对变化量之和”作为残差函数来控制拟合结果, 定义为
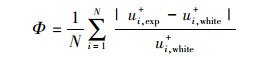
|
(5) |
一般来讲, 壁面坐标理论零点位置在最低测点之下, 即y0 < y1, 但是如果在实验过程中对y1标定不准确, 使得y1比真实值偏低, 以至出现y0>y1的情况, 根据公式(1)、(3)、(5), 此时会导致y+ < 0, u+ < 0, Φ < 0, 那么在搜索Φ的最小值并提取对应的y0和uτ时将可能获得错误的结果。为了避免这种情况, 本文对公式(5)进行了改进, 并作为本文采用的残差函数, 如公式(6)所示
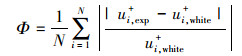
|
(6) |
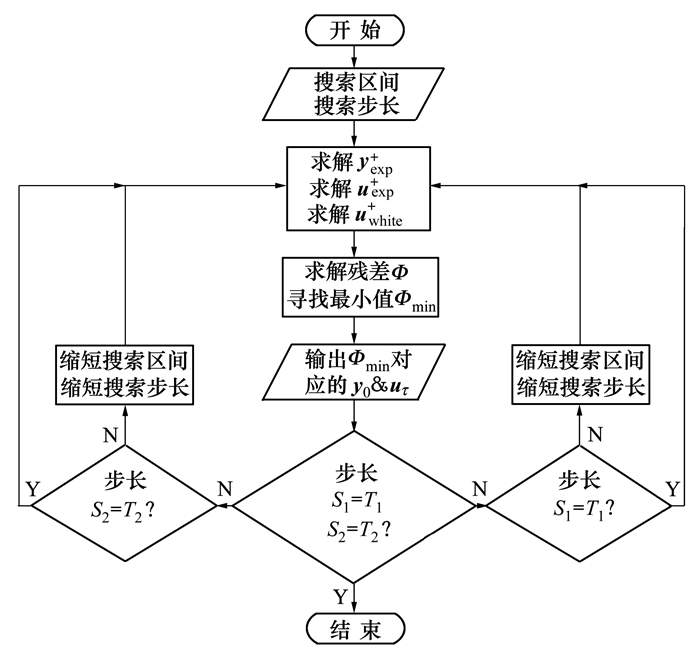
以2.1节中公式(3)给出的White Law为目标曲线, 以2.2节中公式(6)为残差函数, 编制了关于双参数y0和uτ的非线性曲线拟合MATLAB程序, 流程图如图 3所示, 图中S1和S2分别表示y0和uτ的搜索步长, T1和T2分别表示y0和uτ的误差限。
|
| 图 3 双参数非线性拟合MATLAB程序流程图 |
程序运行需事先给定初始搜索区间和搜索步长, 运行过程中则需要根据每一轮搜索获得的当前最优解来确定新的搜索区间和搜索步长。本文的MATLAB程序根据y0和uτ分别落在各自搜索区间中的具体位置, 采用类似二分法的思路缩短搜索区间长度:
·若落在前1/4个搜索区间, 则:搜索区间下限不变, 上限以y0(或uτ)的当前最优解为起始外扩1/4原搜索区间的长度;
·若落在后1/4个搜索区间, 则:搜索区间上限不变, 下限以y0(或uτ)的当前最优解为起始外扩1/4原搜索区间的长度;
·若落在中间1/2个搜索区间, 则:以y0(或uτ)的当前最优解为中心, 搜索区间减半。
本文的MATLAB程序缩短搜索步长的方法是:新一轮的搜索步长缩短至上一轮的1/10。
3 实验结果和讨论本文测量了距砂纸尾缘L=1 930, 1 970, 2 020 mm流向站位的速度型, 在每个站位处沿法向均有140个测点, 边界层内测点数不少于120个。本节将以L=1 930 mm站位的测量结果为例, 讨论初值选取、拟合数据范围对双参数非线性拟合结果的影响, 并在最后给出具体的实验结果。
3.1 初值选取对拟合结果的影响在运行程序之前, 需要先给定y0和uτ的初始搜索区间和搜索步长。有2种给定初始搜索区间的方法。第一种方法, 对y0而言, 可以以最低测点的物理坐标y1为搜索区间的上限; 对uτ而言, 可以利用光滑平板湍流边界层的理论公式预估uτ的大小, 然后以预估值为中心给定一个合适长度的搜索区间。另一种方法是对y0和uτ都直接给定较大的初始搜索区间。2种方法的差别主要体现在程序运行时间的不同, 一般情况下, 初始搜索区间越大, 程序运行用时越长。初始搜索步长应根据具体实验具体确定, 本文选取y0的初始搜索步长为0.1 mm, 误差限为0.001 mm; uτ的初始搜索步长为0.01 m/s, 误差限为0.000 1 m/s。
表 1给出了L=1 930 mm站位所测实验数据通过非线性曲线拟合得到的y0和uτ数值。由表 1可以发现, 取不同长度的搜索区间时, 程序经过一次搜索, 都能够收敛到当前的最优y0和uτ组合, 随着搜索区间和搜索步长的缩短, 最小拟合残差Φmin减小, 拟合结果的精度进一步提高, 最终拟合得到6组数据, y0的标准差为σ(y0)=0.000 27 mm, uτ的标准差为σ(uτ)=0.000 091 m/s, 说明程序拟合结果稳定性非常好, 受给定的初始搜索区间的影响很小, 只要给定的初始搜索区间包含物理解, 则程序拟合结果对初始搜索区间并不敏感。
| 初始搜索区间 | 第一轮搜索拟合结果 | 最终拟合结果 | ||||||
| y0/(mm~mm) | uτ/(m/s~m/s) | Φmin | y0/mm | uτ/(m·s-1) | Φmin | y0/mm | uτ/(m·s-1) | |
| y0:0.0~0.8 | uτ:0.2~1.0 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 283 | y0=0.398 5 | uτ=0.638 40 | |
| y0:0.1~0.7 | uτ:0.3~0.9 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 287 | y0=0.398 4 | uτ=0.638 28 | |
| y0:0.2~0.6 | uτ:0.4~0.8 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 291 | y0=0.398 3 | uτ=0.638 35 | |
| y0:0.3~0.5 | uτ:0.5~0.7 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 295 | y0=0.398 1 | uτ=0.638 32 | |
| y0:0.3~0.4 | uτ:0.6~0.7 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 281 | y0=0.398 8 | uτ=0.638 54 | |
| y0:0.3~0.5 | uτ:0.6~0.7 | 0.003 896 | y0=0.40 | uτ=0.640 | 0.003 296 | y0=0.398 1 | uτ=0.638 34 | |
在特定流向站位完成速度型测量后, 并不是所有的测点数据都可以用来进行无量纲速度型曲线拟合, 为了保证拟合精度, 需要合理选择拟合数据范围。本小节将采用不同范围的数据进行拟合, 通过对比, 说明正确地选择拟合数据范围的重要性。
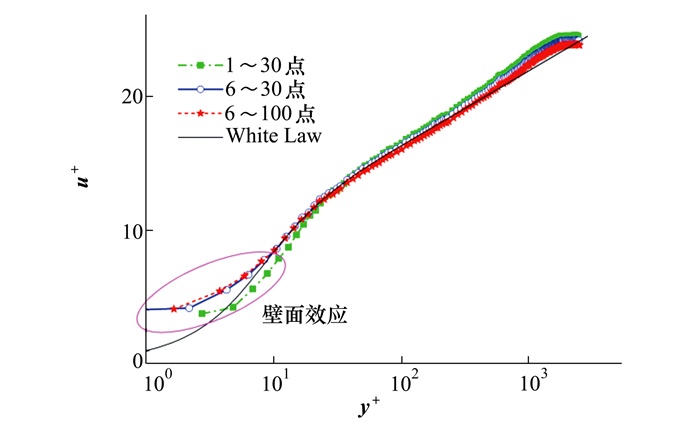
为了考察不同拟合数据范围对拟合结果的影响, 根据表 1选定y0初始搜索区间为0.3~0.5 mm、uτ的初始搜索区间为0.6~0.7 m/s进行拟合作业。表 2给出了据此得到的L=1 930 mm站位最终拟合结果。图 4展示了利用数据范围1~30点、6~30点和6~100点进行拟合作业得到的y0和uτ绘制的无量纲速度型曲线。
| 拟合数据范围 | Φmin | y0/mm | uτ/(m·s-1) |
| 1~30点 | 0.040 616 | 0.333 5 | 0.629 55 |
| 1~40点 | 0.032 886 | 0.337 5 | 0.632 61 |
| 6~30点 | 0.003 956 | 0.399 1 | 0.638 74 |
| 6~40点 | 0.003 296 | 0.398 1 | 0.638 34 |
| 6~50点 | 0.003 426 | 0.399 1 | 0.638 74 |
| 6~60点 | 0.005 073 | 0.402 1 | 0.640 54 |
| 6~80点 | 0.009 531 | 0.404 1 | 0.642 54 |
| 6~100点 | 0.013 247 | 0.411 1 | 0.647 56 |
由图 4可见, 利用1~30点进行拟合作业时, 拟合速度型曲线与White Law在缓冲层底部未能完整贴合, 两者在黏性底层的差异更为明显, 尤其是第1点发生了明显的转折上扬, 这种现象往往都是由“壁面效应”导致的。在剔除存在“壁面效应”的测点(1~5点)、将拟合数据范围选为6~30点后, 拟合速度型曲线与White Law在缓冲层吻合良好, 改用6~100点也体现出比1~30点更好的拟合效果。
|
| 图 4 L=1 930 mm站位采用不同拟合数据范围进行拟合作业获得的拟合结果 |
“壁面效应”对拟合结果的影响是巨大的, 因其本身即是测量中产生的坏点, 如表 2中数据范围为1~30点和1~40点所示, 拟合得到的y0和uτ与其他数据范围的结果相比有明显偏差, 最小拟合残差甚至比其他情形大一个量级。对于这些异常点, 在选取拟合数据时应当舍弃。
从第50测点开始进入尾流区, 选取的拟合数据中有若干数据点落在尾流区, 则会导致uτ的拟合值偏大, 如表 2中6~60点、6~80点、6~100点的拟合结果所示。uτ偏大的原因在于, 湍流边界层从对数区过渡到尾流区, 速度型曲线向上产生一定程度的偏折, 使得尾流区的速度型曲线比对数区偏上, 若拟合数据范围包含尾流区, 根据最小二乘原理, 要保证拟合数据点离目标曲线的“距离”尽量小, 最小拟合残差必然是在一种中间状态下获得,即在对数区, 拟合速度型曲线(实验)在目标速度型曲线(理论模型)之下; 在尾流区拟合速度型曲线在目标速度型曲线之上。
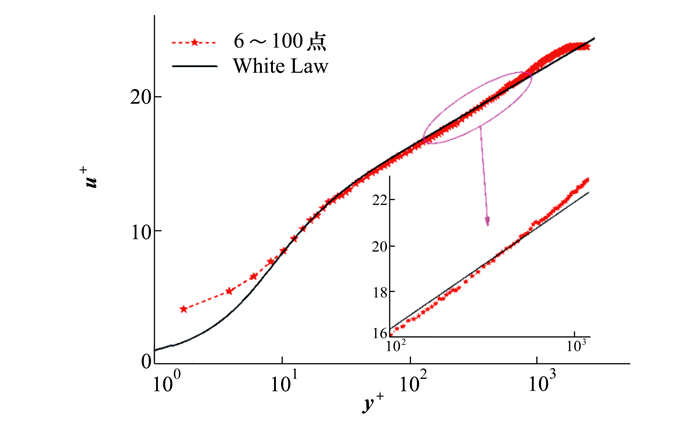
图 5以拟合数据范围6~100点为例, 清晰地展示了上述情形, 其效果相当于拟合速度型曲线整体向下“平移”, 根据公式(2), uτ的拟合值将比真实值偏大, 并且拟合数据包含的尾流区测点越多, uτ的拟合值越偏大。所以, 在确定拟合数据范围时应保证最高点没有落在尾流区中, 为稳妥计, 可以将最高点选取适当下移, 而并不一定要将对数区所有测点都纳入拟合数据中。
|
| 图 5 L=1 930 mm站位拟合数据包含尾流区测点导致拟合速度型曲线向下“平移” |
实际应用中, 作者选取拟合数据范围的经验是:第一步, 根据理论公式预估的uτ值计算各个测点对应的y+(计算时取y0=0);第二步, 根据y+的计算结果选取对数区及以下的所有测点作为拟合数据范围进行第一次拟合; 第三步, 观察拟合结果, 调整拟合数据的最低点和最高点, 具体做法是:只要没有“壁面效应”, 则测量数据的最低点即可作为拟合数据的最低点, 同时, 要保证最高点不在尾流区中; 第四步, 在最高点不在尾流区的前提下, 上下调整最高点位置, 进行多次拟合, 选取Φmin最小的一次拟合作为最终拟合结果。
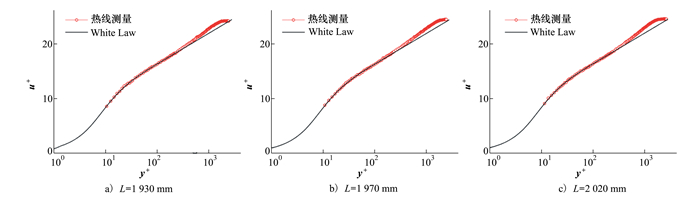
3.3 实验结果根据3.1与3.2节的讨论, 通过合理选取拟合数据范围, 分别对L=1 930, 1 970, 2 020 mm流向站位的实验数据进行双参数非线性拟合处理, 结果如表 3所示, 并利用拟合所得y0和uτ绘制了3个站位的无量纲速度型曲线, 如图 6所示。光滑平板湍流边界层的形状因子H定义为边界层位移厚度与动量厚度之比, 其理论值为H ≈1.3[21], 由表 3可见, 3个站位的边界层形状因子均与理论数值接近, 说明所测站位处湍流边界层已经充分发展, 反映在图 6中, 实验测得的速度型在缓冲层和对数区均与White Law吻合得非常好。这也说明了本文求得的壁面摩擦速度uτ数值准确, 求解方法可靠。
| 站位 | 拟合数据范围 | y0/mm | uτ/(m·s-1) | τw/(N·m-2) | δθ/mm | Reθ | H |
| L=1 930 mm | 6~40点 | 0.398 1 | 0.638 34 | 0.475 6 | 3.69 | 3 759 | 1.291 |
| L=1 970 mm | 7~36点 | 0.291 0 | 0.631 71 | 0.465 8 | 3.92 | 3 995 | 1.280 |
| L=2 020 mm | 3~41点 | 0.223 3 | 0.630 31 | 0.463 7 | 3.96 | 4 033 | 1.294 |
|
| 图 6 L=1 930, 1 970, 2 020 mm站位的无量纲速度型(未显示有“壁面效应”的测点) |
作为湍流测量的基本手段, 热线风速仪现今依然广泛应用于湍流研究。本文用恒温热线风速仪测量了湍流边界层3个流向站位的时均速度型, 编制了关于壁面坐标理论零点位置y0和壁面摩擦速度uτ的双参数非线性曲线拟合MATLAB程序, 并以所测实验数据为基础讨论了初始搜索区间和搜索步长以及拟合数据范围对拟合结果的影响。本文得到的主要结论有:
1) 本文的MATLAB程序拟合结果稳定性非常好, 只要给定的初始搜索区间包含物理解, 则程序拟合结果对初始搜索区间并不敏感;
2) 初始搜索步长应根据具体实验具体确定;
3) 在选取拟合数据范围时, 应保证最高点不在尾流区中, 只要没有发生“壁面效应”, 最低点可以一直下探到缓冲层甚至更低, 而不用局限在对数区, 这扩大了可用拟合数据的范围, 提高了uτ的求解精度。
本文采用了湍流边界层壁面积分律White Law作为无量纲速度型模型, 事实上, 将White Law替换成Spalding速度型、Musker速度型等, 同样可以求解壁面摩擦速度uτ。以不同的无量纲速度型模型为目标曲线, 对同一站位的实验数据分别进行双参数非线性拟合, 这样将会得到一组uτ, 从而可以给出uτ的置信区间。
| [1] | THIBERT J J, RENEAUX J, SCHMITT V. ONERA Activities on Drag Reduction[C]//Proceedings of the Seventeenth Congress of the International Council of the Aeronautical Sciences, 1990: 1053-1064 |
| [2] | WINTER K G. An Outline of the Techniques Available for the Measurement of Skin Friction in Turbulent Boundary Layers[J]. Progress in Aerospace Sciences, 1979, 18(77): 1-57. |
| [3] | NITSCHE W, HABERLAND C, THUENKER R. Comparative Investigations on Friction Drag Measuring Techniques in Experimental Aerodynamics[C]//Proceedings of the Fourteenth Congress of the International Council of the Aeronautical Sciences, 1984: 391-403 |
| [4] | FERNHOLZ H H, JANKE G, SCHOBER M, et al. New Developments and Applications of Skin-Friction Measuring Techniques[J]. Measurement Science & Technology, 1996, 7(10): 1396. |
| [5] | ZANOUN E S, JEHRING L, EGBERS C. Three Measuring Techniques for Assessing the Mean Wall Skin Friction in Wall-Bounded Flows[J]. Thermophysics & Aeromechanics, 2014, 21(2): 179-190. |
| [6] | PAPEN T V, STEFFES H, NGO H D, et al. A Micro Surface Fence Probe for the Application in Flow Reversal Areas[J]. Sensors and Actuators A(Physical), 2002, 97/98: 264-270. DOI:10.1016/S0924-4247(01)00873-1 |
| [7] | SAVELSBERG R, SCHIFFER M, OBERMEIER E, et al. Calibration and Use of a Surface Fence for Wall Shear Stress Measurements in Turbulent Flows[J]. Anaesthesia & Intensive Care Medicine, 2012, 13(3): 77-80. |
| [8] |
严宇超, 姜澄宇, 马炳和, 等. 壁面剪应力标定方法研究综述[J]. 实验流体力学, 2017, 31(2): 20-25.
YAN Yuchao, JIANG Chengyu, MA Binghe, et al. Review of the Calibration Methods and Devices for Wall Shear Stress[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(2): 20-25. (in Chinese) |
| [9] | HUTCHINS N, CHOI K S. Accurate Measurements of Local Skin Friction Coefficient Using Hot-Wire Anemometry[J]. Progress in Aerospace Sciences, 2002, 38(4): 421-446. |
| [10] | ZAFIRYADIS F, MEYER K E, ERGIN F G. Measurement of Turbulent Skin Friction Drag Coefficients Produced by Distributed Surface Roughness of Pristine Marine Coatings[C]//Tenth International Symposium on Turbulence and Shear Flow Phenomena, 2017 |
| [11] | BOIKO A V, KORNILOV V I. Hot-Wire Anemometer Measurement of Local Skin Friction Coefficient[J]. Thermophysics and Aeromechanics, 2010, 17(4): 577-586. DOI:10.1134/S0869864310040104 |
| [12] | CLAUSER F H. The Turbulent Boundary Layer[J]. Advances in Applied Mechanics, 1956, 4(3): 1-51. |
| [13] | BLACKWELDER R F, HARITONIDIS J H. Scaling of the Bursting Frequency in Turbulent Boundary Layers[J]. Journal of Fluid Mechanics, 1983, 132(132): 87-103. |
| [14] | WHITE F M. Viscous Fluid Flow[M]. Third Edition. New York: McGraw-Hill, 2006. |
| [15] | SPALDING D B. A Single Formula for the "Law of the Wall"[J]. Journal of Applied Mechanics, 1961, 28(3): 455. DOI:10.1115/1.3641728 |
| [16] | MUSKER A J. Explicit Expression for the Smooth Wall Velocity Distribution in a Turbulent Boundary Layer[J]. AIAA Journal, 1979, 17(6): 655-657. DOI:10.2514/3.61193 |
| [17] |
潘光, 黄明明, 胡海豹, 等. Spalding公式在脊状表面湍壁摩擦力测量中的应用[J]. 力学学报, 2009, 41(1): 15-20.
PAN Guang, HUANG Mingming, HU Haibao, et al. Application of Spalding Formula in Wall Friction Stress Measurement on Riblet Surface[J]. Chineses Journal of Theoretical and Applied Mechanics, 2009, 41(1): 15-20. (in Chinese) DOI:10.3321/j.issn:0459-1879.2009.01.003 |
| [18] |
胡海豹, 宋保维, 刘占一, 等. 基于湍流边界层时均速度分布的脊状表面减阻规律研究[J]. 航空动力学报, 2009, 24(5): 1040-1047.
HU Haibao, SONG Baowei, LIU Zhanyi, et al. Research about the Characteristic of Drag Reduction Over Riblets Surface Based on Average Velocity Profile in the Turbulent Boundary Layer[J]. Journal of Aerospace Power, 2009, 24(5): 1040-1047. (in Chinese) |
| [19] |
王康俊, 白建侠, 唐湛棋, 等. 用平均速度剖面法测量湍流边界层壁面摩擦速度的对比研究[J]. 实验力学, 2019, 34(2): 209-216.
WANG Kangjun, BAI Jianxia, TANG Zhanqi, et al. Comparative Study of Turbulent Boundary Layer Wall Friction Velocity Measured by Average Velocity Profile Method[J]. Journal of Experimental Mechanics, 2019, 34(2): 209-216. (in Chinese) |
| [20] | KENDALL A, Koochesfahani M. A Method for Estimating Wall Friction in Turbulent Wall-Bounded Flows[J]. Experiments in Fluids, 2008, 44(5): 773-78. DOI:10.1007/s00348-007-0433-9 |
| [21] | POPE S B. Turbulent Flows[M]. Cambridge: Cambridge University Press, 2000. |


