随着导航和自控技术的发展, 无人机的用途日益多样化。军事领域中它执行反雷达监控、侦察突袭等任务, 成为空战制胜的关键武器; 民用领域中除了进行电力巡检、农药喷洒外, 它还用于“最后一公里”物流的运输; 科研领域中可利用它获取数据进行地理测绘等。在三大应用领域中, 无人机路径规划是需要解决的核心问题。
路径规划是要求无人机在满足特定约束条件下, 寻找从初始点到目标点满足性能指标的最优飞行路径[1]。对无人机而言, 能否安全高效地躲避障碍物是提高无人机利用率的关键。因此当前首要的目标是提出并设计一种无人机在障碍物环境下避障的路径规划算法。
无人机路径规划算法目前研究得已较深入[2-4], 如粒子群算法、蚁群算法、A*算法等。但大多数学者假设障碍物是规则的[5-9], 如圆形、矩形。丁家如等将战场中威胁区域等效为圆并对规划区域进行预规划, 利用改进人工势场法获得平滑的可飞路径[5]。Turker等为研究无人机雷达规避, 将雷达等效为圆形禁飞区, 并基于二维平面采用模拟退火算法实现了路径规划[6]。Yao等虽针对路径规划提出自适应蚁狮优化算法并验证了该算法的有效性, 但仅将障碍物等效为圆形禁飞区和矩形禁飞区2种简化模型, 对障碍物边界处理较为理想化[7]。以上文献中对环境的假设造成规划空间过于理想, 与实际不符。考虑到现实环境中障碍物多为不规则形状且往往将无人机视作质点处理, 直接采用上述方法易于显著扩大障碍物所涵盖范围继而影响规划结果, 因此有待改进。近年有学者开始研究不规则环境下的路径规划[8-11]。吴海彬等运用Voronoi图理论重构环境, 将原有不规则障碍物等效为若干个圆的组合[8]。谢春生等采用Graham法将非凸多边形危险区扩展为凸多边形[9]。Xu等将障碍物扩展成圆形禁飞区并基于Laguerre图优化了规划的路径[10]。贾春雪等提出利用自动识别凸形化方式对障碍物进行规则化处理, 以此为基础规划最优路径[11]。
针对现有算法无法对不规则环境下路径进行规划的缺陷, 本文主要研究面向多类型不规则障碍物的路径规划技术。本文设计了一种基于不规则障碍物避碰检测(IOCAD)的无人机路径规划算法, 将路径规划分为障碍物预处理和多边形障碍物避撞检测两部分。首先采用栅格法对规划空域进行建模, 结合栅格划分结果对障碍物进行综合预处理, 包括基于粗糙集的弧形障碍物多边形化处理、凹多边形凸化填充处理、安全裕度处理; 其次结合平面几何知识, 在处理后的障碍物环境下利用射线法选出环境中可飞路径点, 并对多边形障碍物和路径段进行相交检测和距离检测等; 最后进行基于不规则障碍物避碰检测的无人机路径规划算法的仿真, 验证了本文算法的有效性, 同时分析出最合适的栅格粒度大小和安全裕度值。
1 环境建模及障碍物预处理 1.1 栅格法规划空域建模无人机巡航时在垂直方向不发生高度变化, 此阶段无人机在三维空间的运动可简单看做二维平面的运动。
假设无人机路径规划如下条件已知:①起始点、目的点位置; ②无人机物理性能约束(如最大转弯角、最小飞行步长); ③不规则障碍物信息; ④无人机定高巡航且可视作质点; ⑤无人机速度恒定。
将起点和终点连线作为矩形对角线, 该矩形即二维路径规划空域。以起点为原点, 矩形长边做x轴、宽边做y轴建立直角坐标系。结合物理性能约束参数、不规则障碍物等信息可确定栅格粒度的大小Ngrid。则规划空域可划分为u×v个栅格, 将栅格顶点作为待选的飞行路径点。u, v的计算式如(1)~(2)式
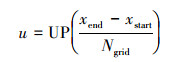
|
(1) |
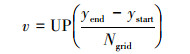
|
(2) |
式中:(xend, yend)为目的点坐标; (xstart, ystart)为起始点坐标; UP()为自定义函数, 定义为
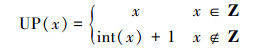
|
(3) |
式中:int(x)为取整函数;Z为整数集合。
本文采用直角坐标法标识栅格位置, 栅格中任意点的坐标同栅格坐标。图 1为栅格标识示意图。

|
| 图 1 直角坐标法标识栅格 |
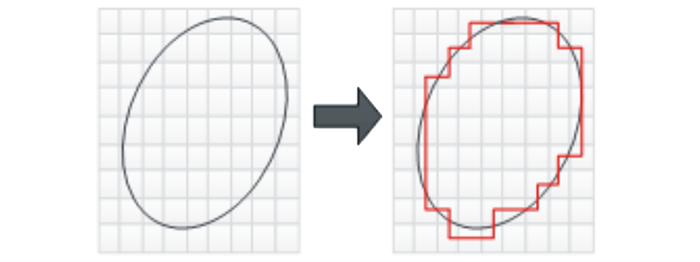
借鉴粗糙集思想对弧形障碍物多边形化处理。其方法是:确定弧形障碍物外围包线所在栅格及其定位点并按顺时针依次连接定位点, 所得多边形即为障碍物多边形化处理的结果。图 2为弧形障碍物转化为多边形障碍物的结果, 具体步骤如下。
|
| 图 2 弧形障碍物多边形化处理示意图 |
Step1 确定弧形障碍物S的外围包线L并据此包线确定各段包线li所在栅格, 称这些栅格为标记栅格并记作gi, 称标记栅格的中心点为定位点并记作ei, 其中i为外围包线的段数;
Step2 确定外围包线标记栅格中纵坐标最大的栅格(若个数大于2, 则选取横坐标小的栅格)并记此栅格坐标为g1(x1, y1), 称此栅格为主标记栅格, 依次确定其他标记栅格的坐标, 分别记作g2(x2, y2), …, gn(xn, yn), 其中n为L所占栅格的个数;
Step3 从主标记栅格开始依顺时针次序连接栅格g1, g2, …, gn, g1的定位点e1, e2, …, en, e1, 多边形e1e2…ene1即障碍物S的多边形化结果, S≈e1, e2…ene1。
1.3 凹多边形障碍物凸化填充处理定义1 简单多边形 在二维栅格中可确定多边形各顶点的坐标, 从主标记栅格开始按顺时针方向记各顶点为p1, p2, …, pm, 其中m为顶点个数。任选2条边pipi+1和pjpj+1, 若满足以下任一条件:①此两边不相交; ②此两边互为邻边且相交于一点, 则称此多边形为简单多边形[12]。
定义2 多边形的凹凸点 简单多边形中任选相邻2条边pi-1pi和pipi+1, 若此2条边形成的内角大于180°, 则称顶点pi为凹点, 否则称pi为凸点[13]。
算法搜索路径时若路径点落入凹区, 则为完成飞行任务下一路径点须飞离凹区。一方面, 凹区会影响无人机路径的质量如航程变长; 另一方面, 凹区会增加无效路径点数量进而影响解算速度。凸化填充处理步骤如下。
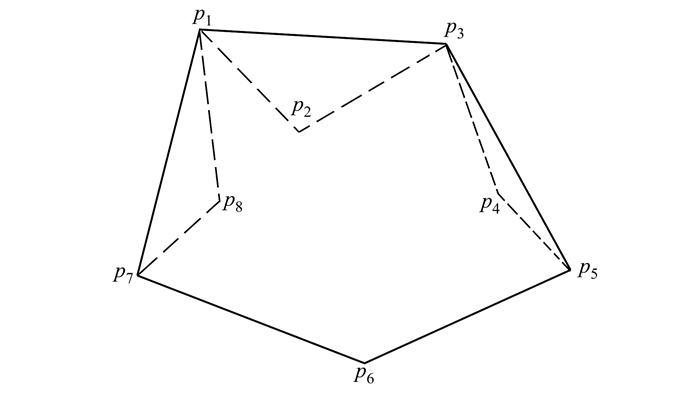
Step1 确定凹多边形F的顶点坐标p1, p2, …, p8, 并判断各顶点的凹凸性;
Step2 从某凸点开始(如p1), 依次连接其余凸点, 凸多边形p1p3p5p6p7p1即为凹多边F的凸化填充处理结果, F≈p1p3p5p6p7p1。
图 3是凹多边形凸化填充处理的结果。
|
| 图 3 凹多边形障碍物凸化填充处理示意图 |
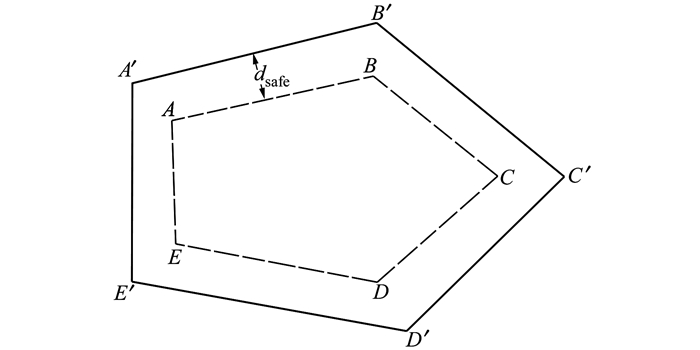
上述处理后不规则障碍物均为凸多边形, 对其进行安全裕度处理较容易。如图 4所示, ABCDE是原多边形障碍物的包线。保持包线形状不变同时将各边向外平移安全裕度dsafe, 各边延长线围成的多边形A′B′C′D′E′即安全裕度处理后的结果。dsafe的大小可由栅格粒度、无人机的安全间隔等决定。
|
| 图 4 多边形障碍物安全裕度建立示意图 |
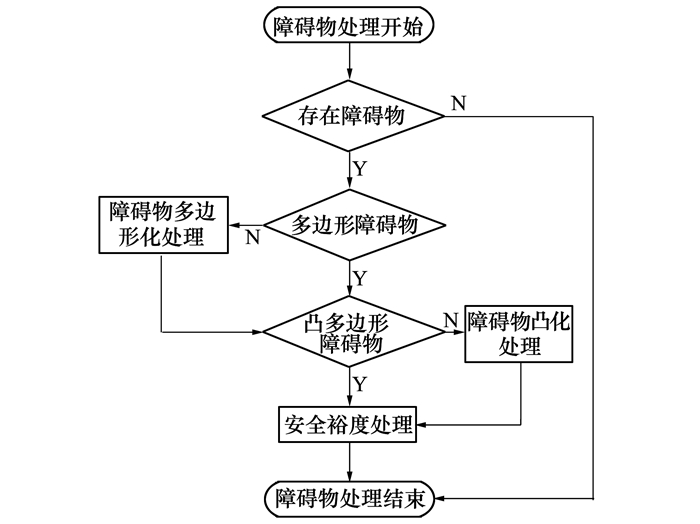
为使无人机飞行路径能避开实际复杂障碍物环境且提高算法求解效率, 需对不规则障碍物进行一系列预处理。综合预处理流程见图 5。
|
| 图 5 不规则障碍物预处理流程图 |
为确保飞行安全, 待选飞行路径点不能落入多边形障碍物区域内。由于本文障碍物经过安全裕度处理, 故可将路径点在障碍物边上归为点在真实障碍物的外部并将无人机在障碍物边上飞行看做是安全的。本文采用射线法判断栅格顶点即待选路径点是否在多边形内部继而决定顶点是否可以作为可飞路径点。
射线法的原理是以点P为端点, 向右方作射线L。因为障碍物是有界的, 所以L的右端在多边形外部。沿着射线从右侧往左看, 当射线和多边形第一次相交时进入多边形内部, 在第二次相交时进入多边形外部, 如此循环就可判断点P与多边形的关系。当射线L和多边形的交点数目n是奇数时, 点P位于多边形内部, n是偶数时点P位于多边形外部[14]。
规划路径时该步检测可实现飞行路径点规避障碍物, 筛除障碍物内部待选路径点, 降低待扩展路径点数目, 同时减少算法搜寻路径时间, 提高搜索效率。
2.2 待选飞行路径段与障碍物相交检测平面几何中线段与多边形的关系有2种:线段与多边形相交、线段与多边形不相交。多边形由线段首尾依次连接而成, 判断线段与多边形是否相交可转化为判断线段与多边形各边是否相交。若线段与多边形任意一边相交, 则线段与多边形相交; 否则线段与多边形不相交。上述过程中判断两线段的相交性是关键一步。
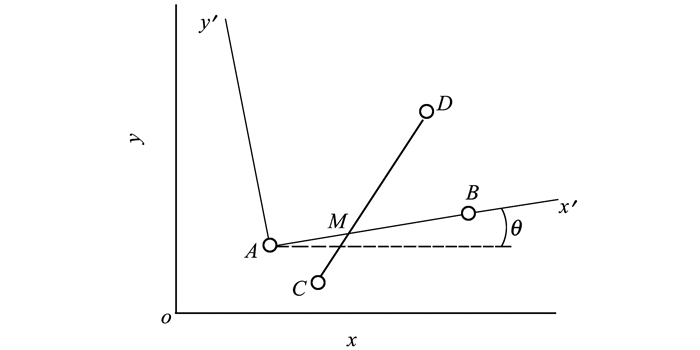
计算机图形学中检测两线段相交的方法有很多, 如向量叉乘法。本文采用一种简便方法来判断两线段的相交性, 原理见图 6。选取障碍物任意一条边记作AB, 无人机待选飞行路径段记作CD。以端点A为原点, 边AB的方向为o′x′轴正方向建立直角坐标系x′o′y′, 则坐标系x′o′y′与原坐标系xoy中点的坐标转换关系式如(4)和(5)式所示
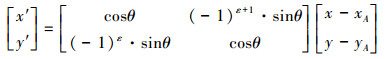
|
(4) |
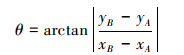
|
(5) |
|
| 图 6 线段相交检测原理图 |
式中:θ为原坐标系ox轴与新坐标系o′x′轴正方向的夹角; ε为判定系数, 当ox轴顺时针旋转θ角得到o′x′轴时, ε取0, 否则ε取1。
依据(4)~(5)式可确定A, B, C, D在x′o′y′中的坐标。记直线AB与直线CD在o′x′轴上的交点为M, 若同时满足以下条件:①y′C>0 & y′D < 0(或y′C < 0 & y′D>0);②x′M≥0;③x′M≤dAB, 则线段AB与CD相交。其中, y′C, y′D分别为C, D点在x′o′y′中的纵坐标, x′M为M点在x′o′y′中的横坐标, dAB为AB的长度。
通过判断无人机待选飞行路径段与多边形障碍物各边是否相交可以判断各待选路径段是否规避障碍物, 进而排除与障碍物相交的路径段同时筛选出与障碍物不相交的无人机可飞路径段。
2.3 障碍物与可飞路径段距离检测无人机一旦进入障碍物区域或离障碍物过近即可认为无人机安全系数低。远离障碍物的路径段能增加无人机的安全系数提高其生存率, 进而提升完成任务的成功率。故规划无人机路径时考虑飞行路径段距障碍物的距离是必要的。
本文定义多边形障碍物到路径段的距离dobs-route为障碍物各顶点pi到路径段l的所有距离中最小的距离, 即

|
(6) |
设计障碍物到无人机飞行路径段的距离最小为目标函数, 对通过相交检测的可飞路径段和障碍物进行距离检测, 最终解算出满足要求的飞行路径。
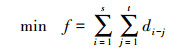
|
(7) |
式中:s为障碍物总个数;t为飞行路径段数目。
求障碍物到路径段的距离可转为求各顶点到路径段的距离, 而计算点到线段的距离主要是判断点到线段两端点的距离与线段长度的大小关系。若已知线段的两端点为A(xA, yA), B(xB, yB)及点P(xP, yP), 则可计算距离dPA, dPB和dAB。点P到线段AB的距离dP-AB可分成3种情况讨论[15]。
Case1 若dPA, dPB和dAB满足(8)式
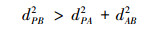
|
(8) |
则点P到线段AB的距离dP-AB为(9)式
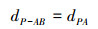
|
(9) |
Case2 若dPA, dPB和dAB满足(10)式
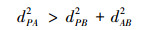
|
(10) |
则点P到线段AB的距离dP-AB为(11)式
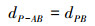
|
(11) |
Case3 若不满足Case1和Case2, 则点P到线段AB的距离dP-AB为(12)式
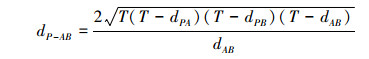
|
(12) |
式中, T满足(13)式
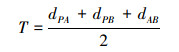
|
(13) |
图 7对以上3种情况形象地说明:若P在区域1, 则P到线段的距离为dPA; 若P在区域2, 则P到线段的距离为dPQ; 若P在区域3, 则P到线段的距离为dPB。

|
| 图 7 点到线段距离的判断图 |
特殊情况下规定障碍物到路径段距离dobs-route为:①路径点位于障碍物内, dobs-route为无穷大; ②路径段与多边形某一边相交, dobs-route为无穷大; ③路径段与多边形某一边重合, dobs-route为0。
2.4 基于IOCAD的无人机路径规划算法设计Step1 判断规划空域中是否存在不规则障碍物, 若存在则进行不规则障碍物综合预处理;
Step2 对于障碍物处理后的规划环境, 采用射线法选出无人机可飞路径点;
Step3 对可飞路径点执行以下操作:
1) 计算可飞路径点中第r个路径点与终点end的连线的斜率K;
2) 计算路径点r与相邻可飞路径点wb的连线斜率krwb并求出满足条件(14)的w最佳, 其中b为相邻可飞路径点的个数
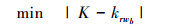
|
(14) |
3) 对w最佳采用相交检测法对路径段rw最佳与所有障碍物进行相交检测, 若通过则将rw最佳作为可飞路径段, 并跳至步骤5), 否则删除wb中与r相邻的可飞路径点w最佳, 并返回步骤2);
4) 若对所有rwb的相交检测都完成且都和障碍物相交, 则路径规划失败, 相交检测结束;
5) 令r=w最佳, 判断路径点w最佳是否为end, 若不是则返回步骤1), 若是则待选飞行路径段与障碍物相交检测结束;
Step4 对可飞路径段求各障碍物到可飞路径段的距离, 并以(7)式为目标函数解算出无人机最终的飞行路径。
3 基于IOCAD的无人机路径规划算法仿真实验及结果分析 3.1 仿真实验环境无人机路径规划的区域为90 km×90 km的矩形区域。假设无人机的最大转弯角为π/4, 最小飞行步长为1 km。不规则障碍物信息见表 1, 在MATLAB中无人机路径规划的初始空域环境见图 8。
| 编号 | 坐标 | 类别 |
| 1 | (40, 10;50, 13;70, 20;60, 36;43, 41;30, 25) | 五边形 障碍物 |
| 2 | (65, 35;85, 35;85, 45;65, 45) | 矩形 障碍物 |
| 3 | (32, 49;60, 58;65, 75;58, 82) | 四边形 障碍物 |
| 4 | (15, 45;20, 50;25, 40;22.5, 75;14, 63) | 凹形 障碍物 |
| 5 | (68, 58;85, 48;75, 82) | 三角形 障碍物 |
| 6 | 中心点位于(22, 25), 长轴为5, 短轴 为8, 倾斜角为π/8的椭圆 | 弧形 障碍物 |

|
| 图 8 路径规划初始空域环境示意图 |
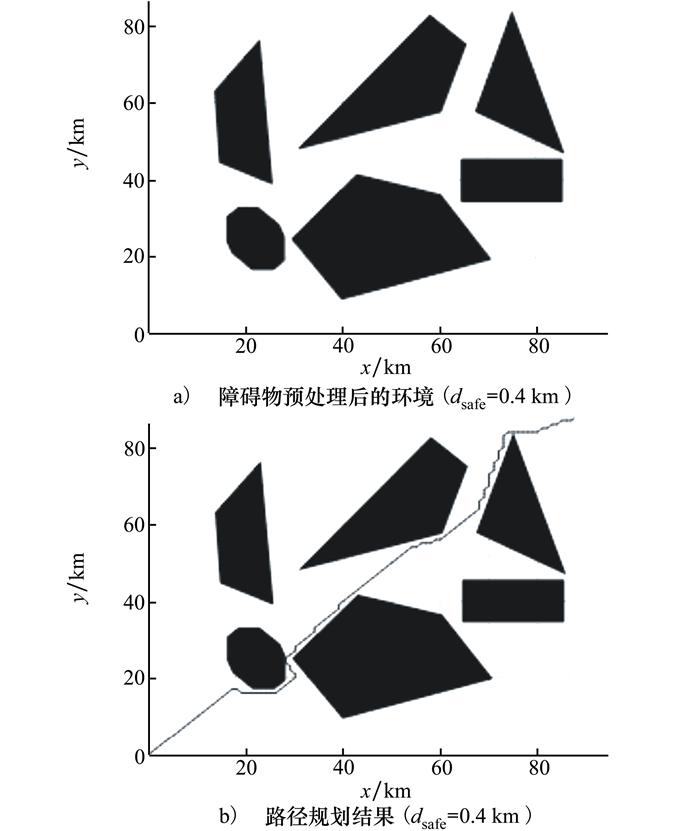
仿真时设置栅格粒度大小Ngrid=1 km, 安全裕度分别为最小飞行步长的0, 0.2, 0.4, 0.6, 0.8和1倍, 即dsafe=0, 0.2, 0.4, 0.6, 0.8, 1 km, 无人机起点坐标(2, 2), 终点坐标(88, 88)。不规则障碍物经弧形障碍物多边形化处理、凹形障碍物凸化处理、安全裕度处理可得障碍物处理后的无人机路径规划环境。图 9是安全裕度为0.4 km时的空域环境及规划出的无人机飞行路径。
|
| 图 9 预处理后环境及飞行路径示意图 |
实际场景中障碍物数目是变化的, 会有新障碍物进入规划空域中。假设新障碍物为静态障碍物且其参数已知。现对环境中新加一个不规则障碍物的情况研究, 新增障碍物信息如表 2所示。
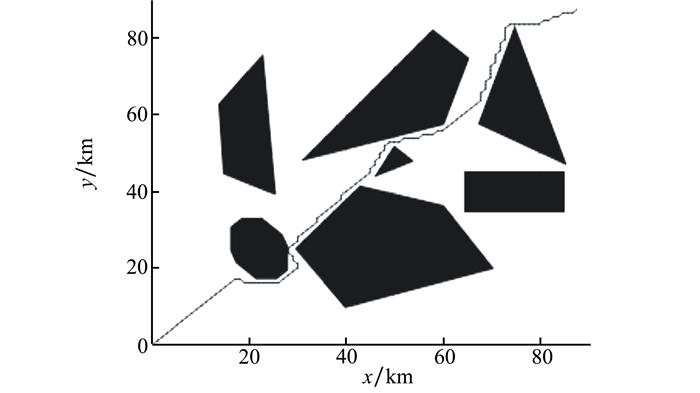
无人机在新增障碍物环境下的路径规划结果如图 10所示。
|
| 图 10 新增障碍物后路径规划结果示意图 |
对于环境中新增的障碍物, 基于IOCAD的无人机路径规划算法可对其有效处理, 使得重规划出的路径成功规避复杂环境中的不规则障碍物。
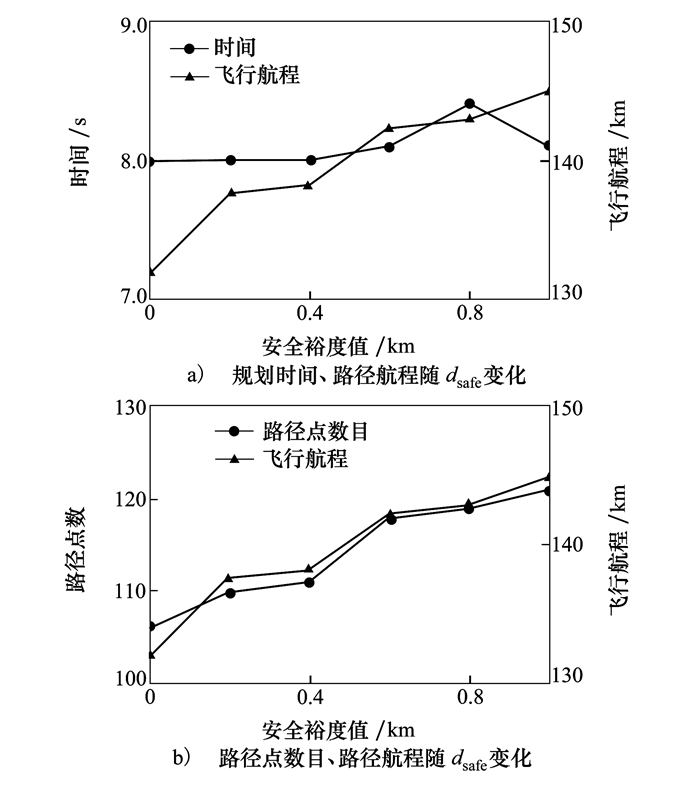
3.3 仿真结果分析图 11给出在不同安全裕度值下无人机路径规划结果的对比。观察可知, 规划时间t、飞行航程L、路径点数目m同安全裕度值呈现相同的变化趋势。随dsafe的增加, 飞行航程急剧增大, 路径点数目也变多, 规划时间增加较缓和。同时发现, 对于规划时间、飞行航程和路径点数目, 以dsafe=0.4为分界线, 在分界线左侧, t, m, L随dsafe变大而平稳上升; 在分界线右侧, t, m, L随dsafe增加的上升率明显增大。故在本仿真中, 当dsafe=0.4 km时可保证算法运行效率最好。实际处理中在考虑无人机距障碍物的安全间隔时, 可通过合理设置安全裕度值达到飞行安全和规划效率的最优平衡。
|
| 图 11 不同安全裕度值下路径规划结果对比示意图 |
图 11中安全裕度为0.4 km的规划用时同无安全裕度的规划用时一样, 规划的路径长度多6.2 km, 占总路径长度的4.5%。考虑到带有安全裕度的障碍物更符合现实情况且能保证无人机的安全, 所以由路径长度变长所带来的代价可忽略不计。
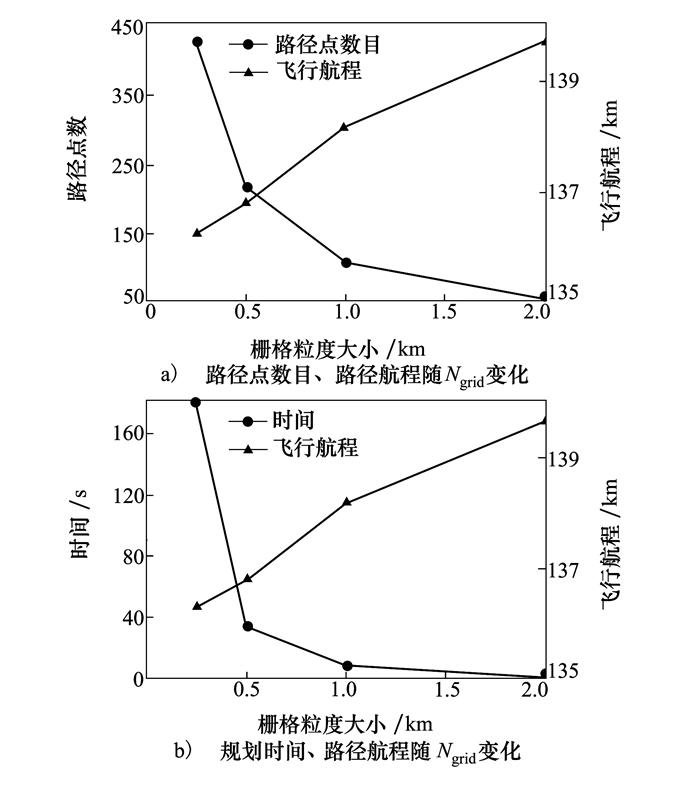
现实环境的复杂性导致不规则障碍物增多, 进行路径段与多边形障碍物相交检测的次数相应增加导致规划用时变长。另外, 栅格法环境建模中选取的栅格粒度小, 栅格划设精细, 导致可搜索节点数目多和规划时间开销大。为缩短规划时间, 本文研究不同栅格粒度大小对于无人机路径规划性能的影响, 找出合理的栅格粒度设置进而提高搜索效率。图 12是在栅格粒度大小Ngrid分别为0.25, 0.5, 1和2 km时, 路径规划结果的对比。
|
| 图 12 不同栅格粒度大小下路径规划结果对比示意图 |
结合图 12可分析, 规划时间t、路径点数目m同栅格粒度的大小呈现相反的变化趋势, 飞行航程L同栅格粒度大小呈现相同的变化趋势。随Ngrid变大, t, m显著减少, 航程L平稳上升。当栅格粒度大小变化时, Ngrid越小, 划设空域精细但搜索点数目增多, 需更多存储空间且耗时长; Ngrid越大, 环境划设粗糙, 路径点减少且效率提高, 但难以保证航程短。同时分析出, 在Ngrid=0.5这条分界线两侧t-Ngrid, m-Ngrid, L-Ngrid曲线的斜率变化率最大。综合上述分析, 本文认为在此仿真环境下, Ngrid=0.5 km为最优的栅格粒度大小设置, 在此设置下能减少规划用时提升算法效率。
仿真实验数据表明:基于IOCAD的无人机路径规划算法能有效解决无人机在复杂、不规则环境下路径规划问题且效率较高。对比仿真数据可知, 安全裕度为0.4 km时, 规划时间相差不多但路径最优; 栅格粒度大小为0.5 km时, 搜索路径点数目少且路径最短。综上所述, 当dsafe=0.4 km, Ngrid=0.5 km时, 本文算法规划的路径航程显著缩短且路径点数有效减少。
4 结论1) 本文采用了一种不规则障碍物预处理方法, 结合射线法选出可飞路径点, 弥补了传统方法创建搜索地图困难的不足。
2) 本文提出的判断两线段是否相交的方法原理简单、算法实现容易, 且将其用于无人机路径规划之中。
3) 基于IOCAD的无人机路径规划仿真实验表明, 在本文不规则障碍物环境下, 该算法可有效规划出无人机避障路径, 且当栅格粒度大小为0.5 km、安全裕度值为0.4 km时, 路径航程短、路径点数目少, 路径最佳。
| [1] | ÖZALP N, SAHINGOZ O K. Optimal UAV Path Planning in a 3D Threat Environment by Using Parallel Evolutionary Algorithms[C]//International Conference on Unmanned Aircraft Systems, 2013 |
| [2] | BIRCHER A, ALEXIS K, BURRI M, et al. Structural Inspection Path Planning via Iterative Viewpoint Resampling with Application to Aerial Robotics[C]//IEEE International Conference on Robotics & Automation, 2015 |
| [3] | BIRCHER A, KAMEL M, ALEXIS K, et al. Three-Dimensional Coverage Path Planning via Viewpoint Resampling and Tour Optimization for Aerial Robots[J]. Autonomous Robots, 2015, 40(6): 1-20. |
| [4] | ROBERGE V, TARBOUCHI M, LABONTE G. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning[J]. IEEE Trans on Industrial Informatics, 2013, 9(1): 132-141. DOI:10.1109/TII.2012.2198665 |
| [5] |
丁家如, 杜昌平, 赵耀, 等. 基于改进人工势场法的无人机路径规划算法[J]. 计算机应用, 2016, 36(1): 287-290.
DING Jiaru, DU Changping, ZHAO Yao, et al. Path Planning Algorithm for Unmanned Aerial Vehicles Based on Improved Artificial Potential Field[J]. Journal of Computer Applications, 2016, 36(1): 287-290. (in Chinese) |
| [6] | TURKER T, SAHINGOZ O K, YILMAZ G. 2D Path Planning for UAVs in Radar Threatening Environment Using Simulated Annealing Algorithm[C]//International Conference on Unmanned Aircraft Systems, 2015 |
| [7] | YAO Peng, WANG Honglun. Dynamic Adaptive Ant Lion Optimizer Applied to Route Planning for Unmanned Aerial Vehicle[J]. Soft Computing, 2016, 21(18): 1-14. |
| [8] |
吴海彬, 林宜. 基于改进Voronoi图的移动机器人在线路径规划[J]. 中国工程机械学报, 2007(1): 117-121.
WU Haibin, LIN Yi. Online Path Planning of Mobile Robots Based on Improved Voronoi Diagram[J]. Chinese Journal of Construction Machinery, 2007(1): 117-121. (in Chinese) DOI:10.3969/j.issn.1672-5581.2007.01.025 |
| [9] |
谢春生, 李雄. 危险天气影响航路飞行区域的划设及评估[J]. 中国安全科学学报, 2010, 20(10): 47.
XIE Chunsheng, LI Xiong. Division and Evaluation of Flight Forbidden Area in Severe Weath[J]. China Safety Science Journal, 2010, 20(10): 47. (in Chinese) DOI:10.3969/j.issn.1003-3033.2010.10.009 |
| [10] | XU Zhuofan, WEI Ruixuan, ZHOU Kai, et al. Laguerre Graph Self-Optimize Path Planning Algorithm for UAVs in Irregular Obstacle Environment[C]//Guidance, Navigation & Control Conference, 2017 |
| [11] |
贾春雪, 罗琦, 龚杨杨. 不规则障碍物的避障路径规划[J]. 计算机科学, 2017, 44(9): 290-295.
JIA Chunxue, LUO Qi, GONG Yangyang. Obstacle Avoidance Path Planning for Irregular Obstacles[J]. Computer Science, 2017, 44(9): 290-295. (in Chinese) |
| [12] |
徐嘉. 二面体群作用下简单多边形的分类[J]. 计算机辅助设计与图形学学报, 2012, 24(7): 896-900.
XU Jia. A Classification Method of Simple Polygons Based on Dihedral Group[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(7): 896-900. (in Chinese) DOI:10.3969/j.issn.1003-9775.2012.07.008 |
| [13] | NICULESCU C P, ROVENTA I. Relative Convexity and Its Applications[J]. Aequationes Mathematicae, 2015, 89(5): 1389-1400. DOI:10.1007/s00010-014-0319-x |
| [14] |
翟艳, 徐卫亚, 张强. 点与多边形或多面体的拓扑关系判断[J]. 计算机工程与设计, 2015, 36(4): 972-976.
ZHAI Yan, XU Weiya, ZHANG Qiang. Judgment of Topological Relation between Point and Polygon or Polyhedron[J]. Computer Engineering and Design, 2015, 36(4): 972-976. (in Chinese) |
| [15] | MA Y, GANG Z, PERRUQUETTI W, et al. Local Path Planning for Mobile Robots Based on Intermediate Objectives[J]. Robotica, 2015, 33(4): 1017-1031. DOI:10.1017/S0263574714000186 |




