2. 红河学院 工学院, 云南 蒙自 661100
工业机器人末端执行器在工作空间的运动轨迹规划是一项重要的内容, 为了确保工业机器人工作质量和延长使用寿命, 需进行平滑无冲击的运动轨迹规划。工业机器人运动轨迹分为位移规划和姿态规划, 姿态规划往往比位移规划复杂得多[1], 本文的研究围绕着工业机器人的姿态规划而进行。
刚体运动姿态的表示方法主要有旋转矩阵、欧拉角和四元数。采用四元数描述姿态主要有如下优点:1)避免出现转动时万向节锁死现象; 2)运算效率更高; 3)便于提供平滑插值。因为其显著的特点, 四元数目前已广泛应用于旋转的场合。四元数描述姿态也有其不利因素, 四元数属于SO(3)旋转空间, 是四维向量, 因此笛卡尔空间的三维向量的运算不适合四元数, 三维向量空间诸多的插值理论不能直接用于四元数姿态插值。在旋转群空间下, 单独利用现有的姿态插补方法并不能够较好地实现多姿态平滑插补, 给四元数姿态插值带来一定困难[2], 因此, 许多相关学者围绕着简洁有效的四元数姿态平滑插值进行大量研究工作。
广泛应用的四元数姿态插值是Shoemake首次提出的球面线性插值SLERP, 其推理过程简洁, 应用简便快捷, 成熟应用于2个姿态之间的插值。但SLERP对2个以上姿态进行插值时, 只能保证C0连续, 在分段点处会出现尖点, 导致插值不平滑, 因此, 球面线性插值SLERP不适合多姿态平滑插值。
为了进行2个以上的四元数多姿态平滑插值, Shoemake在球面线性插值SLERP的基础上提出球面立体插值SQUAD, 但该方法只能保证插值姿态曲线一阶连续性[3], 仍不能满足机器人多姿态轨迹高阶平滑插值的需求。虽然该方法推导与应用稍显复杂, 但也仍是一个较为成熟的算法。
为了进一步提高多姿态轨迹曲线的平滑性, 有学者将四元数样条曲线引入姿态插值中。Kim等首次提出可以高阶可导的四元数样条曲线[4], 它由笛卡尔空间下的样条曲线衍生而来, 并保留了样条曲线的大部分几何特性。该方法提出样条曲线的累和基函数概念, 姿态插补以样条曲线的累和基函数作为四元数的指数进行运算, 一方面累和基函数较复杂, 另一方面四元数是属于旋转空间, 四元数的指数运算较繁锁, 给插值运算带来一定的难度。再有, 用贝赛尔、B-spline四元数样条曲线姿态插值时, 构造过程中需要反算单位四元数曲线的控制顶点, 但由于单位四元数曲线是在非欧氏空间生成, 所求其控制顶点需要解非线性方程组, 因此只能够近似求解得出曲线控制点的数值解[5]。
Ge等[6]提出了构造二阶连续的单位四元数B-spline曲线算法, 虽然构造过程中相关约束方程是非线性的, 然而给出了2个额外四元数计算法则可获得精确单位四元数控制顶点。不足之处是该方法计算比较复杂, 而且单位四元数型值点局限于某种给定的约束条件。Miura等[7]提出了四元数样条曲线的积分曲线, 该曲线具有简单的曲率表达形式。这两种方法都需要复杂的数值积分和大量的迭代运算[8], 不利于工业机器人高效运作。
邢燕等[9]提出一种快速生成单位四元数插值样条曲线, 通过选择适当的四次多项式调配函数, 然后通过累和基函数作指数, 代表关键帧方向的单位四元数为底的指数函数的连乘形式把欧氏空间中的样条曲线推广到单位四元数空间S3中, 该方法不需要反求控制点, 但插值曲线的光顺不如B样条曲线。
虽然存在大量单位四元数曲线构造方法, 仍然很难判断某个方法比其他方法更好, 至今也没有完美的解决方案[10], 相关研究人员一直努力朝着这个方向研究探索。本文旨在寻求一种简洁有效的四元数多姿态平滑插值的方法。
1 四元数与姿态 1.1 四元数运算与性质四元数一般表示方法为q=w+xi+yj+zk, 也可写成q=[w, (x, y, z)]=[w, v], w称为四元数的实部, v称为四元数的虚部或复数部。四元数q实部为零, 即w=0, q=[0, (x, y, z)]时, 称q为纯四元数。当四元数q的模等于1时, 即‖q‖=
任意2个四元数:p=[p0, u], q=[q0, v], 其乘法可表示为
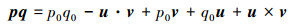
|
(1) |
从(1)式中可以看出, 四元数的乘法较复杂, 四元数是四维向量, 其运算不能直接运用三维向量的运算方法。当这2个四元数是纯四元数, 即p0=q0=0, 公式(1)可简化为
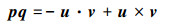
|
(2) |
单位四元数还可用转角与转轴矢量表示

|
(3) |
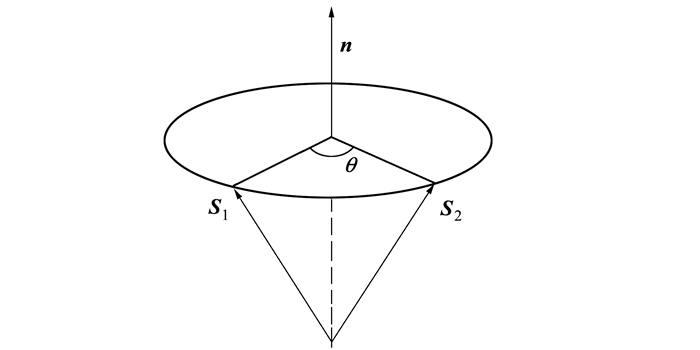
式中, θ为转角, n=(a, b, c)为转轴矢量, 也即转轴在笛卡尔空间的坐标位置。刚体上任一点s1=(x1, y1, z1), 如图 1所示, 可对应写为纯四元数S1=[0, (x1, y1, z1)], 绕转轴n转动θ角之后变化到新的位置点s2=(x2, y2, z2), 该点可对应写为纯四元数S2=[0, (x2, y2, z2)], 该质点转动前后的坐标关系用四元数数学方程描述为:S2=qS1q-1。四元数物理意义明显, 一个四元数对应一个转动。
|
| 图 1 质点矢量旋转 |
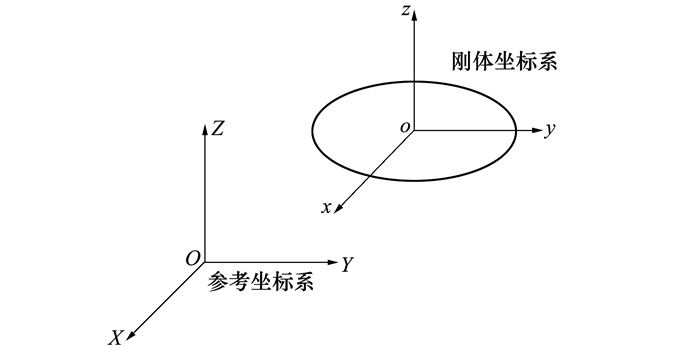
当刚体发生转动时, 不仅是刚体上质点的位置矢量发生变化, 并且整个刚体的方位朝向也发生了变化。假设刚体质心固连着一个坐标系oxyz, 该固连坐标系在没有转动之前与参考坐标系(即绝对坐标系)OXYZ方位朝向是相同的, 如图 2所示。
|
| 图 2 刚体固连坐标系初始位置 |
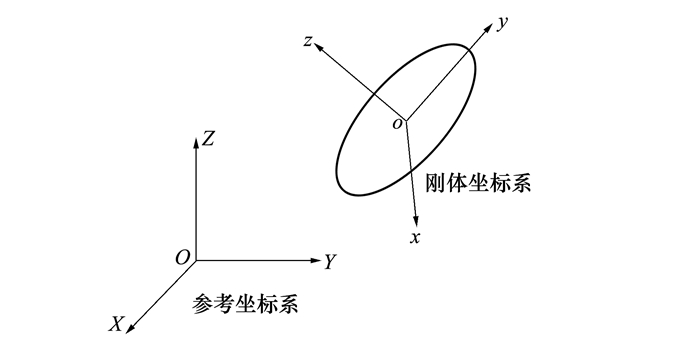
当刚体发生转动时, 坐标系方位朝向就不再与参考坐标系重合了, 也即姿态发生了改变。参考坐标系OXYZ称为静坐标系, 刚体上固连坐标系oxyz称为动坐标系, 动坐标系与静坐标系之间的方位关系称为姿态, 如图 3所示。
|
| 图 3 刚体固连坐标系转动之后的姿态 |
姿态一般可采用下面3种方法表示:
1) 刚体姿态采用变换矩阵表示
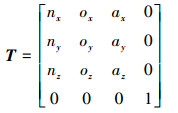
|
(4) |
式中, (nx, ny, nz)是动坐标系的x坐标轴相对于参考坐标系OXYZ的3个方向余弦, 同理, (ox, oy, oz)是y坐标轴相对于参考坐标系的3个方向余弦, (ax, ay, az)是z坐标轴相对参考坐标系的3个方向余弦。变换矩阵表示刚体姿态时, 需要9个元素, 运算效率低, 而且不便于进行姿态平滑插值。
2) 欧拉角表示刚体姿态。刚体绕着动坐标系下坐标轴的转动广泛地称为欧拉角, 欧拉角转动顺序不可逆, 例如, 刚体欧拉角绕动坐标系轴的转动顺序为αx→βy→γz, 如果转动的次序发生改变, 虽然欧拉角没有变, 但得到的最终姿态是不相同的。无论怎么样的转动次序, 当第二个转动角为±90°时[11], 会出现的“Gimbal Lock”现象, 刚体失去一个自由度, 将不按预期的路径运动, 称为万向节锁死现象, 因此欧拉角进行姿态插值时, 如何避免万向节锁死是个难点。
3) 四元数表示刚体姿态。如前面所述, 一个四元数就意味着一个转角及转轴矢量, 一个四元数其物理意义就是代表着一个转动, 所以四元数显然可以用来描述刚体姿态。四元数, 只需要4个元素, 运算速度快, 并且不会出现万向节锁死现象。采用四元数进行姿态插值优势明显, 但四元数也有其弱点, 因为四元数是四维向量, 不能直观地在笛卡尔空间中表现出来, 并且三维向量的运算法则与插值法则不能直接运用在四元数上, 因而给四元数姿态插值带来一定的难度。
2 基于对数四元数的样条曲线姿态插值原理 2.1 对数四元数插值原理如前所述, 四元数是四维向量, 三维向量的插值方法以及平滑的三维样条曲线不能直接用于四元数插值, 需要进行处理。
如公式(3)所示, 任一个四元数q, 可表示为:q=[cos(θ/2), sin(θ/2)·n], 其中, θ为转角, n=(a, b, c)为转轴矢量。式中四元数代入运算的角度值是转角θ的一半, 即带入式中计算的角度值为θ/2。不难证明对于单位四元数q, 其对应的转轴矢量n为单位矢量, 即转轴矢量的模为1, ‖n‖=1。
对于一个单位平面复数F=A+Bi, 其模‖F‖=1, 幅角ϕ=arctan(B/A), 可把该单位复数写成指数形式F=eϕi。四元数是比平面复数更复杂的复数, 同样的道理, 也可以把单位四元数q相应写成指数形式

|
(5) |
当对(5)式两边取对数, 得到
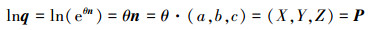
|
(6) |
从(6)式中可以看出, 四维四元数q取对数之后转换为笛卡尔空间的三维坐标点P, 可进行相应的插值。给定起始姿态qs与结束姿态qe, 根据(6)式可得到三维空间起始点Ps与结束点Pe, 这时就可以运用三维空间的各种插值方法进行插值, 得到一系列插值点Pi=(Xi, Yi, Zi) i=0, 1, 2, …, n, 根据相关插值方程把插值点写成:P(t)=[X(t), Y(t), Z(t)]t∈[0, 1]。三维空间完成插值之后, 需要转换为四维空间的单位四元数, 要保证旋转轴矢量为单位转轴, 即要对旋转轴矢量进行单位化, 则改为

|
(7) |
将(7)式中P(t)的表达式代入到(6)式中, 然后等式两边再取指数, 得到
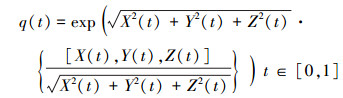
|
(8) |
将(8)式与(5)式进行类比, 得到插值单位四元数的旋转角与旋转轴矢量
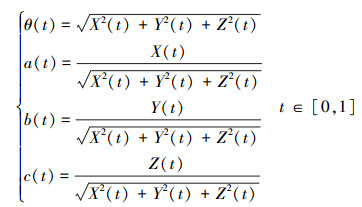
|
(9) |
最后可以推导出插值单位四元数的实部与复数部
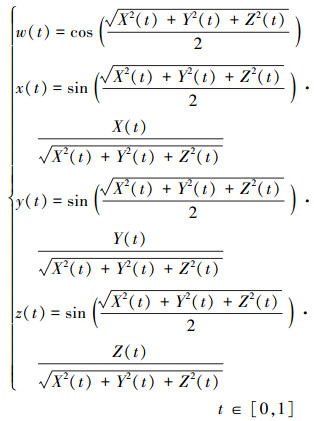
|
(10) |
通过上述方法, S3空间的四元数可转换为R3笛卡尔空间的三维向量, 然后进行相应的三维样条曲线插值, 各插值点经过单位化之后又可转化到旋转空间, 从而可以映射到四元数空间, 完成四元数姿态样条曲线插值。
由(5)至(6)式可得到(11)式
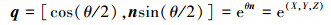
|
(11) |
从(11)式中可以看出, 样条曲线经过取指数之后, 必然保持其连续性特性, 取指数就是样条曲线映射到四元数空间的过程, 因而对应的四元数也保持相应的连续性特性, 连续性的阶次不变。
2.2 Hermite样条曲线插值在曲线变化不是很剧烈的情况下, 三次多项式样条函数是一种很好的拟合插值工具, 构造的曲线可达到二阶连续[12], 能够解决许多生产实际问题, 因此在工程中有一定的应用。文献[12]介绍了Hermite三次多项式插值二维平面曲线的原理推导及相关方程, 没有直接给出插值三维空间曲线的相关方程, 经过进一步的细化, 可以得到三维空间中样条曲线的Hermite插值方程。
实践证明, 取累加弦长作为参数变量比较理想, 且能很好的拟合弯曲变化比较剧烈的插值曲线。累加弦长表达如(12)式所示

|
(12) |
式中, Pj(xj, yj, zj) j=0, 1, 2, …, n是给定的型值点, 按次序排放的型值点之间距离之和也就是样条曲线的累加弦长sk。按次序排放的每两个型值点就决定一条空间样条曲线, 因此可以得到多段样条曲线。
在二维平面中分段Hermite三次样条曲线的基础上, 可得到分段的三维空间Hermite三次样条曲线方程。需要说明的是, 此时样条曲线取值区间发生了变化, 由x坐标轴上的区间变成了弦长区间。
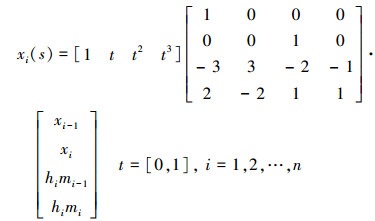
|
(13) |
式中, xi(s)是指第i段弦长区间第i段样条插值曲线x坐标值, xi-1, xi是第i段样条曲线给定型值点的x坐标值, hi是第i段样条曲线弦长区间长度, 可由(14)式求得。mi-1, mi是第i段样条曲线在型值点处的一阶导数。通常情况下, 对于整个样条曲线, 已知首末两端型值点的一阶导数m0, mn, 但中间型值点的一阶导数m1, m2, …, mn-1是未知的, 需要通过(15)式追赶法求解。
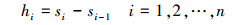
|
(14) |
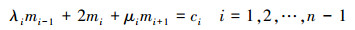
|
(15) |
在(15)式中, 通常情况下, 对于整个区间, 要给出第一个端点和最后一端点的一阶导数, 也就是m0, mn是已知, 需要求取m1, m2, …, mn-1, 就必须给出(15)式中其他相关系数的求法, 如(16)式所示。
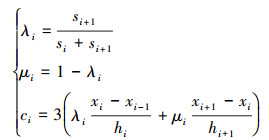
|
(16) |
需要指出的是(16)式中, si是指第1段样条曲线至第i段样条曲线的累加弦长, 并不是指第i段样条曲线的弦长。
将(16)式中的系数代入(15)式中, 就可以求得中间型值点的一阶导数, 再代入(13)式中, 可以求得各段插值样条曲线的xi(s)坐标值。
用同样的方法, 只要分别将型值点的y, z坐标值、一阶导数以及相关系数代入上述方程, 就可以求得各段插值样条曲线的yi(s), zi(s)坐标值, 最后得到完整的多段Hermite三维空间样条插值曲线。
2.3 基于对数四元数的Hermite样条曲线姿态插值步骤综上所述, 可将工业机器人对数四元数法的Hermite样条曲线多姿态插值步骤描述如下:
步骤1 根据工业机器人作业任务, 得到末端执行器有限个关键姿态, 将这些有限的关键姿态转换为四元数形式q1, q2, …, qn。
步骤2 根据(6)式, 对四元数取对数, 即可得到笛卡尔空间相应的型值点P1, P2, …, Pn, 四元数四维向量转化为三维向量。
步骤3 运用Hermite三次多项式样条曲线对型值点P1, P2, …, Pn进行插值, 得到n-1段插值样条曲线。
步骤4 通过(9)至(10)式将n-1段插值样条曲线的插值点单位化之后映射到四元数空间, 从而得到单位四元数的姿态插值。
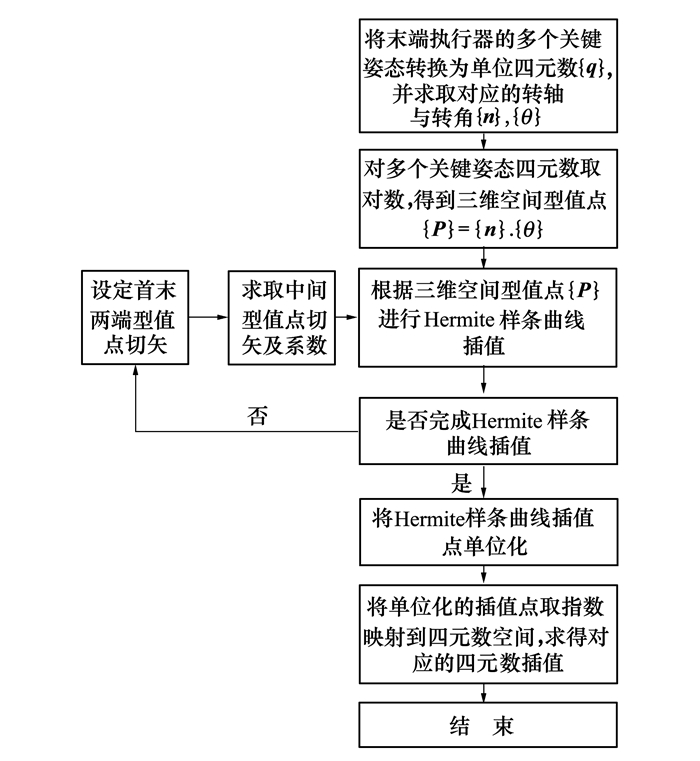
该插值步骤的程序流程图如图 4所示。
|
| 图 4 插值步骤的程序流程图 |
为了检验本文提出方法的正确性与合理性, 运用相关算例进行验证。
算例 工业机器人为了完成某项工作任务, 末端执行器要经历3个必要的姿态, 第一个姿态为绕参考坐标系X转30°, 第二个姿态为绕参考坐标系Y转45°, 第三个姿态为绕参考坐标系Z转60°, 运用本文介绍的Hermite样条曲线进行四元数多姿态插值, 均匀插补中间姿态。
该算例的姿态插值过程如下:
1) 末端执行器第一个姿态用四元数表示, q1=[0.965 9, 0.258 8, 0, 0];第二个姿态用四元数表示为, q2=[0.923 9, 0, 0.382 7, 0];第三个姿态用四元数表示为, q3=[0.866, 0, 0, 0.5]。
2) 第一个四元数姿态q1转化为转角θ1与转轴矢量n1的形式, 得到θ1=0.523 6, n1=[1, 0, 0], 按(6)式得到笛卡尔坐标系中Hermite样条曲线的第一个型值点P1=θ1·n1=[0.523 6, 0, 0]。用同样的方法, 可以得到第二、三个姿态对应的第二、三个型值点, P2=[0, 0.785 4, 0], P3=[0, 0, 1.047 2]
3) 用求得的3个型值点P1, P2, P3, 进行Hermite三次样条曲线插值。需要给定首、末两端型值点的一阶导数, 在没有指定要求情况下, 不防如此设定, 单位切矢由3个坐标轴方向平均分配, 故首个型值点一阶导数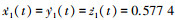

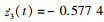
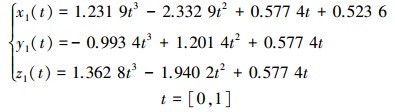
|
(17) |
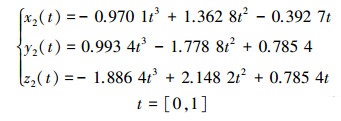
|
(18) |
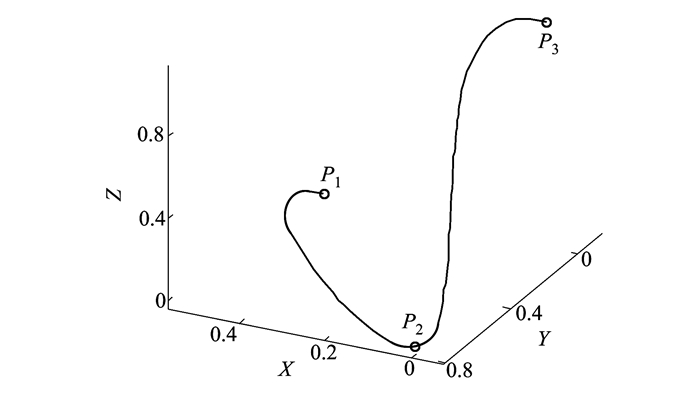
如图 5所示, 型值点P1, P2之间构成第一段Hermite样条曲线, 型值点P2, P3之间构成第二段Hermite样条曲线, 由(17)至(18)式可以验证, 这两段样条曲线是三阶连续的, 连接这两段样条曲线的公共型值点P2处是二阶连续的, 因此整个样条曲线是二阶连续的。
|
| 图 5 Hermite插值样条曲线 |
4) 根据选取不同的参数t, 可在两段样条曲线取一定数量的插值点, 按(9)至(10)式可将这些三维空间的插值点映射到四元数空间, 就可以得到相应的插值四元数。按(8)式将Hermite三次样条曲线经过单位化之后, 就可转换到旋转空间, 从而可以映射到四元数空间。如(11)式所示, 最终的四元数插值过程可看成是Hermite三次样条曲线取对数, 必然保持其二阶连续性, 因而对应的四元数也保持二阶连续性。
仅取t=0, 0.2, 0.5, 1为例, 求得第一段样条曲线相应的插值点坐标, 再把三维空间的这些插值点映射到四元数空间得到四元数插值, 运算结果列入表 1中。为了便于区分, 笛卡尔空间的坐标值用大写字母表示。
| 序号 | 参数 ti |
样条曲线坐标值 | 转角 θ/rad |
转轴矢量 | 插值四元数 | ||||||||
| 实部 | 虚部 | ||||||||||||
| X | Y | Z | a | b | c | w | x | y | z | ||||
| 1 | 0 | 0.523 6 | 0 | 0 | 0.523 6 | 1 | 0 | 0 | 0.965 9 | 0.258 8 | 0 | 0 | |
| 2 | 0.2 | 0.555 6 | 0.155 6 | 0.048 8 | 0.579 1 | 0.959 5 | 0.268 7 | 0.084 2 | 0.958 4 | 0.273 9 | 0.076 7 | 0.024 1 | |
| 3 | 0.5 | 0.383 1 | 0.464 9 | -0.026 0 | 0.602 9 | 0.635 3 | 0.771 0 | -0.043 1 | 0.954 9 | 0.188 6 | 0.228 9 | -0.012 8 | |
| 4 | 1 | 0 | 0.785 4 | 0 | 0.785 4 | 0 | 1 | 0 | 0.923 9 | 0 | 0.382 7 | 0 | |
从表 1中可以看出, 当t=0时, 第一段样条曲线上的第一个点映射到四元数空间, 求得的四元数与第一个姿态q1一致; 当t=1时, 第一段样条曲线上的最后一个点映射到四元数空间, 求得的四元数与第二个姿态q2一致。
同理, 仅取t=0, 0.2, 0.5, 1为例, 求得4组第二段样条曲线映射四元数的数据, 如表 2所示。
| 序号 | 参数 ti |
样条曲线坐标值 | 转角 θ/rad |
转轴矢量 | 插值四元数 | ||||||||
| 实部 | 虚部 | ||||||||||||
| X | Y | Z | a | b | c | w | x | y | z | ||||
| 1 | 0 | 0 | 0.785 4 | 0 | 0.785 4 | 0 | 1 | 0 | 0.923 9 | 0 | 0.382 7 | 0 | |
| 2 | 0.2 | -0.031 8 | 0.722 2 | 0.227 9 | 0.758 0 | -0.041 9 | 0.952 8 | 0.300 7 | 0.929 0 | -0.015 5 | 0.352 5 | 0.111 3 | |
| 3 | 0.5 | 0.023 1 | 0.464 9 | 0.694 0 | 0.835 6 | 0.027 6 | 0.556 3 | 0.830 5 | 0.913 9 | 0.011 2 | 0.225 7 | 0.336 9 | |
| 4 | 1 | 0 | 0 | 1.047 2 | 1.047 2 | 0 | 0 | 1 | 0.866 0 | 0 | 0 | 0.5 | |
从表 2中可以看出, 当t=0时, 第二段样条曲线上的第一个点映射到四元数空间, 求得的四元数与第二个姿态q2一致; 当t=1时, 第二段样条曲线上的最后一个点映射到四元数空间, 求得的四元数与第三个姿态q3一致。
当t在取值区间均匀取值时, 例如取Δt=0.02时, 可以分别得到50组第一段及第二段样条曲线的插值与映射的数据, 完成四元数姿态插值。
图 6是本算例末端执行器姿态插值时转动角变化曲线, 从图中可以看出, 初始转角为0.524, 与第一个姿态一致, 序列为50时, 转角为0.786与第二个姿态符合。最后的转角为1.047, 与最后姿态一致。并且可以从图中看出转角变化曲线没有出现断点或尖点, 转角变化曲线不仅连续而且平滑。

|
| 图 6 转角变化曲线 |
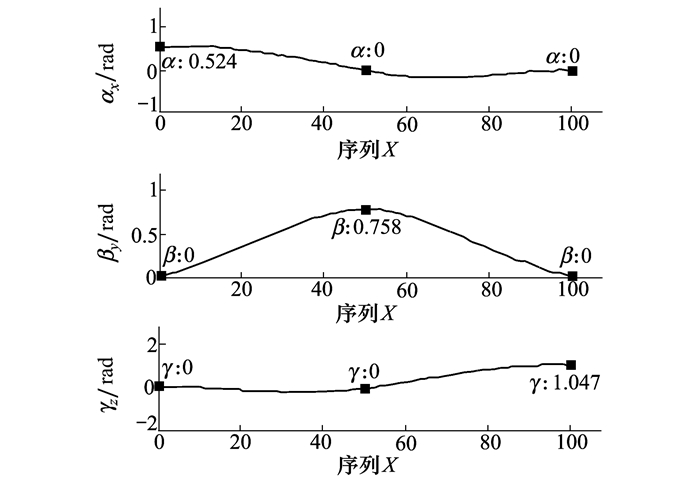
用转动角与转轴矢量来表示的旋转运动可转化为绕3个动坐标轴转动的复合欧拉角。如图 7所示, 初始欧拉角为(αx, βy, γz)=(0.524, 0, 0), 与第一个姿态一致。序列为50时, 欧拉角为(αx, βy, γz)=(0, 0.786, 0), 与第二个姿态一致。最后的欧拉角为(αx, βy, γz)=(0, 0, 1.047), 与最后一个姿态一致。从图 7中可以看出3个欧拉角没有出现间断点或尖点, 说明欧拉角变化曲线是连续且平滑的。
|
| 图 7 欧拉角变化曲线 |
图 8是转轴矢量变化曲线图, 从图中可以看出, 初始转轴矢量为(a1, b1, c1)=(1, 0, 0), 与第一个姿态转轴矢量一致。中间转轴矢量为(a2, b2, c2)=(0, 1, 0), 与第二个姿态转轴矢量一致。最后转轴矢量为(a3, b3, c3)=(0, 0, 1), 与第三个姿态的转轴矢量一致。并且从图中可以看出转轴矢量变化曲线没有出现尖点或间断点, 说明转轴矢量变化也是连续且平滑的。

|
| 图 8 转轴矢量曲线 |
如上所述, 对多个姿态进行四元数插值时, 用本文方法得到的转角及转轴矢量变化都是连续且平滑的。为了进一步比较说明, 上面的算例再运用SLERP插值方法进行多个姿态的插值, 与本文提出的插值方法得到的结果进行对比。
SLERP插值方法成熟地应用于2个四元数姿态之间的插值, 但如果对2个以上的四元数多姿态插值时, SLERP插值方法的平滑性就变得很差。
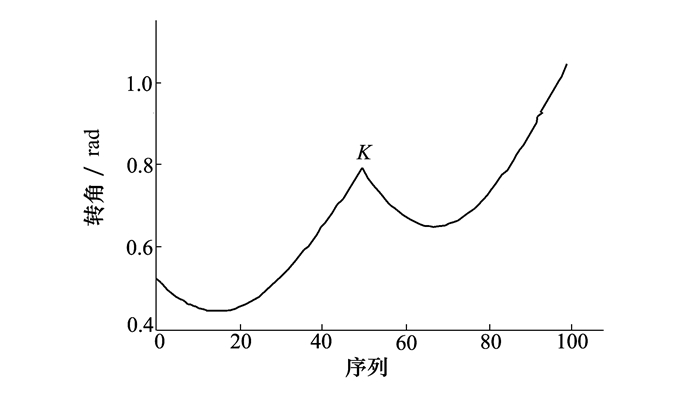
图 9是用SLERP方法进行四元数多姿态插值得到的转角变化曲线图, 从图中可以直观看出, 虽然转角变化曲线是连续的, 但在K点处出现明显的尖点, 曲线不平滑, 在尖点处, 会对机械臂产生冲击, 对工业机器人的作业质量以及使用寿命均产生不良影响。
|
| 图 9 Slerp多姿态插值转角曲线 |
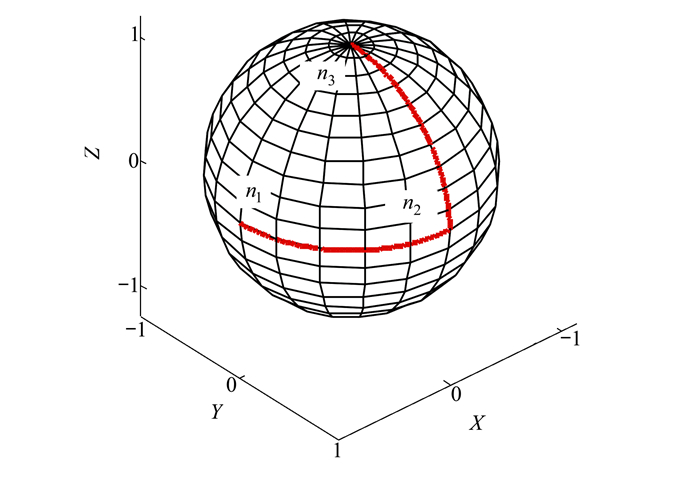
图 10为用SLERP插值方法进行四元数多姿态插值得到的转轴矢量变化曲线图, 从图中也可以看出变化曲线虽然是连续的, 但在n2点处有明显尖点, 转轴矢量曲线不平滑。这种姿态规划必然对机械手末端执行器产生冲击, 影响机械手的作业质量和使用寿命。
|
| 图 10 Slerp多姿态插值转轴矢量曲线 |
相对比而言, 本文提出的基于对数四元数样条曲线姿态插值能保持插值的平滑性。Hermite样条曲线的分段样曲线是三阶连续的, 并且在分段点处具有二阶连续性, 所以整个样条曲线是二阶连续的, 能保证曲线的平滑性。Hermite样条曲线按(11)式取指数之后, 就可映射到旋转空间, 就可转化为对应的四元数。连续函数取指数之后仍保持其连续性, 因而对应的四元数也保持二阶连续性, 所以能保证机械手末端执行器姿态插值的平滑性, 减少冲击与震动, 对工业机器人的工作质量、使用寿命等方面均有益处。
4 结论平滑的姿态插值对工业机器人的工作质量、使用寿命等有着明显的影响作用, 四元数因为其优点广泛用于姿态插值, 但由于四元数属于旋转空间, 是四维向量, 笛卡尔坐标系下平滑的三维样条曲线插值不能直接用于四元数的插值, 因而如何把笛卡尔三维空间的样条曲线插值应用于四元数多姿态插值有着明显的研究意义。
本文提出一种可以把三维样条曲线映射到单位四元数空间的方法。四元数写成转轴矢量与转轴的指数形式, 对其取对数之后四元数就可转换到三维空间, 此时就可运用三维空间的样条曲线插值方法进行插值, 得到相应的插值点之后进行向量单位化, 然后可写为转轴矢量与转角的形式, 之后再取指数, 在三维空间的插值点最后就可映射到四元数空间, 实现四元数姿态平滑插值并保持其连续性。
结合文中四元数多姿态插值的算例, 详细介绍了Hermite样条曲线运用该方法进行多姿态平滑插值的原理与步骤, 得到的插值结果和图形验证了该方法进行多姿态插值的合理性与正确性。该方法具有构造方法简单、易于实现、直观易理解的特点。该方法除了适用于Hermite样条曲线的四元数多姿态插值, 还可延伸到贝赛尔曲线、B样条曲线等样条曲线上。
| [1] | SAEED B N. Introduction to Robotics:Analysis, Control, Application[M]. 2nd Edition. Hoboken, New Jersey: John Wiley & Sons Inc, 2010. |
| [2] | TAN J, XING Y, FAN W, et al. Smooth Orientation Interpolation Using Parametric Quintic-Polynomial-Based Quaternion Spline Curve[J]. Journal of Computational and Applied Mathematics, 2018, 329: 256-267. DOI:10.1016/j.cam.2017.07.007 |
| [3] |
季晨.工业机器人姿态规划及轨迹优化研究[D].哈尔滨: 哈尔滨工业大学, 2013 JI Chen. Research on Orientation Interpolation and Optimal Trajectory of Industrial Robot[D]. Harbin, Harbin Institute of Technology, 2013(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D417439 |
| [4] | KIM M J, KIM M S, SHIN S Y. A General Construction Scheme for Unit Quaternion Curves with Simple High Order Derivatives[J]. Computer Graphics, 1995, 29(3): 369-376. |
| [5] |
许任政.刚体朝向轨迹中四元数样条曲线的研究[D].合肥: 合肥工业大学, 2016 XU Renzheng. Research on the Orientation Spline Curves of the Rigid Body Orientation Trajectory[D]. Hefei, Hefei University of Technology, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10359-1016211430.htm |
| [6] | GE W, HUANG Z, WANG G. Interpolating Solid Orientations with a C2 Continuous B-Spline Quaternion Curve[C]//International Conference on Technologies for E-Learning and Digital Entertainment, 2007: 606-615 |
| [7] | MIURA K. Unit Quaternion Integral Curve:a New Type of Fair Free-Form Curves[J]. Computer Aided Geometric Design, 2000, 17(l): 39-58. |
| [8] |
王效杰.基于四元数样条曲线的姿态轨迹规划研究[D].绵阳: 西南科技大学, 2012 WANG Xiaojie. Research on Orientation Trajectory Planning Based on Quaternion Spline Curve[D]. Mianyang, Southwest University of Science and Technology, 2012(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10619-1015318269.htm |
| [9] |
邢燕, 樊文, 檀结庆, 等. 一类C2连续的单位四元数插值样条曲线[J]. 计算机辅助设计与图形学报, 2016, 29(1): 45-51.
XING Yan, FAN Wen, TAN Jieqing, et al. A C2-Continuous Unit Quaternion Interpolatory Spline Curve[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 29(1): 45-51. (in Chinese) |
| [10] | KIM M S, NAM K W. Hermite Interpolation of Solid Orientations with Circular Blending Quaternion Curves[J]. Computer Animation & Virtual Worlds, 2015, 7(2): 95-110. |
| [11] |
赵晓颖, 温立书, 么彩莲. 欧拉角参数表示下姿态的二阶运动奇异性[J]. 科学技术与工程, 2012, 12(3): 634-637.
ZHAO Xiaoying, WEN Lishu, YAO Cailian. The Second-Order Kinematic Singularity of Orientation in Euler Parameters[J]. Science Technology and Engineering, 2012, 12(3): 634-637. (in Chinese) DOI:10.3969/j.issn.1671-1815.2012.03.036 |
| [12] |
常智勇, 万勇. 计算机辅助几何造型技术[M]. 3版. 北京: 科学出版社, 2013.
CHANG Zhiyong, WAN Yong. Computer Aided Geometric Design Technology[M]. 3rd Edition. Beijing: Science Press, 2013. (in Chinese) |
2. College of Engineering, Honghe University, Mengzi 661100, China


