迭代学习控制(ILC)作为一种前馈控制技术, 主要应用于具有重复运动性质的被控对象, 可在给定的时间范围内实现高精度跟踪给定期望轨迹[1]。在很多轨迹跟踪控制要求较高的重复运动系统中获得了广泛应用, 如机器人[2]、电动机[3-4]、光刻机[5]、珩磨机[6]等。
迭代学习控制最优增益可以保证系统快速收敛, 经过有限次迭代后达到最小系统收敛误差[7-9], 但是目前最优增益的取值研究主要集中在无干扰的线性系统中, 仅考虑理想系统的最优控制增益精确解, 忽略了系统扰动及外部干扰对最优增益的影响[10]。Stefan等[11]考虑了线性离散时间系统的迭代学习控制问题, 利用迭代矩阵范数与范数之间的关系, 得到跟踪误差的2-范数随着迭代次数增加而单调减小并趋于零的结论。Hatzikos等[12]在时变系统中引入遗传算法获取范数最优ILC输入向量, 取得了较好的收敛效果, 但该方法忽略了干扰的影响且难以应用于其他复杂ILC算法。Madady[13]提出了基于范数的LTI系统PID型ILC增益优化设计方法, 可以通过较少的计算量获得接近最优的收敛特性, 但是该研究中主要针对理想LTI系统进行分析, 不包括系统扰动及输出干扰。针对这一问题, Madady[14]针对一类存在系统扰动及输出干扰的LTI进行了分析研究, 但是从推导过程来看, 这一类系统扰动和输出干扰是迭代过程中重复出现的周期性误差, 该误差对于最优控制增益的求解不产生影响。傅勤[15]将Jacobi方法引入到迭代学习控制并构建了线性迭代学习控制与线性方程组之间的联系, 由此构架得到新的迭代学习控制律, 但是该控制律成立的条件过于严格, 实际上减小了满足系统收敛充要条件的区域大小, 一定程度上限制了该算法的应用。兰天一等[16]针对LTI系统设计了一种区间可调节的具有指数加速的闭环ILC算法, 该方法根据每次迭代学习效果确定下次迭代的区间并修正控制增益, 与传统ILC算法相比可以有效提升系统收敛速度, 但是该算法的控制增益初始值仍然是根据经验进行选定, 针对该算法控制增益初始值的最优化处理将进一步提升系统收敛速度。
而在实际运动控制系统中, 系统扰动及外部干扰不可避免, 为有效减小扰动对系统轨迹跟踪性能的影响并增强系统鲁棒性, 研究者提出了带遗忘因子迭代学习控制方法进行跟踪控制[17-19]。该方法可以有效抑制上次迭代过程中控制向量引起的系统输出误差波动, 使本次迭代的输出误差趋近于稳定值, 消除系统扰动引起的误差累积, 但是该方法的缺点也很明显, 遗忘因子的引入将导致系统输出误差不能趋近于零, 只能保证收敛到零点的某一邻域内[20-21]。因此, 研究带遗忘因子ILC算法中存在干扰时的最优控制增益, 将会引出新的问题:引入遗忘因子后收敛条件有无变化?如何保证系统快速单调收敛?如何在遗忘因子ILC算法中求得具体的最优增益值?以上问题都具有实际意义, 但是目前尚无相关的研究论文。
针对上述问题, 本文提出基于最优增益方法的带遗忘因子ILC算法, 利用系统状态方程参数及迭代矩阵特性, 研究遗忘因子对系统收敛特性的影响, 构建系统最优控制增益, 使含非严格重复扰动系统输出跟踪误差波动减小, 在快速收敛的同时保证输出跟踪误差收敛到零的邻域内, 提高系统抗干扰能力且改善系统输出特性。
1 算法描述考虑一类存在未知时变干扰的单输入单输出线性离散系统
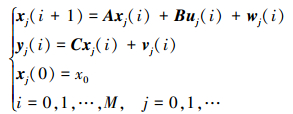
|
(1) |
式中,xj∈Rn, uj∈R和yj∈R分别是状态向量、输入向量和输出向量, wj(i)∈Rn和vj(i)∈R是非周期性未知时变状态扰动和输出干扰, A, B, C是相应维数的实数矩阵且C*B为实数, x0是系统初始状态, j表示第j次迭代次数, M表示一次迭代的离散采样总点数, i∈[0, M]表示一次迭代中的第i个离散点。此处假设输出期望轨迹yd(i)已知, CB≠0。
假设系统期望轨迹yd(i)已知, 且随着迭代次数的增加, 系统输出逼近期望轨迹, 即
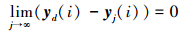
|
(2) |
式中,i=1, 2, …, M。
为了有效抑制系统干扰, 在ILC算法中引入遗忘因子来进行扰动抑制。本文以开环PID型带遗忘因子ILC算法进行系统控制, 具体迭代学习律如下
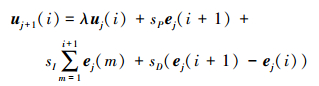
|
(3) |
式中
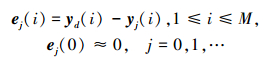
|
(4) |
式中,0<λ<1是遗忘因子, sP, sI, sD是迭代学习算法的实数控制增益。
2 算法收敛性分析假设1 理想情况下, 状态扰动和输出干扰被完全抑制, 此时存在期望方程为
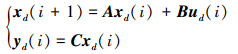
|
(5) |
假设2 系统状态扰动和输出扰动有界, 即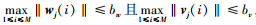
定理1 系统(1)在迭代学习律式(3)的作用下, 如果满足
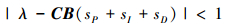
|
(6) |
则系统输出有界, 算法收敛。
证明 定义矩阵Y(j), U(j), Yd, E(j), W(j), V(j)如下
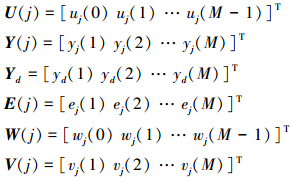
|
(7) |
式中,T表示转置, E(j)=Yd-Y(j)。
定义a∈RM, ψ∈RM×M如下
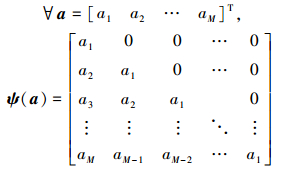
|
(8) |
因此算子ψ是一个关于a的下三角Toeplitz矩阵。可定义
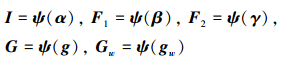
|
(9) |
式中
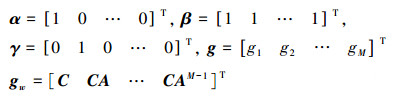
|
(10) |
式中
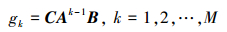
|
(11) |
可由(1)式推导得
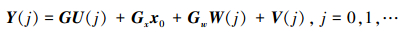
|
(12) |
式中
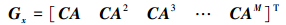
|
(13) |
由于系统扰动和输出干扰是非周期随机干扰, 因此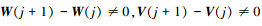
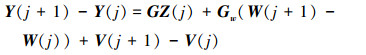
|
(14) |
式中
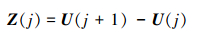
|
(15) |
可知
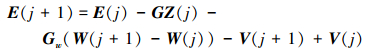
|
(16) |
根据以上定义, 可推得下式
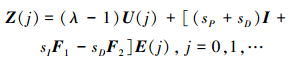
|
(17) |
(17) 式代入(16)式可得
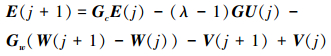
|
(18) |
式中
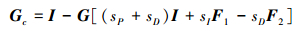
|
(19) |
将(12)式代入(18)式, 可得
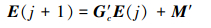
|
(20) |
式中
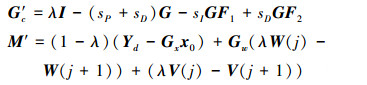
|
(21) |
此时, 根据(8)式可定义
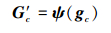
|
(22) |
式中
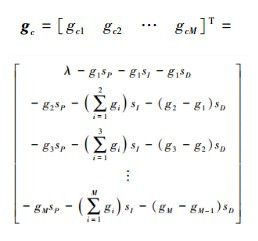
|
(23) |
与参考文献[14]相比, (20)式中向量E(j+1)的一般表达式发生了变化, 此时使用矩阵理论中的迭代定理[22]进行重新分析, 具体如下:
定理2 设A=L-N∈Rn×n非奇异, b∈Rn, 如果L非奇异且L-1N的谱半径满足ρ(L-1N)<1, 则对任何初始向量x(0), 由Lx(k+1)=Nx(k)+b产生的迭代序列{x(k)}收敛到解x=A-1b。
由于系统状态扰动及输出干扰为未知非周期时变信号, 由(21)式可知, M′与系统状态参数及相邻2次的扰动信号差值有关, 与输出误差E(j)无关。合理的λ取值可以有效减小M′, 达到系统干扰抑制的作用。同时, 由定理2知, M′不影响E(j)的收敛性但会影响迭代序列的收敛解, 当M′≠0且ρ(G′c)<1时, (20)式的收敛解为
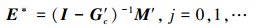
|
(24) |
从定理2及(20)式可知E(j)收敛性仍然由G′c决定, 此时G′c作为下三角矩阵收敛的充要条件为特征值必须全部位于单位圆内, 由于g1, λ及控制增益为实数, 因此带遗忘因子的ILC算法收敛充要条件可简化为
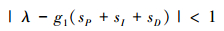
|
(25) |
即可证得。
由(25)式可知

|
(26) |
可知遗忘因子将导致控制增益取值区间整体发生平移, 但取值区间长度不变。但是与参考文献[15]相比, 系统收敛条件明显放宽, 对于系统状态矩阵参数的要求明显降低。
3 单调收敛条件和最优控制增益 3.1 单调收敛条件由定理1可知, 满足(6)式的条件时系统(1)输出误差收敛且输出有界。但是要实现算法单调收敛, 需要满足以下条件[13]
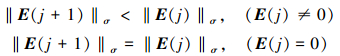
|
(27) |
式中,σ=1, 2, ∞, j=0, 1, …。
引理1 基于遗忘因子的ILC算法单调收敛的条件是
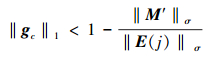
|
(28) |
证明 根据(20)式及范数性质, 可得
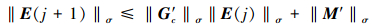
|
(29) |
当║M′║σ=0时, G′c满足下式时算法单调收敛
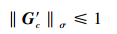
|
(30) |
当║M′║σ>0时, (29)式可变为
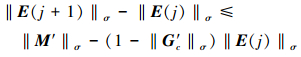
|
(31) |
若满足
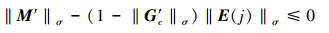
|
(32) |
即
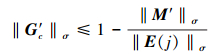
|
(33) |
则(27)式成立, 算法单调收敛。
综合(30)式与(33)式, 可知(33)式成立时, 算法即单调收敛。
由于G′c是一个下三角Toeplitz矩阵, 可知
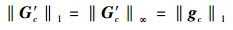
|
(34) |
由于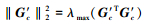
则

|
(35) |
因此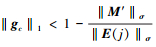
注1 由(33)式可知, 当M′≠0时, 为实现系统单调收敛, ║G′c║σ的取值上限实际上是随着║E(j)║σ的减小而减小的, 当E(j)→E*时, ║G′c║σ取值上限达到最小值, 此时满足(33)式条件的G′c才可以真正实现算法单调收敛。同时也能得到结论:当系统中存在非严格重复扰动时, 能够实现算法单调收敛的控制增益取值范围实际上在变小。
3.2 最优控制增益ILC控制系统单调收敛时最优控制增益问题可转换为求║G′c║σ最小值问题[13-14], 因此最优控制增益问题转变为min(║gc║1)问题。具体如下
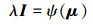
|
(36) |
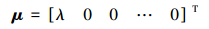
|
(37) |
则gc=μ-QS, 其中S∈R3, Q∈RM×3, S=[sP sI sD]T, 且
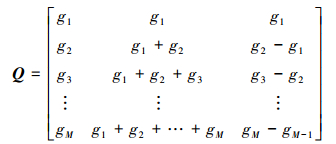
|
(38) |
由于
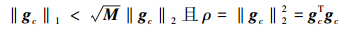
|
(39) |
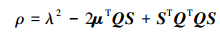
|
(40) |
通过对ρ中的S求梯度, 并令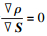
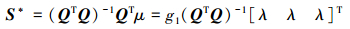
|
(41) |
假设

|
(42) |
可得最优控制增益值为
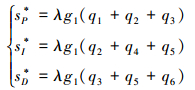
|
(43) |
由(43)式可知, 当系统状态方程参数确定后, ILC算法的最优控制增益也随之确定。当ILC算法中引入遗忘因子后, 迭代学习律(3)的最优控制增益值随遗忘因子值变化而变化。
4 仿真验证以文献[14]中仿真示例为仿真对象, 使用文献[23]中的严格非重复扰动, 可得
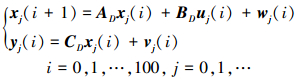
|
(44) |
式中
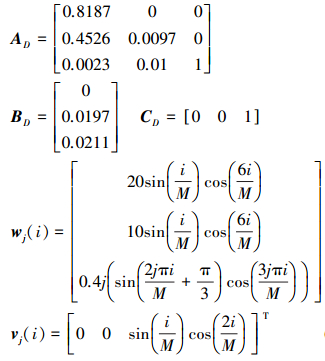
|
(45) |
采样时间为T=0.01 s, 迭代周期tf=1 s
期待输出轨迹为
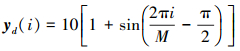
|
(46) |
式中,sP=-0.098 8。
此时传统PID型ILC算法最优增益为

|
(47) |
引入遗忘因子sP*=-0.088 9时, 由(43)式计算可得
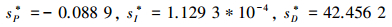
|
(48) |
为对比不同控制增益下算法收敛特性, 假设带遗忘因子的ILC算法使用(47)式所示控制增益时系统输出误差为e1, 使用式(48)所示控制增益时系统输出误差为e2, 最后一次迭代时系统输出误差范数为min(norm(e1))和min(norm(e2)), 则对应的输出误差范数如图 1所示。
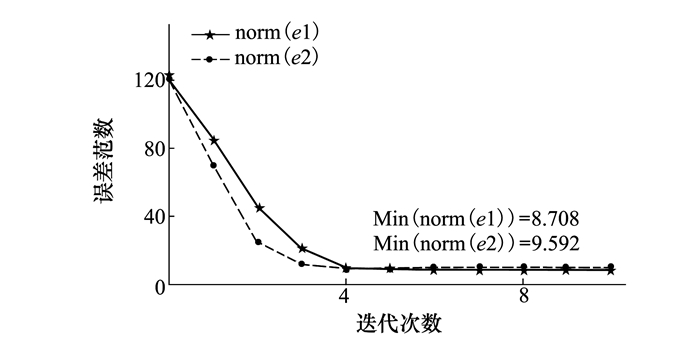
|
| 图 1 不同增益时输出误差范数对比 |
由图 1可知, 改进的控制增益可以使系统在经历3次迭代后基本达到最小值, 而传统最优控制增益需要4次迭代后趋于稳定值, 收敛速度明显提升。
当系统迭代4次后, 不同控制增益的ILC算法基本都实现了快速收敛, 达到了最小系统输出跟踪误差。为对比不同控制增益对系统输出误差波动的抑制能力, 选择第4次迭代到第20次迭代共17次迭代的输出误差范数的方差进行对比, 如表 1所示:
由表 1可知, 迭代学习从第4次至第20次时, 使用传统增益的带遗忘因子ILC算法输出跟踪误差波动较大, 而本文提出的新最优控制增益可以有效减小时变干扰引起的输出跟踪误差波动。
下面分析遗忘因子对随机干扰的抑制作用, 假设当迭代次数j=10时系统扰动幅值达到最大且存在随机干扰, 此时
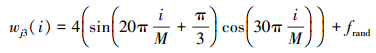
|
(49) |
式中,frand表示幅值为1的随机干扰。当遗忘因子λ=0.9时输出误差范数如图 2所示。
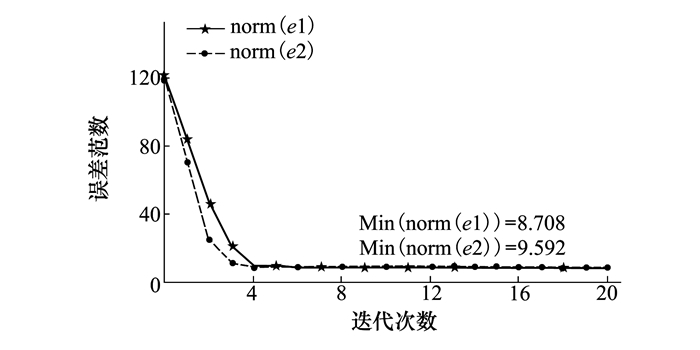
|
| 图 2 随机干扰时不同控制增益输出误差范数对比 |
由图 2可知, 本文提出的新最优控制增益ILC算法仍然有效抑制随机干扰造成的系统跟踪误差, 保证系统快速收敛且收敛速度较快。
继续使用输出误差范数的方差来对比不同算法控制增益对系统输出跟踪误差波动的抑制作用, 具体如表 2所示:
由表 2可知, 当系统中随机干扰为主要干扰时, 本文提出的最优控制增益对随机干扰引起的输出跟踪误差波动有明显的抑制作用, 且优于传统最优控制增益算法。
5 结论本文针对一类含非严格重复干扰的LTI系统, 提出了一种带遗忘因子ILC算法的最优控制增益设计方法。该方法扩展了带遗忘因子ILC算法的收敛充要条件, 得到了算法最优控制增益, 证明了该算法在快速收敛的同时保证输出跟踪误差收敛到零的邻域内。同时依据遗忘因子和系统状态方程参数可快速计算出系统最优控制增益, 实现系统单调快速收敛, 抑制系统非严格时变扰动对系统输出的影响, 兼顾了系统收敛性和抗干扰性。
与传统最优控制增益设计方法相比, 文中所提方法充分考虑了遗忘因子对算法收敛性及算法控制增益值的影响, 为时变遗忘因子ILC算法及自适应遗忘因子ILC算法的最优控制提供了理论依据。同时, 对于一类如直线电机的复杂非线性系统来说, 通常都是简化为含复杂扰动的线性系统进行分析与研究, 本文也为该类系统的精密运动控制提供了新的研究思路。
| [1] |
刘金琨. 智能控制[M]. 3版. 北京: 电子工业出版社, 2014.
LIU Jinkun. Intelligent Control[M]. Third Edition. Beijing: Publishing House of Electronics industry, 2014. (in Chinese) |
| [2] | HU K, OTT C, LEE D. Online Iterative Learning Control of Zero-Moment Point for Biped Walking Stabilization[C]//2015 IEEE International Conference on Robotics and Automation, Seattle, 2015: 5127-5133 https://www.researchgate.net/publication/283129685_Online_iterative_learning_control_of_zero-moment_point_for_biped_walking_stabilization?_sg=jNKj-aSU4m_a3zHfE6slC18twmgu24X4jrfvF0oDZoTJ08XEKT0wPJI01Ww1r8JMcFntJ4Focwkk1Q4PAgWvCg |
| [3] | CHIEN C J, HUNG Y C, CHI R H. Design and Analysis of Current Error Based Sampled-Data ILC with Application to Position Tracking Control of DC Motors[C]//2014 11th IEEE International Conference on Control & Automation, Taichung, 2014: 1162-1167 |
| [4] | LI W S, ZHANG J, LI Y. A Simpler and More Efficient Iterative Learning Controller for PMSM Torque Ripple Reduction[C]//2013 IEEE International Conference on the Electrical Machines and Systems, Busan, 2013: 1231-1235 https://www.researchgate.net/publication/261378378_A_simpler_and_more_efficient_iterative_learning_controller_for_PMSM_torque_ripple_reduction |
| [5] |
姜晓明, 陈兴林. 有限长迭代学习控制及在扫描光刻中的应用[J]. 电机与控制学报, 2014, 18(9): 80-86.
JIANG Xiaoming, CHEN Xinglin. Finite Iterative Learning Control and Its Application to Wafer Scanner System[J]. Electric Machines and Control, 2014, 18(9): 80-86. (in Chinese) DOI:10.3969/j.issn.1007-449X.2014.09.013 |
| [6] |
李奇军.直线电机垂直驱动系统在数控珩磨机中的应用研究[D].兰州: 兰州理工大学, 2014 LI Qijun. Research on the Application of Linear Motor Vertical Driver System in the CNC Honing Machine[D]. Lanzhou, Lanzhou University of Technology, 2014(in Chinese) |
| [7] | OWENS D H, FENG K. Parameter Optimization in Iterative Learning Control[J]. International Journal of Control, 2003, 76(11): 1059-1069. DOI:10.1080/0020717031000121410 |
| [8] | HARTE T J, HÄTÖNEN J, OWENS D H. Discrete-Time Inverse Model-Based Iterative Learning Control:Stability, Monotonicity and Robustness[J]. International Journal of Control, 2005, 78(8): 577-586. DOI:10.1080/00207170500111606 |
| [9] | OWENS D H, HÄTÖNEN J, DALEY S. Robust Monotone Gradient-Based Discrete-Time Iterative Learning Control[J]. International Journal of Robust and Nonlinear Control, 2009, 19(6): 634-661. DOI:10.1002/rnc.1338 |
| [10] | OWENS D H. Multivariable Norm Optimal and Parameter Optimal Iterative Learning Control:a Unified Formulation[J]. International Journal of Control, 2012, 85(8): 1010-1025. DOI:10.1080/00207179.2012.673136 |
| [11] | STEFAN H, MADHUKAR P. An iterative Learning Controller with Reduced Sampling Rate for Plants with Variations of Initial States[J]. International Journal of Control, 2000, 73(10): 882-889. DOI:10.1080/002071700405860 |
| [12] | HATZIKOS V, HÄTÖNEN J, OWENS D H. Genetic Algorithms in Norm-Optimal Linear and Non-Linear Iterative Learning Control[J]. International Journal of Control, 2004, 77(2): 188-197. DOI:10.1080/00207170310001649351 |
| [13] | MADADY A. PID Type Iterative Learning Control with Optimal Gains[J]. International Journal of Control, Automation, and Systems, 2008, 6(2): 194-203. |
| [14] | MADADY A. An Extended PID Type Iterative Learning Control[J]. International Journal of Control, Automation and Systems, 2013, 11(3): 470-481. DOI:10.1007/s12555-012-0350-4 |
| [15] |
傅勤. 基于Jacobi方法的线性离散时间系统的迭代学习控制[J]. 控制理论与应用, 2015, 32(1): 122-126.
FU Qin. Iterative Learning Control for Linear Discrete-Time Systems Based on Jacobi Method[J]. Control Theory & Applications, 2015, 32(1): 122-126. (in Chinese) |
| [16] |
兰天一, 林辉. Lebesgue-p范数意义下区间可调节的变增益加速迭代学习控制[J]. 控制与决策, 2017, 32(11): 2071-2075.
LAN Tianyi, LIN Hui. Accelerated Iterative Learning Control Algorithm with Variable Gain and Adjustment of Interval in Sense of Lebesgue-p Norm[J]. Control and Decision, 2017, 32(11): 2071-2075. (in Chinese) |
| [17] |
曹伟, 戴学丰, 刘艳菊. 移动机器人的可变遗忘因子离散迭代学习控制[J]. 北京工业大学学报, 2015, 41(10): 1516-1521.
CAO Wei, DAI Xuefeng, LIU Yanju. Discrete Iterative Learning Control with Variable Forgetting Factor for Mobile Robots[J]. Journal of Beijing University of Technology, 2015, 41(10): 1516-1521. (in Chinese) DOI:10.11936/bjutxb2014100068 |
| [18] |
汪首坤, 彭建敏. 带遗忘因子的预测迭代学习控制在阀控非对称缸系统中的应用研究[J]. 机械工程学报, 2014, 50(10): 191-198.
WANG Shoukun, PENG Jianmin. Forecast Iterative Learning Control with Forgetting Factor and Its Application in Valve-Controlled Asymmetric Cylinder[J]. Journal of Mechanical Engineering, 2014, 50(10): 191-198. (in Chinese) |
| [19] | WANG H B, DONG J, WANG Y L. High Order Feedback-Feedforward Iterative Learning Control Scheme with a Variable Forgetting Factor[J]. International Journal of Advanced Robotic Systems, 2016, 13(3): 95. DOI:10.5772/63936 |
| [20] | CHIANG J, LIU J S. A P-type Iterative Learning Controller for Robust Output Tracking of Nonlinear Time-Varying Systems[J]. International Journal of Control, 1996, 64(2): 319-334. DOI:10.1080/00207179608921630 |
| [21] | CAO Z X, DVRR H B, EBENBAUER C, et al. Iterative Learning and Extremum Seeking for Repetitive Time-Varying Mappings[J]. IEEE Trans on Automatic Control, 2017, 62(7): 3339-3353. DOI:10.1109/TAC.2016.2633724 |
| [22] |
GOLUB G H, VAN LOAN C F.矩阵计算[M].袁亚湘, 译.北京: 人民邮电出版社, 2011 GOLUB G H, VAN LOAN C F. Matrix Computations[M]. YUAN Yaxiang, Translator. Beijing, Posts & Telecom Press, 2011(in Chinese) |
| [23] |
吕庆, 方勇纯, 任逍. 含非严格重复扰动的抗扰迭代学习控制[J]. 控制理论与应用, 2014, 31(9): 1190-1197.
LYU Qing, FANG Yongchun, REN Xiao. Anti-Disturbance Iterative Learning Control for Nonlinear Systems with Time-iteration-varying Disturbances[J]. Control Theory & Applications, 2014, 31(9): 1190-1197. (in Chinese) |


