随着无人机飞行包络的拓展和任务的多样化, 飞行器目标任务、环境的变化以及空间未建模动态和复杂非线性因素等都影响着飞行的稳定性。飞行控制系统在处理这些不确定条件时, 基于传统稳定跟踪的方法均有可能出现无法应对复杂情况而导致飞行器失稳的情况。而单纯的故障重构只用于解决器件故障情况, 无法有效处理由于大范围不确定和突发干扰带来的控制器失稳问题。因此需要研究闭环系统稳定性预测度量方法, 实现多故障、大范围不确定的闭环控制系统失稳分析, 为后续的重构策略提供决策信息。
文献[1-3]实现了对于系统干扰和不确定的具有鲁棒性的观测器, 用于进行非线性不确定系统的故障检测。然而这种方法对于大范围不确定和干扰带来的性能变化难以应对,这就使得基于对象模型或数据实现控制系统的稳定性能预测变得至关重要。文献[4]介绍了故障检测、隔离和系统重构(FDIR)方法技术方法的发展趋势,文献[5]针对具体航空器实现了基于控制性能度量和修正控制目标的控制重构方法。
随着近年相空间重构应用领域推广和神经网络技术的发展, 针对此类非线性系统采用相空间重构的方式揭示其状态变化机理的方法得到重视。文献[6-7]基于相空间重构理论, 采用核函数的方式构建非线性系统动力学模型。但未研究模型的后续行为预测和判定, 且其应用场景为随机非线性系统, 与本文需要解决的应用问题存在差异。
为了有效解决存在故障和不确定条件下的无人飞行控制系统的控制性能分析问题, 针对包含各类非线性环节、时滞以及混沌效应的非线性系统完整推导了鲁里叶系统的状态稳定条件, 给出了非线性鲁里叶系统失稳的诱因,采用相空间重构理论, 基于多模态核函数进行了非线性鲁里叶系统的预测模型构建。在此基础上, 通过状态的变迁趋势实现非线性系统稳定性的预测度量, 可有效应对同时具有故障和大范围不确定的非线性闭环系统的失稳判定, 综合解决多故障和不确定性带来的控制器失稳检测。
1 鲁里叶系统的失稳机理分析在无人机飞行过程中, 自身的设备故障, 外部环境改变以及大机动的指令都有可能诱发飞行器的控制失稳。为了有效说明系统稳定性的影响因素, 构建其基本的运动方程。
针对一般高速面对称无人飞行器的特性, 考虑明显的非线性、耦合和不确定特性,其绕心的一般非线性运动方程可写为
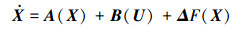
|
(1) |
式中, X=[α, β, γv, ωz, ωy, ωx]表示状态变量, U=[δz, δy, δx]表示控制变量。ΔF(X)=DΔ(t)E表示状态引起的结构性不确定性。其中D和E分别是已知的常数矩阵, 表示不确定性的结构, Δ(t)为未知有界的不确定性参数或矩阵, 表示在不确定性结构下的有界时变摄动。
定理1 对于系统(1), 基于鲁棒控制中的小增益理论, 若存在连续的C阵为单位对角阵的输出反馈控制, 则闭环系统稳定的充分必要条件是
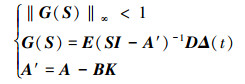
|
(2) |
式中,G(S)为系统闭环传函数, A′为闭环后系统的状态矩阵, K为反馈增益矩阵。
那么闭环后系统的矩阵A′为渐近稳定。且存在非负定矩阵P≥0, 满足下述矩阵不等式(LMI)
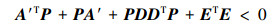
|
(3) |
该定理可通过小增益理论和线性矩阵不等式(LMI)易证。若系统(1)满足上述定理, 则通过反馈回路, 使得闭环后的系统满足一般渐进稳定特性。
不失一般性, 考虑到鲁里叶非线性系统的特性, 典型的控制器一般可表征为输出反馈形式, 控制量可描述为
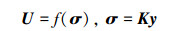
|
(4) |
式中, 函数f(σ)连续可导, 且满足f(0)=0。则系统(1)为包含不确定的直接鲁里叶系统。
针对(4)式, 针对系统进行线性化处理, 忽略二阶以上的非线性项, 则可得
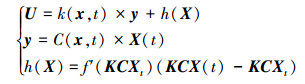
|
(5) |
式中, 等式后第一项表示线性反馈项, 第二项表征非线性的前馈或反馈项, 其可写为相对于状态的一阶导数相关项。
可得系统闭环后的方程为
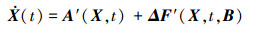
|
(6) |
式中, ΔF(X, t)描述不确定项, 表征为加法的不确定性形式。则闭环后的稳定系统可由一个稳定的自治系统加由控制器非线性引起的不确定项构成。
为使系统(6)稳定, 基于采用鲁里叶特性的闭环系统, 直接采用LMI(线性矩阵不等式)方法进行分析。当控制器包含非线性环节后, 考虑一定范围的对象不确定性, 闭环系统也可能由不确定项诱发失稳。可能存在的失稳诱因包括:故障引起的不完全可控, 系统与伺服机构不确定项(包括耦合不确定项和模型特性变化等因素)以及控制器本身不确定非线性。
定理2 基于包含鲁里叶特性的不确定非线性系统(6), 若在确定特征点存在

|
(7) |
则系统闭环渐进稳定的充分必要条件是
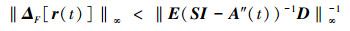
|
(8) |
基于上述定理, 根据控制理论中的稳定半径概念和小增益原理, 当A″(t)为渐进稳定矩阵时, 不确定项的稳定范围应该为

|
(9) |
当系统结构的不确定性的幅值超过一定范围时, 则原有的闭环系统会失稳。而该范围可被定义为鲁棒性中的稳定半径。
当存在作动器和传感器故障时, 考虑到故障类型。当编号为j的作动器故障时, 故障模型可表征如下
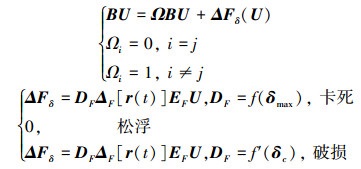
|
(10) |
系统方程附加B阵的常系数矩阵Ω与控制变量相关的不确定项构成。
同样, 针对传感器故障, 当编号j的传感器故障时, 考虑可见的传感器故障包括大噪声以及断路, 在不改变C阵的情况下, 增加附加系数矩阵, 以及可见不确定性偏差项。
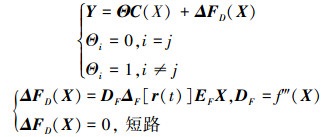
|
(11) |
定理3 对于存在伺服和传感器故障的增广系统模型
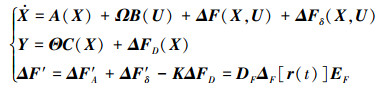
|
(12) |
若状态变量阶次为n, 且C(X)为对角元素为xi的对角阵。则系统输出反馈稳定的条件是:
1) 矩阵Π=Ω×Θ秩为n;
2) 当存在输出反馈U=-K·Y
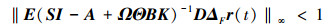
|
3) 当存在输出反馈U=-K·Y
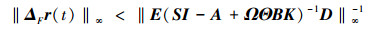
|
(13) |
其中(1)为系统输出反馈稳定的必要条件, (2)、(3)为系统输出反馈稳定的充分条件。
从上述分析可见, 由于引起鲁里叶非线性系统失稳的原因除了信号可测的器件故障外, 多种类型的不确定性也容易破坏原有系统稳定性。原有基于模型的分析方法计算复杂且无法处理故障和不确定情况,为了在线快速判定飞行器的稳定状态,直接采用基于数据序列实现鲁里叶非线性系统稳定性的预测分析。
2 基于时间序列的失稳判据分析通过对飞行器的输入输出数据进行时间序列分析和逼近基元模型建模, 得到的飞行器的辨识模型。当飞行器受到不确定性条件的影响——如舵故障或气动拉偏时, 飞行器的状态输出与控制输入相较正常状态必然有所不同, 由此引起所建辨识模型的逼近基元的迁移态发生变化。那么通过对基元迁移特性的分析, 便可以进行系统稳定性的判别, 并基于一定时序基准下的状态欧式空间距离范数可以度量其失稳的程度。为复杂非线性鲁里叶系统的稳定性分析提供了一种新的实现思路。
复杂的非线性鲁里叶系统包含了连续与离散环节, 其状态变化呈现出一定的混沌特性。而基于时间序列数据的相空间重构理论以及非线性系统逼近基元模型方法可将复杂非线性系统的状态空间动力学映射到逼近基元空间中, 为统一快速评价非线性系统稳定性提供可能。
基于著名的Stone-Weierstrass定理和多层神经网络对连续函数逼近特性的相关结论, 采用基于核函数的逼近基元模型可连续逼近任意连续非线性系统。但闭环后系统包含了连续的弹体与离散的控制器, 且控制器中存在多种时滞与非线性特性。无法直接得到精确闭环离散数学模型。需要基于现有非线性系统逼近基元模型稳定性分析方法进行包含离散环节的闭环系统稳定性的拓展推导。
对于一般的连续非线性系统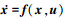
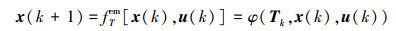
|
(14) |
由于非线性, 一般无法得到上式的闭合形式, 采用近似Euler方法, 则可以得到系统的Euler近似离散时间模型如下
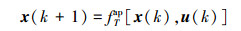
|
(15) |
则有以下引理成立:
引理1 考虑非线性对象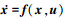
1) 存在函数ρ∈k∞, 常数T1*>0, 当T∈(0, T1*)时, 对任意x∈Rn, 近似模型的误差满足
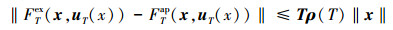
|
(16) |
2) 存在常数T2*>0, L1>0, 当T∈(0, T2*)时, 对于任意x, y∈Rn, 有
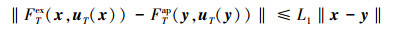
|
(17) |
3) 闭环精确模型全局指数稳定。
基于上述引理, 闭环后的近似时间离散方程稳定性等价于闭环后原有连续离散混合系统的稳定性。
为了有效进行系统状态的稳定性判定, 首先须完成预测模型的构建。将多维的近似离散系统映射为低维的多维核函数逼近基元模型。那么系统观测值的时间序列如下所示
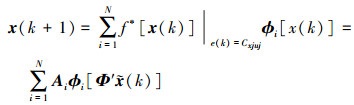
|
(18) |
式中, x(k+1)表示k+1时刻的状态值, 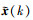
引理2 对于(18)式欧拉近似离散时间方程和方程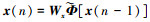
1) 存在函数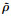
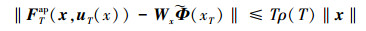
|
(19) |
2) 存在常数T4*>0, L2>0, 当T∈(0, T4*)时, 对于任意x, y∈Rn, 有

|
(20) |
对于(15)式给出Euler近似离散方程, 设控制量一般描述为
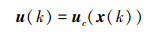
|
(21) |
带入(15)式, 可得闭环递推方程为
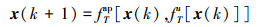
|
(22) |
该方程为典型非线性泛函系统, 在采样时刻, 当控制量在相邻时刻之间不变时, 基于(18)式和Stone-Weierstrass定理, 易证明
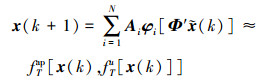
|
(23) |
则有引理2中1)条件成立。该逼近定理表征了自回归网络与齐次非线性系统状态输出的一致性。
对于引理2中的条件2), 取x=y+Δy, 基于近似欧拉方程, 可得

|
(24) |
由引理2条件2)左式可得
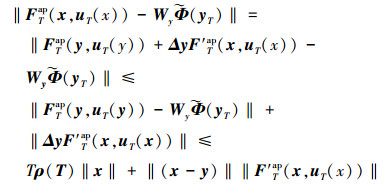
|
(25) |
取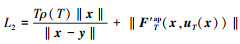
则有引理2中条件2成立。
基于以上推导, 对于定义在n维欧式空间的非线性闭环系统, 如(14)式所示, 其稳定性等价于(18)式给出的逼近模型
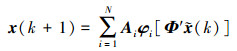
|
(26) |
状态迁移过程中, 系统应该具有同构特征[9], 因此网络结构被定义为主成分加自回归形式, 则可以迭代利用主要变量进行快速模型泛化处理。通过分析(26)式的稳定性, 则可以给出原有混合连续离散系统的稳定性。
基于(26)式中的基元模型形式的确定, 使用RBF神经网络对系统模型进行非线性回归模型的构建, 设计了q高斯函数作为径向基函数, 形式如下
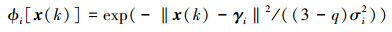
|
(27) |
式中, 变化的q值为非广延熵指数, σi为宽展度, γi为隐单元的中心点。对于采用q高斯函数作为径向基函数的逼近模型, 基于高斯近似离散模型进行被控对象的状态自回归预测模型构建[10-12]。
采用q高斯分布的中心核函数, 为加速在线的计算过程, 本文提出了带有自适应基函数的遗忘因子η。
核心基元采用主成分确定, 则基元模型的确定即转化为参数确定问题, 根据所采用的核函数, 所需要进行优化和求解的问题如(28)式所示
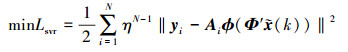
|
(28) |
式中,A=(a1, …, am)表示权系数, yi=(yi1, …yim)T表示模型的输出预测集合。考虑到算法收敛速度、样本的时序更新、观测数据的噪声等影响到核函数的泛化能力的因素[13], 确认基础核函数, 采用基于误差反馈的改进(q优化)优化解方法进行参数的求解[14]。
基于(28)式, 对q高斯核函数进行梯度计算, 在假设q值确定的条件下, 基于(26)式对核函数进行参数的梯度求解, 分别对核函数的中心点、权重、基元宽度求偏导得
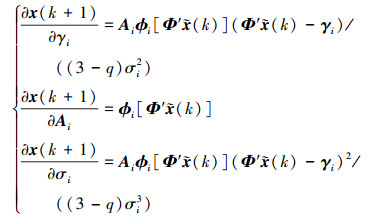
|
(29) |
获取偏导后, 对(28)式, 采用搜索方法确定相关参数。步长的确定依据基本的Armijo准则[15], 得到的迭代求解量为
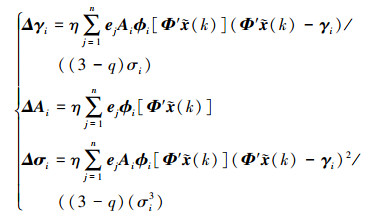
|
(30) |
式中, η位于[0, 1]为遗忘因子, 可消除之前数据的影响, ej表示步长。等同于下文中的t值。根据(28)式的截止条件, 参数的搜索准则定义为
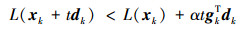
|
(31) |
式中, 参数xk表示被优化的参数, dk为该参数的梯度方向, t表示步长, α为0至0.5之间的常数, gkT=▽L(xk)。
考虑到需要优化的参数为3个, 且参数q(非指数广义熵)直接影响到高斯基元函数的分布特性。为了提升预测函数的泛化能力, 需要自适应调整q值适应不同的阶段。算法定义如下:
step1 初始化网络, 设定3个参数初值, 初始化公式如下
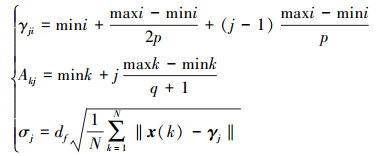
|
(32) |
式中,i,j,k分别代表输入, 隐单元和输出, q是输出维数, p是隐单元数, N是训练数据量, df是宽度调节系数。
然后引入一个窗口区间的IO数据, 设定最大迭代次数、遗忘因子和训练误差。
step2 自适应调整q值, q值得取值空间设为(0, 3), 从大于零的小值ε开始进行迭代。进行迭代。
step3 设t=1:T, 基于确定的ε进行网络参数优化, 根据(32)式计算计算权重Ai, 根据(26)式计算网络实际输出, 在根据(28)式计算指标。
step4 如果计算结果满足指标, 则跳出, 否则根据(31)式进行调整, 支持满足指标为止。
step5 对于q值, 采用并行处理方式, 各分值分别取空间(0, 1), 1, (1, 3), 当出现中间条件时, q值进行区域变化。每次出发q值区域选择的条件为

|
通过以上方式, 容易得到一定窗口内的闭环预测模型, 由于采用了q高斯函数, 其收敛性证明可以采用新方式进行。也可以证明其可能的跟进性。
通过以上方法, 在获取到闭环预测模型后, 则可基于该模型进行系统状态的变迁过程分析, 从而确定稳定态、动态自主稳定态以及发散态, 从而为线上基于数据的快速稳定性分析奠定基础。
由于基础的基元被定义为由xiq确定的逼近基元状态空间。以此为基础建立逼近基元空间的转移模型。
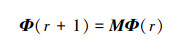
|
(33) |
式中
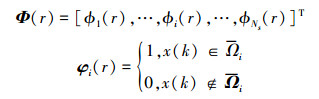
|
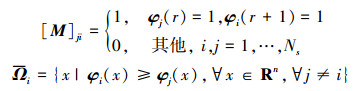
|
(34) |
式中, φi(r)表示系统在逼近基元空间中第r步转移后, 系统状态位于第i个逼近基元感受野的可能性。[M]ji表示系统状态由逼近基元φi的中心点出发, 在有限视场转移到逼近基元φj的可能性。Ωi称为第i个逼近基空间强感受野(域)。ϕi(x)被称为距离第i个基空间的野值。根据转移模型, 采用基准的李亚普诺夫稳定定理则可以直接判定闭环系统状态的稳定性。
引理3 对于系统(26), 若存在(34)式所示的状态转移矩阵M′的某个子块Mi, 总存在s>0使得Mir+s=Mir成立, 则有:
1) 当Mir ≠0, s>1时, 子块Mi中逼近基元组成的区域动态稳定基空间;
2) 当Mir ≠0, s=1时, 子块Mi中逼近基元组成连通的封闭区域, 该基元空间为稳定基;
3) 对于某逼近基元空间φbi感受野中覆盖的基元φj关于平衡空间φe是稳定的, 则φbi关于φe稳定水平记为
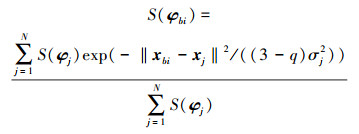
|
(35) |
若该值大于λ, 且满足Mbir ≠0, s=1, 则称系统以λ水平渐进稳定。
针对模型基元的移动路径计算, 即转移矩阵[M]ji, 则可以获取到针对典型模态下定常非线性系统的基本基元空间构成以及转移特性。其该算法可描述为:
1) 基于(26)式中的基元空间, 计算矩阵[M]ji;
2) 选择某给定子块Mi, 搜寻是否存在s, 满足Mir+s=Mir, 不成立继续执行, 否则进入下一步;
3) 若s>1, 该子块对应基元空间为动态稳定基元空间, 该基元空间为动态稳定基元φde。否则执行下一步;
4) 获取该基元, 该基元为稳定基元φe。
5) 计算每个基元关于平衡基元φe的稳定水平δ(φj);
6) 根据逼近基元φbi和感受σj, 根据基元之间的欧式范数计算覆盖范围, 并基(35)式计算稳定水平λ。
至此, 根据典型模态下的闭环离散非线性方程得到系统的基准转移态。可根据在线的方式动态计算系统稳定性。
根据基础转移矩阵以及逼近基元模型, 当实时获取到系统的输出时, 需要针对性设计状态观测器获得系统的真实状态值, 然后根据基元空间获取其处于哪个基元空间的最强感受野范围。
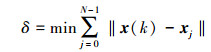
|
(36) |
获取该基元的稳定水平, 则直接获取系统此时的量化稳定值。通过合理的σ选择, 则保证系统任意状态均处于不同基元空间的感受野中。在实时分析中, 通过直接一步的计算即可进行稳定性的判定。
通过以上方法, 当闭环系统以期望性能运行时, 其遵循已有的基元转移方式, 当存在大范围不确定性以及器件故障导致状态发生突变时, 基于理想状态转移进行稳定程度的判定, 一旦系统状态位于发散基元空间的感受域内, 则说明正常系统无法保持其稳定, 系统失稳。而通过对于稳定水平λ的阈值设置, 失稳决策系统可在处于边界状态时启动系统重构。
3 应用分析针对飞行控制器的失稳判定, 以典型滑翔飞行器为例, 通过对典型失稳诱因的分析实现基于数据的在线稳定性分析判定分析。
取飞行器的稳定纵向控制器, 以巡航飞行为典型状态, 分别计算其在巡航阶段的特性。首先采用自组织网络进行正常状态下的逼近分析。
选取马赫数为4、高度30 km的巡航飞行状态, 直接获取系统的状态输出曲线。可以得到姿态角的三轴变化率。
以该状态作为网络输入, 获取系统的预测输出, 采用上文中所用方法, 分析飞行器某时刻的稳定性水平。
设定典型的无人机对象以及控制器, 选择确定的定速巡航模态, 其被描述为非线性模型, 参数为:质量m=16 900 kg, 参考面积S=73 m2, 参考长度L=23 m, 质心系数为0.634, 转动惯量如下所示
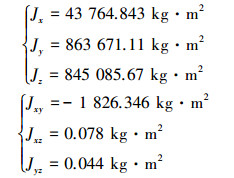
|
(37) |
控制器采用自适应控制, 结合了增益调度的思想, 应用现代鲁棒控制系统中LQR最优鲁棒调节器的设计理论, 提出LQR增益调度自适应控制方案。这种自适应控制器的结构如图 1所示:
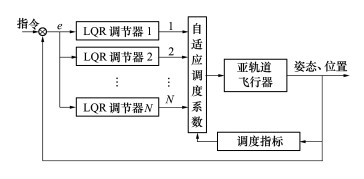
|
| 图 1 自适应控制器结构图 |
参数选取:选取25个特征点, 特征点的选择与制导律中的选择类似。在弹道平滑的区域内等距选择特征点。运动参数有剧烈变化的点都应作为特征点对待。而且在基准弹道变化剧烈的区域和弹道斜率改变符号的区域应减少特征点选取间隔。根据选取的特征点设计控制器增益。
控制器反馈矩阵Kc的计算过程与自适应制导律类似。
求解最优反馈控制率的指标函数为
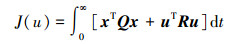
|
(38) |
利用极小值原理得到Riccati微分方程, 从该方程得到P(t), 求解得到最优控制率
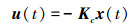
|
(39) |
式中, Kc=R-1BT(t)P(t)。
将典型无人飞行器参数及设计的自适应控制器代入, 设计飞行器模型。将不同的飞行状态偏差及飞行故障带入模型, 可得到飞行器飞行器在不同故障下的飞行状态, 使用q高斯神经网络进行拟合, 然后利用基元转移矩阵对飞行器的俯仰通道进行稳定性分析。
当飞行器处于正常巡航状态时, 使用q高斯神经网络对飞行器进行拟合。根据(27)式建立非线性逼近基元模型, 并按照2.3节所示的参数优化算法得到飞行器的神经网络逼近模型参数。
其中取数据量N=1 000, 初始化隐单元Ns=250, 遗忘因子η=0.01, 最大训练次数设为2 000次。可得拟合均方误差EMS=1.532×10-8, 拟合曲线如图 2所示,可见q高斯神经网络可以较好的拟合所建亚轨道飞行器模型。
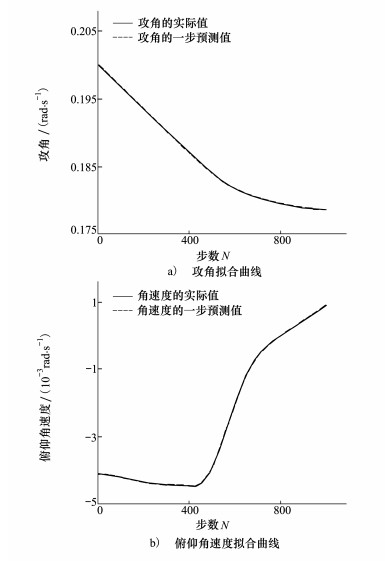
|
| 图 2 俯仰通道拟合曲线图 |
根据得到的飞行器的非线性逼近基元模型, 按照公式(33)建立逼近基元状态转移矩阵。根据公式(35), 以及3.3节所示平衡基元稳定算法, 得到系统的基准转移态。则可以得到飞行器模型在正常巡航状态下俯仰通道的渐进稳定区域如图 2所示。
根据飞行器在某时刻的状态值, 由公式(36)计算该状态处于哪个逼近基元空间的最强感受野内, 便可得到此刻飞行器的稳定度。
接下来给飞行器加入失稳诱因, 根据上文所述的步骤分析飞行器此时刻的稳定性。
1) 当存在气动拉偏时(假设拉偏为-20%), 飞行器俯仰通道的渐进稳定区域如图 4所示。
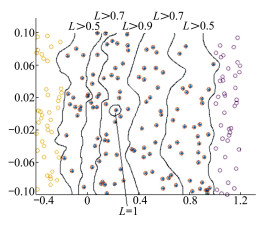
|
| 图 3 飞行器正常状态下俯仰通道稳定区域 |
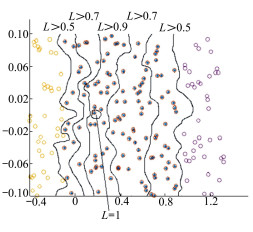
|
| 图 4 飞行器拉偏状态下俯仰通道稳定区域 |
由图 4可得, 当存在负气动拉偏时, 飞行器气动力矩减少, 其渐进稳定区域较正常飞行状态下缩小, 所以相同姿态下飞行器的稳定度较正常巡航状态降低, 飞行器稳定性下降。
2) 当存在舵故障时(假设舵效率降低为原本的50%)飞行器俯仰通道的渐进稳定区域如图 5所示。
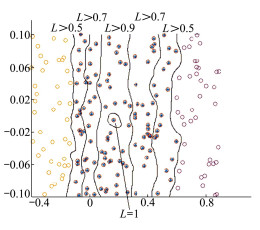
|
| 图 5 飞行器舵故障下俯仰通道稳定区域 |
由图可得, 当存在舵故障时, 飞行器纵向控制力与力矩减小, 其渐进稳定区域较正常飞行状态下缩小, 飞行器在处于大攻角情况下失稳的概率增加, 飞行器稳定性下降。
通过以上仿真实验可知, 当飞行器出现故障或者其他模型的改变时, 其基元空间也会发生改变, 从而影响相同状态量下飞行器的稳定度, 使模型失稳的可能性增加。通过设定合适的稳定性阈值, 当检测到稳定值低于该阈值时, 启动系统重构, 保障飞行器的稳定运行。
接下来就飞行器出现舵故障的情形介绍基于相空间递归网络的稳定性度量如何为系统重构提供依据。
当飞行器处于舵故障状态时, 考虑用作失稳决策的逼近基元的感受野应在数量尽可能少的前提下覆盖稳定域与发散基元的边界, 则可取系统重构的稳定度阈值为Δ=0.62, 取稳定水平λ小于0.62区间范围内的基元中心点在基元空间内的坐标和稳定水平, 如表 1所示。
| 逼近基元中心点 | 稳定水平 |
| (-0.063 2, 0.093 4) | λ=0.583 4 |
| (-0.067 7, 0.082 1) | λ=0.574 2 |
| (-0.066 3, 0.058 2) | λ=0.572 1 |
| (-0.077 1, 0.040 5) | λ=0.526 3 |
| (-0.070 4, 0.019 3) | λ=0.542 4 |
| (-0.068 2, 0.004 9) | λ=0.612 4 |
| (-0.067 2, -0.023 6) | λ=0.608 3 |
| (-0.066 1, -0.055 3) | λ=0.588 1 |
| (-0.065 8, -0.062 5) | λ=0.584 1 |
| (-0.079 1, -0.080 7) | λ=0.553 7 |
| (0.582 3, 0.078 7) | λ=0.514 8 |
| (0.553 0, 0.065 9) | λ=0.587 2 |
| (0.563 7, 0.037 0) | λ=0.515 4 |
| (0.503 6, 0.003 1) | λ=0.619 2 |
| (0.585 9, -0.036 1) | λ=0.504 1 |
| (0.564 1, -0.053 1) | λ=0.515 3 |
| (0.553 8, -0.076 9) | λ=0.520 4 |
根据(36)式计算飞行器某一状态处于哪个基元的强感受野中, 那么当飞行器处于表 1中的逼近基元的强感受野时, 飞行器失稳的的可能性大大增加, 此时便可以启动系统重构, 使飞行器保持稳定状态。
5 结论本文提出了一种基于混沌时间序列数据分析的鲁里叶系统稳定度预测度量方法。基于相空间重构理论将包含连续离散特性的非线性鲁里叶系统等价转换为近似时间离散方程, 通过在核函数中引入q高斯函数, 更好的增强了神经网络的泛化能力, 并实现了基于基元转移的稳定性分析方法。
实验表明, q高斯径向基函数可以以较高的精度完成对多输入多输出模型的拟合, 但其也存在误差下降速度慢的不足。逼近基元空间分析方法是一种由数据出发对系统进行稳定性分析的方法, 该方法为非线性系统稳定性的分析提供了一个新的平台。虽然本文进一步完善了非线性系统逼近基元模型分析法, 但仍有许多问题需要讨论, 比如平衡基元的吸引域虽然给出了稳定域大致的范围, 但稳定域边界的准确刻画仍需要进一步研究等。
| [1] | LI H, GAO Y, SHI P, et al. Observer-Based Fault Detection for Nonlinear Systems with Sensor Fault Andlimited Communication Capacity[J]. IEEE Trans on Automatic Control, 2016, 61(9): 2745-2751. DOI:10.1109/TAC.2015.2503566 |
| [2] | SERDIO F, LUGHOFER E, ZAVOIANU A C, et al. Improved Fault Detection Employing Hybrid Memetic Fuzzy Modeling and Adaptive Filters[J]. Applied Soft Computing, 2017, 51: 60-82. DOI:10.1016/j.asoc.2016.11.038 |
| [3] |
胡志坤, 孙岩, 姜斌, 等. 一种基于最优未知输入观测器的故障诊断方法[J]. 自动化学报, 2013, 39(8): 1225-1230.
HU Zhikun, SUN Yan, JIANG Bin, et al. An Optimal Unknown Input Observer Based Fault Diagnosis Method for the Drive Train System of Wind Turbine[J]. Acta Automatica Sinica, 2013, 39(8): 1225-1230. (in Chinese) |
| [4] | ZOLGHADRI A. The Challenge of Advanced Model-Based Fdir for Real-World Flight-Critical Applications[J]. Engineering Applications of Artificial Intelligence, 2018, 68: 249-259. DOI:10.1016/j.engappai.2017.10.012 |
| [5] | JUNE Chongvisal, NIKOLAS Tekles, ENRIC Xargay, et al. Talleur, Alex Kirlikk, Naira H-ovakimyan, Loss-of-Control Prediction and Prevention for NASA's Transport Class Model[C]//AIAA Guidance, Navigation, and Control Conference, National Harbor, Maryland, 2014 |
| [6] | SMITH C, JIN Y. Evolutionary Multi-Objective Generation of Recurrent Neural Network Ensembles for Time Series Prediction[J]. Neuro computing, 2014, 143: 302-311. |
| [7] | Chen T T, Lee S J. A Weighted Ls-Svm Based Learning System for Time Series Forecasting[J]. Information Sciences, 2015, 299: 99-116. DOI:10.1016/j.ins.2014.12.031 |
| [8] |
胡瑜, 陈涛. 基于CC算法的混沌吸引子的相空间重构技术[J]. 电子测量与仪器学报, 2012, 5(10): 425-430.
HU Yu, CHEN Tao. Phase-Space Reconstruction Technology of Chaotic Attractor Based on CC Method[J]. J Electron Meas Instrum, 2012, 5(10): 425-430. (in Chinese) |
| [9] |
郭小萍, 袁杰, 李元. 基于特征空间k最近邻的批次过程监视[J]. 自动化学报, 2014, 40(1): 135-142.
GUO Xiaoping, YUAN Jie, LI Yuan. Feature Space k Nearest Neighbor Based Batch Process Monitoring[J]. Acta Automatica Sinica, 2014, 40(1): 135-142. (in Chinese) |
| [10] | DENG F, GUO S, ZHOU R, et al. Sensor Multifault Diagnosis with Improved Support Vector Machines[J]. IEEE Trans on Automation Science and Engineering, 2017, 14(2): 1053-1063. DOI:10.1109/TASE.2015.2487523 |
| [11] |
韩敏, 许美玲. 一种基于误差补偿的多元混沌时间序列混合预测模型[J]. 物理学报, 2013, 62(12): 120510.
HAN Min, XU Meiling. A Hybrid Prediction Model of Multivariate Chaotic Time Series Based on Error Correction[J]. Acta Phys Sin, 2013, 62(12): 120510. (in Chinese) DOI:10.7498/aps.62.120510 |
| [12] | MUANGKOTE N, SUNAT K, CHIEWCHANWATTANA S. An Improved Grey Wolf Optimizer for Training Q-Gaussian Radial Basis Functional-Link Nets[C]//2014 International Computer Science and Engineering Conference, 2014: 209-214 |
| [13] |
李娟, 王宇平. 基于样本密度和分类误差率的增量学习矢量量化算法研究[J]. 自动化学报, 2015, 41(6): 1187-1200.
LI Juan, WANG Yuping. An Incremental Learning Vector Quantization Algorithm Based on Pattern Density and Classification Error Ratio[J]. Acta Automatica Sinica, 2015, 41(6): 1187-1200. (in Chinese) |
| [14] |
张景祥, 王士同, 邓赵红, 等. 融合异构特征的子空间迁移学习算法[J]. 自动化学报, 2014, 40(2): 236-246.
ZHANG Jingxiang, WANG Shitong, DENG Zhaohong, et al. A Subspace Transfer Learning Algorithm Integrating Heterogeneous Features[J]. Acta Automatica Sinica, 2014, 40(2): 236-246. (in Chinese) |
| [15] | AHOOKHOSH M, GHADERI S. On Efficiency of Nonmonotone Armijo-Type Line Searches[J]. Applied Mathematical Modelling, 2017, 43: 170-190. DOI:10.1016/j.apm.2016.10.055 |


