2. 西北工业大学 无人水下运载技术重点实验室, 陕西 西安 710072
试验设计是数理统计学一个重要分支, 研究如何安排试验方案, 提高试验样本分布合理性, 减小试验误差影响, 并使试验结果可以进行合理的统计分析。在工程设计优化中, 由于计算时间和计算资源的限制, 很多时候进行大量物理试验并不可行。对许多试验现象或者研究系统, 都需要采用数学模型来描述, 并用计算机模型进行数值求解或模拟。随着设计参数和约束增加, 系统的仿真模型变得非常复杂, 单次仿真需要耗费大量时间, 尤其是复杂高维非线性“黑箱”系统[1]。
为了能够在减少试验资源的同时充分揭示各个试验因素对试验结果的影响以及各因素之间的相互关系, 研究人员引入优化准则对试验样本进行优化, 提出了优化试验设计方法[2-3]。刘新亮和郭波以正交度量准则和均匀性度量准则为优化目标, 提出基于改进增强随机进化算法(enhanced stochastic evolutionary, ESE[4])的多目标优化试验设计方法[5]。刘晓路等提出一种优化拉丁方试验设计方法, 采用Cholesky方法分解获得正交性较好的拉丁方矩阵作为初始解, 通过模拟退火(simulated annealing, SA)算法对拉丁方矩阵进行优化, 确保获得的试验样本具有较好的正交性和均匀性[6]。Zhu等提出一种基于最大最小距离(maximin)准则连续局部枚举(successive local enumeration, SLE)方法, 可以使新生成的样本点与所有样本点间最小距离最大化[7]。尽管SLE方法能够生成空间填充和映射性能俱优的试验样本, 但同时需要耗费大量计算时间, 设计效率较低。虽然优化试验设计方法可以有效降低仿真时间和仿真次数, 但优化试验设计的全局精确寻优本身就是一个十分困难且耗时的过程, 设计效率不高。文献[8]提到在SunSPARC 20工作站寻找一个最优的25×4拉丁超立方设计(Latin hypercube design, LHD)样本需要花费几个小时, 可见确定一个最优的试验样本是十分耗时的, 这一点对于大规模试验设计尤为突出。
为了提高优化试验设计方法的效率, 同时兼顾到试验样本性能, 本文提出一种快速优化拉丁超立方试验设计方法(fast optimal Latin hypercube sampling design, FOLHD), 利用连续局部枚举方法和平移传播(translational propagation)算法[9], 快速高效生成兼具空间填充和映射性能的试验样本。通过数值试验与分析证明了该方法的有效性以及其在构造代理模型精度上的优势。
1 FOLHD方法 1.1 连续局部枚举方法快速优化拉丁超立方试验设计方法使用平移传播算法通过“平移”基础样本获得所需的试验样本。作为FOLHD方法实现基础, 基础样本必须具有优越的样本性能。本文选用连续局部枚举方法SLE生成基础样本, 该方法基于最大最小距离准则, 设计生成的样本点具有出色的空间填充性能和映射性能。
使用SLE方法在n维空间内生成m个样本点, 需先将设计空间等分成mn个设计子空间,即空间单元, 再在总共mn个空间单元(n=2时, 空间单元为正方形; n=3时, 空间单元为正方体, 以此类推)中选择其中m个空间单元放置m个样本点。每个样本点都将在mn个空间单元中逐格决定, 而每格中只能产生1个样本点。在n维空间内产生第1个样本点后, 此时格就是可能产生样本点的(m-1)n-1个空间单元。在产生第2个样本点后, 格就变成(m-2)n-1个空间单元, 以此类推(n=2时, 格为列; n=3时, 格为面)。对于n维问题, SLE方法具体实现过程如下:
1) 将设计空间均匀分成mn个空间单元, 然后逐格生成样本点。对于第1个样本点P1, 可在第1格随机产生。定义点P1位置(i1, j1, …, g1, 1)(i1, j1, …, g1∈{1, 2, …, m}), 将点P1放入样本集P={P1};
2) 对于第2个样本点P2, 将在第2格中产生。坐标为(i1, j1, …, g1, 1)位置已被P1占用, 因此样本点P2只能放置在第2格剩余空间单元中。定义点P2位置坐标为(i2, j2, …, g2, 2), 第2格剩余空间单元位置与现有样本点P1之间最大距离可表示为max(d((i2, j2, …, g2, 2), P1))(i2∈{ri|ri=1, 2, …, m; ri≠i1}, j2∈{rj|rj=1, 2, …, m; rj≠j1}, …, g2∈{rg|rg=1, 2, …, m; rg≠g1})。计算第2格剩余空间单元位置与样本点P1距离, 样本点P2将被放置在距离点P1最远的空间单元中。更新样本集P={P1, P2};
3) 对于第k个样本点Pk, {k|k=3, 4, …, m-1}, 表明已有样本点{P1, P2, …, Pk-1}已经占用了k-1个格。因此, 第k个样本点只能出现在第k格剩余空间单元中, 即Pk(ik, jk, …, gk, k)(ik∈{ri|ri=1, 2, …, m; ri≠i1, i2, …, ik-1}, jk∈{rj|rj=1, 2, …, m; rj≠j1, j2, …, jk-1}, …, gk∈{rg|rg=1, 2, …, m; rg≠g1, g2, …, gk-1})。在第k格剩余空间单元中, 分别计算各空间单元位置和现有样本点{P1, P2, …, Pk-1}之间距离, 并将最小距离值作为特征值, 得到m-k+1个特征值。最大特征值对应空间单元便是第k个样本点坐标位置(ik, jk, …, gk, k), 第k个样本点Pk与现有样本点P之间最大最小距离可表示为max(d((ik, jk, …, gk, k), P))。更新样本集P={P1, P2, …, Pk-1, Pk};
4) 重复步骤3直至完成m-1个样本点生成;
5) 第m个样本点被放置在剩余的最后1个空间单元中。
为了更加直观描述SLE方法, 采用上述方法在二维平面内生成4个样本点, 如图 1所示。按上述步骤1, 设计空间将被均分为4×4个空间单元, 点P1被随机分配在第1列第2行的空间单元(2, 1)中。步骤2中, P2将在第2列(格)剩余空间单元({1, 3, 4}, 2)中产生。计算剩余空间单元与点P1距离, 最大距离对应的空间单元(4, 2)被用来放置点P2。参照步骤3, 第3列还有空间单元(1, 3)和(3, 3)未被占用, 分别计算点(1, 3)与{P1, P2}之间距离为2.236和3.162, 所以最小距离2.236为空间单元(1, 3)的特征距离。同样地, 分别计算点(3, 3)与{P1, P2}之间距离为2.236和1.414, 最小距离1.414为空间单元(3, 3)的特征距离。第3列空间单元特征距离为{2.236, 1.414}, 其中2.236为最大特征距离, 所以空间单元(1, 3)被用来放置点P3。点P4则被放置在剩下最后1个空间单元(3, 4)中。
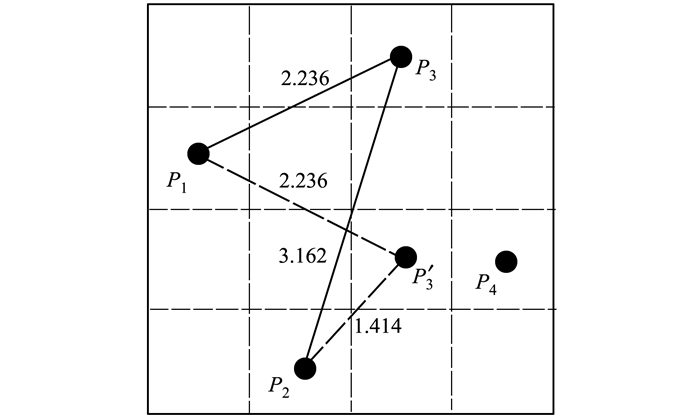
|
| 图 1 SLE方法样本点生成过程 |
图 2和图 3分别展示了SLE和LHD方法(采用MATLAB命令函数Lhsdesign获得)在三维空间内产生32个样本点分布情况, 并将样本点映射至对应二维平面内。从图中可以清楚看到, SLE和LHD方法都具有良好映射性能。但是SLE方法产生的样本点能够更均匀填充整个设计空间, 其空间填充性能优于LHD方法。
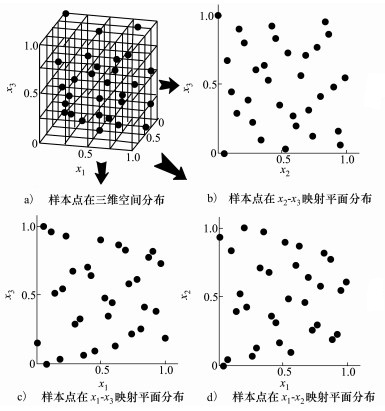
|
| 图 2 SLE方法三维空间和二维映射样本点分布 |

|
| 图 3 LHD方法三维空间和二维映射样本点分布 |
试验样本的尺寸大小(样本数量)对样本的设计时间起着重要影响, 尤其对于优化试验设计方法, 产生大尺寸试验样本所需的时间是巨大的。FOLHD方法采用平移传播算法, 通过对空间填充性能和映射性能优越的小尺寸基础样本进行“平移”来快速获得更大尺寸且性能可接受的试验样本。FOLHD方法一旦生成性能优越的基础样本, 无需进行额外的复杂优化运算, 平移传播算法计算所需时间可以忽略不计。下面将详细描述平移传播算法操作过程。
平移传播算法将设计空间每一维都一分为二, 整个设计空间被划分为等效的数量为b样本模块, 每个样本模块都将按照一定规律被基础样本填充。假设需要生成一个尺寸为mp×np试验样本, 即在np维空间中产生mp个样本点, 需要构造一个性能优越的小尺寸样本mb×nb作为基础样本。模块数量b和基础样本点数量mb计算表达式分别为

|
(1) |

|
(2) |
(1) 式和(2)式中, 基础样本维数nb与目标样本维数np保持一致, 即nb=np。
为了更加直观描述平移传播算法, 下面将通过获得一个尺寸为16×2(mp=16, np=2)样本来具体展示其运算过程。将mp=16, np=2代入(1)式和(2)式, 计算得到样本模块数量b=4, 基础样本点数量mb=4。图 4描述了平移传播算法通过“平移”基础样本得到最终试验样本的全过程。从图中可以看出, 整个设计空间被分成4个样本模块, 且每个模块都被基础样本依次填充。首先使用SLE方法在第1个样本模块中生成一个空间填充性能优越的尺寸为4×2基础样本, 如图 4a)所示。然后使用平移传播算法对基础样本进行“平移”, 依次填充剩余3个样本模块。为了保留LHD映射特性(即每个区间只有1个样本点), 在每次“平移”过程中需移动1个区间。基础样本在水平方向“平移”过程中(移动mp/2区间), 同时在竖直方向移动1个区间, 如图 4b)所示。图 4b)中2个基础样本模块在随后的“平移”过程中合为1个新样本模块, 新模块中基础样本在竖直方向移动mp/2区间, 同时在水平方向移动1个区间后, 获得最终所需试验样本, 如图 4c)所示。

|
| 图 4 平移传播算法生成试验样本过程 |
由于平移传播算法参数mb和b必须为整数, 因此FOLHD方法只能生成特定尺寸样本。为了更好地发挥FOLHD方法优势, 本文提出一种样本尺寸调整策略来解决这个问题。下一节将详细介绍样本尺寸调整策略。
1.3 样本尺寸调整策略对于特定尺寸试验样本, 通过(1)式和(2)式计算得到的参数mb可能不是整数, 即使用FOLHD方法无法直接获取所需尺寸样本。为了克服这个难题, 本文提出了样本尺寸调整策略, 该策略通过对参数mb向上取整, 生成尺寸更大的试验样本。随后计算每个样本点到设计空间中心点距离, 逐个剔除距离最大的样本点和相应区间(为了保持LHD映射特性)。最后将剩余样本点按比例填充至整个设计空间, 获得所需尺寸样本。图 5给出了尺寸为13×2样本的调整过程。
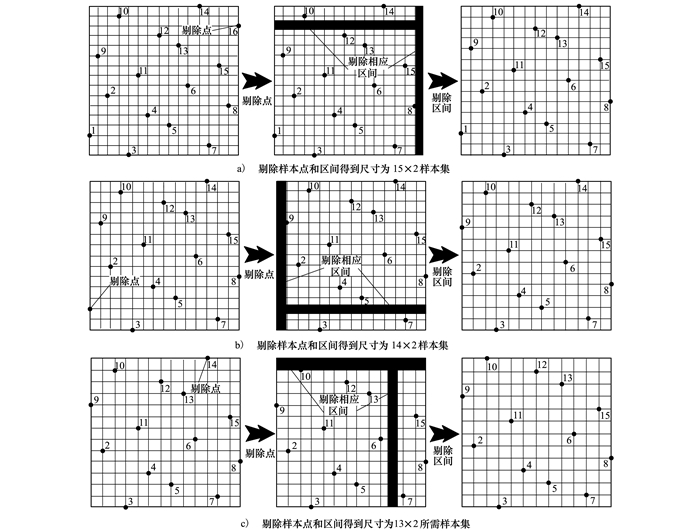
|
| 图 5 尺寸为13×2样本的调整过程 |
为了获得尺寸为13×2样本(mp=13, np=2), 需要先使用FOLHD方法生成尺寸较大的样本。通过(1)式和(2)式得到基础样本点数量mb=3.25, 向上取整得到mb=4, 进一步计算得到mp=16。采用FOLHD方法生成尺寸为16×2样本, 随后仅需对其中3个样本点进行剔除即可完成样本尺寸调整。计算所有样本点与设计空间中心点距离, 然后剔除距离设计空间中心最远的样本点, 获得尺寸为15×2样本, 如图 5a)所示。图中点16距离设计空间中心最远, 故先将其剔除。需要注意的是, 直接剔除样本点会破坏LHD映射特性, 因此在剔除样本点的同时还要剔除对应的样本区间(图中阴影部分)。在图 5b)和5c)中, 点1和点14及其对应区间先后被剔除, 最后将剩余的13个样本点按比例填充至整个设计空间, 获得所需尺寸样本。FOLHD方法能够通过样本尺寸调整策略快速获得任意尺寸样本, 同时保证生成样本的良好空间填充和映射性能。
1.4 FOLHD方法总结快速优化拉丁超立方试验设计方法兼顾了试验样本的设计效率和性能。在合理利用计算资源条件下, 尽可能寻找性能优越的试验样本, 其优势在于效率高, 计算时间短且生成的试验样本性能良好。FOLHD方法流程如图 6所示, 具体步骤总结如下:
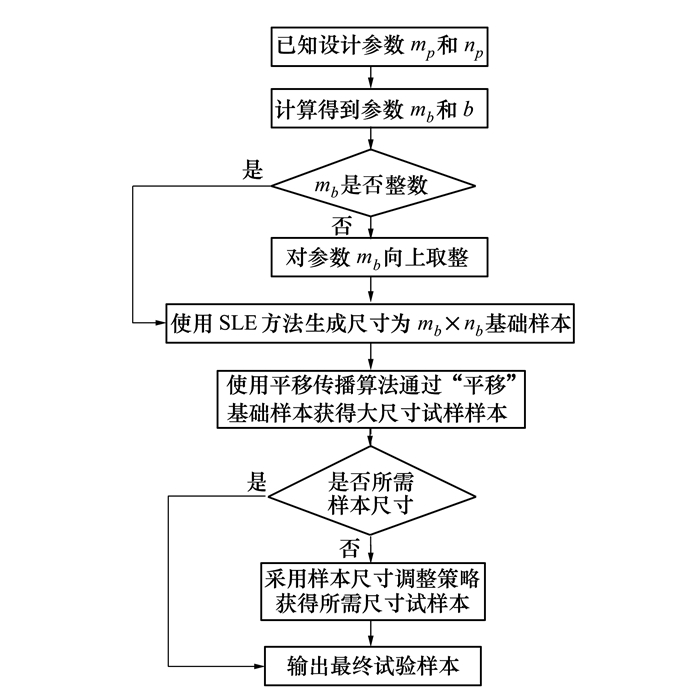
|
| 图 6 FOLHD方法流程图 |
1) 给定设计参数mp和np, 通过(1)式和(2)式计算得到基础样本点数量mb和样本模块数量b;
2) 判断mb是否为整数?如果不是, 则对参数mb向上取整;
3) 使用SLE方法生成性能优越的尺寸为mb×nb基础样本;
4) 使用平移传播算法通过“平移”基础样本获得大尺寸试验样本;
5) 判断生成的试验样本尺寸是否满足设计要求?如果不满足, 则采用样本尺寸调整策略剔除多余的样本点, 获得所需尺寸试验样本;
6) 结束程序, 输出最终试验样本。
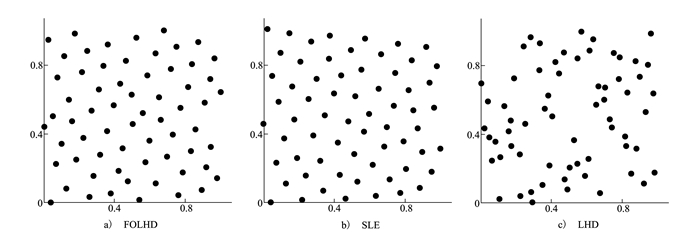
采用FOLHD、SLE和LHD 3种方法均生成尺寸为64×2试验样本, 空间分布情况如图 7所示。比较图 7a)和7b)可以发现, FOLHD方法空间填充性能与SLE方法表现相当, 但FOLHD方法设计效率却远高于SLE。同样和图 7c)中LHD方法相比, FOLHD方法产生的样本点能够更加均匀地分布至整个设计空间, 其空间填充性能远优于LHD方法。
|
| 图 7 FOLHD、SLE和LHD方法试验样本性能比较 |
优化试验设计方法将某种优化准则作为目标函数, 使用优化算法如遗传算法、模拟退火算法等进行优化计算来获得试验样本, 这将耗费大量计算时间和计算资源, 尤其对于大尺寸试验样本。本文提出的快速优化拉丁超立方试验设计方法FOLHD使用连续局部枚举方法和平移传播算法, 将大尺寸试验样本的优化问题转换为小尺寸基础样本寻优, 设计效率高于传统优化试验设计方法。下面将通过对不同规模的样本进行性能和效率测试, 并与SLE和LHD试验设计方法进行比较。
2.1 样本性能测试为了定量描述FOLHD方法的空间填充性能, 本文采用3种评价准则:最大最小距离dmin, ϕp和最小势能U对不同规模样本进行测试, 并与SLE和LHD方法进行比较。其中, dmin值越大, ϕp和U值越小, 表示试验样本空间填充性能越好。3种评价准则的具体介绍如下。
1) 最大最小距离dmin准则。最大最小距离准则首先由Johnson等提出, 目标是最大化试验样本点之间最小距离dmin, 即满足如下要求
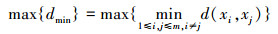
|
(3) |
式中, m为样本点数量, d(xi, xj)表示任意2个样本点xi和xj之间距离

|
(4) |
式中, n为设计变量数。本文如无说明, 则取t=2。
2) ϕp准则。Morris和Mitchell于1995年对最大最小距离准则进行扩展应用, 提出ϕp准则。若一个试验设计被称为ϕp最优设计, 则它满足以下条件
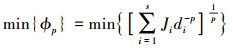
|
(5) |
对于给定的试验设计方案, 计算任意2个样本点间距离dij (此处t=1), 将这些距离进行排序, 得到距离函数取值列表(d1, d2, …, ds)和对应的索引列表(J1, J2, …, Js)。di表示不同距离值, 且d1 < d2 < … < ds, Ji是距离为di点对的数量, s为不同距离值数目。式中p为正整数, 设为50。
3) 最小势能U准则。最小势能U准则由Jourdan等提出, 该准则受物理规律启发:当系统势能达到最小时, 会处于平衡状态。势能U表达式为
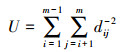
|
(6) |
采用FOLHD、LHD和SLE 3种方法分别生成同一规模试验样本,同时为了减小试验随机误差,使用FOLHD和LHD重复生成样本500次,SLE为100次,随后对获得的试验样本进行归一化。采用dmin, ϕp和U对试验样本进行评价,并分别记录函数值dmin, ϕp和U最优值、最差值以及平均值。表 1和2分别给出了二维和三维情况下3种试验设计方法生成不同规模试验样本的测试结果,表中的最优平均值使用粗体表示。
| n=2 | FOLHD | LHD | SLE | ||||||||||
| m | 准则 | 最优值 | 最差值 | 平均值 | 最优值 | 最差值 | 平均值 | 最优值 | 最差值 | 平均值 | |||
| 16 | dmin | 0.189 | 0.149 | 0.156 | 0.193 | 0.065 | 0.111 | 0.211 | 0.149 | 0.200 | |||
| ϕp | 5.453 | 6.802 | 6.559 | 5.245 | 15.437 | 9.240 | 4.744 | 6.708 | 5.090 | ||||
| U | 650.2 | 705.5 | 659.3 | 702.7 | 1503.3 | 966.6 | 622.4 | 663.2 | 638.0 | ||||
| 32 | dmin | 0.116 | 0.072 | 0.093 | 0.088 | 0.032 | 0.057 | 0.161 | 0.091 | 0.134 | |||
| ϕp | 8.718 | 14.06 | 11.54 | 11.41 | 31.73 | 18.12 | 6.479 | 10.96 | 7.635 | ||||
| U | 3 682.6 | 4 041.3 | 3 863.0 | 4 482.4 | 8 516.5 | 5 594.6 | 3 585.0 | 3 722.8 | 3 629.8 | ||||
| 64 | dmin | 0.085 | 0.035 | 0.059 | 0.045 | 0.017 | 0.028 | 0.106 | 0.035 | 0.093 | |||
| ϕp | 11.86 | 28.57 | 18.75 | 22.25 | 58.06 | 36.38 | 9.501 | 28.17 | 11.22 | ||||
| U | 18 750 | 20 602 | 19 408 | 24 282 | 41 036 | 30 131 | 18 540 | 19 374 | 18 716 | ||||
| 128 | dmin | 0.053 | 0.018 | 0.034 | 0.023 | 0.007 | 0.014 | 0.078 | 0.025 | 0.065 | |||
| ϕp | 19.20 | 57.59 | 34.36 | 44.22 | 134.5 | 73.40 | 13.30 | 40.16 | 16.29 | ||||
| U | 92 929 | 99 400 | 95 453 | 126 197 | 196 399 | 152 847 | 91 502 | 93 624 | 91 996 | ||||
| n=3 | FOLHD | LHD | SLE | ||||||||||
| m | 准则 | 最优值 | 最差值 | 平均值 | 最优值 | 最差值 | 平均值 | 最优值 | 最差值 | 平均值 | |||
| 16 | dmin | 0.327 | 0.275 | 0.301 | 0.312 | 0.139 | 0.211 | 0.327 | 0.163 | 0.270 | |||
| ϕp | 3.149 | 3.689 | 3.378 | 3.204 | 7.217 | 4.856 | 3.068 | 6.124 | 3.835 | ||||
| U | 298.3 | 336.6 | 312.6 | 335.2 | 516.0 | 409.0 | 313.4 | 359.1 | 329.9 | ||||
| 32 | dmin | 0.262 | 0.133 | 0.222 | 0.185 | 0.074 | 0.126 | 0.279 | 0.079 | 0.197 | |||
| ϕp | 3.927 | 7.624 | 4.744 | 5.472 | 13.47 | 8.139 | 3.615 | 12.66 | 5.313 | ||||
| U | 1 538.8 | 1 646.1 | 1 578.6 | 1 739.0 | 2 604.4 | 2 028.4 | 1 570.0 | 1 761.2 | 1 626.3 | ||||
| 64 | dmin | 0.149 | 0.065 | 0.111 | 0.115 | 0.046 | 0.076 | 0.206 | 0.027 | 0.139 | |||
| ϕp | 6.905 | 15.49 | 9.59 | 8.914 | 21.54 | 13.60 | 4.986 | 36.37 | 8.478 | ||||
| U | 7 449.3 | 8 524.2 | 7 897.0 | 8 409.2 | 10 853 | 9 280.8 | 7 402.2 | 8 732.2 | 7 533.5 | ||||
| 128 | dmin | 0.074 | 0.039 | 0.056 | 0.068 | 0.028 | 0.045 | 0.164 | 0.014 | 0.099 | |||
| ϕp | 13.92 | 26.65 | 19.00 | 14.94 | 35.17 | 22.74 | 6.206 | 73.32 | 12.78 | ||||
| U | 33 509 | 37 468 | 35 244 | 37 271 | 44 260 | 40 370 | 32 795 | 38 283 | 33 219 | ||||
分析表 1结果可知,FOLHD方法生成的试验样本的性能评价准则ϕp和U平均值都小于LHD方法,而dmin平均值都大于LHD方法。由此表明FOLHD方法生成的试验样本性能优于LHD方法。值得说明的是,FOLHD方法生成的试验样本性能表征参数在最差的情况下仍比LHD方法平均情况要好。另外,从表中测试结果来看,SLE方法在样本性能方面表现最优。事实上,SLE方法获得的试验样本性能最优与事先预测是一致的。然而SLE方法无法兼顾样本性能与设计效率,需要耗费大量计算时间。同样分析表 2测试结果,得到的结论与表 1基本一致。需要特别指出的是,在三维情况下,FOLHD方法生成的样本性能与SLE方法基本一致,尤其在样本尺寸为16×3和32×3上,FOLHD方法表现甚至优于SLE。综上所述,本文提出的FOLHD方法具有良好的样本性能,非常接近SLE方法,少数情况甚至还优于SLE。另外,LHD方法因其简单高效被科研人员广泛使用,而FOLHD方法能够在极短时间内设计生成空间填充性能远优于LHD方法的试验样本。
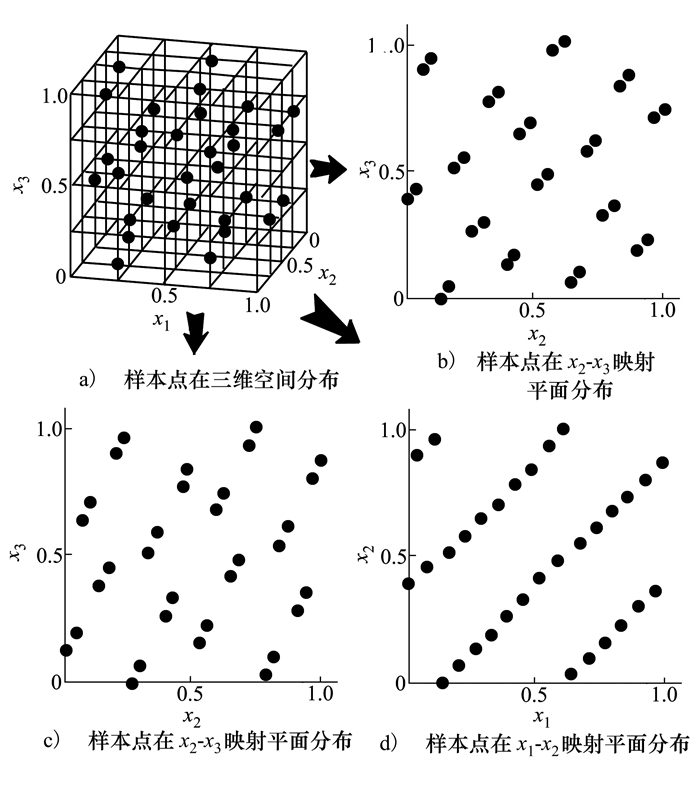
为了进一步反映FOLHD方法样本性能,使用FOLHD和LHD方法在设计变量较多情况下生成不同规模试验样本,并同样使用dmin, ϕp和U评价准则对其进行测试,测试结果平均值见表 3。与低维情况类似,FOLHD方法样本性能总体优于LHD方法。针对不同规模样本,FOLHD方法在性能参数dmin和ϕp方面表现均好于LHD方法。而对于评价准则U,FOLHD方法则没有表现出绝对优越性,在部分情况下最小势能U平均值大于LHD方法,这说明不同评价准则具有不同测试目标,可能会产生不同评价结果。本文采用多种评价准则对不同规模试验样本进行测试,克服了上述问题。图 8展示了FOLHD方法生成的尺寸为32×3样本在三维空间和二维映射平面内分布。与图 2和3相比,可以直观发现FOLHD方法在三维情况下样本分布非常均匀,空间填充性能优于LHD方法,与SLE方法相近。
| 准则 | 方法 | 样本尺寸m×n | ||||||||
| 32×4 | 64×4 | 128×4 | 64×6 | 128×6 | 256×6 | 256×8 | 512×8 | 1 024×10 | ||
| dmin | FOLHD | 0.323 | 0.252 | 0.137 | 0.440 | 0.294 | 0.316 | 0.470 | 0.322 | 0.500 |
| LHD | 0.204 | 0.139 | 0.094 | 0.275 | 0.211 | 0.163 | 0.274 | 0.226 | 0.282 | |
| ϕp | FOLHD | 3.204 | 4.163 | 7.905 | 2.403 | 3.846 | 3.367 | 2.325 | 3.396 | 2.347 |
| LHD | 4.994 | 7.353 | 10.809 | 3.679 | 4.805 | 6.214 | 3.688 | 4.480 | 3.579 | |
| U | FOLHD | 928 | 4 339 | 19 754 | 2 955 | 9 079 | 40 142 | 34 873 | 101 713 | 426 506 |
| LHD | 1 178 | 5 138 | 21 550 | 2 700 | 11 108 | 45 056 | 30 468 | 122 528 | 372 172 | |
|
| 图 8 FOLHD方法三维空间和二维映射样本点分布 |
本节对3种试验设计方法FOLHD、LHD和SLE的设计效率进行测试研究。当n≥4时,SLE方法试验20次,其他工况均测试100次,平均计算时间如表 4所示。表中计算时间是在配置为英特尔酷睿3.3 GHz处理器计算机上,并在高性能模式下测试所得。通过对比3种试验设计方法所消耗的时间可知,FOLHD和LHD方法都能快速设计生成试验样本,所需时间几乎可以忽略不计。然而,SLE方法是一种基于优化准则试验设计方法,寻优时间随样本规模增加而急剧增大,不适用于处理设计变量较多、试验成本较高的工程问题。SLE方法在生成规模为128×4样本时已经耗时长达456.54 s,当设计变量继续增加时,其所需计算时间是工程设计无法承受的,因此本节未对维数n≥6样本进行测试。
| s | ||||||||||
| 方法 | 时间 | |||||||||
| 32×2 | 64×2 | 64×3 | 128×3 | 64×4 | 128×4 | 128×6 | 256×6 | 512×8 | 1 024×10 | |
| FOLHD | 0.003 5 | 0.009 0 | 0.002 8 | 0.007 4 | 0.002 2 | 0.004 1 | 0.002 4 | 0.004 4 | 0.006 6 | 0.011 6 |
| LHD | 0.001 0 | 0.001 1 | 0.001 2 | 0.001 7 | 0.001 3 | 0.001 8 | 0.003 8 | 0.004 1 | 0.013 7 | 0.054 0 |
| SLE | 0.015 7 | 0.059 7 | 0.175 9 | 3.662 5 | 11.469 | 456.54 | ||||
FOLHD和LHD方法均能快速高效产生试验样本, 设计效率远高于SLE方法, 尤其在维度较高情况下。另外, FOLHD方法生成的试验样本空间填充性能优于LHD方法。综上所述, FOLHD方法能够很好地兼顾样本性能和设计效率, 可以快速高效地生成空间填充性能良好试验样本, 这是SLE和LHD方法所不具备的。
2.3 数值试验随着工程设计优化问题日趋复杂, 利用代理模型替代复杂耗时仿真分析模型被认为是解决问题的最有效途径之一。而试验样本优劣将直接决定所构造的代理模型精度, 不精确的代理模型精度会降低优化精度和优化效率。为了验证快速优化拉丁超立方试验设计方法FOLHD在工程设计优化应用中有效性和可行性, 选取5个经典测试函数用于构造代理模型, 同时和SLE、LHD 2种方法进行比较。本节选用径向基函数作为代理模型构造方法, 基函数采用MULTI-QUADRIC。
1) Peaks函数(PK), n=2
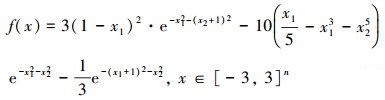
|
(7) |
2) Rastrigin函数(RS), n=2
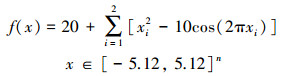
|
(8) |
3) Hartman 4-Dimensional函数(HN4), n=4

|

|
(9) |
4) Michalewicz函数(MC), n=5, 6

|
(10) |
采用3种试验设计方法FOLHD、LHD和SLE分别产生相同数量的训练样本点用来构造径向基函数模型, 训练样本点数量见表 5。另外, 在设计空间内随机选取1 024个测试点, 分别使用相对均方根误差(relative root mean square error, RRMSE)和相对最大绝对值误差(relative maximum absolute error, RMAE)评价代理模型全局精度和局部精度。RRMSE和RMAE数学表达式如下
| 函数 | 设计变量数 | 训练样本点数量 | RRMSE | RMAE | |||||
| FOLHD | LHD | SLE | FOLHD | LHD | SLE | ||||
| PK | 2 | 64 | 0.138 | 0.234 | 0.132 | 0.652 | 1.292 | 0.797 | |
| RS | 2 | 64 | 0.980 | 1.659 | 0.988 | 3.109 | 7.269 | 3.114 | |
| HN4 | 4 | 64 | 0.980 | 1.066 | 0.790 | 6.297 | 6.905 | 4.892 | |
| MC5 | 5 | 64 | 1.254 | 1.500 | 1.560 | 4.734 | 5.536 | 6.228 | |
| MC6 | 6 | 128 | 1.243 | 1.411 | 4.641 | 5.167 | |||
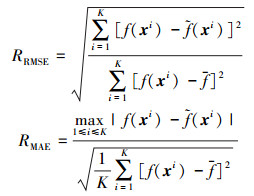
|
(11) |
式中, K为测试点数量, f(xi)和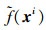
为了减小随机误差, MC5函数重复运算10次, 其他测试函数反复试验100次, 测试结果平均值如表 5所示。需要特别说明的是, 当设计变量数大于5时, SLE方法计算时间过于庞大, 因此表中并未给出函数MC6相应的测试结果。分析表中结果可知, 利用FOLHD和SLE方法生成的训练样本构建的代理模型更接近真实模型。然而, 使用SLE方法完成数值试验所需时间远高于FOLHD方法。
综合考虑代理模型精度和计算效率, 本文提出的快速优化拉丁超立方试验设计方法FOLHD更加适合设计变量较多、试验成本较高的工程优化问题。
3 结论本文针对复杂工程设计优化中, 传统优化试验设计方法需要耗费大量计算时间和计算资源的问题, 提出一种快速优化拉丁超立方试验设计方法。获得结论如下:
1) 连续局部枚举方法SLE尽管能够生成空间填充性能优越的基础样本, 但设计效率偏低, 尤其对于大尺寸试验样本。
2) 平移传播算法通过平移基础样本能够快速获得空间填充性能良好的大尺寸试验样本, 计算时间可以忽略不计。
3) 样本尺寸调整策略能够保证快速优化拉丁超立方试验设计方法快速生成任意尺寸样本, 克服了平移传播算法只能产生特定尺寸样本的缺点。
4) 试验结果表明快速优化拉丁超立方试验设计方法能够合理平衡样本性能和计算效率, 很好地弥补优化试验设计方法存在的不足, 为构造高精度代理模型提供一种有效选择, 具有一定工程意义。
| [1] | YE Pengcheng, PAN Guang, DONG Zuomin. Ensemble of Surrogate Based Global Optimization Methods Using Hierarchical Design Space Reduction[J]. Structural and Multidisciplinary Optimization, 2018, 58(2): 537-554. DOI:10.1007/s00158-018-1906-6 |
| [2] | LIU Haitao, ONG Yewsoon, CAI Jianfei. A Survey of Adaptive Sampling for Global Metamodeling in Support of Simulation-Based Complex Engineering Design[J]. Structural and Multidisciplinary Optimization, 2017, 57(1): 393-416. |
| [3] | LIU Haitao, XU Shengli, WANG Xiaofang. Sequential Sampling Designs Based on Space Reduction[J]. Engineering Optimization, 2015, 47(7): 867-884. DOI:10.1080/0305215X.2014.928816 |
| [4] | DONG Huachao, SONG Baowei, DONG Zuomin, et al. Multi-Start Space Reduction(MSSR) Surrogate-Based Global Optimization Method[J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 907-926. DOI:10.1007/s00158-016-1450-1 |
| [5] |
刘新亮, 郭波. 基于改进ESE算法的多目标优化试验设计方法[J]. 系统工程与电子技术, 2010, 32(2): 410-414.
LIU Xinliang, GUO Bo. Multi-Objective Experimentation Design Optimization Based on Modified ESE Algorithms[J]. Systems Engineering and Electronics, 2010, 32(2): 410-414. (in Chinese) |
| [6] |
刘晓路, 陈英武, 荆显荣, 等. 优化拉丁方试验设计方法及其应用[J]. 国防科技大学学报, 2011, 33(5): 73-77.
LIU Xiaolu, CHEN Yingwu, JING Xianrong, et al. Optimized Latin Hypercube Sampling Method and Its Application[J]. Journal of National University of Defense Technology, 2011, 33(5): 73-77. (in Chinese) DOI:10.3969/j.issn.1001-2486.2011.05.015 |
| [7] | ZHU Huaguang, LIU Li, LONG Teng, et al. A Novel Algorithm of Maximin Latin Hypercube Design Using Successive Local Enumeration[J]. Engineering Optimization, 2012, 44(5): 551-564. DOI:10.1080/0305215X.2011.591790 |
| [8] | YE Kenny, LI William, SUDJIANTO Agus. Algorithmic Construction of Optimal Symmetric Latin Hypercube Designs[J]. Journal of Statistical Planning and Inference, 2000, 90(1): 145-159. DOI:10.1016/S0378-3758(00)00105-1 |
| [9] | VIANA Felipe, Venter Gerhard, BALABANOV Vladimir. An Algorithm for Fast Optimal Latin Hypercube Design of Experiments[J]. International Journal for Numerical Methods in Engineering, 2010, 82(2): 135-156. |
2. Key Laboratory for Unmanned Underwater Vehicle, Northwestern Polytechnical University, Xi'an 710072, China


