结构优化设计问题可转化成含有设计变量、目标函数和约束条件的数学规划问题,该数学规划问题的求解就是在满足约束条件限制下求得使目标函数值取极值的设计变量。在实际工程结构优化设计中,由于问题的复杂性与不确定性,往往很难建立目标函数和约束条件函数关于设计变量的显式表达式,数值计算方法常常需要大量调用有限元计算,才能获得一个合理的优化结果,计算效率不高。而使用结构近似重分析方法,构建结构近似模型(代理模型),可以避免大量反复的调用有限元计算,提高计算效率[1]。目前应用于结构优化设计的代理模型主要有响应面法、Kriging模型、径向基函数方法、神经网络法和支持向量机法等。其中支持向量机是基于统计学习理论的一种机器学习方法,与传统的代理模型方法相比,其突出的优点是具有较强的小样本学习能力和泛化能力[2]。最小二乘支持向量机(least squares support vector, LSSVM)[3]是对支持向量机(squares support vector, SVM)的一种改进算法,利用等式约束代替不等式约束,将二次规划问题转化为线性方程组的问题,其缩短了训练时间,计算量较小,训练结果更为精确,适合工程应用,在结构优化领域已经实现了应用。
交叉熵方法(cross entropy, CE)最初由Rubinstein于1997年提出,用于稀疏事件模拟[4],1999年拓展为随机优化方法并应用于旅行商问题[5]。2005年Chepuri等人[6]采用交叉熵方法处理车辆路径优化问题并取得了令人满意的结果。2009年,Santosa[7]应用交叉熵方法对支持向量机进行参数寻优。2015年,Ghidey[8]对交叉熵方法在可靠性优化设计(reliability based design optimization, RBDO)问题中的精度和效率进行了详细的讨论研究。2017年任超等[9]对交叉熵方法进行了改进,证明了改进交叉熵方法在随机优化方法上的效率与精度。交叉熵方法作为一种类蒙特卡罗方法在旅行商、路径优化,参数寻优等众多优化实例中都表现出了优异的寻优能力。但其蒙特卡罗特性在求解隐式结构优化问题时仍需调用大量有限元计算,阻碍了其在结构优化领域中的应用。目前国内外对交叉熵在结构优化领域的研究少见于公开发表文献。
本文着眼于交叉熵方法在结构优化中的应用,采用最小二乘支持向量机与改进交叉熵方法相结合得到组合优化方法(ICE-SVM)。基于最小二乘支持向量机建立代理模型,模拟结构输入与输出响应之间的关系。代替耗时较长的有限元分析,避免交叉熵方法调用大量有限元计算。为验证该方法的有效性。分别采用最小二乘支持向量机与改进交叉熵方法相结合的组合优化方法(ICE-SVM)与传统交叉熵方法与最小二乘支持向量机的组合优化方法(CE-SVM)对数值算例与工程算例的优化问题进行求解。
1 最小二乘支持向量机LSSVM可用于分类与回归问题,本文主要利用LSSVM进行回归估计,其算法如下:
给定训练样本集
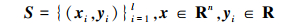
|
(1) |
式中, d为输入参数维数, xi为输入向量, yi为输出响应, l为训练样本数量。
LSSVM的回归函数可由(2)式表示
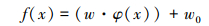
|
(2) |
根据二次损失函数作为结构风险最小化原则, 对(2)式的求解转化为优化问题:
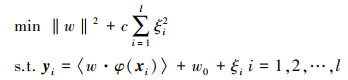
|
(3) |
式中,w和w0为算法控制参数, ξ为松弛变量, c为正则化参数, φ(·)为映射函数。引入Lagrange函数
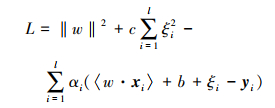
|
(4) |
式中,αi为Lagrange乘子。根据最优化条件, 将(4)式分别对w, w0, ξi和αi求偏导, 置零后转化为矩阵形式, 即
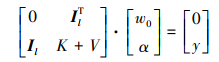
|
(5) |
式中,y=[y1, y2, …, yl]T; Il=[1, 1, …, 1]T∈Rl; α=[α1, α2, …, αl]T; K={ki, j|i, j=1, 2, …, l}; V=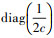
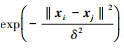
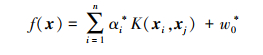
|
(6) |
交叉熵是对2个概率分布差异性的一种度量, 也可称为KL散度(Kullback-Leibler divergence)。设fX(x)和hX(x)是给定的2个概率密度函数, x为n维随机输入变量, 则fX(x)和hX(x)的交叉熵可定义为:
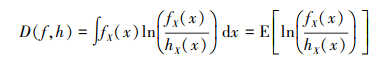
|
(7) |
式中, D(·, ·)为交叉熵, 显然, 当fX(x)=hX(x)时, D(f, h)=0;当fX(x)≠hX(x), D(f, h)>0。
对于优化问题, 可以将优化问题与概率估计相关联。考虑求函数s(x)的极小值问题
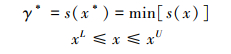
|
(8) |
在γ上定义一组概率密度函数[fX(x; v)]和指示函数
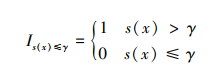
|
(9) |
人工构建一个可靠性问题, 即
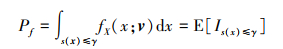
|
(10) |
式中, Pf为可靠性问题的失效概率, v为参数向量, γ为函数s(x)的一个阀值。当γ=γ*时, (10)式为一个特殊的可靠性问题, 此时Pf=0。因此, 可以利用(10)式将优化问题转化为可靠性问题。
采用交叉熵方法求解优化问题时, 通过迭代更新概率密度函数fX(x; v)中的参数向量v来驱动概率密度函数f和阀值γ进行更新。在迭代过程中, 将得到一系列的概率密度函数fX(x; v1), fX(x; v2), …, 并收敛至一个最优概率密度函数f*, 其对应的函数值即可认为是最优值x*。因当阀值γ接近或者等于最优值x*时, 此时从概率密度函数fX(x; vk)抽样将会以大概率得到一个非常接近或者等于最优值x*的点, 从而达到优化的目的。
传统交叉熵方法步骤如下:
1) 初始化待定分布参数fX(x; v0), 随机样本数N, 问题维数n, 迭代次数记为k=0
2) 从fX(x; vk)产生N个随机样本{x1, x2, …, xN}, 计算目标函数值{s(xi)}, 按照优劣排序并取其靠前的“精英样本”ρ0N。设bk为目标函数值的阀值, 即有bk=s[ρ0N], 其中ρ为分位数值。通过“精英样本”{x1, x2, …, x[ρ0N]}来估计新的分布参数值vk+1
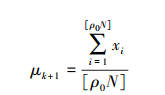
|
(11) |
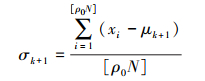
|
(12) |
3)为使重要密度参数vk+1的更新更平滑, 在交叉熵优化算法中引入一个平滑参数α, 并按(13)式更新分布参数
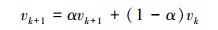
|
(13) |
4) 若max(σk+1)<εvk+1(ε为预设的精度值), 返回μk+1作为优化问题的最优解, 算法停止, 此时的μk+1是一个n维向量, 即优化后的设计变量; 否则, 设k=k+1, 转到步骤2)。
2.2 基于改进交叉熵支持向量机的结构优化任超等[9]对传统交叉熵方法在处理优化问题时的优缺点进行了讨论, 在参数更新策略、平滑参数调整和变异操作等3个方面对传统交叉熵算法进行改进, 具体改进叙述详见文献[9]。本文在其基础上将改进交叉熵方法与支持向量机相结合并应用于结构优化领域。
改进交叉熵方法其参数更新策略为:
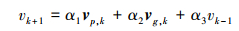
|
(14) |
式中,vp, k={μp, k, σp, k2}, 为“局部最优样本”的分布参数; vg, k={μg, k, σg, k2}为“全局最优样本”的分布参数。α1, α2和α3为新的平滑参数, 且α1+α2+α3=1。
平滑参数自适应调整公式为:
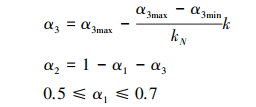
|
(15) |
式中,kN为迭代次数总数, k为迭代次数, α1为光滑参数1, α2为光滑参数2, α3为光滑参数3。
为避免陷入局部最优, 增加了扰动, 扰动函数为:
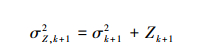
|
(16) |
式中,σk+12为未施加扰动的第k+1次迭代中的样本方差, σZ, k+12为施加扰动后的样本方差, Zk+1为扰动函数。
文献[13]比较了几种不同的抽样方式, 如简单随机抽样(simple random sampling, SRS)、拉丁超立方抽样(latin hypercube sampling, LHS)、CVT抽样(centroidal voronoi tessellation, CVT)和LCVT抽样(‘Latinized’ CVT), 结果表明LCVT抽样方法性能最好。因此本文采用LCVT抽样。同时采用交叉验证方法(K-fold cross validation)得到支持向量机控制参数。
为避免不同量纲的输入变量对SVM训练结果的影响, 在利用支持向量机模型进行预测时, 需对训练样本进行归一化, 预测结果进行反归一化, 反归一化与归一化互逆。归一化公式如下:
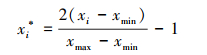
|
(17) |
式中,xi为归一化前的数据, xi*为归一化后的数据, xmax和xmin为归一化前数据的最大值和最小值。
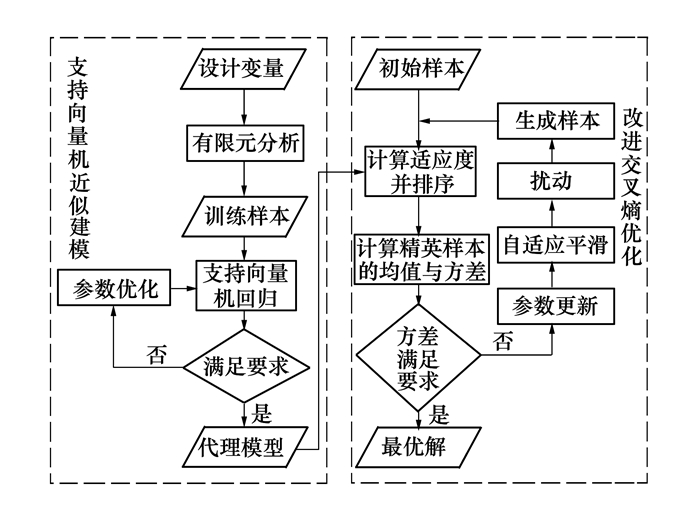
支持向量机与改进交叉熵的优化流程见图 1:
|
| 图 1 改进交叉熵支持向量机流程图 |
大致可分为以下几步:
1) 利用有限元分析方法获得训练样本;
2) 基于支持向量机训练与建立代理模型;
3) 代理模型替代有限元分析, 改进交叉熵方法搜索寻优;
4) 检查最优解的误差。
3 算例 3.1 算例1Brain函数作为一个经典的代理模型测试函数, 常用来测试代理模型的精度, 其具有3个全局最优点, 其表达式如下:
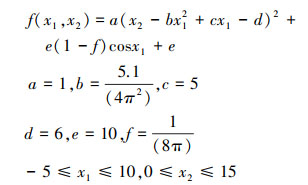
|
(18) |
训练样本分别用LHS、CVT、LCVT抽样方法获得, 测试样本用SRS获得, 计算训练样本及测试样本的均方误差和相关系数, 同时参考文献[14]的做法, 用等高线图及均方误差与回归系数来衡量代理模型质量。
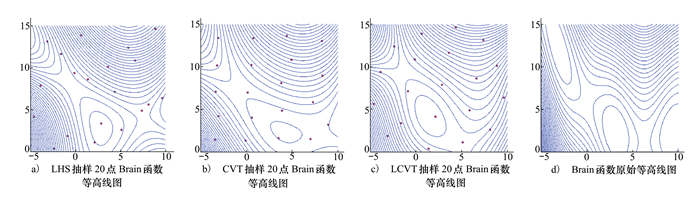
如图 2所示, CVT抽样与LCVT抽样在设计空间上分布更均匀, LCVT抽样在模型近似重构上较LHS和CVT抽样质量更好。
|
| 图 2 3种不同抽样方法与函数原始等高线图 |
表 1给出了不同抽样方式对代理模型质量的影响。R2为回归相关系数, MSE为均方误差(mean square error, MSE), 从表 1可以得出LCVT抽样在泛化性与推广性上较LHS与CVT抽样更好。
| 抽样方式 | MSE(train) 20 |
R2(train) 20 |
MSE(test) 10 000 |
R2(test) 10 000 |
| LHS | 12.133 8 | 0.995 4 | 170.693 6 | 0.934 4 |
| CVT | 14.412 5 | 0.993 4 | 152.743 1 | 0.941 3 |
| LCVT | 20.689 2 | 0.991 9 | 87.114 9 | 0.966 5 |
该算例来自文献[15], 求解(19)式和(20)式所示的最小化问题:
Minimize:
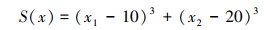
|
(19) |
Subject to:
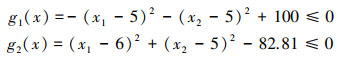
|
(20) |
式中,13≤x1≤100, 0≤x2≤100。文献中给出的最优解参考值x*={14.095 0, 0.843 0}T, 最优值参考值为S(x)=-6 961.813 9。
为验证本文提出的ICE-SVM方法的优点, 采用单步法[16]构建CE-SVM与ICE-SVM, 即进行一次试验设计和抽样, 获取所需样本点并以此构造近似代理模型。在单步法中样本数量对代理模型精度有显著影响, 故分别采用100, 300, 500, 1 000个样本点进行近似建模。为避免一次计算结果的偶然性, 分别对2种算法进行100次计算, 并得到其统计学性能。CE-SVM算法参数设置如下:单层样本量N=2 000, 迭代次数it_ max=250, 分位数ρ=0.01, 平滑参数α=0.9, 分布参数初值为μ0={56.5, 50}T和σ0={20, 20}T。ICE-SVM算法的参数设置如下:平滑参数3中α3min=0.1, α3max=0.3, 平滑参数1为α1=0.6(1-α3), 平滑参数2为α2=0.4(1-α3), 扰动系数Zk=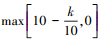
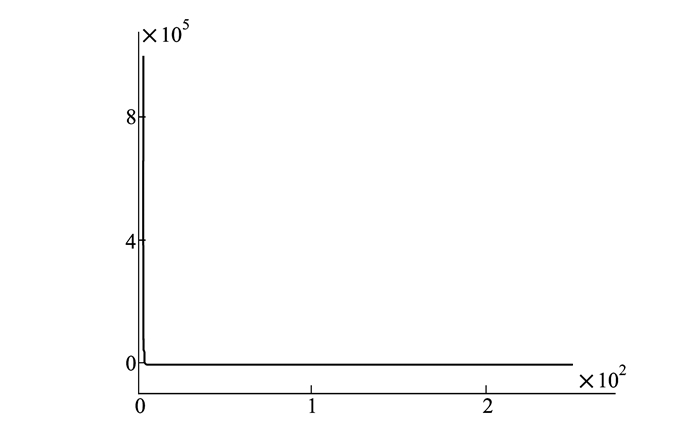
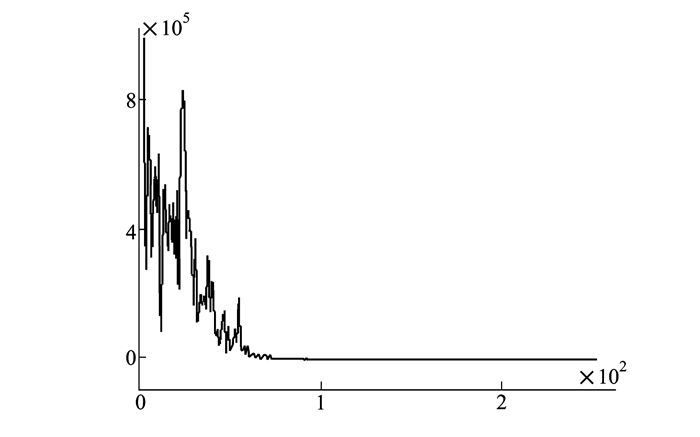
如图 3和图 4所示, CE-SVM的迭代速度非常快, 在不到20次的迭代中就找到了“最优解, ”ICE-SVM方法虽然迭代速度不及CE-SVM, 但同样在不超过100次的迭代中找到了“最优解”。
|
| 图 3 CE-SVM方法目标函数值变化趋势 |
|
| 图 4 ICE-SVM方法目标函数值变化趋势 |
表 2给出了2种优化方法的优化结果, 表 2中, S′(x)和g′(x)分别表示代理模型目标函数值与约束值, δ表示为S′(x)与理论值S(x)的相对误差, 如表 2所示, ICE-SVM的计算精度明显比CE-SVM好, 同时随着样本数量的增加, ICE-LSSVM与CE-SVM的计算结果逐步接近于目标函数理论解, 在样本数量为1 000时, CE-SVM的计算结果与理论值的相对误差为15.643 3%, 而ICE-LSSVM的计算结果与理论值的相对误差仅为0.551%, 小于1%, 表现出优异的计算能力, 其计算结果可以认为满足设计要求。表 3给出了2种算法独立运行100次的计算结果。表中:SD表示标准差, COV表示变异系数。如表 3所示, ICE-SVM的SD值与COV值均比训练样本相同的CE-SVM小, 可以认为其计算结果是可靠的, COV值较小同时也表明ICE-SVM在鲁棒性与结果稳定性上比CE-SVM更好, 综上, ICE-SVM虽然在速度上不及CE-SVM, 但是计算精度、鲁棒性与结果稳定性上较CE-SVM好。
| 方法 | LCVT抽样 | x1 | x2 | S′(x) | g′1(x) | g′2(x) | δ/% |
| CE-SVM | 100 | 14.995 2 | 5.335 5 | -2.908 4×103 | 0.001 76 | 0.003 0 | 58.222 |
| ICE-SVM | 100 | 14.954 9 | 5.309 2 | -2.923 4×103 | 1.352 0×10-4 | 1.531 9×10-4 | 58.006 |
| CE-SVM | 300 | 14.661 4 | 2.435 5 | -5.298 3×103 | -0.233 9 | -1.210 9 | 23.894 |
| ICE-SVM | 300 | 13.702 6 | 0.154 7 | -7.688 3×103 | -0.001 1 | -0.001 2 | 10.435 |
| CE-SVM | 500 | 14.547 0 | 2.034 6 | -5.643 7×103 | 7.076 5×10-4 | -0.869 4 | 18.934 |
| ICE-SVM | 500 | 14.115 9 | 0.906 3 | -6.756 5×103 | 3.661 7×10-4 | 4.128 0×10-4 | 2.949 |
| CE-SVM | 1 000 | 14.508 4 | 1.871 2 | -5.872 8×103 | -0.144 3 | 0.627 4 | 15.643 |
| ICE-SVM | 1 000 | 14.114 1 | 0.880 9 | -6.923 4×103 | -0.002 5 | -0.001 7 | 0.551 |
| 方法 | LCVT抽样 | 最优设计 | 平均设计 | 最差设计 | SD | COV |
| CE-SVM | 100 | -2.922 5×103 | -2.825 6×103 | -2.541 1×103 | 71.501 9 | 0.025 3 |
| ICE-SVM | 100 | -2.923 5×103 | -2.923 5×103 | -2.923 8×103 | 0.003 5 | 1.191 7×10-6 |
| CE-SVM | 300 | -6.429 5×103 | -5.574 2×103 | -4.199 3×103 | 402.863 6 | 0.072 3 |
| ICE-SVM | 300 | -7.689 6×103 | -7.648 8×103 | -7.346 9×103 | 56.568 3 | 0.007 4 |
| CE-SVM | 500 | -6.009 8×103 | -5.271 4×103 | -4.069 1×103 | 316.314 9 | 0.060 0 |
| ICE-SVM | 500 | -6.757 2×103 | -6.743 3×103 | -6.612 8×103 | 21.277 9 | 0.003 2 |
| CE-SVM | 1000 | -6.025 0×103 | -5.332 7×103 | -4.112 5×103 | 329.592 9 | 0.061 8 |
| ICE-SVM | 1000 | -6.928 5×103 | -6.904 3×103 | -6.468 5×103 | 57.951 7 | 0.008 4 |
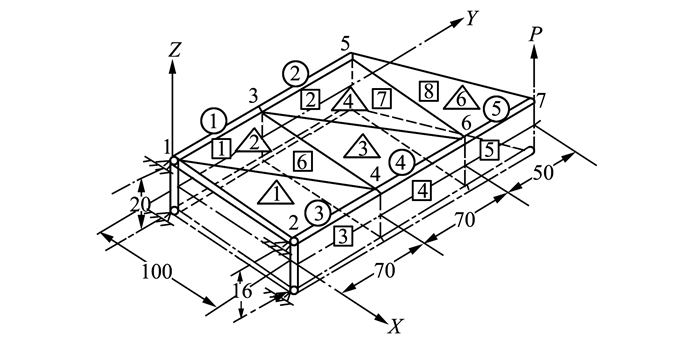
该算例来自文献[17], 如图 5所示为机翼翼盒结构, 该结构关于X-Y平面对称。
|
| 图 5 机翼翼盒结构示意图 |
在该结构优化问题中共有16个设计变量, 分别为5个杆件的横截面积, 3个受拉板的厚度以及8个剪切板的厚度。其中○为桁架杆, △为受拉板, □为受剪板。各设计变量均独立且不相关。其中杆件单元的横截面积取值范围为0.1~2.0 in2, 受拉板与受剪板的厚度取值范围均为0.02~1.00 in2。各单元所用材料相同, 其许用应力为10 000 lb/in2, 弹性模量为107 lb/in2, 材料密度为0.02 lb/in3, 泊松比为0.3。在节点1与节点2处X, Y, Z方向的位移边界条件为0。在节点7处受沿Z轴正向, 大小为5 000 lb的集中力。位移约束为各节点在Z方向上的位移均不得超过2 in, 应力约束为各单元许用应力为10 000 lb/in2。
因为本算例中设计变量较多, 故采用文中抽样策略抽样3 000次, 然后利用ICE-SVM方法对该机翼翼盒结构进行优化设计, 并与其他优化方法相比较, 得到的优化结果如表 4所示, 表 4中包括最优设计变量值与结构最小重量。
| 设计变量 | ACCESS1[17] | Gallatly & Berke[18] | Gallatly[19] | ICE-LSSVM |
| 桁架杆单元/in2 | ||||
| 1(1) | 4.045 0 | 0.650 5 | 1.043 1 | 0.314 5 |
| 2(2) | 0.100 1 | 0.100 1 | 0.103 6 | 0.100 3 |
| 3(3) | 0.100 1 | 0.236 6 | 0.350 8 | 0.882 4 |
| 4(4) | 0.133 0 | 0.235 6 | 0.331 5 | 0.602 2 |
| 5(5) | 0.100 2 | 0.100 1 | 0.103 5 | 0.100 2 |
| 受拉板单元/in | ||||
| 6(1, 2) | 0.082 86 | 0.132 8 | 0.144 1 | 0.048 5 |
| 7(3, 4) | 0.053 63 | 0.070 2 | 0.059 9 | 0.027 0 |
| 8(5) | 0.037 86 | 0.044 9 | 0.043 5 | 0.020 0 |
| 受剪板单元/in | ||||
| 9(1) | 0.363 6 | 0.087 6 | 0.087 6 | 0.020 0 |
| 10(2) | 0.223 6 | 0.088 9 | 0.089 5 | 0.020 0 |
| 11(3) | 0.131 0 | 0.080 8 | 0.066 4 | 0.054 7 |
| 12(4) | 0.115 6 | 0.076 8 | 0.055 3 | 0.061 7 |
| 13(5) | 0.091 66 | 0.081 5 | 0.053 7 | 0.052 9 |
| 14(6) | 0.020 00 | 0.020 0 | 0.021 9 | 0.020 0 |
| 15(7) | 0.020 00 | 0.020 0 | 0.021 5 | 0.020 0 |
| 16(8) | 0.030 96 | 0.033 7 | 0.025 6 | 0.020 0 |
| 重量(lb) | 80.589 1 | 77.537 8 | 42.104 8 | 35.470 7 |
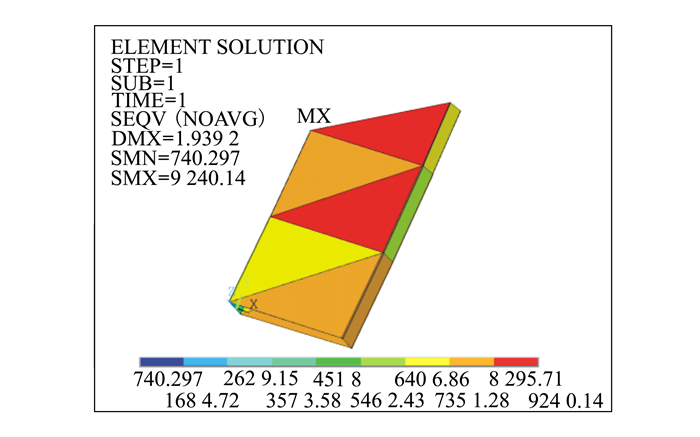
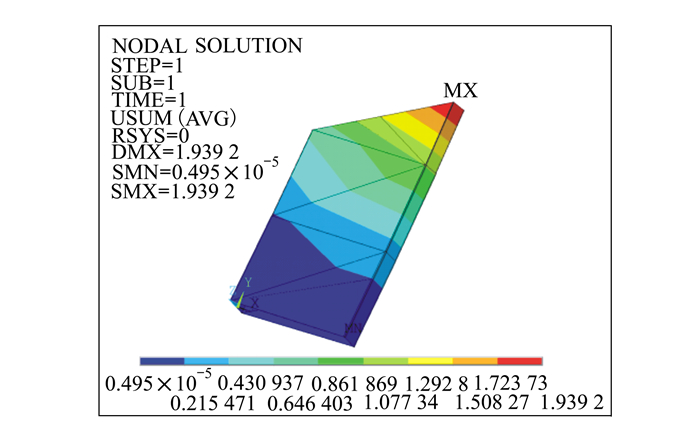
图 6与图 7分别为利用ICE-SVM方法所得到的最优设计变量, 在ANSYS中通过参数化建模分析得到的飞机翼盒结构节点应力与位移。从图 6、图 7可以看出, ICE-SVM方法给出的最优解均满足约束条件。ICE-SVM方法求得的飞机机翼翼盒结构最大应力和位移分别为9 240.14 lb/in2和1.939 2 in。
|
| 图 6 机翼翼盒结构应力云图 |
|
| 图 7 机翼翼盒结构的节点位移 |
针对工程优化设计中隐式函数和高计算量问题,本文采用支持向量机建立代理模型,讨论了在相同的抽样样本数下,不同抽样策略对代理模型精度的影响,选取在设计变量空间更为均匀的LCVT抽样构建更高精度的代理模型。在此基础上,本文提出了结合支持向量机与改进交叉熵算法的组合优化算法,改进交叉熵方法针对传统的交叉熵强调迭代速度牺牲计算精度的缺陷,提出了"全局精英样本"与"局部精英样本"的概念,通过保留历次迭代中的有用信息并将其应用于参数的更新中,适当降低算法的计算速度,而提高计算的精确度。另外还借鉴了"扰动函数"这一变异操作,避免了陷入局部最优。ICE-SVM方法保留了CE-SVM方法迭代速度快的特点,提高了计算精度与计算结果的鲁棒性。通过2个数值算例,1个工程算例,验证了ICE-SVM算法的可行性与有效性,对于飞机机翼等大型结构在优化过程中耗时过长的问题,ICE-SVM方法提供了一种有效的解决途径。
| [1] | Koroglu S A, Ergin A. A Decomposition Method for Surrogate Models of Large Scale Structures[J]. Journal of Marine Science and Technology, 2016, 21(2): 325-333. DOI:10.1007/s00773-015-0354-x |
| [2] | Vapnik V N. The Nature of Satistical Learning Theory[M]. Pringer, 1995: 988-999 |
| [3] | Suykens J A K, Vandewalle J. Least Squares Support Vector Machine Classifiers[M]. Kluwer Academic Publishers, 1999: 293-300. |
| [4] | Rubinstein R Y. Optimization of Computer Simulation Models with Rare Events[J]. European Journal of Operational Research, 1997, 99(1): 89-112. DOI:10.1016/S0377-2217(96)00385-2 |
| [5] | Rubinstein R. The Cross-Entropy Method for Combinatorial and Continuous Optimization[J]. Methodology and Computing in Applied Probability, 1999, 1(2): 127-190. DOI:10.1023/A:1010091220143 |
| [6] | Chepuri K, Homem De Mello. Solving the Vehicle Routing Problem with Stochastic Demands Using the Cross-Entropy Method[J]. Annals of Operations Research, 2005, 134(1): 153-181. DOI:10.1007/s10479-005-5729-7 |
| [7] | Santosa B. Application of the Cross-Entropy Method to Dual Lagrange Support Vector Machine[C]//International Conference on Advanced Data Mining And Applications, 2009 https://link.springer.com/chapter/10.1007%2F978-3-642-03348-3_61 |
| [8] | Ghidey H. Reliability-Based Design Optimization with Cross-Entropy Method[D]. 2015 https://brage.bibsys.no/xmlui/handle/11250/2349929 |
| [9] |
任超, 张航, 李洪双. 随机优化的改进交叉熵方法[J]. 北京航空航天大学学报, 2018, 44(1): 205-214.
Ren Chao, Zhang Hang, Li Hongshuang. Stochastic Optimization Method Based on Improved Cross Entropy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(1): 205-214. (in Chinese) |
| [10] | Rubinstein R Y. Cross-Entropy and Rare Events for Maximal Cut and Partition Problems[J]. ACM Trans on Modeling & Computer Simulation, 2002, 12(1): 27-53. |
| [11] | Rubinstein R Y. A Stochastic Minimum Cross-Entropy Method for Combinatorial Optimization and Rare-Event Estimation[J]. Methodology & Computing in Applied Probability, 2005, 7(1): 5-50. |
| [12] | Botev Z I, Kroese D P. The Generalized Cross Entropy Method with Applications to Probability Density Estimation[J]. Methodology & Computing in Applied Probability, 2007, 13(1): 1-27. |
| [13] | Romero V J. Comparison of Pure and "Latinized" Centroidal Voronoi Tessellation against Various Other Statistical Sampling Methods[J]. Reliability Engineering & System Safety, 2006, 91(10/11): 1266-1280. |
| [14] | Jones D R, Schonlau M, Welch W J. Efficient Global Optimization of Expensive Black-Box Functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. DOI:10.1023/A:1008306431147 |
| [15] | Liang J J, Runarsson T P, Mezura-Montes E, et al. Problem Definitions and Evaluation Criteria for the CEC 2006 Special Session on Constrained Real-Parameter Optimization[J]. International Journal of Computer Assisted Radiology & Surgery, 2005(2): 1-24. |
| [16] |
陈小前. 飞行器不确定性多学科设计优化理论与应用[M]. 北京: 科学出版社, 2013.
Chen Xiaoqian. Theory and Application of Uncertainty-Based Multidisciplinary Design Optimization for Flight Vehicles[M]. Beijin: Science Press, 2013. (in Chinese) |
| [17] | Schmit A L, Miura H. Approximation Concepts for Efficient Structural Synthesis[J]. AIAA Journal, 1976, 12(24): 8508-8523. |
| [18] | Gellatly R A, Berke L. Optimal Structural Design[R]. Flight Dynamics Laboratory, 1971 https://www.researchgate.net/publication/235105371_Optimal_Structural_Design |
| [19] | Gellatly R A. Development of Procedures for Large Scale Automated Minimum Weight Structural Design[R]. Flight Dynamics Laboratory, 1966 https://www.researchgate.net/publication/235018714_DEVELOPMENT_OF_PROCEDURES_FOR_LARGE_SCALE_AUTOMATED_MINIMUM_WEIGHT_STRUCTURAL_DESIGN |


