对于工程应用中大部分流动而言,准确描述和理解复杂流动结构变化和不稳定机理至关重要[1-2]。然而,即使近几十年来计算机技术的发展和实验测试仪器性能不断提升,要准确量化地提取复杂流动结构依然非常困难,且在对流动进行稳定性分析时,需要计算大型矩阵的逆和特征值,大型矩阵的计算代价依然比较昂贵。
在获得流动结构的众多方法中,本征正交分解方法(proper orthogonal decomposition, POD)被广泛使用[3]。POD方法是1种高效的降阶方法,其核心思想是寻找1组最佳的标准正交基,使得样本数据在该标准正交基上的投影依次迅速递减,截取投影较大(包含能量较高)的前几阶模态,从而可以用较少的基展开获得较高阶数据的近似描述。Lumley[3]首先将POD方法引入湍流研究以来,接着Sirovich[4]引入了snapshot方法来研究波动流的动力学问题。很多学者应用POD进行流动分析开展了大量的工作,发现使用较少的POD基就能准确捕捉到流场的演化特性。
较少的几个高阶POD模态就可以捕捉流动中的绝大部分能量,对于提取流场的主要特征或进行流场重构而言这是有利的1方面,然而,对于捕捉比较细致的流动结构而言,这又是1个不足之处。另1方面,目前大部分关于POD的研究都局限于不可压缩流动,POD方法研究应用在可压缩流动中的1个关键问题就是内积形式的选取,对于不可压缩流动而言,只有速度是重要的动力学参量,因此,速度场组成的矢量函数空间中标准内积的物理意义可以看作动能。然而,可压缩流动的N-S方程中,速度、热力学参数都为重要的动力学参量,在包含速度和热力学参量的矢量空间中,标准内积就失去了物理意义,因为从物理学的角度上来说,直接累加速度和温度是没有意义的。为解决此问题,Lumley等[5]介绍了1种加权形式的内积,该方法适用于较为均匀的湍流脉动,但其提取的“能量”不具有物理意义。Rowley等[6]提出1种兼顾能量方程和物理意义的内积形式,但是该方法只能应用于压缩性较弱的可压缩流动。
动力学模态分解(dynamic mode decomposition, DMD)是近年来从整体稳定性Koopman分析的基础上发展起来的1种低维系统分解的数学工具[7]。它只基于流动快照而不受流动类型的限制,其对流场的分解基于流场的动力学特性,所提取的子结构在时/空演化特性上相互正交,可以得到流动在时间和空间上的主要特征。DMD方法由Schmid等[7]首次提出,随后其将DMD方法分别对数值方法和实验得到的流场数据进行分析。Rowley等[8]采用DMD方法对横向射流中的非线性流动进行分析,结果表明,该方法可以提取主要的流动结构以及频率,通过与DNS、线化N-S方程、以及POD方法得到的频率进行对比,发现DMD得到频率与DNS的结果相同,而其他方法得到的频率均与DNS结果存在较大差距。Roy等[9]将DMD方法和POD方法应用于反应流的稳定性分析中,并对比了2种方法的结果。
圆柱绕流是流体力学的经典问题之一[10]。当Reynolds数较小时,流动是定常的,随着Reynolds数的逐渐增加,圆柱会出现一对尾涡,当Reynolds数较大时,尾涡首先失稳,出现周期性震荡,进而形成卡门涡街。本文分别采用DMD和POD方法对圆柱绕流卡门涡街发展历程中3个阶段流场的动力学特性进行分析,并对比2种方法的差异。
1 计算方法及验证算例二维非定常N-S方程在直角坐标系中的积分守恒形式为:
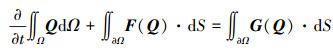
|
(1) |
式中,Ω为控制体, ∂Ω为控制体单元边界, Q为守恒变量, F(Q)为无黏通量, G(Q)为黏性通量, Q=
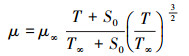
|
(2) |
式中,μ∞和T∞为远场的黏性和温度, S0=110 K。
采用有限体积方法进行空间离散, 空间格式采用Roe, 时间推进采用LU-SGS, 对于低雷诺的卡门涡街流动采用层流进行计算。
圆柱绕流的计算状态为Re=100, 本文圆柱绕流的计算网格采用多块结构化网格, 网格单元总数为38 818。为了保证非定常计算精度, 时间步长为0.1 s, 保证每个周期内大概有60~80个点。表 1为本文计算的升力系数幅值、阻力系数幅值和Strouhal数与文献[11-12]中结果的对比, 其中St=fD/U∞, 计算结果与文献结果吻合较好, 由此验证了本文计算方法的可靠性。
动态模态分解方法通过提取流动中的模态, 从而准确地描述流动结构。其数据来源是数值仿真或者物理实验, 以快照序列的形式呈现, 序列由矩阵V1N表示。
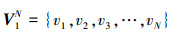
|
(3) |
式中, vi代表第i个流场, vi∈CM。在上述定义中, 下标1表示序列中的第1个元素, 下标N表示进入序列中的最后1个元素, 即矩阵V1N的第1列和最后1列, 我们可以假设这个序列的时间间隔为常量Δt。
第1步 假设线性映射A是快照vi到vi+1的映射, 即
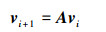
|
(4) |
且在全部区域和整个时间段内的采样都满足上述映射关系, 对于缓慢变化的系统, 乘法准则是上述假设的基础。
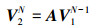
|
(5) |
系统矩阵A能够将时-空物理场沿时间维度平移Δt, 因此, A的特征值刻画了V1N的时间演化特性。然而, 实际应用中A是1个含有数据量极大的矩阵, 因此, 希望将A转化为1个小型矩阵, 用小型矩阵的特征值来估算A的特征值, 这样DMD方法才能应用于实际动力学问题。
对于秩为r的数据列V1N-1, A与其简化后的矩阵F可以通过V1N-1的POD模态联系起来
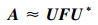
|
(6) |
式中,F∈Cr×r, U*为POD模态U的复共轭转置矩阵, U可以由V1N-1的奇异值分解得到, 即
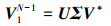
|
(7) |
式中, Σ是1个r×r的对角矩阵, 有非零的对角元素{σ1, …, σr}, 并且, U和V为酉矩阵。
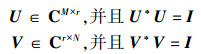
|
将(6) 式和(7) 式代入(5) 式中, 可得
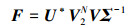
|
(8) |
F即为A的最优的低维估计矩阵, 由此, 通过求解F的的特征值和特征向量即可得到DMD分析结果。
假设F是1个r维子空间内的精确映射矩阵而不是对A的估计, 那么
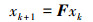
|
(9) |
则A的POD模态U可以看作从xk到vk的近似映射, 则
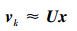
|
(10) |
如果F的特征向量个数与秩相等且都线性独立, 那么F可以写做如下形式
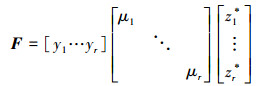
|
(11) |
式中,yi是其特征向量, μi为其特征值, 每1个yi的模为1个单位长度, yi*yi=1, zi*是F*的特征向量, F*的相应特征值为μi, zi*和yi满足如下的条件
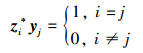
|
(12) |
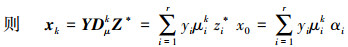
|
(13) |
式中, αi=zi* x0表示初始条件对第i个模态的影响程度, 所以, 可以利用DMD模态的线性组合来估计数据快照, 模态为Φi=Uyi, 则
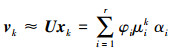
|
(14) |
由此可得
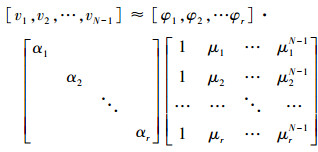
|
(15) |
(15) 式中αi为振幅, 它表示了初始条件对DMD模态在整个系统响应中起到的影响。如果αi值比较大, 那么说明其对应的DMD模态对于选取的初始条件的作用较大。动态模态分解获得的最重要结果是模态φi和模态对应的特征值μi, log μi/Δt的实部为对应模态的放大率, 其虚部表示对应模态的频率, 在进行稳定性判断时, 放大率为正, 则对应的模态不稳定, 放大率为负, 则对应的特征值稳定, 若放大率为零, 则对应的模态为周期性模态。
3 POD方法POD方法的核心思想是从1组时间序列的空间数据中寻找在均方意义上的最优正交基函数空间, 用较少正交基展开获得较高阶数据的近似描述, 具体推导过程如下。
选取N个瞬态速度场, 定义vi代表第i个速度场, 选取数据库中N个的时刻瞬态速度场V1N构成快照集合, 将快照写成平均值与脉动量的和
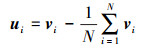
|
(16) |
利用V1N构成1组时间序列的空间数据集合, 寻找1组最优正交基{Φi|i=1, 2, …N}建立映射Φ:RN→S, 使得原系统与投影在正交基上的降维系统误差最小
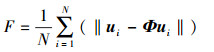
|
(17) |
这一问题等价于使得正交基函数满足最大值问题
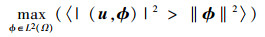
|
(18) |
式中,L2(Ω)是定义在空间区域Ω上的L2函数空间; (·, ·)表示该函数空间上的内积; ‖Φ‖2=(Φ, Φ)1/2; 〈·〉表示算术平均运算。
利用变分法, 该最大值问题可转化为特征值问题
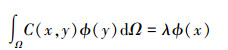
|
(19) |
式中,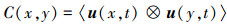
由于实际应用中快照都是在离散空间点上的实验数据或数值模拟结果, 这时的自相关函数可以表示为

|
(20) |
本文采用Sirovich等[4]提出的快照技术(snapshots)求解POD模态, 该方法的主要思想是利用原函数空间元素与特征值问题中的特征模态处在同一线性空间中, 从而可以利用原有函数空间快照的线性组合来表示特征模态, 即
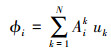
|
(21) |
将(21) 式代入(19) 式中, 得到

|
(22) |
式中,Ai为对应特征值λi的特征函数
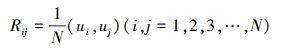
|
(23) |
所需求解的特征值问题只有N阶, 远小于空间点M的量级, 即可通过求解相关矩阵R的特征值和特征向量得到POD模态。
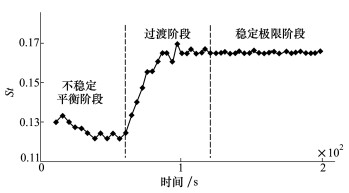
4 计算结果分析图 1为St随时间的变化, 根据St的变化, 可将流场中卡门涡街发展过程划分为3个阶段, 分别为:0~60 s为不稳定平衡态阶段, 60~120.5 s为过渡阶段, 120.5~200 s为稳定极限环阶段。
|
| 图 1 St随时间的变化 |
本文分别采用DMD和POD方法对圆柱绕流卡门涡街发展历程中3个阶段的动力学特性进行分析。分别在每个阶段提取2个周期的非定常速度场数据样本, 2个周期的数据已可以分析到流场结构的主要特征, 3个阶段取样的时间范围分别为:15.6~33.3 s、68.8~83.2 s、134.1~147.7 s。
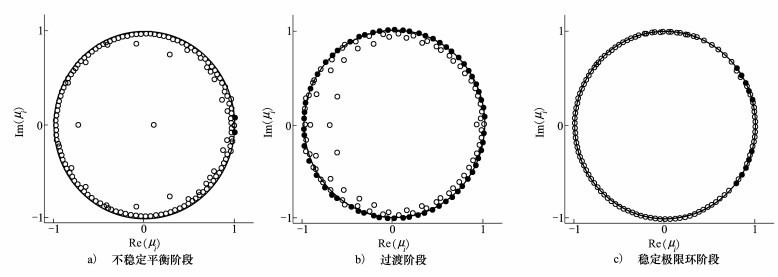
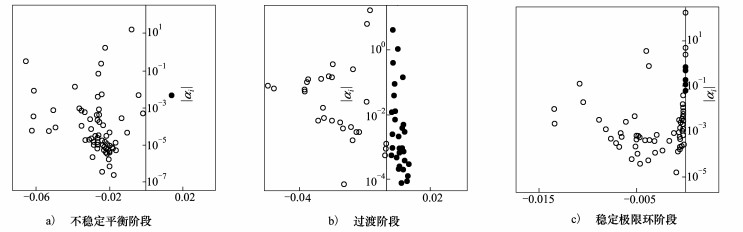
4.1 DMD计算结果及分析图 2为3个阶段DMD特征值的实部和虚部在单位圆上的分布, 其中横轴为实部, 纵轴为虚部。空心点表示在单位圆上或单位圆内, 实心点表示在单位圆外, 空心点对应稳定模态或周期性模态, 而实心点对应不稳定模态。图 3为3个阶段下为模态幅值与放大率之间的关系, 实心点的表示放大率正, 对应模态系数发散, 空心点表示放大率为负或零, 对应模态系数收敛或呈现极限环状态。
|
| 图 2 特征值的实部与虚部在单位圆上的分布 |
|
| 图 3 放大率与幅值之间的关系 |
可以看出, 在不稳定平衡阶段, 绝大部分的模态为稳定模态, 放大率为负, 其中有3个模态对应的放大率绝对值较小, 且均在单位圆附近, 说明其为对应衰减缓慢的周期性模态。而其他模态衰减较快, 不稳定模态仅有2个, 由图 3可知这2个模态为共轭模态, 实际是1个模态, 其对应的放大率较大, 均为1.398 913 4×10-2。
在过渡阶段, 总模态数为144个, 其中不稳定模态有64个, 不稳定模态较多, 其中放大率最大为1.023 893 7×10-2, 稳定模态中大部分对应的放大率绝为对值较小, 且均在单位圆附近, 说明其为对应衰减缓慢的周期性模态。
在稳定极限环阶段, 从图 2中可以看出, 基本上所有的的特征值均非常靠近单位圆, 几乎落在单位圆上, 说明所有的模态均为周期性模态, 其中不稳定模态为8个, 由于均呈现共轭出现, 所以实际上只有4组, 且其放大率最大为3.191 359 3×10-5, 比第1个阶段和第2个阶段中最大的放大率小了3个数量级, 其对应的模态为弱不稳定周期性模态。
对不稳定平衡阶段进行DMD分析, 按照模态系数幅值绝对值的大小进行排序, 提取前5阶模态和仅有的1阶不稳定模态进行分析, 表 2为提取模态的频率以及放大率, 1阶模态的放大率最小, 比其他模态放大率小了2~3个量级, 其系数在整个时间段内的变化不到1%, 其为流场的主要模态, 2阶模态的变化快于1阶模态。3阶、4阶、5阶模态的系数基本收敛到零, 说明虽然在起始阶段其在整个流场中的作用较大, 但是其衰减的速度很快, 在最终时刻对流场影响很小。6阶模态为发散模态, 其系数初值较小, 但对应的放大率为正且较大, 因此, 虽然在起始阶段其在整个流场中的作用较小, 但是其发散的速度很快, 说明6阶模态非常不稳定, 流动从平衡阶段发展到过渡阶段6阶模态起到了主导作用, 其发散的St为0.125 543 7。同时, 对升力系数在此阶段进行FFT分析, 其主频对应的St为0.124 866, 这与DMD方法提取的发散St之间的差距仅为0.5%, 说明对于圆柱不稳定平衡阶段, DMD分析方法可以准确提取其不稳定的流场模态结构及相应频率。
| 模态数 | St | 放大率 |
| 1 | 0.000 000 0 | -5.561×10-5 |
| 2 | 0.008 890 8 | -0.008 200 2 |
| 3 | 0.044 512 1 | -0.022 743 2 |
| 4 | 0.286 867 6 | -0.065 565 2 |
| 5 | 0.125 543 7 | -0.024 839 0 |
| 6 | 0.126 543 0 | 0.013 989 1 |
对过渡阶段DMD分析结果中前6阶模态进行分析, 表 3为模态频率以及放大率, 可以看出, 前4阶模态稳定, 1阶模态的放大率比其他模态小3个量级, 其系数在整个时间段内的变化不到0.03%, 其为流场的主要模态, 2阶模态的变化快于1阶模态, 3阶模态系数收敛较快, 4阶模态系数在振荡中趋于收敛, 5阶模态和6阶模态均为发散模态。对升力系数在此阶段进行FFT分析, 其主频对应的St为0.153 211 1, 5阶模态的St为0.154 480 6, 2者相差为0.8%, 6阶模态的St为0.308 526, 是升力系数主频对应St的2倍, 说明对于圆柱过渡阶段, DMD分析方法依然可以准确地提取主要的流场模态结构及相应频率, 且可分析其稳定性。
| 模态数 | St | 放大率 |
| 1 | 0.000 000 0 | -2.156×10-6 |
| 2 | 0.000 000 0 | -0.007 745 7 |
| 3 | 0.000 000 0 | -0.080 374 7 |
| 4 | 0.128 426 9 | -0.009 126 3 |
| 5 | 0.154 480 6 | 0.002 693 7 |
| 6 | 0.308 526 8 | 0.005 325 9 |
对极限环阶段DMD分析结果中前2阶以及之后4阶高阶模态进行分析, 表 4为提取模态的频率以及放大率, 图 4为模态速度云图。可以看出, 1阶模态的频率为0, 放大率极小, 其为流场的主要结构, 由验证算例可知, Re=100时, 卡门涡街涡脱落的St为0.163 624, 记为St0, 2阶模态的St为0.164 786, 2者相差0.7%, 且其对应的模态流场速度云图存在明显的交替出现速度结构, 其为脱落涡的主要模态。3阶至6阶模态的St分别为2St0、3St0、4St0、5St0, 其中虽然3阶、4阶和5阶模态为不稳定模态, 但是其放大率非常小, 幅值几乎不变。因此, 说明DMD方法可以非常准确地提取卡门涡街脱落涡中主要结构和高阶谐波模态, 且可分析其稳定性。

|
| 图 4 稳定极限环阶段DMD模态速度云图 |
| 模态数 | St | 放大率 |
| 1 | 0.000 000 0 | -9.482 7×10-8 |
| 2 | 0.164 786 2 | -1.112 0×10-5 |
| 3 | 0.329 657 1 | -6.346 2×10-7 |
| 4 | 0.494 421 9 | 1.029 6×10-5 |
| 5 | 0.659 222 4 | 7.159 7×10-6 |
| 6 | 0.824 008 8 | 1.888 2×10-5 |
采用POD方法分别对3个阶段进行分析, 模态能量比按下式计算
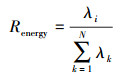
|
(24) |
式中,λi为第i阶模态对应的特征值。
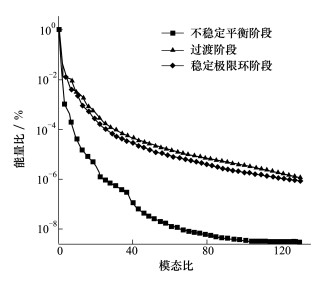
图 5为模态能量比的分布, 可以看出, 能量比衰减非常快, 前15阶的模态所占的能量已经达到了总能量的99%, 已经可以较为精确地重构流场。按能量比的大小对模态进行排序, 提取前6阶模态进行分析。
|
| 图 5 3个阶段下POD模态能量比分布 |
表 5为前6阶POD模态系数进行FFT分析得到的St以及相应的能量比。表中过渡阶段的4阶、5阶和6阶以及稳态极限环阶段的6阶频率中存在2个频率, main表示主频, second表示次频。可以看出, 3个阶段中第1阶模态系数的St均为0, 且模态系数几乎不变, 其能量比非常大, 分别为97.552%, 85.974%, 87.052%, 尤其是在第1阶段, 1阶模态几乎占据了流场的绝大部分的能量, 因此, 1阶模态为流动结构中最主要的稳定模态。
| 模态数 | 不稳定平衡阶段 | 过渡阶段 | 稳定极限环阶段 | |||||
| St | Renergy/% | St | Renergy/% | St | Renergy/% | |||
| 1 | 0.000 00 | 97.552 | 0.000 00 | 85.974 | 0.000 00 | 87.052 | ||
| 2 | 0.062 77 | 1.905 0 | 0.1543 3 | 3.456 0 | 0.163 44 | 3.892 0 | ||
| 3 | 0.062 77 | 0.308 0 | 0.154 33 | 3.177 0 | 0.163 44 | 3.712 0 | ||
| 4 | 0.062 77 | 0.094 0 | main:0.077 11 second:0.308 66 |
1.313 0 | 0.326 77 | 1.276 0 | ||
| 5 | 0.126 55 | 0.051 0 | main:0.308 66 second:0.077 11 |
1.149 0 | 0.326 77 | 1.241 0 | ||
| 6 | 0.126 55 | 0.035 0 | main:0.308 66 second:0.077 11 |
1.120 0 | main:0.081 66 second:0.245 11 |
0.452 0 | ||
不稳定平衡阶段中5阶和6阶模态系数的St为0.126 555, 这与流场不稳定频率对应的St之间相差1.35%, 略低于DMD方法提取频率的精度, 能量比均较小。
过渡阶段中2阶和3阶模态系数的St为0.154 333, 这与流场不稳定频率对应的St之间相差0.7%, 4阶、5阶和6阶模态的St中均存在0.308 666, 此St为不稳定St的2倍, 但这3个模态中又同时存在0.077 111的St, 且在不同的模态中, 这2个St作为主频和次频的顺序不同, 说明这3个模态中存在高频谐波模态和低频率模态耦合的现象, 并且高频模态与低频模态在不同模态中的主导作用不一样。这与DMD方法中1个模态对应1个频率有所区别, 说明在对流场结构的频率进行提取和分析时, DMD方法更具有优势。
稳定极限环阶段中2阶和3阶模态系数的St为0.163 444, 这与流场不稳定频率对应的St之间相差0.7%, 4阶, 5阶模态的St均为0.326 77, 此St为不稳定St的2倍, 为高频谐波模态。6阶模态也存在2个低阶频率。
图 6为3种阶段下POD模态速度云图, 与DMD模态速度云图相比, POD模态速度云图更加光滑有序。

|
| 图 6 稳定极限环阶段POD模态速度云图 |
本文重点分析极限环阶段中2种方法得到的模态结构的差异。对于1阶模态而言, DMD模态和POD模态的结构一样, 仅仅相差1个正负号, 反映了时间平均下的流动结构。对于2阶模态而言, DMD模态和POD模态的结构一样, 相对于DMD模态, POD模态在速度值上进行放大, 模态速度云图中圆柱的尾迹区存在沿x方向规律的交替出现, 且沿x轴上下反对称的速度结构。
对于3阶模态而言, 2种方法的结果存在差异, DMD模态的频率为脱落涡主频的2倍, 对应的流动结构发生了变化, 沿x方向交替出现, 且沿x轴呈现上下对称的速度结构, 速度幅值变小。而POD模态的频率依然为脱落涡的主频, 且其流动结构与2阶模态一样, 两者之间仅相差正负号和幅值的缩放。
对于3阶以上的模态而言, DMD模态的频率为脱落涡主频的倍数, 速度结构规律明显, 对应的流动结构沿x方向交替出现, 且沿x轴呈现上下对称或反对称的速度结构, 且随模态阶数的增加速度结构逐渐变小。POD的4阶模态的流动结构与DMD的3阶模态非常类似, 2者对应的St也比较接近。POD的5阶模态与自身的4阶模态的比较接近, 频率相同。
根据上述采用DMD和POD方法对圆柱绕流卡门涡街发展的3个阶段的稳定性分析的结果可知,POD方法可以高效地提取流场的主要结构,很少数量的POD模态就占据了流场的主要能量,且通过对模态系数进行FFT分析,可以得到模态的频率,其可以高效得到流场空间上的主要特征。DMD方法不仅可以提取流场的主要结构,直接得到模态对应的频率,且可以判断其稳定性,即是可以同时得到流场在空间和时间上的主要特征。从动力学分析的角度讲,相比于POD方法,DMD方法可以得到关于动力学系统的更多信息。
且由于构造的内积的缺陷,现阶段POD方法还主要用在不可压缩和弱可压缩的流动中,对于高速可压缩流动,合理内积的构造还是一个尚未彻底解决的问题。而DMD方法是只基于流动快照数据而不受流动类型和条件的限制。因此,在流动类型的适应范围上,DMD更加具有优势。
5 结论本文分别将DMD和POD方法应用在圆柱绕流卡门涡街发展中3个阶段流动的稳定性分析中,并对比2种方法各自的特点,得到以下结论:
1) DMD方法可以准确提取卡门涡街中脱落涡发展过程中的主要的不稳定流场模态以及频率,对于稳定极限环阶段,不仅可以提取主要的脱落涡结构,和较多的高阶谐波模态,还可以判断所有提取模态的稳定性。
2) POD方法可以高效地提取流场中的主要流动结构,模态的能量比衰减的很快,通过对其模态系数进行FFT分析,可以得到对应的频率,但存在多个频率耦合的模态,且POD方法无法判断所提取模态的稳定性。
3) 对比DMD和POD方法,DMD方法不仅可以提取流场的主要结构,直接得到模态及对应的频率,且可以判断其稳定性,因此DMD方法可以同时得到流场在空间和时间上的主要特征。POD方法可以高效得到流场在空间上的主要特征。且由于构造的内积的缺陷,DMD可以应用的流动类型范围比POD的范围更宽。
因此,在对复杂动力学系统进行稳定性分析时,DMD方法更具优势。
| [1] | Theofilis V. Global Linear Instability[J]. Annual Review of Fluid Mechanics, 2011, 43: 319-352. DOI:10.1146/annurev-fluid-122109-160705 |
| [2] | Gómez F, Clainche S L, Paredes P, et al. Four Decades of Studying Global Linear Instability: Problems and Challenges[J]. AIAA Journal, 2012, 50(12): 2731-2743. DOI:10.2514/1.J051527 |
| [3] | Lumley J L. The Structure of Inhomogeneous Turbulence Flows[C]//Atmospheric Turbulence and Radio Wave Propagation. Moscow, Nauka, 1967: 166-176 |
| [4] | Sirovich L. Turbulence and the Dynamics of Coherent Structures[J]. Parts Ⅰ-Ⅲ Quarterly of Applied Mathematics, 1987, XLV(3): 561-582. |
| [5] | Lumley J L, Poje A. Low-Dimensional Models for Flows with Density Fluctuations[J]. Physics of Fluids, 1997, 9(7): 2023-2031. DOI:10.1063/1.869321 |
| [6] | Rowley C W, Colonius T, Murray R M. Model Reduction for Compressible Flows Using POD and Galerkin Projection[J]. Physica D Nolinear Phenomena, 2003, 189: 115-129. |
| [7] | Schmid P J. Dynamic Mode Decomposition of Numerical and Experimental Data[J]. Journal of Fluid Mechanical, 2010, 656: 5-28. DOI:10.1017/S0022112010001217 |
| [8] | Rowley C W, Mezic I, Bagheri S, et al. Henningson D Spectral Analysis of Nonlinear Flows[J]. Journal of Fluid Mechanical, 2009, 641: 115-127. DOI:10.1017/S0022112009992059 |
| [9] | Roy S, Hua J C, Barnhill W, et al. Deconvolution of Reacting-Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions[J]. Physical review E, 2015, 91: 013001. DOI:10.1103/PhysRevE.91.013001 |
| [10] |
酆庆增. 圆柱绕流的非线性动力学[J]. 力学进展, 1994, 24(4): 525-546.
Feng Qingzeng. Nolinear Dynamics of Viscous Flows Past a Circular Cylinder[J]. Advances in Mechanics, 1994, 24(4): 525-546. DOI:10.6052/1000-0992-1994-4-J1994-049 (in Chinese) |
| [11] | Tritton D J. Experiments on the Flow Past a Circular Cylinder at Low Reynolds Numbers[J]. Journal of Fluid Mechanics, 1959, 6(4): 547-567. DOI:10.1017/S0022112059000829 |
| [12] | Lu L, Qin J M, Teng B, et al. Numerical Investigations of Lift Suppression by Feedback Rotary Oscillation of Circular Cylinder at Low Reynolds Number[J]. Physics of Fluids, 2011, 23(3): 033601. DOI:10.1063/1.3560379 |


