机械产品的动态可靠性是指其在给定的时间区间上能够正常运行的概率[1]。输入的不确定性必然导致实际输出具有不确定性, 而输出的不确定性在一定程度上便会导致机械产品的破坏。可靠性分析能够得到输出响应量的统计规律, 从而能够衡量机械产品安全运行的概率, 为保证产品的安全提供参考。
目前, 已经形成的比较有效的求解机械产品可靠性方法包括一次可靠性方法(FORM)[2-3]、改进的一次可靠性方法(FOSM)[4-5]和蒙特卡罗方法(MCS)等[6]。蒙特卡罗法虽然对功能函数的形式及变量的概率密度函数和维数没有限制且一般精度较高, 但其计算量巨大。改进的一次方法能够很好地权衡计算精度和计算效率, 本文在该方法基础上研究时空动态可靠性及其全局灵敏度分析的高效方法。对于工程中常见的输入变量变异性较小的问题, 该类方法具有较高的精度。
对于动态可靠性问题, 目前使用较多的方法可以分为2类:基于极值响应的方法[7-9]和基于首次超越的方法[10-11]。基于极值响应的方法针对极值分布可求得的情况, 其能够将动态可靠性问题转变为静态可靠性问题进行求解。目前基于首次超越的思想方法中使用较多的方法是使用Rice公式[12], 但获得跨越率依然很难。
包络函数法常应用于电子工程领域[13], 有学者[14-15]将包络函数法应用于结构优化问题。Du[16]提出了动态可靠性分析问题的包络函数法, 能够很好地克服以上动态可靠性方法的缺点。该方法通过引入失效边界上失效概率最大点处的包络面来近似失效域, 从而将动态可靠性问题转化为扩展点处的静态可靠性问题。由于该方法只针对包含一维参数的动态可靠性问题, 因此并不能用来分析多参数动态可靠性问题。
可靠性全局灵敏度分析可以得到影响产品可靠性的输入变量的重要性, 如静态问题的可靠性全局灵敏度分析[17]。为了能够分析得到影响机械产品动态可靠性的基本输入变量的重要性, 十分有必要研究动态可靠性的全局灵敏度分析方法。
本文在文献[16]基础上提出一种计算含有时间和空间多维参数的动态可靠性问题的包络函数法, 该方法能够很好地克服以上方法的缺陷, 得到较为准确的结果。对于多输出的问题, 该方法亦具有一定的适用性。同时, 在该可靠性方法的基础上, 本文结合三点估计提出了一种计算可靠性全局灵敏度指标的新方法。
1 时空动态可靠性分析定义时间t和空间z的多参数的动态输出响应为f(x, z, t)。其中, x=(x1, …, xn)是n维随机输入变量, z∈[z0, zf]是空间位置参数, t∈[t0, tf]是时间参数。为了保证机械产品能够正常工作, 要求输出响应必须不大于要求的阀值ε。因此, 多参数动态可靠性定义为在给定的时间和空间内输出响应满足要求阀值的概率, 定义式如下
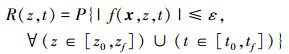
|
(1) |
而失效概率则定义为至少存在一个时刻或者空间位置使输出响应大于阀值的概率, 即
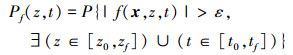
|
(2) |
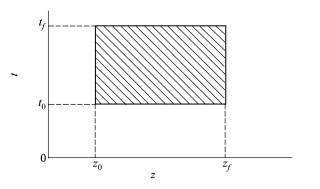
式中, 并集(z∈[z0, zf])∪(t∈[t0, tf])表示时间与空间组成的参数取值域, 若以z为横坐标, t为纵坐标, 则其表达为图 1中的矩形域。
|
| 图 1 参数取值空间 |
分别使用F1(x)=0和F2(x)=0作为随时间t和空间z连续变化的动态失效边界f(x, z, t)=ε和f(x, z, t)=-ε上的包络函数, 首先考虑正的失效边界f(x, z, t)=ε的包络函数F1(x)=0。f(x, z, t)=ε可以看作是当参数z和t在其区间变化时的一系列随机输入变量空间上的超曲面。
考虑空间和时间的2个邻近超曲面分别为f(x, z, t)=ε与f(x, z+δz, t)=ε及f(x, z, t)=ε与f(x, z, t+δt)=ε, 其中δz>0, δt>0, 则有
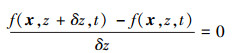
|
(3) |
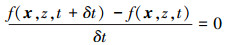
|
(4) |
当δz和δt无限趋近于零时, 可以得到如下的偏微分方程
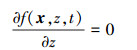
|
(5) |
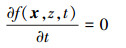
|
(6) |
上述两式可以简单记为如下形式

|
(7) |
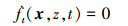
|
(8) |
理论上, 通过求解以上2个偏微分方程可以得到空间参数z和时间参数t关于输入变量x的函数, 记(7) 式和(8) 式的解为z=h1(x)和t=h2(x), 并将z和t的解代入f(x, z, t)-ε=0便可以得到正失效边界包络函数F1(x)的表达式如下
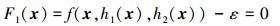
|
(9) |
同理可以求得负失效边界的包络函数表达式F2(x), 此时动态可靠性问题转化成如下的形式
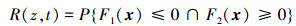
|
(10) |
由上面的公式可以看出, 动态可靠性的求解已经被转化成一个静态可靠性的问题。以下将结合一次可靠性的近似方法来估计包络函数。
2.2 包络函数的估计假设输入变量相互独立且均服从正态分布, 对于输入变量非正态或相关的情况可以使用R-F方法与Rosenblatt方法[6]将其转化成正态变量。在输入变量变异性较小的基础上使用一阶泰勒公式将输出响应函数在输入变量均值处进行线性展开[6]
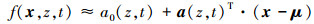
|
(11) |
式中, μ=(μ1, …, μn)T表示输入变量x的均值向量, a0(z, t)和a(z, t)分别由下式决定
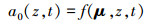
|
(12) |
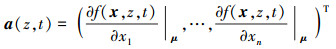
|
(13) |
为了简化运算, 将随机输入变量x转化为标准正态变量u
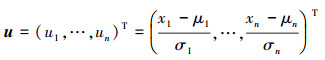
|
(14) |
式中,σ=(σ1, …, σn)T为x的标准差列阵。则(11) 式可以改写成如下形式
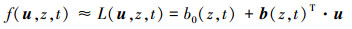
|
(15) |
式中, b0(z, t)和b(z, t)分别为
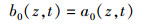
|
(16) |
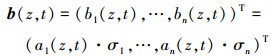
|
(17) |
到此, 就把原求解包络函数的问题转化为分别求解线性函数族L(u, z, t)=ε和L(u, z, t)=-ε的包络函数F1(u)=0和F2(u)=0的问题。
首先考虑正失效边界的包络函数F1(u)=0, 结合(7) 式和(8) 式, 其可以由下式决定
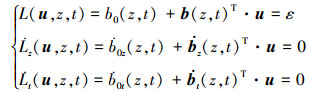
|
(18) |
式中, 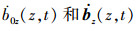
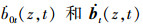
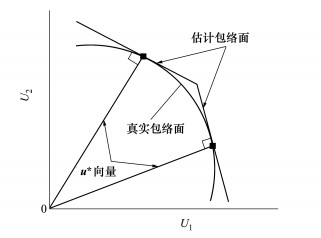
由包络函数的意义可知, 包络函数应该在参数区间[z0, zf]和[t0, tf]上包含所有的失效域。则包络函数F1(u)=0上的扩展点应该在线性函数L(u, z, t)=ε上, 并且在失效边界上具有最大的概率密度。假定u*为包络函数上的扩展点, 则u*为线性函数L(u, z, t)=ε上离原点最近的点。因此, u*向量与线性函数L(u, z, t)=ε相互垂直, 即u*与线性函数L(u, z, t)=ε在u*处的梯度共线。如图 2所示在标准正态空间下, 小方点即为扩展点。
|
| 图 2 估计包络面与真实包络面关系图 |
据该性质可得以下等式
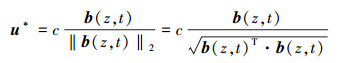
|
(19) |
式中, c为常数, 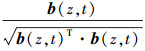
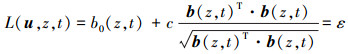
|
(20) |
通过以上等式可以解得常数c的值如下
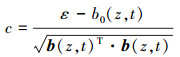
|
(21) |
将常数c的值代入(19) 式可得扩展点的值为
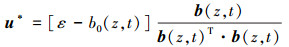
|
(22) |
将求得的扩展点代入(18) 式的第二和第三个等式得到关于参数z和t的方程组如下
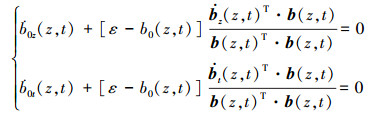
|
(23) |
通过求解以上方程组, 便可以得到参数z和t的一组解。由于此时是对应正失效边界包络函数进行求解, 因此其输出响应必为正值。将求得的解代入(12) 式计算均值输出, 排除掉对应均值输出为负值的解, 并且将最后得到的参数值记为(zi(1), ti(1))(i=1, 2, …, m1), 则扩展点为
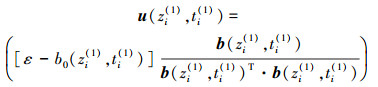
|
(24) |
同理, 对应负失效边界的包络函数F2(u)=0, 可求得其对应的参数值解为(zj(2), tj(2))(j=1, 2, …, m2), 其扩展点为
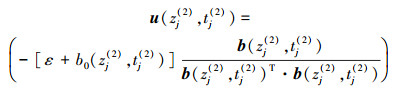
|
(25) |
此时, 正失效边界包络函数F1(u)=0就可以使用超平面L(u, zi(1), ti(1))=ε来估计, 其中i=1, 2, …, m1; 负失效边界包络函数F2(u)=0可以使用超平面L(u, zj(2), tj(2))=-ε来估计, 其中, j=1, 2, …, m2。结合(10) 式可知, 求解可靠性此时转化为如下形式
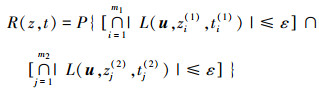
|
(26) |
上述包络面考虑了空间和时间参数分别在给定区间[z0, zf]与[t0, tf]内变化的情况, 其空间与时间边界以及端点处的情况也需要考虑。考虑响应在时间和空间参数区间4个边界上包络函数的情况, 即在边界(z∈(z0, zf), t0), (z∈(z0, zf), tf), (z0, t∈(t0, tf))和(zf, t∈(t0, tf))上求解其正负失效边界包络函数对应的参数解。此时, 问题相当于求解单参数动态可靠性的问题, 详细过程可参考文[16]。使用文[16]中单参数包络函数法求得4个边界上的包络函数F1(u)=0的m′1个参数解(zi(1), ti(1))(i=m1+1, m1+2, …, m1+m′1); 以及包络函数F2(u)=0的m′2个参数解为(zj(2), tj(2))(j=m2+1, m2+2, …, m2+m′2)。最后还需要引入参数区间端点的包络函数, 考虑响应在参数区间端点处的情况, 则需要分别加上(z0, t0), (z0, tf), (zf, t0)和(zf, tf)处的失效边界L(u, z*, t*)(其中z*为z0或zf, t*为t0或tf)。
令(z1*, t1*)=(z0, t0), (z2*, t2*)=(z0, tf), (z3*, t3*)=(zf, t0), (z4*, t4*)=(zf, tf), 则考虑所有端点及边界后原时空动态可靠性问题可简化为

|
(27) |
由于(27) 式的每一个极限状态方程均是线性正态的, 因此可以先求解所有等价输出的联合概率密度函数, 然后再由数值积分法求得可靠度。此处使用多元正态分布函数Φm(ε, μ, Σ)来求解(27) 式中的可靠性问题, 其中μ和Σ分别为均值向量和协方差向量。引入如下指示函数

|
(28) |
式中, i=1, 2, …, m1+m′1, j=1, 2, …, m2+m。考虑正失效边界包络面上发生负向失效(即其值小于-ε)与负失效边界包络面上发生正向失效(即其值大于ε)的可能性较小, 可将(27) 式写成如下形式。
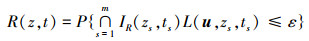
|
(29) |
式中, m=m1+m′1+m2+m′2+4。则可通过如下积分求解该动态可靠性问题。

|
(30) |
式中, 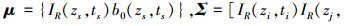
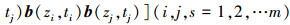
综合上述包络函数求解时空动态可靠性的过程, 其主要步骤可以给出如下:
步骤1 通过(23) 式求得正失效边界包络函数对应的参数值解, 并代入(12) 式计算均值输出, 剔除掉对应均值输出为负值的解, 最后得到参数值解(zi(1), ti(1))(i=1, 2, …, m1); 同理计算出负失效边界包络函数对应的参数值解(zj(2), tj(2))(j=1, 2, …, m2)。
步骤2 计算时间和空间参数边界以及端点对应的包络函数。
步骤3 采用数值积分或是数字模拟等方法求解时空动态可靠性问题的近似解, 此处采用(30) 式来求解时空多参数动态可靠性。
2.4 计算多输出时空动态可靠性考虑如下所示的多参数多输出串联响应问题
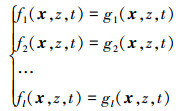
|
(31) |
式中, l为输出响应的个数。分别对上式左边输出响应函数fk(x, z, t)(k=1, 2, …, l)在输入变量均值处进行一阶泰勒展开并对输入变量标准正态化
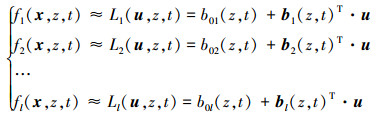
|
(32) |
式中, b0k(z, t)和bk(z, t)(k=1, 2, …, l)的定义如(16) 式和(17) 式所示, u的定义见(14) 式。
使用包络函数法求解多输出问题的步骤与以上求解单输出问题的步骤类似。使用(18)~(25) 式分别计算输出响应fk(x, z, t)(k=1, 2, …, l)在失效边界上对应的参数解。以m1(k)+m′1(k)和m2(k)+m′2(k)分别表示第k(k=1, 2, …, l)个输出Lk(u, z, t)≤ε和Lk(u, z, t)≥-ε所对应的参数解(zi(k1), ti(k1))(i=1, 2, …, m1(k)+m′1(k))和(zj(k2), tj(k2)) (j=1, 2, …, m2(k)+m′2(k))的个数, 且令端点的参数解为(z1(k)*, t1(k)*)=(z0, t0), (z2(k)*, t2(k)*)=(z0, tf), (z3(k)*, t3(k)*)=(zf, t0)和(z4(k)*, t4(k)*)=(zf, tf) (k=1, 2, …, l)。由于是串联系统, 则其总的可靠性为每个输出响应均安全时对应的可靠性, 即多输出的可靠性可以表示成如下形式

|
(33) |
由(33) 式可以看出, 多输出时空动态可靠性问题此时已经被转化为静态的可靠性问题, 其值可采用显式极限状态函数的可靠性求解的数值积分或数字模拟来求得。
3 动态可靠性全局灵敏度分析的包络函数法 3.1 方法思路对于一个动态可靠性的问题, 其失效域定义为
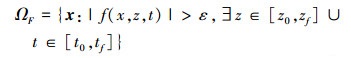
|
(34) |
由文献[17]可知, 输入变量对失效概率Pf影响的可靠性全局灵敏度因子可以定义为
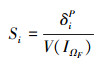
|
(35) |
式中
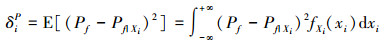
|
(36) |
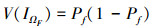
|
(37) |
式中, Pf表示机械产品的失效概率, Pf|Xi表示Xi取其实现值时的失效概率, E(·)和V(·)分别为期望算子和方差算子, IΩF为失效域指示函数, 当x∈{ΩF}时, IΩF(x)=1, 否则IΩF(x)=0。且对(36) 式经过进一步证明可得[18]
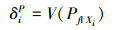
|
(38) |
由上式可以看出, δiP的求解包含两部分, 即内层条件失效概率和外层方差的求解。
本文将在统计矩方面具有较强优越性的三点估计法[19]和包络函数法结合起来计算可靠性全局灵敏度指标。根据三点估计法, 可以得到动态失效概率Pf和δiP如下[6, 20]:
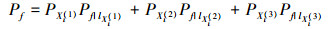
|
(39) |
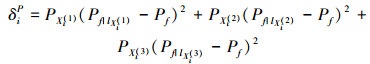
|
(40) |
式中, lXi(k)和PXi(k)(k=1, 2, 3) 分别为三点离散分布的取值点和相应的概率值[20], 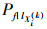
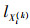
步骤1 通过文献[20]中公式分别求得三点离散分布的取值点和相应的概率值, 即lXi(k)和PXi(k)(k=1, 2, 3)。
步骤2 分别将变量Xi固定在名义值处, 即令Xi(k)=lXi(k), 然后使用包络函数法计算其条件失效概率值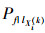
步骤3 将步骤2中得到的条件失效概率值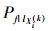
步骤4 将步骤3中求得的Pf和δiP的值代入(35) 式, 便可以得到可靠性全局灵敏度指标Si的值。
4 算例 4.1 悬臂梁如图 3所示为一长方体悬臂梁结构, 其横截面宽为b, 高为h。受力形式如图所示, 其中, 不规则分布载荷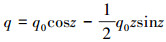


|
| 图 3 悬臂梁结构受力图 |
| 变量 | 分布类型 | 均值 | 标准差 |
| b/cm | 正态分布 | 10 | 0.01 |
| h/cm | 正态分布 | 15 | 0.01 |
| q0/(N·m-1) | 正态分布 | 6 000 | 10 |
| F0/N | 正态分布 | 5 000 | 10 |
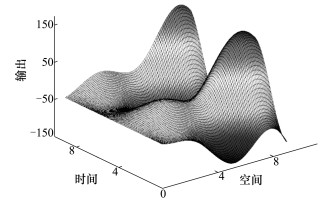
图 4给出了随机输入变量取均值时输出响应σmax随时间和空间位置变化的曲面图, 从图中可以看出, 点(5.22, 0)、(5.22, 6.28) 和(8.18, 3.14) 为输入变量取均值时输出响应的峰值。表 2列出了不同阀值下的失效概率计算结果, 通过与蒙特卡罗方法的结果进行比较, 可以看出该方法计算的准确性。表 3还列出了包络函数法和蒙特卡罗法的计算量, 通过对比可以看出包络函数方法能够很大程度地提高计算效率, 减少计算成本。表 4中的输入变量全局灵敏度计算结果表明, 通过包络函数法得到的输入变量全局灵敏度指标的大小排序与蒙特卡罗法结果相同, 即:h>b>F0>q0, 因此, 通过减少输入变量h的不确定性能够最大程度改善结构的安全性能。
|
| 图 4 均值处输出响应随参数变化图 |
| σ*/MPa | Envelope | MCS |
| 140 | 0.538 91 | 0.537 56 |
| 141 | 0.295 04 | 0.289 21 |
| 142 | 0.140 37 | 0.140 26 |
| 143 | 0.056 50 | 0.055 82 |
| 144 | 0.019 12 | 0.019 21 |
| 145 | 0.005 78 | 0.005 21 |
| 注:Envelope表示本文所提包络函数法 | ||
| σ*/MPa | Envelope | MCS |
| 140 | 482 | 106 |
| 141 | 497 | 106 |
| 142 | 495 | 107 |
| 143 | 480 | 107 |
| 144 | 475 | 107 |
| 145 | 486 | 107 |
| 变量 | Envelope | MCS |
| b | 0.074 6 | 0.084 1 |
| h | 0.095 0 | 0.089 2 |
| q0 | 0.000 2 | 0.000 3 |
| F0 | 0.000 8 | 0.001 3 |
| Ncall | 2 766 | 108 |
| 注:此时为选取σ*=144时的输入变量灵敏度指标。 | ||
对于如下所示的串联多输出系统:
由以上的计算结果可以看出, 所提方法对于多输出问题仍然适用。从表 5可以看出包络函数法计算出的多输出动态可靠性问题的失效概率与蒙特卡罗方法基本相同, 但是却能大大地减少计算量。从表 6可以看出, 使用包络函数法得出的输入变量全局灵敏度指标排序与蒙特卡罗法得出的排序结果相同, 即:x1>x>x3, 因此, 与其它输入变量相比, x1的随机性对失效概率的影响最大, 可以通过减小x1的不确定性来提高系统的安全性。
| 变量 | Envelope | MCS |
| x1 | 0.092 2 | 0.125 6 |
| x2 | 0.050 1 | 0.045 5 |
| x3 | 0.006 1 | 0.010 3 |
| Ncall | 4 968 | 108 |
本文提出了一种计算时间和位置多参数的动态可靠性分析的包络函数方法, 该方法通过使用多个展开点处的分段超平面来近似原随时间和空间连续变化的失效超曲面, 计算精度高而计算量较小。同时, 该方法亦适用于多输出系统。算例结果显示, 所提方法能够将计算量减小4个量级左右, 因此所提方法具有高效性。
鉴于基于失效概率的可靠性全局灵敏度指标在结构安全及可靠性评估领域中的重要作用, 本文提出了基于包络函数法和三点估计法的时空动态可靠性全局灵敏度指标的高效算法。所提方法能够在保证计算精度的同时, 很大程度上减小了计算量, 从而高效地找出影响结构动态安全的重要性变量并为后续的结构优化设计提供指导。
本文方法计算精度与输入变量的变异性及功能函数的非线性程度有关。对于输入变量变异性较大或功能函数的非线性程度较大的情况, 使用该方法可能会得到较大的误差。不过针对该问题, 可以采取一定的手段来提高它的精度, 比如使用更多的展开点等, 这将在后续的工作中进行研究。
| [1] | Zhang J, Wang J, Du X. Time-Dependent Probabilistic Synthesis for Function Generator Mechanisms[J]. Mechanism and Machine Theory, 2011, 46(9): 1236-1250. DOI:10.1016/j.mechmachtheory.2011.04.008 |
| [2] | Thoft-Christensen P, Murotsu Y. Application of Structural Systems Reliability Theory[M]. Berlin: Springer Verlag, 1986. |
| [3] | Ditlevsen O D, Madsen H O. Structural Reliability Methods[M]. New York: Wiley, 1996. |
| [4] | Hohenbichler M, Rackwitz R. Improved of Second-Order Reliability Estimates by Importance Sampling[J]. Journal of Engineering Mechanics, ASCE, 1988, 114(12): 2195-2199. DOI:10.1061/(ASCE)0733-9399(1988)114:12(2195) |
| [5] | Du X, Sudjianto A. The First Order Saddlepoint Approximation for Reliability Analysis[J]. American Institute of Aeronautics and Astronautics Journal, 2015, 42(6): 1199-1207. |
| [6] |
吕震宙, 宋述芳, 李洪双. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.
Lu Zhenzhou, Song Shufang, Li Hongshuang. Reliability and Reliability Sensitivity Analysis of Structural Mechanism[M]. Beijing: Science Press, 2009. (in Chinese) |
| [7] | Li J, Chen J B, Fan W H. The Equivalent Extreme-Value Event and Evaluation of the Structural System Reliability[J]. Structure Safety, 2007, 29(2): 112-131. DOI:10.1016/j.strusafe.2006.03.002 |
| [8] | Chen J B, Li J. The Extreme Value Distribution and Dynamic Reliability Analysis of Nonlinear Structures with Uncertain Parameters[J]. Structure Safety, 2007, 29(2): 77-93. DOI:10.1016/j.strusafe.2006.02.002 |
| [9] | Li J, Mourelators Z P. Time-Dependent Reliability Estimation for Dynamic Problems Using a Niching Genetic Algorithm[J]. Journal of Mechanical Design, 2009, 131(7): 1119-1133. |
| [10] | Sudret B. Analytical Derivation of the Outcrossing Rate in Time-Variant Reliability Problems[J]. Structure & Infrastructure Engineering, 2008, 4(5): 353-362. |
| [11] | Schrupp K, Rackwitz R. Outcrossing Rates of Marked Poisson Cluster Processes in Structural Reliability[J]. Applied Mathematical Modelling, 1988, 12(5): 482-490. DOI:10.1016/0307-904X(88)90085-6 |
| [12] | Rice S O. Mathematical Analysis of Random Noise[J]. Bell System Technical Journal, 1945, 24(3): 46-156. |
| [13] | Bastard G. Superlattice Band Structure in the Envelope Function Approximation[J]. Physical Review B, 1981, 24(24): 5693-5697. |
| [14] | Xia R W, Chen S J. A Quasi-Analytic Method for Structural Optimization[J]. Communications in Numerical Methods in Engineering, 1998, 14(6): 569-580. DOI:10.1002/(SICI)1099-0887(199806)14:6<>1.0.CO;2-9 |
| [15] | Jeong J L, Byung C L. Efficient Evaluation of Probabilistic Constraints Using an Envelope Function[J]. Engineering Optimization, 2005, 37(2): 185-200. DOI:10.1080/03052150512331315505 |
| [16] | Du XP. Time-Dependent Mechanism Reliability Analysis with Envelope Functions and First-Order Approximation[J]. Journal of Mechanical Design, 2014, 136(8): 52-68. |
| [17] | Wei PF, Lu ZZ, Hao WR. Efficient Sampling Methods for Global Reliability Sensitivity Analysis[J]. Computer Physics Communications, 2012, 183(8): 1728-1743. DOI:10.1016/j.cpc.2012.03.014 |
| [18] | Cui LJ, Lu ZZ. Moment-Independent Importance Measure of Basic Random Variable and Its Probability Density Evolution Solution[J]. Science China Technological Sciences, 2010, 53(53): 1138-1145. |
| [19] | Seo HS, Kwak BM. Efficient Statistical Tolerance Analysis for General Distributions Using Three-Point Information[J]. International Journal of Production Research, 2002, 40(40): 931-944. |
| [20] |
张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J]. 航空学报, 2014, 35(8): 2199-2206.
Zhang Leigang, Lu Zhenzhou, Chen Jun. An Efficient Method for Failure Probability-Based Moment-Independent Importance Measure[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2199-2206. (in Chinese) |


