2. 徐州工程学院 数理学院, 江苏 徐州 221018
迭代学习控制[1](iterative learning control, 简称ILC) 是人工智能与自动控制相结合的学习控制技术, 它是一种无模型控制, 不需要具体的模型参数, 只需利用自身重复性的特性, 进行足够多次的学习, 便可使被控对象完全跟踪理想输出。正是由于这一特性, 迭代学习控制自提出以来就受到国内外众多学者的青睐, 涌现出大量的研究成果, 这些成果主要是在整数阶系统下研究的。但现实世界中的动态系统主要是分数阶的, 与整数阶模型相比, 分数阶模型能够更加准确地描述动态系统。因此, 将迭代学习控制应用于分数阶系统逐渐成为一个新的研究热点[2-9]。
2001年, 文献[2]首次提出Dα-型迭代学习控制律, 并得到其在频域中的收敛条件, 推广了迭代学习控制的应用范围。在时域内, 文献[3-5]分别针对分数阶线性系统、非线性系统在理论上严格分析了P-型迭代学习控制律的收敛性, 并获得了所对应的收敛条件。文献[6]针对分数阶线性时不变系统, 给出了PDα-型迭代学习控制律收敛的充分条件。文献[7-8]研究了分数阶非线性系统PDα-型迭代学习控制律的收敛性问题。考虑到反馈控制的优点, 在文献[6]的基础上, 文献[9]将PDα-型迭代学习控制律拓展到更一般的开闭环PDα-型迭代学习控制律, 并给出了控制律收敛的充分条件。
以上研究分数阶迭代学习控制的文献是在λ-范数意义下对跟踪误差进行度量。在某种程度上, λ-范数不能对跟踪误差的本质特征客观地量化描述[10-11]。相关文献[12-13]研究发现, 当选取比较大的参数λ时, 虽然在理论上能保证学习律的单调收敛, 但在系统的重复运行过程中, 它的暂态跟踪误差的上确界值不在实际工程的误差容许范围内, 从而导致系统崩溃。为了使系统的收敛性不依赖参数λ的选取, 而主要取决于系统本身的动力学特性以及学习增益[14], 针对一类分数阶线性时不变系统, 本文选取Lebesgue-p范数作为迭代学习控制收敛性的分析工具, 利用卷积的推广Young不等式对具有反馈信息的PDα-型迭代学习控制律的收敛条件进行了严格的数学证明, 并通过数值算例进行仿真实验。仿真结果对理论的正确性和有效性进行了验证。
1 预备数学知识本节给出文中所需的数学知识。
定义1 对于连续向量函数f:[0, T]→Rn, f(t)=[f1(t), f2(t), …, fn(t)]T, λ为一正实数, 则函数f的λ-范数表示为
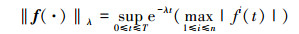
|
函数f的上确界范数和Lebesgue-p范数分别为
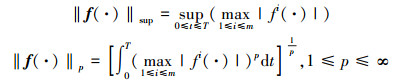
|
特别地, 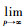
通过上式可以得出, 上确界范数‖f(·)‖sup是Lebesgue-p范数的特例。
定义2 设函数g、h在A⊂R上可积, 对于任意的t∈A, 若积分
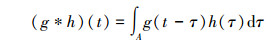
|
都存在, 则称g*h为函数g和h的卷积。
引理1[14] 对于勒贝格可积函数g(t)∈Lq和h(t)∈Lp, t∈[0, T], 其对应的卷积的广义Young不等式为
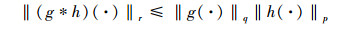
|
1≤p, q, r≤∞, 
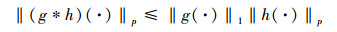
|
定义3[15] (分数阶微积分) 分数阶的统一积分公式定义为
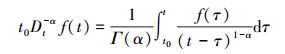
|
式中, f(t) 是任意可积函数, t0Dt-α f(t) 表示f(t) 在区间[t0, t]上的α(α>0) 次分数阶积分, 且Γ(α)=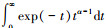
对任意正实数α, Riemann-Liouville和Caputo的分数阶导数分别定义为
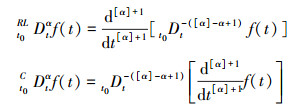
|
式中, [α]表示α的整数部分, RLD和CD分别表示Riemann-Liouville和Caputo的分数阶导数。
定义4[16] 双参数的Mittag-Leffler函数在分数阶微积分中起着十分重要的作用, 其定义为
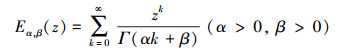
|
特别地, 当β=1时, 单参数的Mittag-Leffler函数的定义为
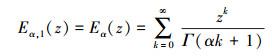
|
引理2[17] 初值问题
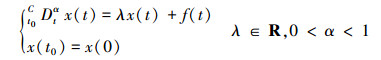
|
的解为
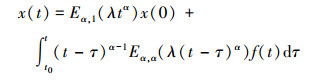
|
对于分数阶线性时不变系统
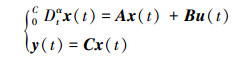
|
(1) |
式中, t∈[0, T], α∈(0, 1), (·)α表示α阶Caputo导数, 初始状态为x(0), 状态向量x(t)、系统的控制输入u(t) 和系统输出y(t) 分别是n×1、p×1和m×1的列向量, A、B、C分别是n×n、n×p和m×n的常数矩阵。
为了证明方便, 给出文中算法的合理假设:
假设1 系统 (1) 在区间[0, T]上多次重复运行时的初始状态可重置, 且给定区间[0, T]上可微的理想输出yd(t)(t∈[0, T]), 存在唯一理想控制输入ud(t), 使得系统的状态和输出为理想值xd(t) 和yd(t)。
假设2 CB为满秩矩阵。
设u1(t)(t∈[0, T]) 为一任意值, 为初次输入的控制输入。在上一次的跟踪误差和跟踪误差的α阶导数的基础上, 考虑其当前次跟踪误差及跟踪误差的α阶导数来修正当前次的控制输入, 即具有反馈信息的PDα-型迭代控制律, 其表达式如下
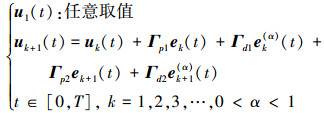
|
(2) |
式中, Γp1和Γd1分别为比例和微分学习增益矩阵, Γp2和Γd2分别为比例和微分反馈增益矩阵; ek(t)=yd(t)-yk(t) 表示第k次迭代系统的跟踪误差, yk(t) 表示第k次迭代的系统输出。
当Γp2=Γd2=0时, 控制律 (2) 退化为典型的PDα-型控制律, 其表达式如下
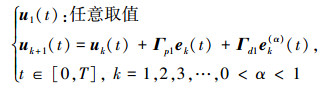
|
(3) |
当系统 (1) 中的控制输入由控制律 (2) 替换时, 对应的系统变为
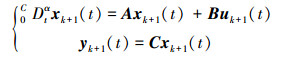
|
(4) |
定理 设分数阶系统 (1) 满足假设1、2, 当控制律 (2) 作用于系统 (1) 时, 如果学习增益矩阵Γp1、Γd1和反馈增益矩阵Γp2、Γd2以及系统矩阵A、B、C满足下列条件:
1) ρ2>0,
2) ρ2ρ1 < 1,
式中
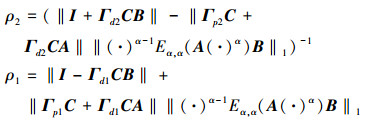
|
则在Lebesgue-p范数意义下, 当迭代次数k→∞时, 跟踪误差单调趋向于零, 即
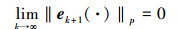
|
且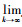
证明 设
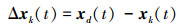
|
(5) |
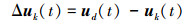
|
(6) |
由 (4) 式可得
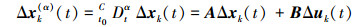
|
(7) |
因此
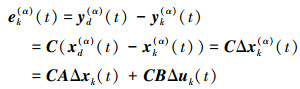
|
(8) |
由 (2) 式可得
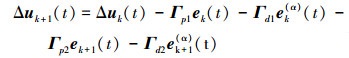
|
(9) |
将 (8) 式代入 (9) 式, 整理得
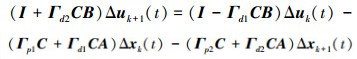
|
(10) |
对 (10) 式两边同时取Lebesgue-p范数, 可得
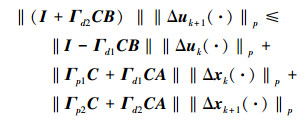
|
(11) |
根据引理2, 由 (4) 式可得
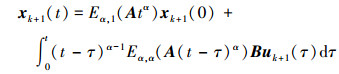
|
(12) |
根据假设1, 可得
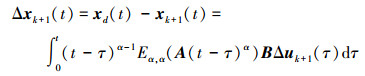
|
(13) |
对 (13) 式两边同时取Lebesgue-p范数, 并运用卷积的推广Young不等式, 可得
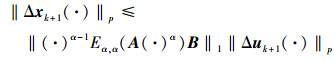
|
(14) |
同理, 可得
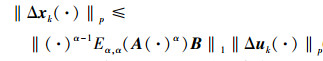
|
(15) |
将 (14)、(15) 式代入 (11) 式, 并由条件1)、2), 整理得
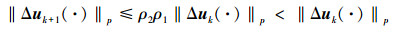
|
(16) |
所以
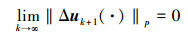
|
由 (13) 式, 可得
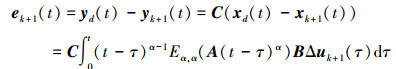
|
(17) |
对 (17) 式两边同时取Lebesgue-p范数, 并运用卷积的推广Young不等式, 可得
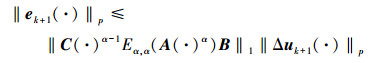
|
(18) |
又因为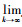
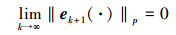
|
(19) |
这说明, 在Lebesgue-p范数意义下, 当迭代次数k→∞时, 跟踪误差单调趋向于零。
所以
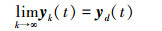
|
当Γp2=Γd2=0时, 控制律 (2) 退化为典型的PDα-型控制律 (3), 当控制律 (3) 作用于分数阶系统 (1) 时, 可得到如下结论:
推论 设分数阶系统 (1) 满足假设1、2, 当控制律 (3) 作用于系统 (1) 时, 如果学习增益矩阵Γp1、Γd1以及系统矩阵A、B、C满足下列条件:
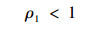
|
式中
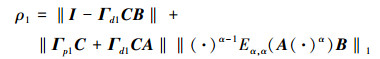
|
则在Lebesgue-p范数意义下, 当迭代次数k→∞时, 跟踪误差单调趋向于零, 即
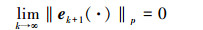
|
且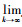
注1 从控制律 (2) 的收敛条件可知, 在Lebesgue-p范数意义下, 控制律的收敛性不仅取决于控制律的学习增益, 而且依赖于系统本身的属性。
注2 相对于文献[9]中λ-范数意义下的收敛条件ρ*=(‖I+Γd2CB‖)-1‖I-Γd1CB‖ < 1, 本文提出的控制律的收敛条件比较保守, 但控制律的收敛性分析和误差度量不依赖参数λ的取值。
注3 从收敛性分析中可知, ρ2ρ1的大小决定了控制律 (2) 收敛速度的快慢, 即ρ2ρ1的值越小, 控制律 (2) 的收敛速度越快。由定理和推论的收敛条件可知, 当ρ1 < 1且ρ2 < 1时, 有ρ2ρ1 < ρ1 < 1, 这表明, 控制律 (2) 拥有比控制律 (3) 更快的收敛速度。
3 数值仿真考虑如下分数阶线性时不变系统
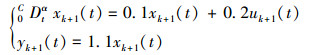
|
式中, 系统的运行区间为[0,1]。
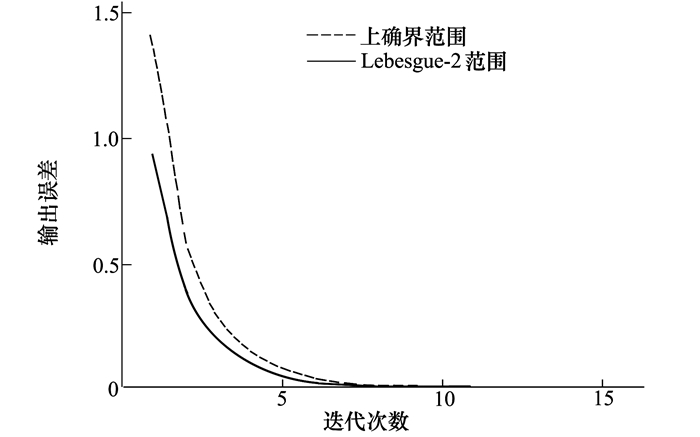
给定理想输出yd(t)=12t2(1-t), 初始控制输入u1(t)=0, t∈[0,1]。在迭代学习控制律 (2) 中选取α=0.9, Γp1=0.9, Γd1=1.9, Γp2=0.3, Γd2=1。可以算出ρ1=0.7836 < 1, ρ2=0.8945 < 1, 且ρ2ρ1 < ρ1 < 1, 满足定理的收敛条件。图 1所示为控制律 (2) 作用于分数阶系统时跟踪误差的变化趋势, 可以看出, 在Lebesgue-2范数和上确界范数的意义下, 随着迭代次数的增加, 两者跟踪误差都单调趋向于零。
|
| 图 1 控制律 (2) 的跟踪误差变化趋势 |
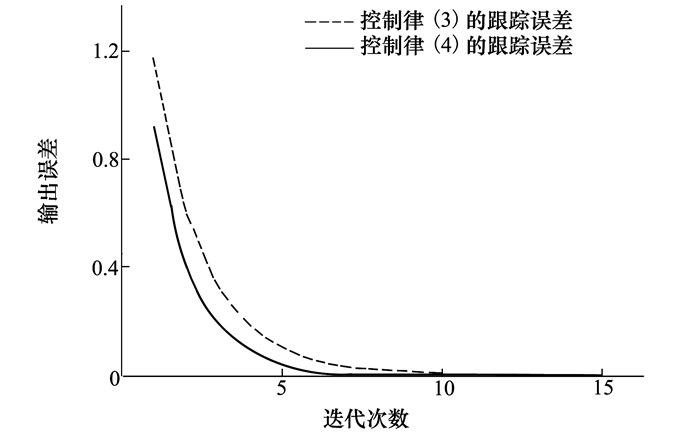
在上述条件下, 控制律 (2)、(3) 分别作用于分数阶系统时跟踪误差如图 2所示。从图中的误差曲线可以看出, 在Lebesgue-2范数的意义下, 控制律 (2)、(3) 的跟踪误差随着迭代次数增加, 两者都单调趋向于零; 且ρ2ρ1 < ρ1 < 1时, 控制律 (2) 迭代7次便可达到误差范围 (0.0077), 而典型的PDα-型控制律 (3) 需要10次迭代才能达到上述效果, 即控制律 (2) 拥有比控制律 (3) 更快的收敛速度, 同理论结果相符。
|
| 图 2 控制律 (2)、(3) 的跟踪误差比较 |
针对一类分数阶线性时不变系统, 本文选取Lebesgue-p范数作为迭代学习控制收敛性的分析工具, 利用卷积的推广Young不等式对具有反馈信息的PDα-型分数阶迭代学习控制律单调收敛性进行了严格理论分析, 并获得其单调收敛的充分条件。仿真结果表明, 相比典型的PDα-型控制律, 选取适当的反馈增益后, 具有反馈信息的PDα-型分数阶迭代学习控制律拥有更快的收敛速度。基于本文的研究方法, 可推广到研究分数阶非线性系统的收敛性及收敛速度等。
| [1] | Arimoto S, Kawamura S, Miyazaki F. Bettering Operation of Robotics by Learning[J]. Journal of Robotic System, 1984, 12(2): 123–140. |
| [2] | Chen Y Q, Moore K L. On Dα-Type Iterative Learning Control[C]//Proceedings of IEEE Conference on Decision and Control, 2001:4451-4456 |
| [3] |
兰永红, 刘潇.
分数阶线性系统二阶P型迭代学习控制收敛性分析[J]. 控制工程, 2016, 23 (3): 341–345.
Lan Yonghong, Liu Xiao. Convergence Analysis of Second-Order P-Type Iterative Learning Control of Fractional Order Linear Systems[J]. Control Engineering of China, 2016, 23(3): 341–345. (in Chinese) |
| [4] | Li Y, Ahn H S, Chen Y Q. Iterative Learning Control of a Class of Fractional Order Nonlinear Systems[C]//Proceedings of the IEEE International Symposium on Intelligent Control, Part of IEEE Multi-Conference on Systems and Control, 2010:779-782 |
| [5] | Lan Y H. Iterative Learning Control with Initial State Learning for Fractional Order Nonlinear Systems[J]. Computers and Mathematics with Applications, 2012, 64: 3210–3216. DOI:10.1016/j.camwa.2012.03.086 |
| [6] | Lazarevic M P. PDα——Type Iterative Learning Control for Fractional LTI System[C]//Proceedings of the 16th International Congress of Chemical and Process Engineering, Prague, Czech Republic. 2004:271-275 |
| [7] | Li Y, Chen Y Q, Ahn H S. On the PDα-Type Iterative Learning Control for the Fractional-Order nonlinear Systems[C]//Proceedings of the American Control Conference, 2011:4320-4325 |
| [8] | Lazarevic M P. Iterative Learning Feedback Control for Nonlinear Fractional Order System PDα-Type[C]//Proceedings of the 4th IFAC Workshop Fractional Differentiation and Its Applications, 2012:259-265 |
| [9] | Lazarevic M P, Mandic P. Feedback-Feedforward Iterative Learning Control for Fractional Order Uncertain Time Delay System PDα-Type[C]//International Conference on Fractional Differentiation and Its Applications, 2014:1-6 |
| [10] | Xu J X, Hou Z S. A Survey of Iterative Learning Control:A Learning-Based Method for High-Performance Tracking Control[J]. Acta Automatica Sinica, 2005, 31(6): 943–955. |
| [11] | Andres D, Pandit M. Convergence and Robustness of Iterative Learning Control for Strongly Positive Systems[J]. Asian Journal of Control, 2002, 4(1): 1–10. |
| [12] | Lee H S, Bien Z. A Note on Convergence Property of Iterative Learning Controller with Respect to Sup-Norm[J]. Automatica, 1997, 33(8): 1591–1593. DOI:10.1016/S0005-1098(97)00068-X |
| [13] | Park K H, Bien Z. A Study on Iterative Learning Control with Adjustment of Learning Interval for Monotone Convergence in the Sense of Sup-Norm[J]. Asian Journal of Control, 2002, 4(1): 111–118. |
| [14] |
阮小娥, 连建帮, 吴慧卓.
具有反馈信息的迭代学习控制律在Lebesgue-p范数意义下的收敛性[J]. 自动化学报, 2011, 37 (4): 513–516.
Ruan Xiaoe, Lian Jianbang, Wu Huizhuo. Convergence of Iterative Learning Control with Feedback Information in the Sense of Lebesgue-p Norm[J]. Acta Automatica Sinica, 2011, 37(4): 513–516. (in Chinese) |
| [15] | Podlubny I. Fractional Differential Equations[M]. San Diego, Academic Press: , 1999. |
| [16] | Agarwal R P. A Propos D'une Note de M. Pierre Humbert[J]. CR Acad Sci Paris, 1953, 236(21): 2031–2032. |
| [17] | Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations[M]. New York, Elsevier: , 2006. |
2. School of Math and Physical Sciences, Xuzhou Institute of Technology, Xuzhou 221018


