2. 西北工业大学 计算机学院, 陕西 西安 710072
近十年以来,计算成像学在计算机视觉和计算机图像学领域得到广泛关注。不同于传统成像技术,计算成像技术提升和扩展了数字成像能力,比如动态范围、聚焦控制、快门速度、景深范围、光学孔径等。 基于光场理论的虚拟孔径成像是计算成像学的一个典型应用[1-2]。相机阵列虚拟孔径成像以多台相机模拟1台大孔径相机的成像效果,其优势在于具有先拍照后对焦,灵活控制景深的成像特性。也就是说,虚拟孔径成像技术通过后处理算法能够合成1幅聚焦在指定平面或曲面的图像,甚至可实现逐像素精度对焦。相机阵列排布结构所导致数据采集的离散特性,使得其后期合成图像中存在鬼影问题,即散焦区域出现多块相同的边缘和特征。鬼影问题是虚拟孔径成像技术获取高质量图像的瓶颈,因此鬼影的去除成为提高虚拟孔径成像质量的热点问题。目前,大多数方法均采用多视角图像估计深度信息,然后计算每个像素的但扩散函数,最后依据相应的扩散模拟算法减轻图像的鬼影问题。由于遮挡、噪声以及复杂纹理等问题的影响,基于图像的深度估计方法仍存在精度不足和可靠性低的问题。因此,现有虚拟孔径成像去鬼影方法实用过程中仍面临需高精度深度先验信息的瓶颈。
为提高虚拟孔径图像质量,本文提出一种场景深度无关的鬼影去除方法。本文通过分析相机阵列参数和光场采样之间的关系来阐明鬼影产生原因。随后,该方法根据基于熵值计算结果逐像素预测低通滤波核函数的半径。最终,该方法采用基于相邻像素和相邻深度对低通滤波器进行优化,并采用逐像素滤波减弱了散焦区域的鬼影现象。
1 相关工作一般情况下,任何成像过程都可视为对1个7维全光函数的降采样过程。假设光线在空间沿1条直线自由传播,并忽略波长和时间维度,1条光线通过其所经过的2个平行平面可被唯一确定,该模型常被称为光场的双平面参数化表示[1]。对于给定场景深度为d的平面, 可通过(1)式聚焦合成在该平面上的图像
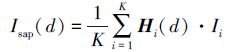
|
(1) |
式中, Hi(d)表示光线从原始聚焦深度到深度d的传播矩阵, Ii表示K个不同角度采样中的第i视角图像。由于相机阵列只能获取角度-空间降采样的光场信号, 因此其散焦区域会出现本文所关注的鬼影现象。
为了消除鬼影效应, Levoy 等人[1]提出一种有效的预滤波方法, 但该方法的预滤波过程降低了图像聚焦区域的清晰度。Gorler等人[3]提出了逐像素低通滤波的方法减弱鬼影效应, 但该方法需要高精度深度先验信息, 其应用场合受到了一定的限制。Chai 等人[4]提出一种光场重采样方法, 该方法计算得到了光场最小采样率曲线, 该方法首次引入了光场渲染和传统几何渲染的关系。为提升图像分辨率并去除鬼影效应, Georgiev 等人[5]讨论了传感器-微透镜结构对光场采样的影响, 并分析了光场角度与空间采样的折衷关系。
由于很难获取精确的场景深度, 研究者们提出了一些无需精确估计深度的欠采样光场图像渲染方法以改善鬼影效应。Bishop等人[6]提出一种光场动态重参数化方法, 能够在指定深度渲染降低鬼影效应, 其限定了场景视差应在一个像素以内。Stewart 等人[7]通过提出一种空间双遍滤波方法解决图像鬼影问题, 但频域重建过程要求相机阵列孔径的基线足够大, 这一要求在实际中很难达到。Ng提出了基于傅里叶切片定理的频域滤波方法生成虚拟孔径图像, 他指出不同深度的聚焦图像对应于4D光场在频域中不同角度的切片, 但高频区域的混叠使得鬼影现象难以避免[8]。Levin 等人[9]通过分析了光场采样过程角度-空间采样的折衷问题, 提出基于贝叶斯框架的高斯混合先验可用于降低虚拟孔径图像的鬼影效应, 但其高斯混合先验仍需对场景深度信息进行估计。
2 虚拟孔径成像的鬼影去除算法如(1)式所示, 虚拟孔径成像的每个像素值由K个源像素点积分而成。若一个3D点p位于虚拟孔径的焦平面, 从光源发出的光线经p点反射, 在成像平面聚集于一点px;若p点偏离焦平面, 从p点发出的反射光线聚集于一块圆形区域。该圆形区域称为弥散圆[10], 其半径为
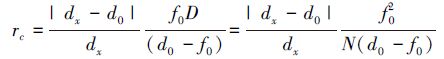
|
(2) |
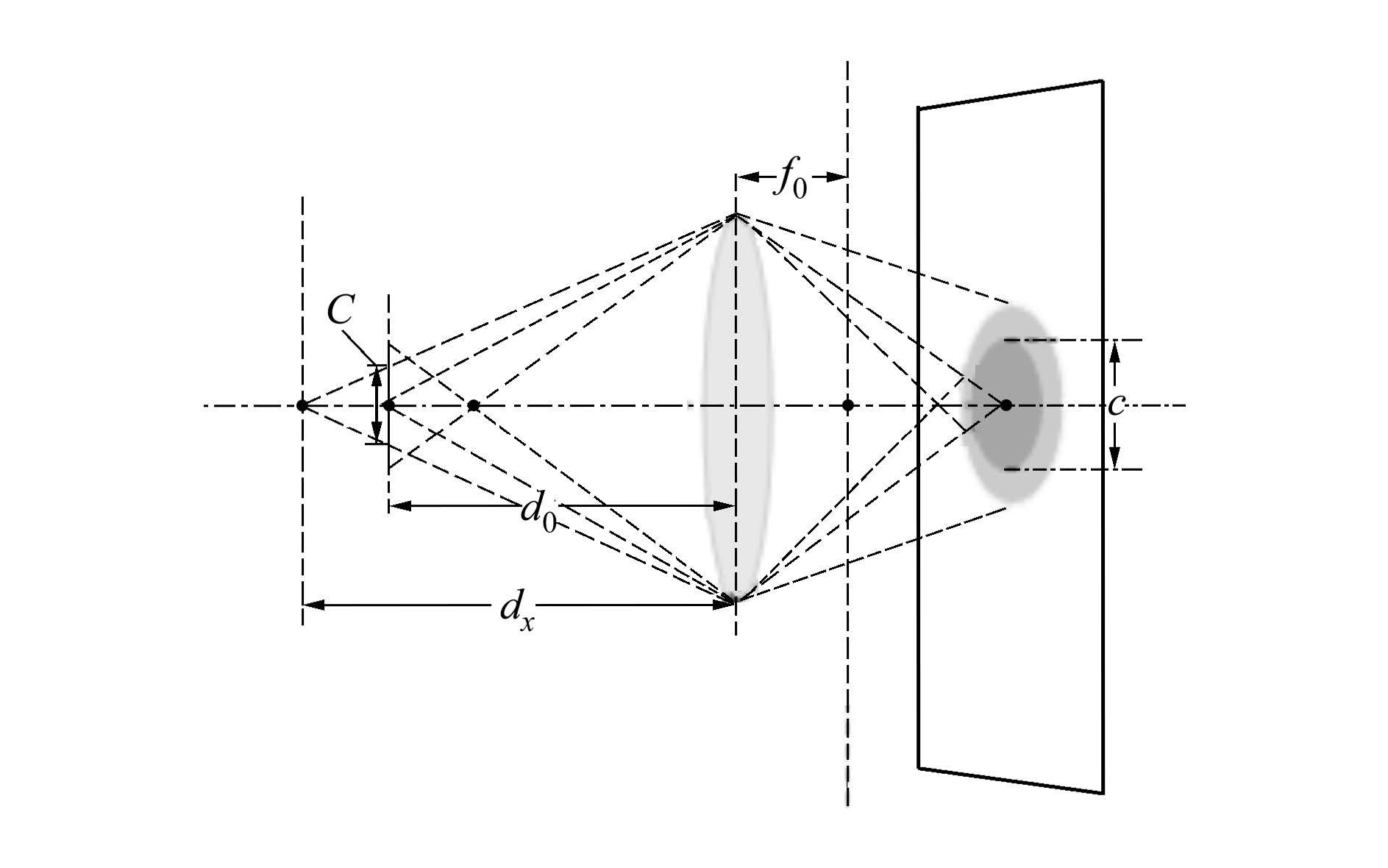
式中, f0表示焦距, d0表示焦平面深度, D表示透镜直径。由于虚拟孔径图像单个像素由K个源像素点合成, 因此弥散圆ΩC的半径表示为rC=mrc, 其中m=(d0-f0)/f0。
对于图像I中每个像素点px, 其颜色值为
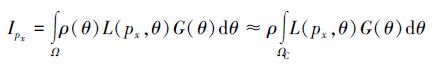
|
(3) |
式中, L(px, θ)表示位置为px, 角度为θ的采样光线, θ表示光线和成像平面法向量的夹角, G(θ)表示光线l(px, θ)在角度θ上的权重函数, ρ(θ)表示传感器角度灵敏度。为简化模型, 使ρ(θ)为常数ρ。
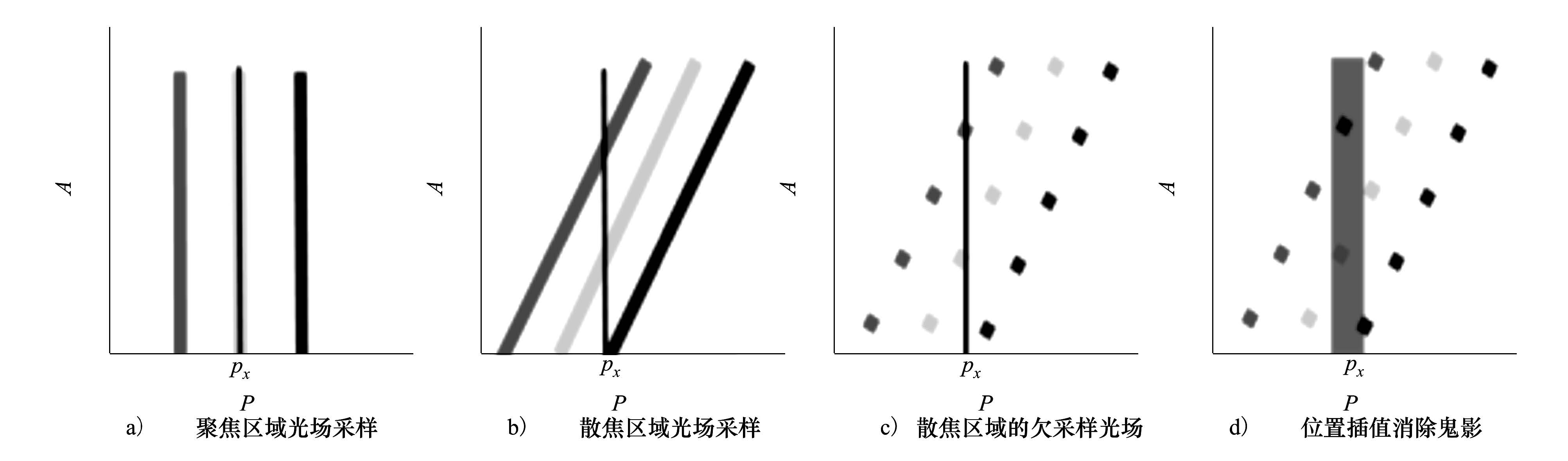
为了叙述的方便起见且不失一般性, 我们在简化的二维光场模型中对本文鬼影去除算法的思想进行说明, 该二维光场模型能够容易的扩展至四维光场模型中。假设焦平面上有3个不同颜色值的朗伯点, P表示光线位置坐标, A表示光线角度, 将2D光场表示在笛卡尔坐标系中, 如图 3a)所示。相同位置的光场采样具有不变性, 也就是说, 不同角度方向的光线采样来自于同一个三维空间点。在这种情况下, 空间点发出的光线完全聚焦于成像平面, 因此不存在模糊。假如将焦平面偏离该聚焦平面进行前后移动, 其二维光场表示则如图 3b)所示。此时, 相机阵列仅能捕获同一空间点发出的有限角度光线。
|
| 图 1 目标场景和成像区域中的弥散圆示意 |
由于光场在角度方向上采样不足, 即光场存在欠采样问题, 则其虚拟孔径成像结果中出现鬼影。图 3a)~图 3b)中的黑色竖直线表示在px点的采样。如图 3b)所示, 3条斜线表示采样光场, px点的采样与这3条线相交, 因此px点是这3种颜色值的积分。但在欠采样光场中不同, 如图 3c)所示, 成像平面在px点仅能记录图中2种灰度的采样值, 该情况下会出现鬼影。为解决这一问题, 已有方法是在角度采样上插值或在角度坐标轴上使用滤波器[12]。但在角度维采样密度非常低的情况下, 这些方法仍然不能达到令人满意的效果。
|
| 图 3 2D光场采样示意图 |
本文算法利用相邻位置信息恢复原始光场信号。如图 3d)所示, 在px位置选择一个宽度合适的窗口, 那么所有不同颜色值的采样都包含在新的灰色竖线窗口中, 则其积分成像结果将不存在鬼影效应。也就是说, 光场位置维度上的低通滤波器能够弥补角度采样率上的不足。新的积分函数可表示为
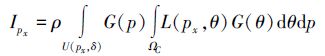
|
(4) |
式中, U(px, δ)表示点px的邻域, δ表示空域低通滤波器半径, G(p)表示和光线位置相关的权重函数。px点成像结果的计算过程不仅涉及该位置的多个角度采样, 还包括其邻域位置的角度采样点。参数δ随着空间点和焦平面之间距离的变化而改变。若px偏离焦平面, 由(2)式计算所得的rC、δ值随着rC增大而增大。由于深度未知的假设, δ无法由(2)式直接计算得到。因此本文提出一个基于熵值的自适应计算δ的方法。该算法基于以下3个假设。
假设1 角度采样的熵值正相关于弥散圆大小。
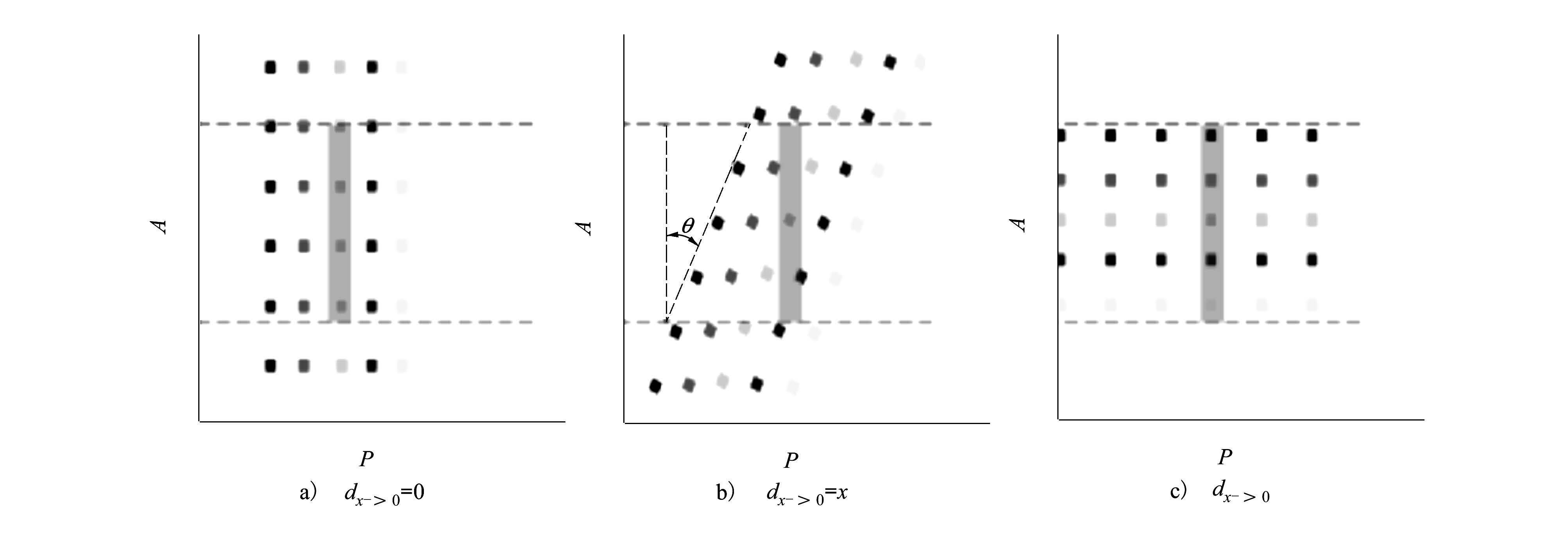
如图 4所示, 在2D光场中, 采样点的斜率tanθ由物点和焦平面之间的距离dx→0=dx-d0计算得到, 且成正相关, 即dx→0∝tanθ。图 4中的灰色矩形框宽度表示一个采样宽度。随着tanθ的增加, 理论上角度采样的熵值响应增加。基于这一假设, 根据角度采样的熵值决定(4)式中δ的值。因此, 对于一个给定光线位置, 熵值越大, 说明弥散圆半径越大, 即
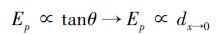
|
(5) |
|
| 图 4 虚拟孔径图像给定像素上采样光场的熵值 |
假设2 聚焦点上角度采样的熵值小于散焦点角度采样的熵值。
如图 4a)所示, 聚焦点上角度采样具有不变性, 理想情况下角度采样的熵值为0。但实际情况中聚焦区域会受到一个具有很小半径δ的低通滤波器影响而变得模糊。不考虑这一模糊的影响, 本文使聚焦区域的熵值为0。
假设3 当焦平面平移固定距离时, 相邻像素点具有相似的熵值。
如果2个点在空间域距离足够小, 那么这2点处于相近场景深度的概率较大。这一假设可作为平滑项, 去除外点。如图 4b)所示, 相同深度平面上物点的2D光场采样分布具有相同的斜率。若观测一个固定角度范围的光场采样, 则相邻像素点的采样斜率相近。因此, 本文使用局部特征U(px, δ)提升熵值计算的鲁棒性。
基于上述3点假设, 本文提出的空域鬼影去除算法流程如下。
步骤1 根据(1)式生成虚拟孔径图像。
步骤2 基于假设1估计光场角度采样的熵值。使E(p(x, y), d0)表示虚拟孔径图像在点p(x, y)的熵值, d0表示焦深。首先, 采用(6)式将光辐射函数归一化到统一颜色空间
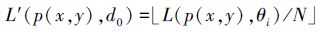
|
(6) |
式中, N表示投射于同一像素点的光线数目。依据公式(7)初始化熵值图
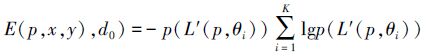
|
(7) |
步骤3 依据相邻聚焦深度图像的聚焦趋势平滑熵值图。根据假设2, 令熵值为E(p(x, y), d0)
步骤4 初始化每个像素点的低通滤波器半径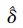
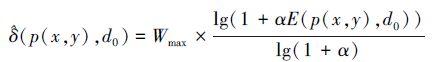
|
(8) |
式中,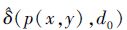
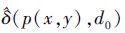

|
(9) |
式中,G(p, σ)表示高斯权重函数, N表示窗口大小, σ=(N/2-1)×0.3+0.8。
步骤5 最终, 对每个像素点进行半径为δ(p(x, y), d0)低通滤波以去除鬼影
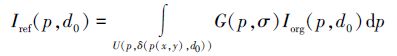
|
(10) |
式中, σ=(δ(p(x, y), d0)/2-1)×0.3+0.8。Iorg(p, d0)和Iref(p, d0)分别表示虚拟孔径原始图像和鬼影去除后的虚拟孔径图像。
3 实验和讨论本文分别在仿真和真实数据上验证了所提出的鬼影去除方法。如图 5和图 6所示, 物点离焦平面越远, 鬼影现象越明显, 采用本文方法后原始虚拟孔径图像上的鬼影被有效减弱。本文设置参数N=25, 将灰度空间中像素灰度值从(0, 255)归一化为(0, 25)。本文选择Tf=0.1, 阈值Tf控制聚焦区域的选择, Tf过小会导致聚焦区域被模糊, 过大则会导致鬼影区域的选取精度降低, 无法有效去除图像中所有鬼影。为了防止过模糊, 使滤波器半径上限Wmax为7个像素宽度, α为10.0。

|
| 图 5 仿真数据的鬼影去除结果 |

|
| 图 6 真实数据的鬼影去除结果 |
对于仿真数据, 首先使用OpenGL建立一个虚拟场景, 通过64个视点获得64幅子图像。因此, 虚拟场景下的实验能够精确控制光辐射度、相机参数以及场景几何关系等参数, 其实验结果如图 5所示。可以看出, 经过本文算法优化, 校正后的δ图优于原始δ图。鬼影效应得到较好降低, 聚焦区域的清晰度和原始虚拟孔径图像保持一致。上面行的聚焦点在右边书本上, 因此最左边书上出现明显鬼影效果。下面行的聚焦点在最左边书上, 因此鬼影出现在右边书上。在椭圆形圆圈指出的图中, 原始虚拟孔径图像具有明显鬼影, 但在应用本文提出算法后的结果中, 鬼影被极大消除。
对于真实数据, 采用8×8相机阵列以30 frame/s的帧率同时捕获64幅不同视角的图像, 并采用(1)式生成在不同焦平面上的虚拟孔径图像序列。如图 6所示, 本文在真实数据进行2组实验, 2组实验均在前景聚焦和背景聚焦2种情况下应用本文算法。通过在每个像素上使用低通滤波器, 散焦区域的鬼影得以去除, 且聚焦区域仍然清晰。这验证了本文所提出方法在无需深度估计条件下仍可有效去除虚拟孔径成像的鬼影效应。
虽然上述实验在仿真和真实数据上均证明了算法有效性, 但本文方法仍存在以下不足之处:首先, 本文实验中一些参数需凭经验设置, 限制了算法的灵活性。其次, 本文算法尚未考虑遮挡, 若聚焦区域被前景遮挡, 鬼影去除后聚焦区域将被模糊, 不能再清晰聚焦。
4 结论本文基于2D光场理论分析了虚拟孔径图像中鬼影效应的产生原因。为在不进行深度估计的条件下有效去除图像鬼影, 本文提出了熵值计算假设以预测图像点聚焦趋势, 从而实现在空域采用低通滤波方法去除图像鬼影。其中, 滤波器核半径通过分析邻域像素和相邻聚焦图像之间关系计算得到。在仿真数据和真实数据上的实验均验证了本文方法的有效性。本文算法有效降低了虚拟孔径图像散焦区域的鬼影现象, 因而该方法能够进一步用于光场渲染及深度估计等相关应用。
| [1] | Levoy M, Hanrahan P. Light Field Rendering[C]//ACM Siggraph, 1996:31-42 |
| [2] | Vaish V. Synthetic Aperture Imaging Using Dense Camera Arrays[D]. Stanford University, CA, USA, 2007 |
| [3] | Gortler S, Grzeszczuk R, Szeliski R, Cohen F M. The Lumigraph[C]//ACM Siggraph, 1996:43-54 |
| [4] | Chai J X, Tong X, Chan S C, Shum H Y. Plenoptic Sampling[C]//ACM Siggraph, 2000:307-318 |
| [5] | Georgiev T, Lumsdaine A. Depth of Field in Plenoptic Cameras[C]//Proc of Eurographics, 2009 |
| [6] | Bishop T E, Favaro P. The Light Field Camera:Extended Depth of Field Aliasing, and Super-Resolution[J]. IEEE TPAMI, 2011, 34(5): 972–986. |
| [7] | Stewart J, Yu J, Gortler S J, McMillan L. A New Reconstruction Filter for Undersampled Light Fields[C]//Proc of Eurographics Workshop on Rendering, 2003:150-156 |
| [8] | Ng R. Fourier Slice Photography[C]//ACM Siggraph, 2005:735-744 |
| [9] | Levin A, Freeman W T, Durand F. Understanding Camera Trade-Offs through a Bayesian Analysis of Light Field Projections[C]//Proc of ECCV, 2008:88-101 |
| [10] | Hecht E. Optics[M]. 4th ed. San Francisco: Addison Wesley Press, 2001. |
| [11] | Liang C K, Shih Y C, Chen H H. Light Field Analysis for Modeling Image Formation[J]. IEEE Trans on Image Processing, 2011, 20(2): 446–460. DOI:10.1109/TIP.2010.2063036 |
| [12] | Lumsdaine A, Georgiev T. Full Resolution Lightfield Rendering[R]. Adobe Technical Report, 2008 |
2. School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China


