2. 长安大学 电控学院, 陕西 西安 710064
扩频体制下, 卫星信号的同步包括两部分:捕获和跟踪。捕获为跟踪提供伪码相位和载波频率的粗略信息, 使接收到的信号与本地码相差小于跟踪环路的牵引范围, 以辅助跟踪环节完成信号的同步以及解扩解调。根据伪码良好的自相关和互相关特性, 借助相关运算可实现伪码相位的估计, 采用频率扫描或者FFT运算完成多普勒频移的估计。捕获作为复现信号的前提, 其捕获精度直接影响载波和码相位的跟踪性能[1]。
基于FFT的并行频率估计以其易于实现、速度快、精度高等特点引起广泛关注。捕获是一个在时间和频率的二维搜索过程, 在实际工程应用中, 可以采用基于FFT的多通道捕获算法[2]。在时域上利用多通道实现码相位的并行搜索, 频域上使用FFT实现多普勒频率的并行搜索, 可大大提高搜索速率, 实现相位和频率的快速捕获。
基于FFT的频率估计特别适合于实时信号处理, 但FFT运算点数有限, 需要对数据进行截断处理, 引起频谱泄漏。由于栅栏效应, 直接利用FFT进行频率估计, 会带来较大的测量误差, 误差范围为±Δf/2。当载波多普勒频移不等于Δf的整数倍时, 信号的真实频差谱线位于FFT幅值最大的2根谱线之间, 若仍采用最大幅度谱线对应的频率进行估计, 则会出现较大的估计误差。工程应用时, 通常采用插值的方法, 借助最大和次大幅度谱线对应的频率和幅值, 对实际频率进行估计, 可以有效降低频偏的估计误差, 提高捕获精度。
1 频率捕获精度改善算法研究 1.1 Rife算法Rife算法是一种基于FFT的经典频率估计插值算法, 经FFT变换之后, 通过分析其频谱图上最大谱线和相邻2根谱线之间的关系, 然后进行插值, 从而提高频率估计精度[3]。
Rife算法的理论精度分析[4]及计算机模拟的结果表明, 在适度的信噪比条件下, Rife算法的估计范围较宽, 当实际频率位于2个离散频率的中心时, 即信号频率与FFT幅度最大值位置的相对偏差|δ|较大, Rife算法的性能很好, 因此插值不会出现方向错误。而当信噪比较低或者相对偏差|δ|较小时, 估计频率可能位于FFT频谱最大值另一侧 (相对幅值次大处), 从而造成频率插值方向相反, 引起较大的频率估计误差[5], 即当信号的实际频率为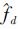
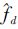
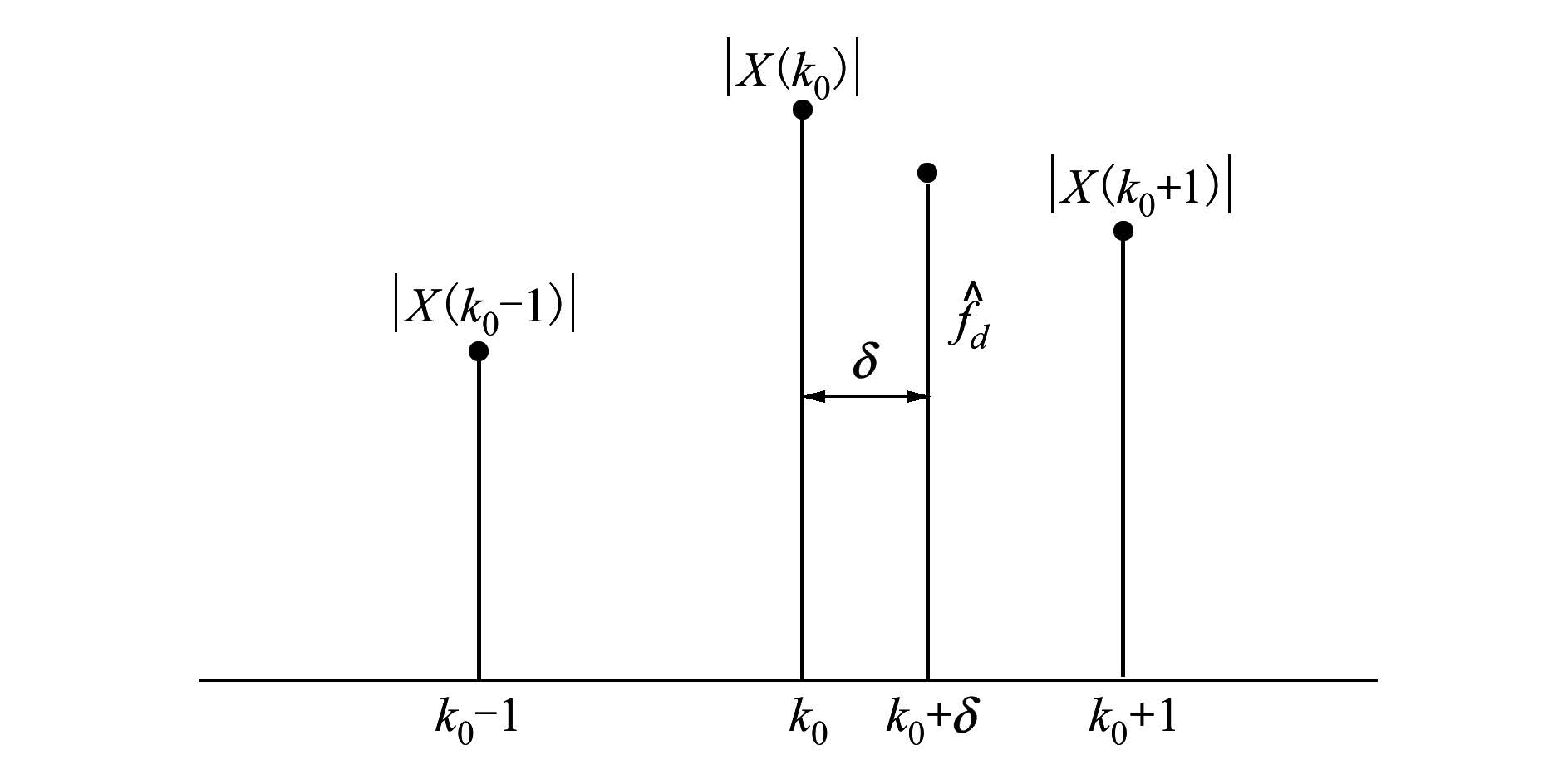
|
| 图 1 Rife算法示意图 |
Quinn算法利用FFT主瓣内的次大谱线与最大谱线系数复数值之比的实部进行频率插值的方法求出相对偏差δ。由于Quinn算法利用了相位信息来判断插值的方向, 不容易出现插值方向错误, 从而避免了在|δ|较小时因插值方向的错误导致频率估计误差激增的问题[6]。
1.3 幅相联合内插算法翟盛华学者提出了一种幅度相位结合的内插算法[7], 该算法充分利用峰值及其左右谱线的幅度信息与相位信息进行综合估计。理论分析证明其是无偏估计, 仿真结果可知, 幅度相位联合内插算法在|δ|较小时保持较高的性能, 且在整个频率范围内接近修正的克拉美罗界, 但这种算法在|δ|较大时性能有所下降。
1.4 改进的捕获精度算法 1.4.1 Q-Rife算法由1.1节和1.2节分析可知, Rife算法在低信噪比小δ下, 容易获得错误的插值方向, Quinn算法虽然可获得正确的插值方向, 但对δ的估算存在很大的风险。针对这2种算法的不足, 本节将提出一种改进的频率内插算法——Q-Rife算法。该算法通过融合利用Rife算法和Quinn算法的优点, 实现更优的频率估计。基于Q-Rife算法的描述, 改进的频率估计值的计算步骤如下:
Step1 根据Rife算法[2]计算相对偏差δ
设接收信号的采样为:x (n)=s (n)+w (n), 其中, s (n)为有用信号, w (n)为混入信号中的加性高斯白噪声, 均值为0, 方差为σ2。设s (n)=aej(2πfc/fs+φ0), 其中a为信号幅度, fc为接收信号频率, fs为信号采样频率, φ0为信号初始相位。
1) 将信号采样x (n) 做N点FFT变换得到X(k), k=1, 2, …, N, 记|X(k)|最大幅度值处的离散频率索引值为k0, 记A0=|X(k0)|, 且k0=round (fc/Δf), 为最接近 (fc/Δf) 的整数。
2) 对应的频率相对偏差为δ, 则δ=fc/Δf-k0且|δ|≤0.5。若δ≠0, 记|X(k)|次大值对应的离散频率索引值为k1, A1=|X(k1)|则k1=k0+1或k1=k0-1。A1和A0的比可表示为:
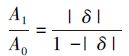
|
(1) |
由 (1) 式可求得|δ|为:
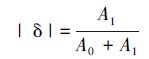
|
(2) |
Step2 根据Quinn算法计算插值的方向r
1) 记录FFT最大谱线及其两侧相邻2根谱线的坐标 (k0, X(k0)), (k0-1, X(k0-1)), (k0+1, X(k0+1)), 计算α1=Re (X(k0-1)/X(k0)), α2=Re (X(k0+1)/X(k0)), 其中Re (x), 表示取x的实部[4]。
2) 由α1和α2分别计算偏差δ1=α1/(1-α1), δ2=α2/(1-α2)。根据δ1和δ2的符号判断频率偏差δ的取值:若δ1, δ2均大于0, r=1, 否则r=-1。
Step3 计算确定的相对偏差δ′
结合Rife算法计算的相对偏差δ和Quinn算法求出的插值方向, 得到最终确定的相对偏差δ′=r×|δ|。
Step4 计算频率估计值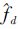
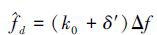
|
(3) |
Q-Rife算法的计算流程图如图 2所示。
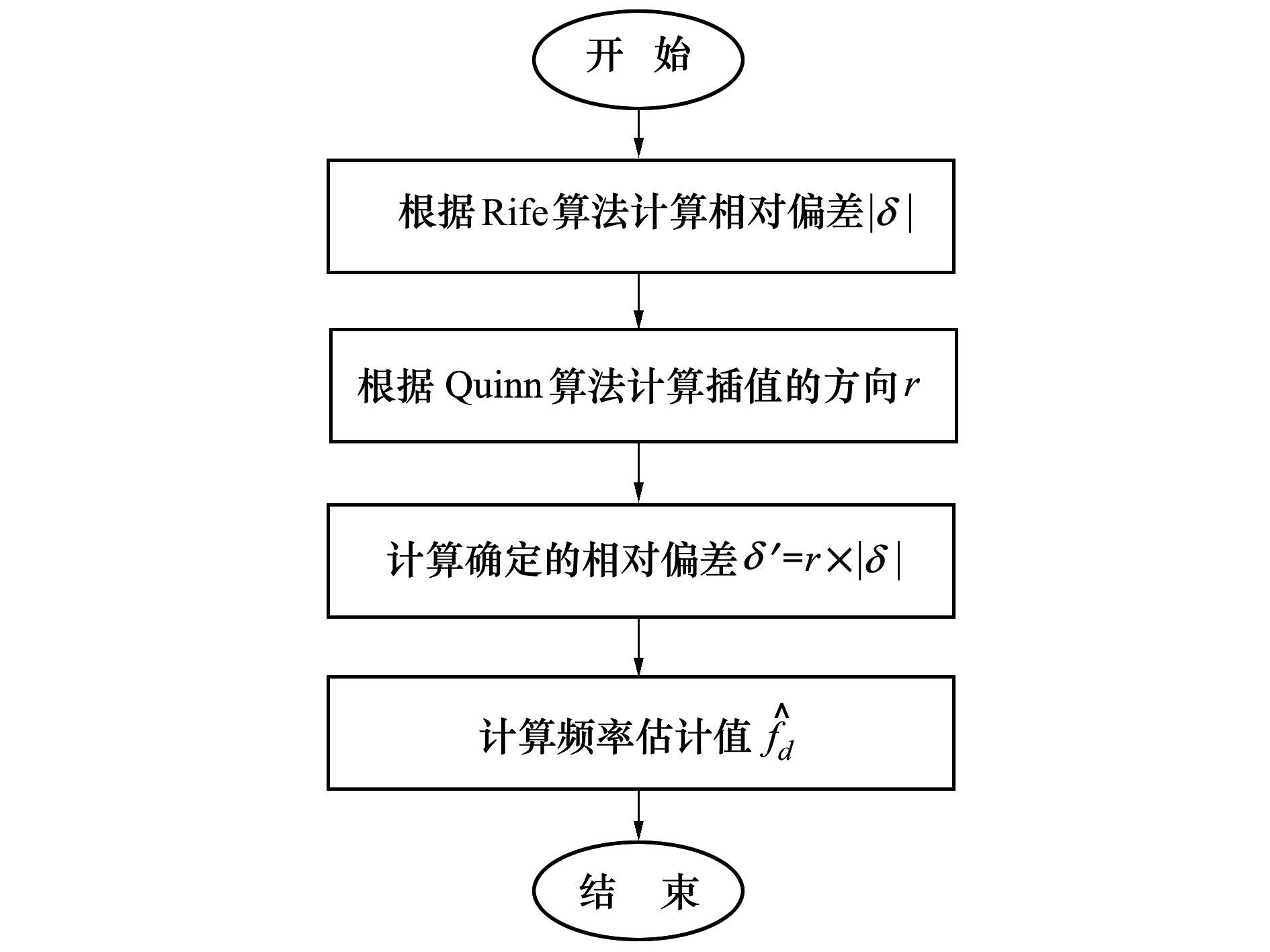
|
| 图 2 Q-Rife算法的计算流程图 |
Q-Rife算法融合了Rife算法和Quinn算法的优点, 克服了Rife算法中当δ较小时出现误差激增的致命缺点, 但依然无法解决|δ|较小时估计精度不高、性能差的问题。由1.3可知幅度相位联合内插算法在|δ|较小时保持较高的性能, 因此, 可以考虑在|δ|较小时使用幅相联合内插算法, 在|δ|较大时使用Q-Rife算法。
1.4.2 API-Q-Rife算法由于幅度相位联合内插算法在|δ|较小时频率估计较高, 所以当|δ|≤δR时, 采用幅相联合内插算法, 当δR<|δ|≤1/2时采用Q-Rife算法, 进而设计得到API-Q-Rife算法。这里, 引入了一个参数δR, 判决采用Q-Rife算法还是幅相联合内插算法, 在工程上一般根据先验信息进行设定门限值, 本文则通过MATLAB 2014a仿真出门限值大小。
基于上述API-Q-Rife算法, 计算的频率估计步骤如下:
Step1 根据幅度相位联合内插算法计算相对偏差[4]:
1) 记录FFT最大谱线及其两侧相邻2根谱线的坐标 (k0, X(k0)), (k0-1, X(k0-1)), (k0+1, X(k0+1)), 计算R0=Re (X(k0)X*(k0)), R1=Re (X(k0+1) X*(k0)), R-1=Re (X(k0-1)X*(k0));
2) 计算相对偏差:
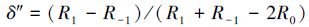
|
Step2 选择相对偏差:

|
(4) |
式中,δ′为1.4.1节Q-Rife算法得到的相对偏差。
Step3 将相对偏差δ*代入公式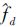
为了评估衡量频率估计算法的性能, 引入归一化频率估计误差, 定义为
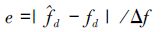
|
(5) |
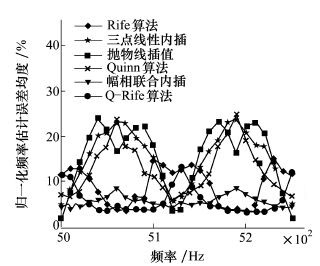
本节将对比各估计算法在不同频差下的仿真结果, 以证明本文所改进的频率内插算法的有效性。设Δf=125 Hz, 设置载波多普勒频差的仿真范围为[5 kHz, 5.25 kHz], 每个频点进行1 000次蒙特卡罗仿真实验。统计归一化频率估计误差均值, 衡量算法的估计精度。图 3给出了信噪比-20 dB时, 各算法的归一化频率估计误差均值曲线, 其中抛物线内插和三点线性内插为文献[8-9]中的算法。
|
| 图 3 信噪比-20 dB时归一化频率 |
将频率估计精度和算法稳定性可作为评判算法性能的2个指标。对于频率估计精度而言, 归一化频率估计误差均值越小, 估计精度越高; 反之, 估计精度越低。对算法稳定性而言, 归一化频率估计误差方差越小, 算法稳定性越好; 否则, 算法稳定性越差。为观察各算法的稳定性, 给出相同仿真条件下频率估计误差方差曲线, 如图 4所示。结合图 3和图 4可以看出在低信噪比条件下:①Rife算法对于靠近谱线的信号频差, 估计误差大, 且|δ|越小, 插值方向错误的概率越大, 算法的稳定性越差; |δ|越接近0.5, 估计误差越小, 算法稳定性越好。②三点线性内插算法和抛物线插值算法的性能相近:|δ|越大, 估计误差越大, 当|δ|≈0.5时估计误差最大; ③Quinn算法的频率估计误差随着|δ|的增大而增大, 且明显大于幅相联合内插和提出的Q-Rife算法。④幅相联合内插算法的频率估计误差随|δ|的增大呈现上升趋势, 在整个频率区间内误差的变化较为缓慢, 算法的稳定性较好。⑤改进的频率估计算法Q-Rife相对Rife算法提高了小|δ|下算法的估计精度, 相对Quinn算法提高了大|δ|下的估计精度, 且算法的稳定性优于Rife算法和Quinn算法。

|
| 图 4 信噪比-20 dB时归一化频率 |
图 5和图 6分别给出了10 dB的信噪比下归一化频率估计误差均值曲线及归一化频率估计误差方差曲线。由图 5和图 6可以看出:①在高信噪比条件下, 除了三点线性内插和抛物线插值算法外, 其余各频率估计算法误差较小, 稳定性比较好; ②三点内插算法除谱线位置外其余频点的估计误差均较大, 显然, 其不适于进行频率估计。
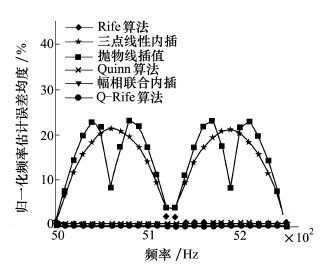
|
| 图 5 信噪比10 dB时归一化频率 |
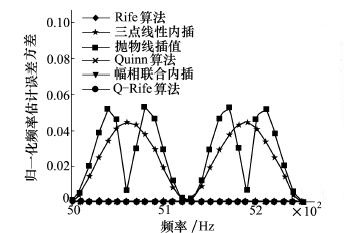
|
| 图 6 信噪比10 dB时归一化频率 |
综上所述, 幅相联合内插算法和改进的频率估计算法Q-Rife相对其他算法的性能较好。幅相联合内插算法和Q-Rife算法进一步融合互补:①|δ|≤1/3时, 幅相联合内插算法估计误差小, 改进的频率估计算法估计误差大; ②1/3<|δ|<1/2时, 幅相联合内插算法估计误差大, 改进的频率估计算法估计误差小。根据上面的分析, 选择δR=1/3, 在|δ|≤1/3时采用幅相联合内插算法, 1/3<|δ|<1/2时采用改进的频率估计算法, 进一步提高整个频率区间的估计精度。图 7和图 8给出了-20 dB时, 幅相联合内插算法, 改进的频率估计算法 (Q-Rife) 以及“幅相联合内插算法+改进的频率估计算法”(API-Q-Rife) 的归一化频率估计误差均值曲线及归一化频率估计误差方差曲线。
由图 7和图 8可以看出, 在信噪比为-20 dB时, API-Q-Rife算法整个频率区间内的估计误差明显小于幅相联合内插算法和Q-Rife算法, 且频率估计误差起伏最小, 算法精度和稳定度得到明显改善。
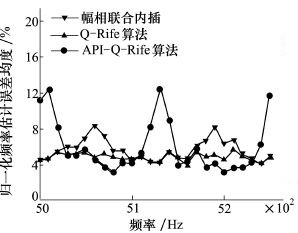
|
| 图 7 信噪比-20 dB时归一化频率 |
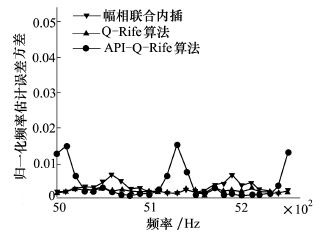
|
| 图 8 信噪比-20 dB时归一化频率 |
频率信息是信号分选、威胁识别、引导干扰的重要参数, 如何对截获的信号频率估计精度进行改善一直是设计接收端需要考虑的重要环节。通过融合利用Rife算法和Quinn算法的优点, 本文提出了一种改进的FFT频率插值估计的Q-Rife算法, 在减小频率估计误差的同时保证了算法的稳定性。在此基础上, 将改进的Q-Rife算法与幅相联合内插算法相结合, 进一步提出API-Q-Rife算法, 获得更优的频率估计性能。本文所提频率估计精度改善算法也可推广到FDMA等系统的频率估计, 有效改善频率估计精度。
| [1] | Lü Jun, Sun Weitao, Li Tong. Adaptive Algorithm Based on FFT for Frequency Estimation[C]//2013 International Conference on Measurement, Information and Control, 2013:883-886 |
| [2] |
姚如贵, 冯泽明, 赵雨, 王伶.
基于FFT的时域并行捕获算法研究[J]. 西北工业大学学报, 2013, 31 (3): 446–450.
Yao Rugui, Feng Zeming, Zhao Yu, Wang Ling. Proposing a Fast Time-Frequency-Domain Parallel Acquisition Algorithm Based on FFT[J]. Journal of Northwestern Polytechnical University, 2013, 31(3): 446–450. (in Chinese) |
| [3] | Lusin T, Agrez D. Minimum Bias Error of The Frequency Estimation with The Non-Parametric Method[C]//2013 IEEE International Instrumentation and Measurement Technology Conference, 2013:1232-1237 |
| [4] |
齐国清, 贾欣乐.
插值FFT估计正弦信号频率的精度分析[J]. 电子学报, 2004, 32 (4): 625–629.
Qi Guoqing, Jia Xinle. Accuracy Analysis of Frequency Estimation of Sinusoid Based on Interpolated FFT[J]. Acta Electronica Sinica, 2004, 32(4): 625–629. (in Chinese) |
| [5] | Stremfelj J, Agrez D. Nonparametric Estimation of Power Quantities in the Frequency Domain Using Rife-Vincent Windows[J]. IEEE Trans on Instrumentation and Measurement, 2013, 62(8): 2171–2184. DOI:10.1109/TIM.2013.2267433 |
| [6] |
谢胜, 陈航, 于平, 林少兴.
基于Quinn算法和相位差法的正弦波频率估计综合算法[J]. 信号处理, 2011, 27 (5): 71–75.
Xie Sheng, Chen Hang, Yu Ping, Lin Shaoxing. Sinusoid Wave Frequency Estimation Combined Algorithm Based on Quinn Algorithm and Phase Difference Correction Algorithm[J]. Journal of Signal Processing, 2011, 27(5): 71–75. (in Chinese) |
| [7] |
翟盛华.
一种高精度的频率估计算法研究[J]. 空间电子技术, 2014 (1): 64–67.
Zhai Shenghua. Research on A High Precision Frequency Estimation Algorithm[J]. Space Electronic Technology, 2014(1): 64–67. (in Chinese) |
| [8] |
龚国辉, 李思昆.
提高DSSS信号伪码相位测量精度的三点二次插值法[J]. 通信学报, 2007, 28 (2): 130–133.
Gong Guohui, Li Sikun. Improving DSSS Signal PN Code Phase Measurement Precision by 3-Points Quadratic Interpolation[J]. Journal on Communication, 2007, 28(2): 130–133. (in Chinese) |
| [9] |
刘银恩. 高精度频率估计算法研究[D]. 南京: 南京理工大学, 2007
Liu Yinen. Research on High Precision Frequency Estimation Algorithm[D]. Nanjing, Nanjing University of Science and Technology, 2007(in Chinese) |
2. School of Electronic and Control Engineering, Chang'an University, Xi'an 710064, China


