无人航行体, 包括无人机、无人飞艇、水下无人航行器等, 在现代战争中的地位越来越重要。基于多无人航行体的协同作战将在未来战争中发挥重要作用, 这一点已经成为世界各军事强国的共识。随着计算及通讯设备的小型化, 小型无人航行器机载计算机和通讯设备的计算能力和功能越来越强, 这使得多无人航行体执行协同作战任务成为可能。在协同作战任务中, 协同信息的共享和一致性是保障协同作战任务有效执行的关键。
多无人航行体网络中, 缺乏网络基础设施, 网络拓扑是时变的, 通信链路是不可靠的, 并且每个无人航行体节点的对周围节点的局部感知是动态变化的。因此, 需要研究新的一致性算法, 使无人航行体编队在执行任务时能够适应无线通信链路的特性、对感知到的环境变化做出合理响应、对不断变化的各节点状态信息进行统筹规划, 逐步达到一致性。多无人航行体通常采用无线自组织网络进行通信, 存在没有网络中心节点、无线链路丢包、时延不确定、网络拓扑频繁变化等不利因素, 多无人航行体的协同一致性算法一直是一个难题。
近年来, 随着多无人航行体的一致性算法广泛应用于无线传感器网络、无人机编队、多机器人编队等领域, 一致性算法的研究成为多学科领域的研究热点。信息一致性是协同控制的基本问题, 可以定义为多航行体在一定网络拓扑下通过一致性算法交换对协同任务有用的信息使各自状态达成一致, 往往借助图论、非负矩阵理论以及特征值扰动等进行研究。由于多无人航行体协同控制具有效率高、鲁棒性强、能耗低、无中心控制节点等优点, 比单一个体系统更加适用于未来战场以及救灾现场的复杂网络环境。多无人航行体协同控制的基本问题大致可以分为集合 (rendezvous)、编队 (formation)、群集 (flocking)、跟踪 (tracking) 等。
早期一致性算法的研究重点是算法的收敛性 (收敛条件、收敛速度、平衡态等)。Ren等[1-2]已经对一致性理论给出了很好的综述。影响系统收敛性能的主要因素是通信拓扑的代数连通性, 连通性越好, 协同信息交换越及时从而系统更稳定[3]。传统算法多利用单跳通信进行邻居节点的信息更新, 为了提高收敛速度, 二跳算法乃至多跳中继算法逐步被提出[4]。Olfati等[5]提出平均一致性, 即一致性平衡点为所有航行体初始信息状态的平均值, 并证明了当且仅当通信网络是强连通且平衡时编队可以达成平衡一致性。早期Ren等[6]在系统不考虑时延的情况下对固定通信拓扑网络拓扑图包含一个衍生树和切换拓扑子拓扑图包含一个衍生树达成一致性分别进行推导, 得到当系统包含衍生树的频率越高, 系统越稳定。
目前对一致性的研究大多是基于固定网络拓扑、无时延的条件设计的一、二阶的一致性算法, 而实际环境中往往是异步网络、动态拓扑并存在多种时延的非线性系统, 在这种复杂网络环境中想达成一致性往往需要高阶的算法[7]。多航行体协同控制中的时延主要分为交换信息的通信时延和反映个体对自身状态与邻居状态更新的不同步自时延2种。对时延的研究主要分为频域与时域2种[8]。频域法主要是通过Laplace变换将时域下的系统方程转换到频域里, 再通过Nyquist定理等对系统稳定性进行分析[9]。时域法则是通过Lyapunov类函数对连续系统的稳定性进行分析[10]。Lin等[11]通过构造Lyapunov-Krasovskii函数解决系统存在自时延和拓扑切换下一致性问题。网络化Euler-Lagrange系统分布式一致性研究通过将非线性控制理论和图论结合可以更高效地解决实际中协同控制问题。Ghapani等[12]提出一种基于多个不确定的拉格朗日系统下leader-followers的协同编队方法, 从而有效避免碰撞并使followers的速度收敛到leader。Mei等[13]在Euler-Lagrange系统下, 设计一种非连续控制器用于控制具有时变加速度的个体。
目前多无人航行体协同的一致性算法更多地被作为理论进行研究, 与实际应用的结合仍在探索之中。国内现阶段的研究主要在考虑时延[14]、异构网络[15]情况下的高阶分布式一致性算法。平均一致性[16-17]由于在同构与异构条件下均有良好收敛效果因而被广泛研究。
本文设计的基于马尔科夫随机场的多无人航行体的协同一致性算法在其他文献中目前尚没有采用, 目前已有的基于极大一致性算法与本文采取的方案类似, 但不尽相同, 本文方案具有如下优势:①大部分一致性算法中, 随着网络规模扩大, 收敛速度变慢。②大部分一致性算法主要进行平均运算, 远离参考基准的节点加入网络会增加偏差。而本文提出的算法在这2个方面有所改善。
1 多无人航行体协同任务描述多无人航行体的协同任务的目标是达成协作信息的一致性, 部署在每个无人航行器上的传感器可以获取其他节点状态, 并通过无线网络传播协作信息。当多无人航行体对协作信息的达成共识时, 就称它们达到一致性。
通常多无人航行体网络中, 无线网络环境是不可靠的, 每个节点的局部状态是动态变化的, 每个无人航行体很难获得一致、准确、完整的协作信息, 需要设计一致性算法使各个无人航行体对协作信息逐步达成一致。多无人航行体协同问题具体可以分为领航问题和纯分布问题。领航问题中, 选择网络中某个节点作为领航节点, 或者通过外部输入网络参考基准信息。纯分布问题中, 网络中没有参考节点, 节点之间通过协商对协作信息达成一致。就本文的方法而言, 领航问题视为纯分布问题的一种特例 (基准是给定的)。本文所设计的一致性算法在网络没有参考节点时可以达到全网的一致性, 但在网络有参考节点或者外部输入的参考基准时, 也同样适用。
2 基于马尔可夫随机场的分布一致性算法多无人航行体编队一般采用无线自组织网络进行通信, 在网络中没有通信基础设施, 节点是分布式的, 很难建立统一的参考基准。本文的协同一致性算法中, 将全网协作信息的总体效果等效于一个平均场, 使用该平均场作为虚拟参考基准。本文提出的一致性算法仅需要在邻居节点间交换协作信息, 由邻居节点间的一致达到全网络的一致性, 可以看出, 多无人航行体网络一致性的收敛过程具有空间马尔可夫性, 我们将基于空间马尔可夫随机场建立多无人航行体的协同一致性算法。根据马尔科夫随机场与吉布斯随机场的等价性, 通过引入邻居系统和团势能, 得到基于伊辛模型的能量函数, 并在此基础上给出采用能量最小化寻优的一致性算法。
2.1 网络通信关系模型考虑到多无人航行体网络一致性的收敛过程具有空间马尔可夫性, 采用邻域系统对多无人航行体进行建模。一个邻域系统N可以定义为
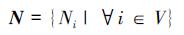
|
(1) |
Ni是编号为i的节点邻居节点集合, 其相邻关系有如下特点[18]:
1) 相邻关系是相互的。
2) 节点与自身不构成相邻关系。
多无人航行体组成的网络通常可以用图G=(V, E) 来描述, 其中V表示节点的集合, E表示节点间链路的集合。网络中各个节点间的相互作用可以用团的概念进行建模, 网络中的一个团C是节点集的一个子集。可以定义单节点团C1、双节点团C2, 三节点团C3等, 本文中主要关注C1和C2

|
(2) |
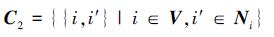
|
(3) |
将协作变量的取值定义为一个标签, 就可以用标签问题[18]对多无人航行体的一致性进行描述。标签集合可以是离散的或者连续的, 分配标签即为配置一个节点, 标签化是指从一个标签集合中分配一个标签给V中的每个节点。在实际中, 每个无人航行体的速度、位置等均可作为标签, 不失一般性, 将标签的取值空间取为实数域
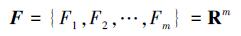
|
(4) |
式中,m为网络中节点的个数。全网协作变量可以表示如下
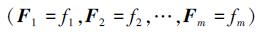
|
(5) |
式中,Fi=fi代表的事件是编号为i的节点获取本地协作变量值为fi。(5) 式可简写为F=f, 其中f是一个联合事件, 是F的一个配置。定义P(f) 为f的概率, 给节点i分配一个标签fi表明节点i获得变量值fi的概率为P(fi)。对于邻域系统N, F是在G上的马尔科夫随机场, 满足以下2个条件
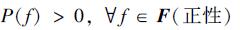
|
(6) |

|
(7) |
达到全网一致性的标准为所有节点分配了相同标签f:

|
(8) |
可以通过调整网络的配置求出P(fi=f) 的最大概率, 一致性也就可以被定义为寻找马尔科夫随机场的最大后验概率MAP (maximum a posteriori) 配置。
2.2 分布一致性的马尔可夫随机场模型马尔科夫随机场等同于吉布斯随机场, 因此节点配置服从吉布斯分布, 其形式如下:

|
(9) |
式中
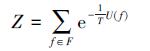
|
(10) |
是规格化的参数。T参数在物理层中代表温度。在大多数情况下中可以认为T=1。U(f) 是一个能量函数, 定义如下
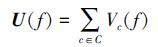
|
(11) |
可见, U(f) 就是在所有可能的团C上的团势能Vc(f) 之和[18], 它也可以表示为:
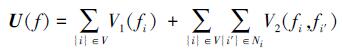
|
(12) |
在多无人航行体协同的一致性问题上, 本文中只考虑了C1团和C2团, 因此公式 (12) 可以重写如下
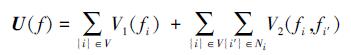
|
(13) |
根据公式 (9), 最小化能量函数U(f) 等同于最大化P(f) 的概率值。
考虑平均场理论中的伊辛模型, 伊辛模型系统中的总能量[19]为
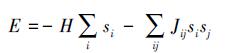
|
(14) |
式中,si为节点i的本地变量值, 在自组织网络中, 耦合矩阵Jij代表节点之间能够进行同步的邻居关系, 当Jij不等于0时, 表示2个节点i和j之间存在相互作用。比较公式 (13) 和公式 (14), 它们具有相同的表达式。伊辛模型的目标是使系统的总能量达到最小, 马尔可夫随机场的最大后验概率问题就等价于能量函数U(f) 最小化。本文的下一小节将寻找一种分布式的能量最小化算法来得到全网一致性的解决方案。
2.3 能量函数定义能量函数是多无人航行体的协同一致性问题的目标函数, 优化的目标是最小化能量, 并由此获得一致性问题的最佳解决方案。
如公式 (13) 中描述, 团的势能函数构成能量函数。参考文献[18], 双节点团C2的势能函数可以定义如下
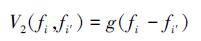
|
(15) |
式中,g(fi-fi′) 是一个单调减函数, 表示节点i和i′之间的偏差, 在本文中采用最常用的二次函数作为偏差函数, 可定义g(fi-fi′) 如下:
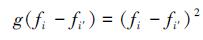
|
(16) |
在多无人航行体网络中, 本地节点与其他节点之间的协作变量可能会存在较大的偏差, 这是由节点发生故障后重启或者新节点的加入造成的, 这可能会在导致能量最小化时产生一个很大的修复因子, 这个因子会导致一致性过程产生较大波动, 难以在较短时间内回复到参考基准, 因此定义截断变量σ, 表示节点与邻居节点之间协作变量的方差, 将偏差函数修改为:
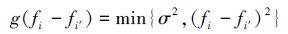
|
(17) |
g的导数也就变成如下形式:
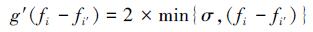
|
(18) |
对单节点团C1的势能函数, g依赖本地节点与参考基准偏差, 可被表示成如下二次方程的形式:

|
(19) |
式中,fR是参考基准。平均场理论认为对于给定个体, 所有其他个体对其的影响可以由一个平均作用近似获得[20], 用平均场定义节点i邻域系统的虚拟参考基准如下:

|
(20) |
前面的章节中提到过, 本文的一致性算法也适用于参考基准给定的情况, 当给定参考基准时fR仅仅与邻居节点的状态及其导数有关。最终我们得到完整的能量函数如下所示:
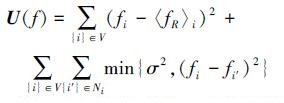
|
(21) |
能量函数U(f) 被定义为一个全局的量, 根据MAP方法, (21) 式的最小值点即为一致性问题的最优点。为寻找 (21) 式的最小值点, 需要收集每个节点的团势能来进行计算, 并找到最小化能量函数。在多无人航行体网络中, 网络拓扑不固定, 使用这种方法会产生很大的网络负载, 另外数据在网络中经过多跳传输时可能超时, 因此我们应该寻找一种分布式并行运行的能量函数最小化方法。
2.4 能量函数最小化方法由于存在截断因子, 能量函数U(f) 变成了一个非线性的函数。为了简化分析, 采用公式 (16) 中描述的双邻居节点团势能, 如下式:
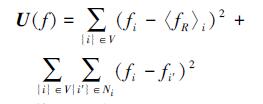
|
(22) |
由于最小值处一定是一个驻点, U(f) 的梯度向量必然等于0, 即下面的等式必然成立:
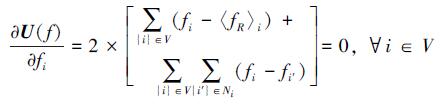
|
(23) |
为了求解公式 (23), 必须获得网络中每个节点的团势能, 这在多无人航行体网络中很难实现。因此我们对公式 (23) 更新如下

|
(24) |
我们定义
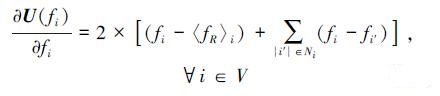
|
(25) |
也就是
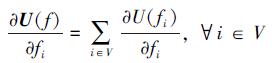
|
(26) |
根据公式 (23), 求得结果是一个梯度为0的驻点, 驻点有可能是局部极值点而不是全局最小值点, 但在本文中, 能量函数U(f) 是一个二次函数, 二次函数是严格凸函数, 在全局最多只有一个极值点[21], 因此根据公式 (23) 求解的最小值点就是全局最小值点。
根据公式 (25), U(f) 可以在网络中的每个节点上并行地更新。为获得全局能量函数的最小值, 只需要邻居信息, 计算每个节点的最小化能量函数。这样就通过每个节点局部的fi, 计算出全局最优化结果。由此我们得到了一个全分布式能量最小化算法。
在实际应用中, 无人航行体节点计算能力和功率都十分有限, 能量最小化函数的算法可以采用下面的规则进行迭代求解:
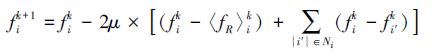
|
(27) |
式中,μ是一个数值很小的常数。由于公式 (27) 不涉及微积分元算, 仅涉及简单的算术运算和初等函数运算, 因此本文的一致性算法复杂度低、实用性强。
2.5 算法描述利用最小化能量函数的寻优方案, 最终形成本文的一致性算法。算法的关键是参考基准fR的求解方法, 根据前文所述, 可以利用平均场理论计算得到参考基准:平均场理论中, 可以利用邻居节点协作变量偏差与卡尔曼滤波算法得到fR。
假设多无人航行体网络包含M个节点, 本文一致性算法如下。
算法1:
1) 初始化;
2) 设置同步周期计时器;
3) 迭代计算直到满足收敛精度;
4) FOR第k次迭代;
5) 节点i, i=1:M, IN parallel;
6) 将本地第k-1的发送协作变量以及第k-1次迭代后收到所有邻居报文的协作变量打包成同步数据包;
7) 节点广播同步数据包到一跳邻居, 并记录发送的变量
8) 接收到一跳邻居的广播报文, 并记录接收的变量
9) 通过卡尔曼滤波器计算获得邻居节点间变量的偏差
10) 同步周期到, 同步计时器复位, 使用平均场算法计算参考基准的公式如公式 (20) 所示:
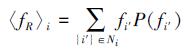
|
11) 基于参考基准计算公式 (21) 中的能量函数
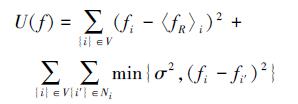
|
12) 计算最小化能量函数, 获得节点本地变量与虚拟参考基准差值, 调整本地变量值;
13) END parallel;
14) END FOR。
该算法充分利用了无线信道的广播特性, 在邻居节点间进行信息交互, 提高了效率, 减少了数据包的数量。
假设网络由M个节点构成, 传统单播双向交换信息的TPSN协议[22]在k次迭代中需要发送2*k*(M-1) 条消息量, 采用平均一致同步方式的ATSP协议[23]则需要发送3*k*M条消息量。在本文算法中, 如果采用本文算法计算虚拟参考基准, k次迭代需要的发送消息量为 (k+1)*M, 在网络规模很大、节点数目较多时, 收敛速度更快。本文算法在迭代过程中只需要存储一跳邻居发送的数据, 随着网络规模的增大, 本文算法在时间复杂度和空间复杂度方面将更具优势, 在达成一致性的过程中, 本文的算法能量消耗更少, 收敛速度更快。
3 收敛性说明为分析本文算法收敛性, 根据上文, 定义k次迭代后, 网络中所有邻居节点间的变量偏差的最大值e1-hop(k), 如公式 (28) 所示:
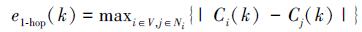
|
(28) |
式中, 节点i、j为一对邻居节点, Ci(k)、Cj(k) 分别是对应节点i、j在k次迭代后的本地变量值, 一致性达到的指标为任意相邻节点的变量偏差为0:e1-hop(k)=0, 那么任意一堆邻居节点间达到了一致。
偏差不仅仅存在于任意邻居节点之间, 在不相邻的节点间也存在, 因此定义k次迭代后, 网络中任意两个节点间的变量偏差最大值作为一致性评价指标, 如公式 (29) 所示:
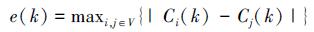
|
(29) |
那么一致性达到的指标为e(k)=0, 即任意2个节点间变量偏差为0, 达到了全网一致性。
在仿真过程中, 初始可设定每个节点协作变量取值于区间[0, 1], 且服从均匀分布, 然后选取e1-hop(k) 或者e(k) 作为一致性评判标准, 当e1-hop(k) 或者e(k) 达到很小时 (如10-6) 作为达到全网一致性的指标。
4 仿真与分析本文仿真包括两部分, Matlab仿真和动画仿真。Matlab仿真在Matlab 2009b环境下运行, 仿真场景为具有标准2-D网格3×3、4×4拓扑结构的节点构成, 并与目前主流的极大一致性算法的仿真结果相比较, 从而分析本文算法的性能。模拟仿真由C++语言编制而成, 能更直观地显示拓扑结构变化和一致性的结果。
4.1 基于matlab的仿真我们假设节点仅与其水平或垂直方向的一跳邻居进行交互, 即标准的4-邻居系统。在每一次同步迭代过程中, 网络中的每个节点与其邻居节点交换数据, 并更新各自的本地变量值。Matlab求解器的仿真步长设置为0.02 s, 当变量达到参考基准值±5%误差范围内认为达到了一致性, 仿真结果如下:
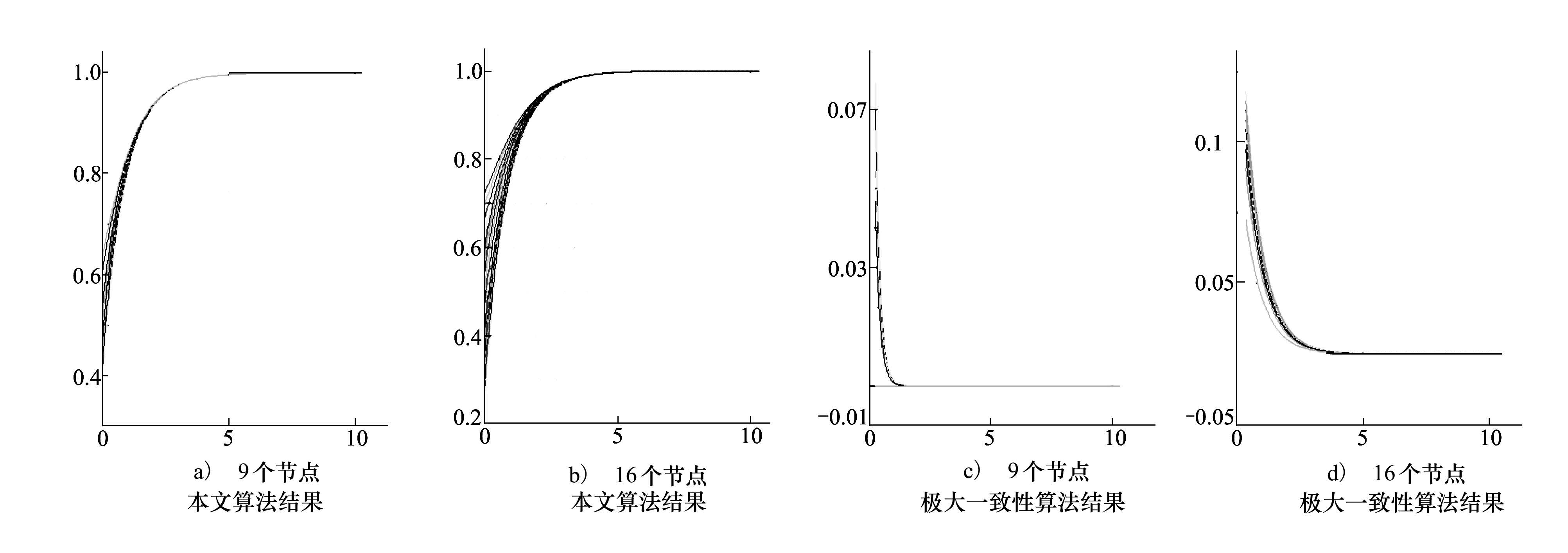
图 1中, 图a)、图b) 所示分别为本文算法在3×3、4×4的网格拓扑结构、网络没有外部基准的仿真结果, 计算可得, 分别在126、132迭代步时达到了一致性, 说明随着网络规模的扩大, 达到一致性的时间没有明显增加。图c)、图d) 分别为极大一致性算法在3×3、4×4的网格拓扑结构、没有外部基准的仿真结果, 计算可得, 在3×3场景中极大一致性算法在116迭代步达到一致性, 但在4×4场景中在227迭代步才达到一致性, 说明随着网络规模的扩大, 达到一致性的时间会急剧增加, 极大一致性算法的效率会大大降低。
|
| 图 1 没有外部基准情况下的仿真结果 |
根据前文所述, 本文算法虽然是在网络没有参考基准的情况下得到的, 但在网络中有参考节点、或者有外部输入的参考基准时, 本文算法也同样适用, 仿真结果如图 2、图 3所示。

|
| 图 2 有外部静态基准情况下的仿真结果 |
|
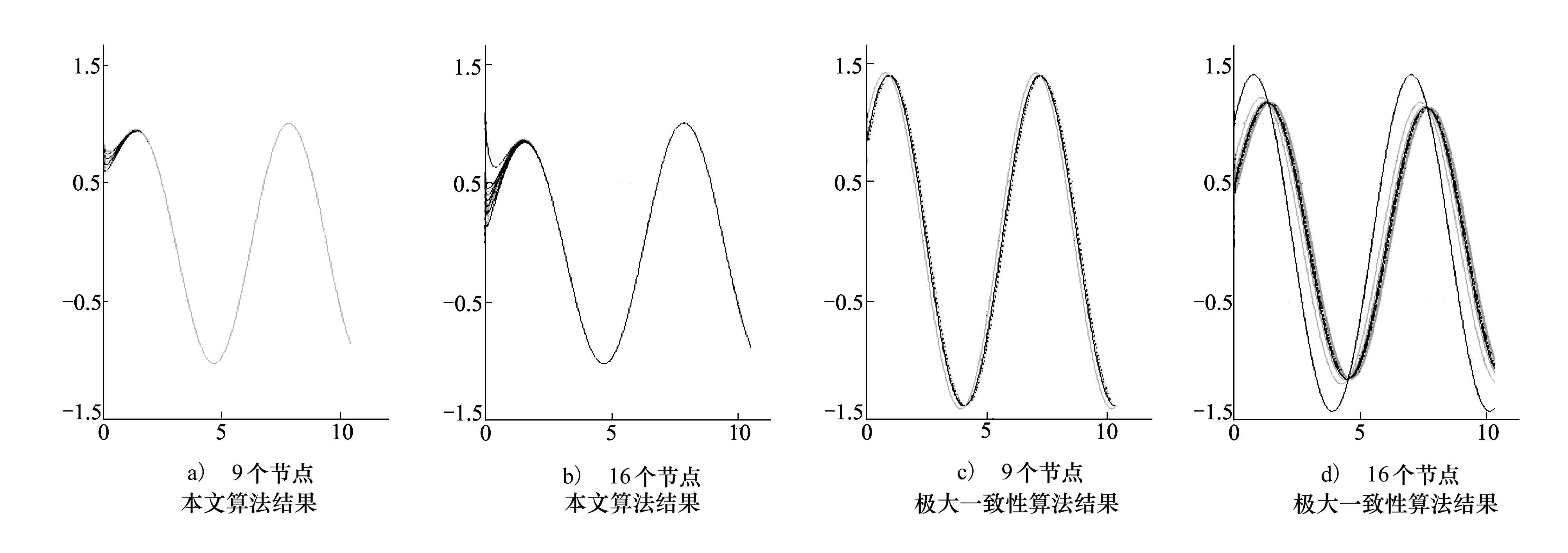
| 图 3 有外部动态态基准情况下的仿真结果 |
图 2中, 图a)、图b) 所示分别为本文算法在3×3、4×4的网格拓扑结构、网络有外部静态基准的仿真结果, 静态基准设置为1, 计算可得, 分别在125、130迭代步时达到了一致性, 说明随着网络规模的扩大, 达到一致性的时间没有明显增加。图c)、图d) 分别为极大一致性算法在3×3、4×4的网格拓扑结构、有外部静态基准的仿真结果, 计算可得, 在3×3场景中极大一致性算法在107迭代步达到一致性, 但在4×4场景中在216迭代步达到一致性, 与没有外部基准的情况类似, 虽然在9个节点时极大一致性算法的收敛速度略快于本文算法, 但随着网络规模的扩大, 极大一致性算法的效率大大降低。
图 3中, 图a)、图b) 所示分别为本文算法在3×3、4×4的网格拓扑结构、网络有外部动态基准的情况下的仿真结果, 动态基准设置为正弦信号, 计算可得, 分别在123、135迭代步时达到了一致性, 说明随着网络规模的扩大, 达到一致性的时间没有明显增加。图c)、图d) 分别为极大一致性算法在3×3、4×4网格拓扑结构、网络有外部动态基准的情况的仿真结果, 可以看出, 极大一致性算法的收敛结果有较大偏差, 收敛性能很差。
将上述仿真比较的结果总结如下:
从表 1可以看出,网络规模较小时极大一致性算法略有优势, 但随着网络规模的增大, 本文算法优势明显:收敛时间较低, 更加稳定。特别地, 在外部动态输入的情况下, 极大一致性算法的结果偏差很大。
| 算法 | 基准 | ||
| 无参考基准 | 静态参考基准 | 动态参考基准 | |
| 本文 | 126(9节点) 135(16节点) | 125(9节点) 130(16节点) | 123(9节点) 135(16节点) |
| 极大 一致性 | 116(9节点) 227(16节点) | 107(9节点) 216(16节点) | 偏差很大, 性能很差 |
利用C++语言编制MFC程序进行模拟仿真, 仿真结果更加直观。图 4中, 网络中有9个节点, 其中图a) 为初始化结果, 每个节点在不同的位置。图b) 为没有外部基准情况下利用本文算法达到的形成围绕虚拟基准点的盘旋过程。图c) 中, 拖动任何一个节点作为领航节点, 其他节点会自动调整跟随领航节点, 达到一致性。

|
| 图 4 一致性算法的MFC程序仿真结果 |
本文研究了多无人航行体的协同一致性问题, 提出一种基于马尔科夫随机场的协同一致性算法。本文所设计的一致性算法在网络没有参考节点时可以达到全网的一致性, 但在网络有参考节点或者外部输入的参考基准时, 本文算法也同样适用, 并与目前广泛采用的极大一致性算法进行了比较, 仿真结果表明, 在网络规模较大时, 本文算法具有更好的精度和更快的收敛时间, 本文算法优势明显。与现有的算法相比, 本文所提出的解决方案不依赖特定的参考节点, 并且只和邻居通信, 具有低负载、快速收敛、健壮、可靠的优点。
| [1] | Ren W, Beard R W, Atkins E M. A survey of Consensus Problems in Multi-Agent Coordination[C]//Proceedings of The 2005 American Control Conference Portland, USA, ACC, 2005:1859-1864 |
| [2] | Cao Y C, Yu W W, Ren W, Chen G R. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination[J]. IEEE Trans on Industrial Informatics, 2013, 9(1): 427–438. DOI:10.1109/TII.2012.2219061 |
| [3] | Olfati-Saber R. Ultrafast Consensus in Small-World Networks[C]//American Control Conference IEEE, 2005:2371-2378 |
| [4] |
彭换新, 戚国庆, 盛安冬.
基于有向通信拓扑的高阶分布式一致性算法[J]. 计算机应用, 2013, 33 (10): 2757–2761.
Peng Huanxin, Qi Guoqing, Sheng Andong. A High-Order Distributed Consistency Algorithm under Directed Communication Topology[J]. Journal of Computer Applications, 2013, 33(10): 2757–2761. DOI:10.3724/SP.J.1087.2013.02757 (in Chinese) |
| [5] | Olfati-Saber R, Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays[J]. IEEE Trans on Automatic Control, 2004, 49(9): 1520–1533. DOI:10.1109/TAC.2004.834113 |
| [6] | Ren W, Beard R W. Consensus Seeking in Multi-Agent Systems under Dynamically Changing Interaction Topologies[J]. IEEE Trans on Automatic Control, 2005, 50(5): 655–661. DOI:10.1109/TAC.2005.846556 |
| [7] | Yu W, Chen G, Ren W, et al. Distributed Higher Order Consensus Protocols in Multi-agent Dynamical Systems[J]. IEEE Trans on Circuits & Systems I Regular Papers, 2011, 58(8): 1924–1932. |
| [8] | Meng Z Y, Ren W, Cao Y C, Zheng Y. Leaderless and Leader-Following Consensus with Communication and Input Delays Under a Directed Network Topology[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B:Cybernetics, 2011, 41(1): 75–88. DOI:10.1109/TSMCB.2010.2045891 |
| [9] | Yang W, Bertozzi A L, Wang X F. Stability of a Second Order Consensus Algorithm with Time Delay[C]//Proceedings of the 47th Conference on Decision and Control, Cancun, Mexico, 2008:2926-2931 |
| [10] | Lin P, Jia Y M. Consensus of a Class of Second-Order Multi-Agent Systems with Time-Delay and Jointly-Connected Topologies[J]. IEEE Trans on Automatic Control, 2010, 55(3): 778–784. DOI:10.1109/TAC.2010.2040500 |
| [11] | Lin P, Jia Y M. Multi-Agent Consensus with Diverse Time-Delays and Jointly-Connected Topologies[J]. Automatica, 2011, 47(4): 848–856. DOI:10.1016/j.automatica.2011.01.053 |
| [12] | Ghapani S, Mei J, Ren W. Flocking with a Moving Leader for Multiple Uncertain Lagrange Systems[C]//American Control Conference (ACC), 2014:3189-3194 |
| [13] | Mei J, Ren W, Ma G F. Distributed Coordinated Tracking with a Dynamic Leader for Multiple Euler-Lagrange Systems[J]. IEEE Trans on Automatic Control, 2011, 56(6): 1415–1421. DOI:10.1109/TAC.2011.2109437 |
| [14] |
薛瑞彬, 宋建梅, 张民强.
具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究[J]. 兵工学报, 2015, 36 (3): 492–502.
Xue Ruibin, Song Jianmei, Zhang Minqiang. Research on Distributed Multi-Vehicle Coordinated Formation Flight Control with Coupling Time-Delay and Jointly-Connected Topologies[J]. Acta Armamentarii, 2015, 36(3): 492–502. (in Chinese) |
| [15] |
徐杨, 李响, 常宏, 等.
复杂网络特性对大规模多智能体协同控制的影响[J]. 软件学报, 2012 (11): 2971–2986.
Xu Yang, Li Xiang, Chang Hong, et al. Effects of Complex Network Characters on the Coordination Control of Large-Scale MultiAgent System[J]. Journal of Software, 2012(11): 2971–2986. (in Chinese) |
| [16] |
康玉婷, 李琳.
马尔科夫切换拓扑下时滞多智能体系统的平均一致性[J]. 江南大学学报:自然科学版, 2014, 13 (5): 563–567.
Kang Yuting, Li Lin. Average Consensus of a Class of Multi-Agent Systems with Markov Switching Topology and Time-Delay[J]. Joural of Jiangnan University (Natural Science Edition), 2014, 13(5): 563–567. (in Chinese) |
| [17] |
孙一杰, 张国良, 张胜修, 等.
一类异构多个体系统的广义平均一致性分析[J]. 动力学与控制学报, 2015, 22 (4): 154–160.
Sun Yijie, Zhang Guoliang, Zhang Shengxiu, et al. Generalized Average Consensus Analysis for a Class of Heterogeneous Multi-agent Systems in Directed Topology[J]. Journal of Dynamics and Control, 2015, 22(4): 154–160. (in Chinese) |
| [18] | Li S Z. Markov Random Field Modeling in Image Analysis[M]. London: Springer, 2009. |
| [19] | Baierlein R. Thermal Physics[M]. Britain: Cambridge University Press, 1999. |
| [20] | Chandler D. Introduction to Modern Statistical Mechanics[M]. Britain: Oxford University Press, 1987. |
| [21] | Borwein J M, Lewis A S. Convex Analysis and Nonlinear Optimization:Theory and Examples[M]. Germany: Springer, 2010. |
| [22] | Ganeriwal S, Kumar R, Srivastava M B. Timing-Sync Protocol for Sensor Networks[C]//Proceedings of the 1st ACM International Conference on Embedded Networked Sensor Systems, 2003:138-149 |
| [23] | Wu J, Jiao L, Ding R. Average Time Synchronization in Wireless Sensor Networks by Pairwise Messages[J]. Computer Communications, 2012, 35(2): 221–233. DOI:10.1016/j.comcom.2011.09.007 |


