2. 西北农林科技大学 理学院, 陕西 杨凌 712100
随着科学技术和计算机水平的不断发展, 数值分析在科学与工程界发挥着越来越重要的作用。在具体的应用过程中, 随着处理动力学问题难度的不断加大, 需要更好的数值方法作为基础。科研人员对数值算法的发展要求是不仅与精确解误差要尽可能小, 更重要的是要保持长时间数值稳定性以及能够体现动力学系统内在几何性质。冯康等[1]在“数值算法应尽可能保持原问题的本质特征”的原则下, 基于辛几何原理,提出和发展了一套哈密顿系统辛算法, 取得了一系列显著的成果。然而在处理偏微分发展方程时, 却没有好的方法保证空间离散后的方程组仍保持哈密顿特性。针对辛算法处理偏微分方程时的缺陷, 依照保结构思想, Marsden[2]和Bridges[3-4]分别提出了无穷维保守哈密顿系统的多辛结构和多辛算法的理论。作为辛算法的直接推广, 近年来, 由于在理论和大量的数值实验中展现出了诸如精度高、稳定性好以及保结构等数值特性, 多辛算法受到了学术界的广泛关注:Moore等[5]提出和发展了多辛积分的后向误差分析理论; 王雨顺等[6-8]在各种离散格式的构造, 如高阶算法、保能量、保动量算法等方面做了大量工作; 洪佳林等[9]研究了随机非线性发展方程的多辛算法; 胡伟鹏等[10]将多辛算法引入到应用力学领域的非保守系统, 提出和发展了广义多辛算法。
非线性孤子理论在物理学、力学及自然科学的很多领域得到了大量的应用。Landau-Ginzburg-Higgs方程是一个典型的非线性发展方程[11], 胡伟鹏等[12]研究了其隐式多辛Runge-Kutta离散格式的数值行为, 给出了算法高精度、长时间稳定和保结构等数值特性, 并依照广义多辛理论的思路[13], 研究了微扰效应对孤立波传播过程中振幅和波速的影响。众所周知, 隐式格式在每一时间步都要迭代求解复杂的非线性方程(组), 计算效率将受到影响。本文将构造一种Landau-Ginzburg-Higgs方程的显式多辛傅里叶拟谱格式, 并对这种格式的数值特性进行了研究。
1 Landau-Ginzburg-Higgs方程的多辛形式依照Bridges构造多辛形式的思想[4], 其基本思路是通过引入适当的正则变量, 将高阶偏微分方程(组)系统降阶为一阶偏微分方程组对称形式, 并通过哈密顿函数来得到标准的多辛方程组。
Landau-Ginzburg-Higgs方程的形式如下
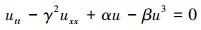
|
(1) |
式中,α, β, γ∈R为系数。
通过引入正则动量v=∂tu, w=∂xu可得到Landau-Ginzburg-Higgs方程(1)的一阶多辛偏微分方程组
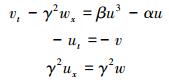
|
(2) |
如定义反对称系数矩阵M和K如下

|
则(2)式可以写为标准的多辛形式
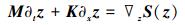
|
(3) |
式中,z=[u, v, w]T∈R3为状态变量, 哈密顿函数为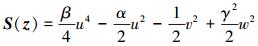
之所以称一阶偏微分方程组(3)为多辛形式, 因为其满足多辛守恒律。依据多辛积分理论[4], 其多辛守恒律具体形式可以表示为
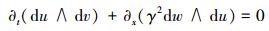
|
(4) |
式中,∧为外积算子。
由于系数矩阵M和K的反对称性, 通过(3)式两边分别对∂tz和∂xz做内积, 还可以得到另外2种重要的守恒量:局部能量和局部动量守恒律。依照多辛积分理论[4], 局部能量守恒律的具体形式为
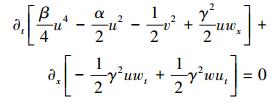
|
(5) |
局部动量守恒律的具体形式为
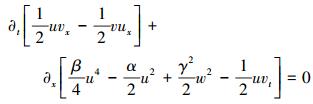
|
(6) |
局部保结构算法的核心思想是把整个时间层上所保的结构推广到局部, 使得算法能在局部领域和每个点上保持守恒性质, 从而克服不同边界条件的限制。这正是多辛算法在处理偏微分方程时的优势所在, 可以应用到更广泛的领域。在算例分析中将分析(5)式和(6)式的守恒性质。
2 多辛形式的傅里叶拟谱离散格式对多辛偏微分方程组(3)在空间方向进行傅里叶拟谱离散、在时间方向进行辛欧拉离散[14], 可得到一种多辛离散方法, 即傅里叶拟谱离散格式。
首先做一些定义, 假设u(x, t)在空间[a, b]上可微, 区间长度为L=b-a。时间步长和空间步长分别为Δx和Δt。将空间N等分(其中N为偶数), 则分点可以表示为xi=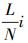

|
(7) |
式中,μ=2π/(b-a)。
考虑对多辛形(3)式空间方向进行傅里叶拟谱离散, 可得
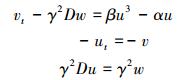
|
(8) |
如将(8)式写成紧凑形式, 则有
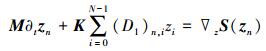
|
(9) |
对半离散格(9)式的变分方程两边取dzn的外积, 由矩阵Szz(zn)的对称性, 可得到傅里叶拟谱离散格(9)式满足N个半离散多辛守恒律
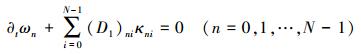
|
(10) |
式中
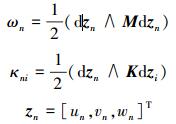
|
(9)式是空间方向采用傅里叶拟谱方法的半离散形式, 如要得到全离散格式则需将时间方向进一步离散。本文采用辛欧拉格式在时间方向对(9)式进行离散, 可得到
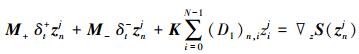
|
(11) |
式中矩阵M+和M-满足关系
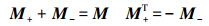
|
δt+和δt-分别为向前差分和向后差分算子
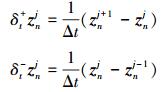
|
与(9)式类似, 对全离散格(11)式的变分方程两边取dznj的外积, 由矩阵Szz(znj)的对称性, 可得到傅里叶拟谱离散格(11)式满足N个离散多辛守恒律
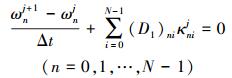
|
(12) |
式中
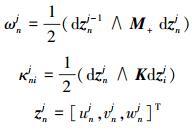
|
此处取M+=M-=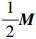
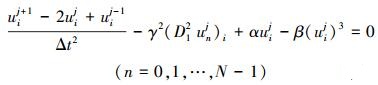
|
(13) |
由于格式(13)满足离散多辛守恒律(12)式, 则可称其为多辛离散格式。在下一节中将考察离散格式(13)的数值特性。
3 数值算例为了研究离散格式(13)的数值行为, 本节将给出一些算例结果。不同于隐式格式, (13)式为显式格式, 这避免了复杂的迭代过程, 计算效率将得到提高。
考虑Landau-Ginzburg-Higgs方程(2)非周期边界的扭状孤波解如下
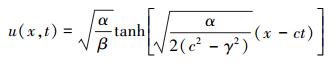
|
(14) |
式中,c表示孤波波速。(13)式是一个3层的离散格式, 在计算过程中应给出前2层初值条件如下
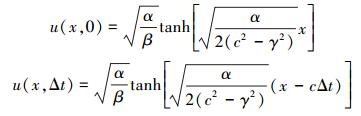
|
(15) |
数值计算中选取参数α=-2, β=-2, γ=1, 波速c为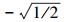
图 1给出了传播过程中不同时刻(t=5, t=10, t=15, t=20)的波形图, 其中实线为精确解的值, “·”号为数值解的值。由图 1可以看出, 在孤波传播的各个时刻, 数值解和精确解都吻合良好, 没有随着时间增长出现明显偏差。这说明离散格式(13)很好地模拟了孤波演化过程, 保持了孤波的基本几何性质。值得一提的是, 本文中格式(13)在模拟非周期边界孤波演化过程中给出了较好的结果。

|
| 图 1 不同时刻数值解和精确解的波形图(其中实线为精确解, “·”为数值解) |
为了研究数值精度, 记录了孤波传播过程中不同时刻的数值误差, 在t=jΔt时刻的最大数值误差可以表达如下
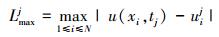
|
(16) |
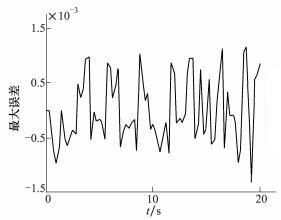
式中,u(xi, tj)和uij分别表示在x=a+iΔx, t=jΔt处的精确解和数值解。图 2给出了t∈[0, 20]时的最大误差变化情况。从图中可以看出, 误差值在0附近波动, 保持在[-1.5×10-3, 1.5×10-3]范围内, 没有随着时间增长出现明显的误差累积过程, 这体现了多辛保结构算法的稳定性。
|
| 图 2 不同时刻数值解的最大误差 |
为了进一步验证多辛离散格式(13)具有保持系统局部特性的能力, 记录了离散局部能量和动量守恒律误差。用Emax和Imax分别表示离散局部能量最大误差和离散局部动量最大误差, 定义不同时刻的局部守恒量最大误差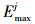

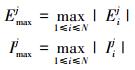
|
(17) |
式中,Eij和Iij分别表示在x=a+iΔx, t=jΔt处的离散局部守恒量的数值解。图 3给出了不同时刻局部能量和局部动量的最大误差。从图中可以看出局部能量最大误差保持在10-5量级、局部动量最大误差保持在10-6量级, 这说明多辛离散格(13)式可以很好的保持动力系统局部性质。它是局部保结构格式, 不依赖于边界条件的限制, 当边界条件满足时, 自然可以推广到整体守恒量的保持。

|
| 图 3 不同时刻数值解局部能量和局部动量最大误差 |
多辛方法是一种局部保结构算法, 强调保持离散动力系统的局部特性, 其提出和发展拓宽了保结构算法的适用性。本文基于多辛理论, 得到了Landau-Ginzburg-Higgs方程的一种显式多辛拟谱离散格式, 给出了其多辛守恒律、局部能量守恒律和局部动量守恒律的表达形式。数值模拟显示了该离散格式的优越性:在数值计算中很好地保持了动力系统基本几何性质; 随着孤波演化的过程中没有出现明显误差累计过程; 系统局部特性(局部能量和局部动量守恒律)保持良好。数值结果体现了高效、稳定的数值行为, 这也正是多辛算法的优势所在。
| [1] | Feng K. Difference Schemes for Hamiltonian Formulism and Symplectic Geometry[J]. Journal of Computational Mathematics, 1986, 4(3): 279–289. |
| [2] | Marsden J E, Shkoller S. Multisymplectic Geometry, Covariant Hamiltonians, and Water Waves[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1999, 125(3): 553–575. DOI:10.1017/S0305004198002953 |
| [3] | Bridges T J. Multi-Symplectic Structures and Wave Propagation[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121(1): 147–190. DOI:10.1017/S0305004196001429 |
| [4] | Bridges T J, Reich S. Multi-Symplectic Integrators:Numerical Schemes for Hamiltonian PDEs that Conserve Symplecticity[J]. Physics Letters A, 2001, 284(4/5): 184–193. |
| [5] | Moore B, Reich S. Backward Error Analysis for Multi-Symplectic Integration Methods[J]. Numerische Mathematik, 2003, 95(4): 625–652. DOI:10.1007/s00211-003-0458-9 |
| [6] | Wang Y S, Wang B, Qin M Z. Numerical Implementation of the Multisymplectic Preissman Scheme and Its Equivalent Schemes[J]. Applied Mathematics and Computation, 2004, 149(2): 299–326. DOI:10.1016/S0096-3003(03)00080-8 |
| [7] | Wang Y S, Wang B. High-Order Multi-Symplectic Schemes for the Nonlinear Klein-Gordon Equation[J]. Applied Mathematics and Computation, 2005, 166(3): 608–632. DOI:10.1016/j.amc.2004.07.007 |
| [8] | Cai J X, Wang Y S. Local Structure-Preserving Algorithms for the "Good" Boussinesq Equation[J]. Journal of Computational Physics, 2013, 239(239): 72–89. |
| [9] | Jiang S S, Wang L J, Hong J L. Stochastic Multi-Symplectic Integrator for Stochastic Nonlinear Schrdinger Equation[J]. Communications in Computational Physics, 2013, 14(2): 393–411. DOI:10.4208/cicp.230212.240812a |
| [10] | Hu W P, Deng Z C, Han S M, Zhang W R. Generalized Multi-Symplectic Integrators for a Class of Hamiltonian Nonlinear Wave PDEs[J]. Journal of Computational Physics, 2013, 235(4): 394–406. |
| [11] |
莫嘉琪, 王辉, 林一骅.
广义Landau-Ginzburg-Higgs方程孤子解的扰动理论[J]. 物理学报, 2005, 54 (12): 5581–5584.
Mo Jiaqi, Wang Hui, Lin Yihua. Perturbation Theory of Soliton Solution for the Generalized Landau-Ginzburg-Higgs Equation[J]. Acta Physica Sinica, 2005, 54(12): 5581–5584. (in Chinese) |
| [12] | Hu W P, Deng Z C, Han S M, Fan W. Multi-Symplectic Runge-Kutta Methods for Landau-Ginzburg-Higgs Equation[J]. Applied Mathematics and Mechanics, 2009, 30(8): 1027–1034. DOI:10.1007/s10483-009-0809-x |
| [13] |
胡伟鹏, 张宇, 邓子辰.
微扰Landau-Ginzburg-Higgs方程的保结构数值分析[J]. 西北工业大学学报, 2012, 30 (6): 957–960.
Hu Weipeng, Zhang Yu, Deng Zichen. Structure-Preserving Analysis of Perturbed Landau-Ginzburg-Higgs Equation[J]. Journal of Northwestern Polytechnical University, 2012, 30(6): 957–960. (in Chinese) |
| [14] | Chen J B. Symplectic and Multisymplectic Fourier Pseudospectral Discretizations for the Klein-Gordon Equation[J]. Letters in Mathematical Physics, 2006, 75(3): 293–305. DOI:10.1007/s11005-005-0045-3 |
2. College of Science, Northwest A & F University, Yangling 712100, China


