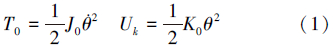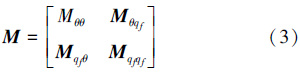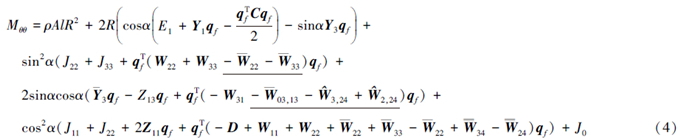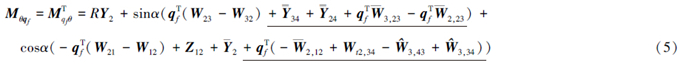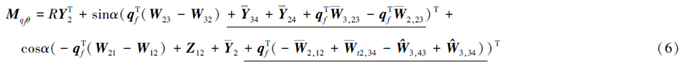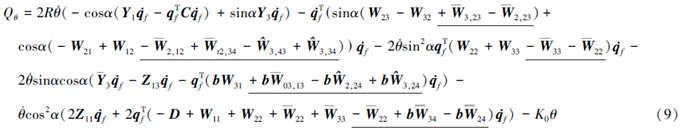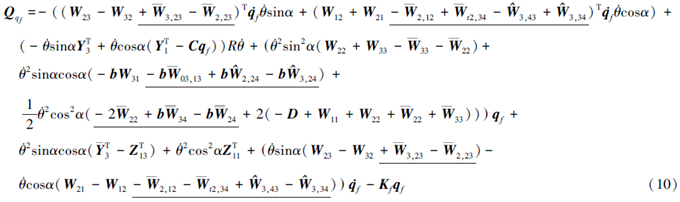文献[1, 2]针对非惯性系下大范围运动为已知的柔性梁结构进行了研究，在此类问题中刚体运动是作为已知运动出现的，表征刚体运动的坐标并不出现在系统的动力学方程中，因而实际上这类刚-柔耦合动力学研究的是单向问题，即只考虑了大范围运动对柔性结构的影响，而未考虑柔性体的变形对刚体运动的影响。而刚体运动规律未知的刚-柔耦合结构，也大量存在于实际工程结构中，如给定驱动力矩的柔性机械臂等结构。因而这类考虑刚-柔部件之间相互耦合作用的动力学问题也受到研究者的重视[3, 4, 5]。同时，对中心刚体-卷簧-柔性梁这类典型结构，有研究者进行了一些理论和实验研究[6, 7]。这些研究在一定程度上揭示了刚-柔耦合问题的特性，为工程实际应用做好了理论准备。
但是以往研究未考虑完全的几何非线性变形模式，其动力学方程以及实验比较是建立在一次耦合模型基础上的，因而只探讨了零次模型和一次耦合模型的差异,以及耦合模型与刚体模型之间的差异，并未探讨耦合模型之间的差异。此外，以往研究大多集中于平面结构的刚-柔耦合问题，而未涉及空间结构的刚-柔耦合问题。因此本文将对上述问题做一深入的研究。
1 空间柔性梁的刚-柔耦合动力学特性分析考虑一固结在旋转中心刚体上的空间悬臂柔性梁，如图 1所示。
 |
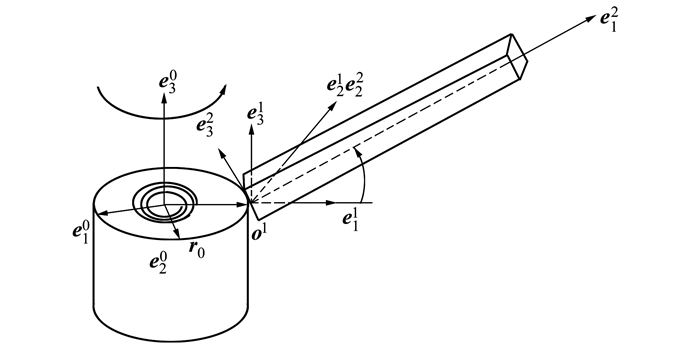| 图 1 中心刚体-空间悬臂梁-扭簧组成的空间刚-柔耦合结构 |
中心体半径为R,转角为θ,角速度为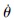
,角加速度为
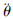,中心刚体的转动惯量为J0,中心刚体与机架之间装有刚度为K0的扭转弹簧。由于大范围运动规律未知,取系统的广义坐标为
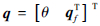,记中心刚体动能和扭转弹簧势能分别为
考虑了柔性梁的纵向伸缩、横向弯曲、侧向弯曲及扭转变形产生的几何非线性因素对变形耦合的影响后,本文精确模型较一次耦合模型增加了划线项;在柔性梁的纵向变形中计及了耦合变量,保留了变形位移偏导数的二次耦合变量后,使得本文精确模型和一次耦合模型均含有附加项C、D。而零次模型不含有附加项C、D及划线项。
取梁的物理参数:长度l为10 m,横截面积A为4×10-4m2,横截面的惯性矩Iyy为4×10-7m4,Izz为2×10-7m4,极惯性矩Ipp为Iyy+Izz,弹性模量E为7×1010N/m2,泊松比μ=0.33,扭转弹性模量G=
,密度ρ为3×103 kg/m3,倾角α为π/6,中心刚体半径R为1 m。
计算仿真结果表明,当初始角增大后,转动速度有较大增加,柔性梁的高阶频率(第三阶)被激发出来,但柔性体依旧对中心刚体的振动影响较小,表现为中心体转角对应的频谱图第二、三阶频率的幅值相对很小。3种模型的第二、三阶频率出现差别,第一阶频率依旧相同,均为0.110 Hz,第二阶频率,零次模型为1.672 Hz,一次耦合模型为1.703 Hz,本文精确模型为1.688 Hz;第三阶频率,零次模型为4.750 Hz,一次耦合模型为4.781 Hz,本文精确模型为4.766 Hz。当转速增加后,耦合项C、D使得一次、本文模型的各阶频率较零次模型有所增加,体现出动力刚化现象,而本文精确模型考虑了划线的新增耦合项后,各阶频率又低于一次模型,说明新增耦合项有使刚度降低的“软化”趋势。
改变K0、J0、R以获得不同刚柔投影刚度比Kpt、刚柔投影惯量比Jpt,比较不同初始角下的各阶频率如表 1、表 2所示。
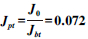时,初始角对系统频率的影响 (K0=200 N·m/rad,J0=30 kg·m2,R=1 m,
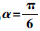, N:不存在)
| 参数 | 初始角度/rad | |||
| 0.01 | 0.2 | 0.5 | 1 | |
| 零次模型峰值角速度/(rad·s-1) | 0.010 | 0.195 | 0.488 | 0.976 |
| 一次模型峰值角速度/(rad·s-1) | 0.010 | 0.195 | 0.484 | 0.970 |
| 本文模型峰值角速度/(rad·s-1) | 0.010 | 0.196 | 0.487 | 0.974 |
| 零次模型第一阶频率/Hz | 0.109 | 0.109 | 0.109 | 0.109 |
| 一次模型第一阶频率/Hz | 0.109 | 0.109 | 0.109 | 0.109 |
| 本文模型第一阶频率/Hz | 0.109 | 0.109 | 0.109 | 0.109 |
| 零次模型与本文模型第一阶频率相对误差/% | 0 | 0 | 0 | 0 |
| 一次模型与本文模型第一阶频率相对误差/% | 0 | 0 | 0 | 0 |
| 零次模型第二阶频率/Hz | 1.688 | 1.688 | 1.688 | 1.672 |
| 一次模型第二阶频率/Hz | 1.688 | 1.688 | 1.688 | 1.703 |
| 本文模型第二阶频率/Hz | 1.688 | 1.688 | 1.688 | 1.688 |
| 零次模型与本文模型第二阶频率相对误差/% | 0 | 0 | 0 | 0.924 |
| 一次模型与本文模型第二阶频率相对误差/% | 0 | 0 | 0 | 0.924 |
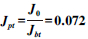时,初始角对系统频率的影响(K0=500 N·m/rad,J0=30 kg·m2,R=1 m,
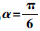, N:不存在)
| 参数 | 初始角度/rad | |||
| 0.01 | 0.2 | 0.5 | 1 | |
| 零次模型峰值角速度/(rad·s-1) | 0.018 | 0.356 | 0.892 | 1.787 |
| 一次模型峰值角速度/(rad·s-1) | 0.018 | 0.353 | 0.882 | 1.742 |
| 本文模型峰值角速度/(rad·s-1) | 0.018 | 0.354 | 0.891 | 1.761 |
| 零次模型第一阶频率/Hz | 0.156 | 0.156 | 0.156 | 0.156 |
| 一次模型第一阶频率/Hz | 0.156 | 0.156 | 0.156 | 0.156 |
| 本文模型第一阶频率/Hz | 0.156 | 0.156 | 0.156 | 0.156 |
| 零次模型与本文模型第一阶频率相对误差/% | 0 | 0 | 0 | 0 |
| 一次模型与本文模型第一阶频率相对误差/% | 0 | 0 | 0 | 0 |
| 零次模型第二阶频率/Hz | 1.719 | 1.719 | 1.703 | 1.688 |
| 一次模型第二阶频率/Hz | 1.719 | 1.719 | 1.734 | 1.781 |
| 本文模型第二阶频率/Hz | 1.719 | 1.719 | 1.719 | 1.734 |
| 零次模型与本文模型第二阶频率相对误差/% | 0 | 0 | 0.908 | 2.704 |
| 一次模型与本文模型第二阶频率相对误差/% | 0 | 0 | 0.914 | 2.704 |
不论刚柔投影刚度比、刚柔投影惯量比如何变化,随着初始转角的增大,造成角速度波动变大,使其峰值增加,刚体运动范围变大,因而耦合项C、D的作用逐渐明显。在初始角增大后,一次、本文模型的高阶频率(第二、三阶频率)逐渐增加,体现出动力刚化现象,而零次模型不能体现出动力刚化现象,其高阶频率降低,一次、本文模型的高阶频率均高于零次模型。由于本文模型新增耦合项的“软化”作用,使得本文精确模型的高阶频率低于一次耦合模型。
随着卷簧刚度的增加,即刚-柔投影刚度比的增加,在较小的初始角下,也造成角速度波动变大,其峰值增加。在相同初始角下,刚-柔投影刚度比较大的时候,3种模型的高阶频率差异较大。
减小中心体的转动惯量，即刚-柔投影惯量比减小，使得梁的高阶频率被激发出来，即使在较小的初始角下，系统也具有高阶频率(第三阶频率)，同样在较小的初始角下，也造成角速度波动变大，其峰值增加。在相同初始角下，刚柔投影惯量比较小的时候，3种模型的高阶频率差异较大。
系统的低阶频谱主要受中心刚体影响，与大范围运动关系不大。此外，可发现对于大范围运动为未知的刚-柔耦合柔性梁结构而言，新增耦合项对空间柔性梁结构影响较明显，而对于平面柔性梁结构并不显著。
3 结 论本文对大范围运动规律为未知的空间刚-柔耦合柔性梁建立了动力学方程，较零次模型和一次耦合模型，本文精确模型下动力学方程包含了完整的耦合项。
本文研究发现，在初始角度较大，即系统具有较大的运动速度和较大的大范围刚体运动时，零次模型与一次耦合模型和本文精确模型会出现差异，一次耦合模型和本文精确模型能够体现出动力刚化效应，其高阶频率会随着大范围运动的增加而上升，而零次模型则相反。对于空间刚-柔耦合结构，当大范围运动加剧后，本文精确模型下，系统的二阶以上频率低于一次模型，但仍高于零次模型，本文模型较一次耦合模型新增的耦合项，产生了“软化”作用。
本文计算结果表明，对于大范围运动为未知的刚柔耦合结构，其大范围运动的速度、幅度，依然是决定动力学特性和动力学模型适用的重要因素，在非惯性下的动力刚化效应，也存在于运动规律未知的刚-柔耦合结构中。
| [1] |
和兴锁,邓峰岩,王睿. 具有大范围运动和非线性变形的空间柔性梁的精确动力学建模[J]. 物理学报,2010,59(3):1428-1436 He Xingsuo, Deng Fengyan, Wang Rui. Exact Dynamic Modeling of a Spatial Flexible Beam with Large Overall Motion and Nonlinear Deformation[J]. Acta Physica Sinica, 2010, 59(3): 1428-1436 (in Chinese) |
| Cited By in Cnki (15) | Click to display the text | |
| [2] | Deng Fengyan, He Xingsuo. Dynamics Modeling for a Rigid-Flexible Coupling System with Nonlinear Deformation Field[J]. Multibody System Dynamics, 2007,18(4): 559-578 |
| Click to display the text | |
| [3] | Liu Yanzhu. On Dynamics of Elastic Rod Based on Exact Cosserat Model[J]. Chinese Physics B, 2009, 18(1): 1-8 |
| Click to display the text | |
| [4] |
孟宗, 刘彬. 一类非线性相对转动动力系统的平衡稳定性及组合谐波近似解[J]. 物理学报, 2008, 57(3): 1329-1334 Meng Zong, Liu Bin. Stability of Equilibrium State of a Kind of Nonlinear Relative Rotation Dynamic System and Associated Harmonic Approximate Solution[J]. Acta Physica Sinica, 2008, 57(3): 1329-1334 (in Chinese) |
| Cited By in Cnki (18) | Click to display the text | |
| [5] | Fu Jingli, Chen Benyong. Symplectic-Energy-First Integrators of Discrete Mechanico-Electrical Dynamical Systems[J]. Chinese Physics B, 2008, 17(11): 3942-3952 |
| Click to display the text | |
| [6] |
杨辉. 刚-柔耦合动力学系统的建模理论与实验研究[D]. 上海: 上海交通大学,2002 Yang Hui. Study on Dynamic Modeling Theory and Experiments for Rigid-Flexible Coupling Systems[D]. Shanghai, Shanghai Jiaotong University, 2002 (in Chinese) |
| Cited By in Cnki (39) | Click to display the text | |
| [7] |
刘锦阳. 刚-柔耦合动力学系统的建模理论研究[D]. 上海:上海交通大学,2000 Liu Jinyang. Study on Dynamics Modeling Theory of Rigid-Flexible Coupling Systems[D]. Shanghai, Shanghai Jiaotong University, 2000 (in Chinese) |
| Cited By in Cnki (84) | Click to display the text |
