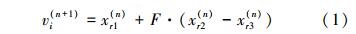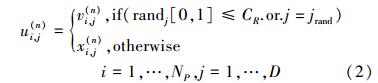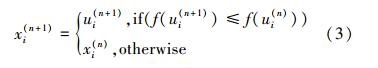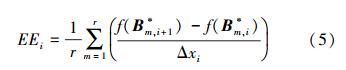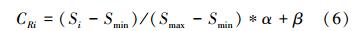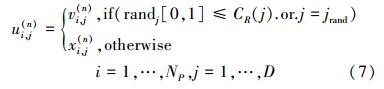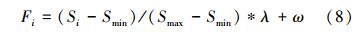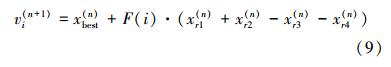微分进化算法(differential evolution,DE)与进化规划、遗传规划、遗传算法类似,都使用了优胜劣汰、适者生存的思想,是近年来发展的一种性能突出的进化算法(evolutionary algorithm)。DE由Rainer Stom 和 Kenneth Price于1995年提出[1],实践发现其收敛速度快、可调参数少、鲁棒性好、算法简单,在计算机、控制工程、化工、电力等众多学科中得到了广泛应用。国内外有许多学者进行过研究,苏海军、刘波、Swagatam Das等人[2, 3, 4]分别对DE算法研究进行了综述。
但是DE还存在一些问题,一方面是收敛性问题,DE也存在着早熟和局部搜索能力弱的缺点[5],而且在问题维度较高时更为严重,需要极高的计算量来保证优化效果;另一方面是如何针对特定问题设置合理的参数来保证良好的算法性能。为了继续提高DE的性能,有许多学者致力于对DE进行改进,一种思路是对已有操作算子进行改进,如Fan等人提出的三角法变异算子[6],另一种思路是提出新的操作算子,如Wang等提出的加速和迁移操作[7]研究。
本文针对以上两方面问题,提出将全局灵敏度分析方法(global sensitivity analysis,GSA)与DE相结合的改进思路。首先,计算灵敏度的过程就是从问题中提取更多信息的过程,用灵敏度信息来和优化算法结合,有助于算法捕捉问题的特征,从而提高算法性能。其次,通过构造新的算子公式,使用灵敏度信息对算法参数进行控制,一定程度上解决了算法参数设置的问题。
1 基本微分进化算法DE的变异、交叉、选择3种算子是算法的核心操作,下面予以简要介绍。设种群大小为NP,D为变量的维数,第n代种群为{x1(n),x2(n),…xi(n)…,xNP(n)},第n代种群中的第i个个体可表示为xi(n)=(xi,1(n),xi,2(n),…,xi,D(n))。
1.1 变异算子 在DE中,变异个体的生成过程使用到了父代种群中多个个体的线性组合。微分进化算法使用如下公式产生变异个体vi(n+1)xr1(n) 、xr2(n)、xr3(n)是从父代种群中按特定规则选择的3个不同个体,这里有一个暗含的要求是种群大小需要大于4,否则这里的随机性就无法保证了。F是一个常数,称为放缩因子,用来控制变异的比例。在种群进化过程中,如果已经靠近最优解,那么个体之间的差分值会逐渐减小,那么这种扰动就会自动变小。
放缩因子F较小会使得算法变异能力不足、对优化空间的探索能力不足,从而导致容易陷入局部最优;较大的F提高了算法搜索到全局最优的概率,但是当F较大时,算法的收敛速度会明显降低,这是因为当差分向量乘以F后会使变异个体距离父代较远,对父代个体的继承性较差,收敛速度会明显下降。根据一些学者针对测试函数的使用经验,放缩因子的选取范围为0.5~0.9。
Price和Storn对基本DE的变异公式进行微调,提出了几种不同的变异操作算子,具体细节的不同可用符号DE/X/Y/Z来区分。Price曾提出DE/BEST/2/BIN是一种比较值得研究的算子,本文采用这种算子作为基础进行改进。
1.2 交叉算子交叉运算的目的是通过变异个体和第n代个体的随机重组提高种群的多样性。标准微分进化算法的交叉公式如下
式中,ui(n)=(ui,1(n),ui,2(n),…ui,D(n))为交叉后产生的个体,randj是[0, 1]之间的随机数;CR是[0, 1]之间的一个常数,在优化运行开始前给定,称为交叉常量。CR的取值越大,发生交叉的概率越大,CR=0则没有交叉的可能。jrand是在r之间随机取值的一个整数随机变量,保证了ui,j(n)至少有一个分量是从vi,j(n)中获取,以确保有新的个体生成,通过这种手段来保持群体的活跃性,维持进化不断进行。
1.3 选择算子DE的选择操作是一对一贪婪选择,当测试个体ui(n)的适应度值比xi(n)的适应度值更好时,ui(n)会被接受成为下一代种群的一员;反之,xi(n)则会被保留。假设待求优化问题为求最小值,则选择操作如下所示
式中,f(xi(n))为xi(n)的适应值。
2 MOAT全局灵敏度分析方法 2.1 灵敏度分析方法灵敏度分析方法的主要研究内容是:定性或定量地分析输入变量(或参数)的变化如何影响输出值,简单说来就是分析输入参数对输出值影响的程度大小[8]。灵敏度分析的对象可以是任意一个系统或模型,只需要输入和输出数据即可,本质上是通过系统的数学性质对系统的内在特性进行研究。灵敏度分析方法有很多种,各种方法出于不同的目的而使用了不同的构造思想和数学工具,导致这些方法各具特色。对特定的问题而言,可根据其适用条件和使用要求选取最合适的方法。
灵敏度分析方法大体上可分为局部灵敏度分析方法、全局灵敏度分析方法和基于人工神经网络的方法这几大类[9]。局部灵敏度分析方法把导数信息、梯度作为灵敏度信息,这种信息是局限于某个基准点附近的信息,包括手工求导、有限差分、自动微分、复变量方法等几种。全局灵敏度分析方法是在整个定义域内,研究设计变量对系统输出的影响,又分为筛选法、蒙特卡罗方法、基于方差的方法等几类。筛选法通常用来处理含有大量输入变量的模型,包括OAT方法、COTTER方法、IFFD方法等,计算量相对比较小,MOAT[10]是其中较优秀的一种。蒙特卡罗方法包括散点图法、相关系数法、回归分析法,大多是使用统计学的方法,对于非线性、非单调的问题适用性较差。方差法包括重要性估计法、傅里叶幅值灵敏度测试法(FAST)等,是近年来研究发展最为迅速、应用最为广泛的一类方法。其中比较特殊的是Sobol方法[11],具有蒙特卡罗方法和方差法两方面的特点。关于这些方法的性能对比和分析,在若干文献[12]里面都可以找到其他学者的研究结果。灵敏度分析已广泛应用于大气化学、气体排放、鱼群动力学、综合指标分析、金融投资、放射性废物处理、地质信息系统、固体物理学等等方向。
近年来全局灵敏度分析方法的发展和应用远远超过了局部灵敏度分析方法,而基于神经网络的方法较新但研究较少。其中MOAT、Sobol等几种方法的研究最为广泛,MOAT方法的特点是适用于较高维度问题,计算量远远低于Sobol,但精度稍低于Sobol方法。
2.2 MOAT灵敏度分析方法Morris于1991年提出了一种One-at-a-time(OAT)方法,以下简称为MOAT方法,在GSA中是一种相对高效的方法。OAT方法的最主要特点是每次分析一个分量对输出的影响,如果需要分析所有分量的影响,那么需要多次计算。MOAT实际上是对各种局部灵敏度分析方法的拓展,主要是在可行域内随机取值,从而在一定程度上消除了对初始点的依赖,最后通过取平均值体现了全局性。MOAT方法可以用于识别具有多个输入变量的模型中的少数关键变量,一些学者把有这种作用的方法称为筛选法。
MOAT首先定义了Elementary Effect(EE),例如对于设计变量的第i个分量
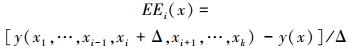
EE的定义式类似于偏导数,但是由于Δ的取值并非接近于无穷小,因此EE不同于偏导数。MOAT方法中,求解EE时的基准点x可在整个定义域内随机选取,因此在一定程度上摆脱了对于x的依赖。假设设计变量x=[x1,x2,…xk],共有k个分量。如果计算所有分量的影响,那么至少需要取k+1个点x1,x2…xk+1,最简单情况就是xi+1-xi=Δ·ei,ei=[0,0…1…0]是第i个分量为1的单位向量,Δ是MOAT方法选取的一个参数。
那么计算k+1个函数值,两两相减然后除以Δ就可求得k个EE。Δ是影响EE的一个重要参数。MOAT把设计变量的定义域离散化来求得Δ。例如分量xi的初始定义域是实数域,而现在使用MOAT只从{0,1/(p-1),2/(p-1),…,1}这p个值中随机选取某一个作为xi。这样一来,整个k维的定义域空间Ω被划分成k×p个网格点,x只能从这些网格点中随机选取。Δ为1/(p-1)的倍数。而且需要保证,当x为区域Ω中的任意值,点x+Δ仍在Ω内。MOAT的总计算量为r(k+1),每k+1个点组成一个路径(path),重复r次然后取平均即得到灵敏度。
MOAT方法的具体计算步骤如下:
实际使用中需要考虑基准点在定义域内的随机选取。随机化处理的步骤如下:
1) 令D*是k维对角矩阵,对角元素是1或者-1,概率各是0.5。设Jm,k是m×k的全1矩阵,得到(1/2)[(2B-Jm,k)D*+Jm,k]。
2) 设x*是随机选择的基准值,每一个分量都是从{0,1/(p-1),2/(p-1),…,1-Δ}中随机等概率地选择一个值。
3) 设P*是一个k维随机扰动矩阵,每一列包含一个1,其他所有元素都是0,而且任意2列的1不在同一行。
其中D*、x*、P*是各自独立地随机生成。最后就得到了
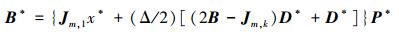
B*实质上就是前述矩阵B的随机形式。如果重复r次,就得到了[B1* B2* …Br*]T。计算时,对r次的结果进行平均,这就是MOAT定义的灵敏度信息。
式中,f(Bm,i*)是第m个B*的第i行。
2.3 MOAT方法与Sobol方法对比分析本小节对MOAT与Sobol 2种方法进行对比,使用这2种方法对测试函数进行灵敏度计算并对比二者在计算效率、计算精度方面的问题。由于MOAT方法和Sobol方法的原理不同,这2种方法使用了2种不同的数学方式来度量灵敏度信息。但是Campolongo发现,MOAT方法定义的Elementary Effects可以作为对Sobol方法定义的Sti(total sensitivity indice)一个较好的近似,理想情况下二者会逼近于同样一个期望,因此具有一定的可比性[13]。
此处给出的是Sobol gstar function的测试结果对比,这个函数是Sobol和很多学者在灵敏度研究时经常使用的测试函数中的一个。gstar函数中的系数采用a=[0,0.1,0.2,0.3,0.4,0.8,1,2,3,4]。
由于MOAT和Sobol方法都依赖于样本进行计算,因此样本数量的影响十分重要。在具体操作过程中,应逐渐提高样本数量直至计算收敛,结果才是可信的。MOAT设置参数为:level=4,重复10次,总计110个样本。Sobol方法使用拉丁超立方取样,样本总数1 200个。计算结果如图 1~图 2所示,横坐标是设计变量的序号,纵坐标分别是MOAT和Sobol定义的灵敏度值。
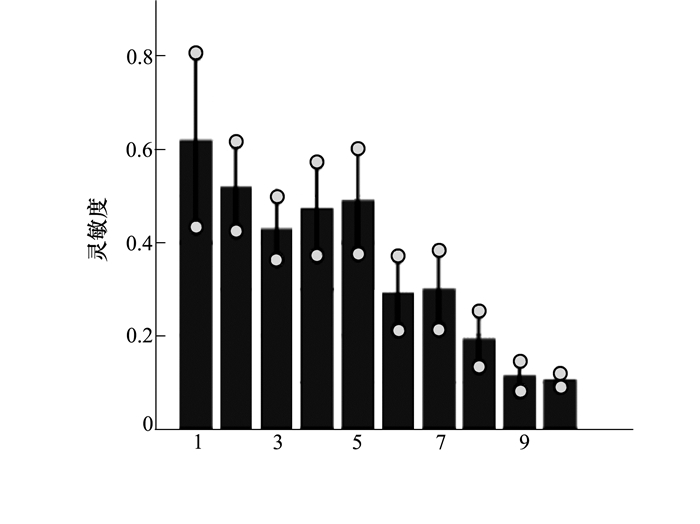 |
| 图 1 gstar函数使用MOAT计算灵敏度结果 |
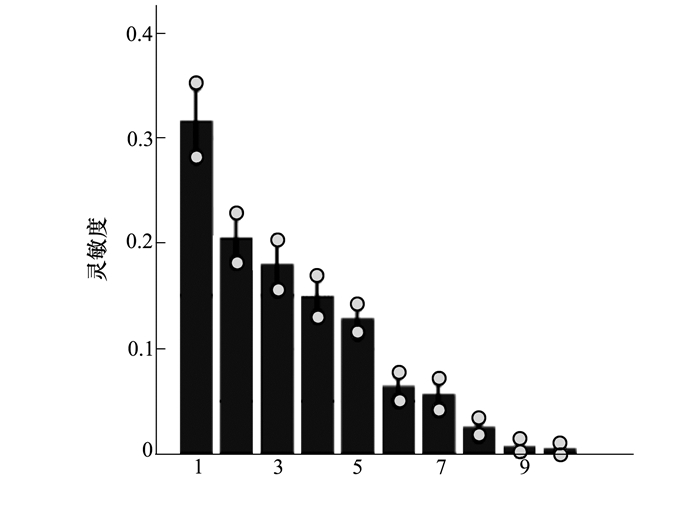 |
| 图 2 gstar函数使用Sobol计算灵敏度结果 |
从这2种方法的计算结果可以看出,MOAT的Elementary Effects和Sobol的Total Sensitivity Indice有近似相同的趋势,但是具体数值有所差异。g函数的结果中对x2和x4的灵敏度计算差别较大。gstar函数的结果MOAT不如Sobol的结果精确。从参数设置来看,x1至x10的权重系数依次递减,那么灵敏度应该也是依次递减的,Sobol正确体现出了这种趋势。MOAT由于样本生成方法的影响,在每个变量的区间中取定若干点,而不是完全随机取值,这样在灵敏度计算时,设计变量的每一维的取值比较固定。可能就是这种原因导致了MOAT的灵敏度精度比Sobol稍差一些。另外,图中显示的圆圈表示求解灵敏度方差。
测试算例表明:MOAT方法的理论基础弱于定量分析,但优点是需要样本数量少。Sobol方法理论较严密,但计算量需求极大。考虑到本研究的应用背景是针对计算量受到限制的问题,Sobol方法实用性不强,而且对于改进DE而言,对灵敏度的精度要求并非很高,因此选择MOAT方法来展开后续研究。
3 改进微分进化算法针对某些实际工程问题,需要在给定计算量约束的情况下,尽量获取更好的优化结果。这也就限制了种群的规模和迭代次数,对优化算法的性能提出了更苛刻的要求。
本文研究提出了2种改进思路,分别对微分进化算法的交叉和变异公式进行修改,主要考虑灵敏度信息是对设计变量的重要程度的一种度量,灵敏度值越大,表明对输出的影响越大,那么在算法迭代过程中,可以考虑将灵敏度信息耦合到变异算子或者交叉算子中去。本质上,这是通过灵敏度信息来控制交叉或者变异算子,其思路与自适应DE的一些方法类似。
第一种改进方式是修改交叉算子,改进后的DE以下简称为GSADE1。根据灵敏度计算的结果,可以据此修改每个分量的交叉概率。具体操作方式为:将CR扩展为矢量,CR=[CR1,…CRD],其维度和设计变量的维度相同,CR的每个分量的大小使用灵敏度信息来控制。设灵敏度矢量S=[S1,…,Si,…SD],其中灵敏度的最小值和最大值分别是Smin=min(S)、Smax=max(S),那么可以得到CR的计算公式如下
式中,α和β相加等于1,例如α=0.4、β=0.6,另外假设灵敏度的值是大于零的,那么CRi最终是在[0.6,1]之间变化,即式中的Si首先被归一化,然后被缩放到指定的区间内。最后,微分进化算法的交叉公式如下,基本形式保持不变。考虑到MOAT方法计算的精度不是很高的问题,通过设置参数能保证交叉算子的值位于一定区间内,即使灵敏度精度不足,也能保证一定量的交叉概率,减弱了因灵敏度计算精度不足的影响。改进变异算子的思路也是同理。
第二种改进方式是修改变异算子,改进后的DE以下简称为GSADE2。本文使用的变异算子形式如下,从中可以看出主要影响因素就是个体的选取和放缩因子F的影响。对F的修改方式与CR类似,将F扩展为矢量,F=[F1,…FD],其维度和设计变量的维度相同,F的每个分量的大小使用灵敏度信息来控制。设灵敏度矢量S=[S1,…,Si,…SD],其中灵敏度的最小值和最大值分别是Smin/sub>=min(S)、Smax=max(S),那么可以得到F的计算公式如下
例如λ=0.3、ω=0.7,另外优于灵敏度的值是大于零的,那么Fi最终是在[0.7,1]之间变化,即式中的Si被变换到指定的区间内。最终得到改进后的变异公式如下
4 函数测试及分析本节使用5个解析函数作为测试问题,采用基本DE和改进算法分别寻优,以验证改进算法的性能。使用2005年IEEE进化计算大会的标准测试函数[14]中的中的Shifted Schwefel′s、Shifted Rotated High Conditioned Elliptic Function、Shifted Rosenbrock′s Function、Shifted Rotated Rastrigin′s Function、Shifted Rotated Expanded Scaffer′s,仿照该文献中的编号依次称为函数2、3、6、10、14,设计变量范围和函数中的参数均使用文献中所给出的值。其中,函数2是单峰值函数,函数3是高条件数的单峰值函数,函数6是多峰值函数,函数10和函数14具有旋转性和极多局部峰值。这几个函数包含了单峰值、多峰值、带旋转等多种特性,因此具有一定的代表性。这几个函数的维度可以人为指定,考虑到本文面向的工程问题的维度在50维左右,因此针对50维的情况来进行测试。
各函数均使用MOAT方法计算灵敏度信息,样本总数510个,如果收敛较快则减少样本数目。
初始DE参数设置使用DE/BEST/2/BIN变异算子,放缩因子F=0.5,交叉因子CR=0.9。GSADE1参数设置是α=0.1、β=0.9、放缩因子F=0.5。GSADE2参数设置是λ=0.2、ω=0.5、交叉因子CR=0.9。除了以上区别,改进算法的其他参数都与初始DE相同。种群大小统一设定为50和100,限定进化50代。
对每个函数重复测试20次,将收敛历史求和取平均,得到平均的收敛历史。收敛的最终结果的20次平均值如表 1所示。
| 标准测试函数 | 种群50收敛平均值 | 种群100收敛平均值 | ||||
| 初始 | 改进1 | 改进2 | 初始 | 改进1 | 改进2 | |
| F2 | 1 188.65 | 369.95 | 1 124.80 | 390.03 | -235.48 | -194.02 |
| F3 | 2 560.44 | 2 895.55 | 5 955.27 | 3 362.55 | 2 126.04 | 2 852.10 |
| F6 | 478.27 | 390.85 | 444.53 | 422.99 | 393.57 | 411.60 |
| F10 | -328.41 | -327.59 | -328.73 | -329.53 | -329.62 | -329.69 |
| F14 | -294.21 | -294.66 | -295.90 | -295.95 | -297.13 | -297.58 |
图 3~图 7显示了3个较复杂测试函数的最后20步平均收敛曲线。
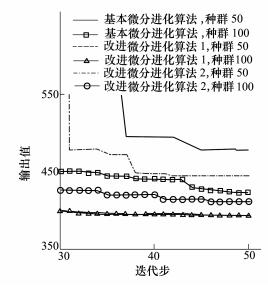 |
| 图 3 函数6收敛结果 |
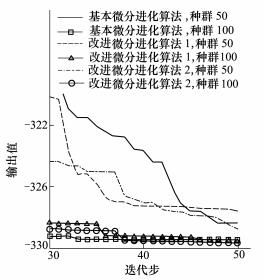 |
| 图 4 函数10收敛结果 |
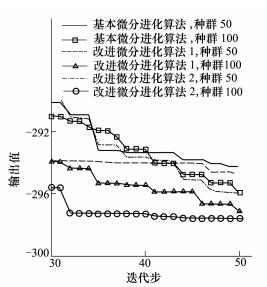 |
| 图 5 函数14收敛结果 |
种群数100的优化结果显示:2种改进算法完全优于初始DE。考虑到计算灵敏度信息使用的样本数量,GSADE1和GSADE2的收敛速度也比基本DE更快。在函数2、函数6、函数14中改进算法优势明显。而在函数3、函数10算例中,改进算法在优化前期优势不明显,但是在算法后期优于DE,最终GSADE1和GSADE2的收敛结果都优于DE。
在种群数50的情况下,GSADE1只在函数2、函数6、函数14的测试中优于DE。主要原因可能是在种群50严重不足地情况下,由于灵敏度对交叉概率的影响,导致在函数3、函数10的测试中后期开发能力弱化。虽然在早期搜索中收敛较快,但是在算法后期开发能力不足。GSADE2优于GSADE1,只有函数3的测试中表现差于DE。这个算例表明交叉算子和变异算子对开发能力的影响有所不同。
5 结 论本文提出2种基于全局灵敏度分析的改进DE算法GSADE1和GSADE2并进行了算例验证,得出以下结论:
1) MOAT方法计算效率高,精度稍低于Sobol方法,将之与优化算法结合对于改善优化搜索结果、提高优化效率具有积极作用。
2) 2种改进DE算法在种群数等于100的情况下完全优于初始DE,而在种群数50的情况下GSADE2优于GSADE1,但是仍有所不足,需要进一步针对极小种群的情况进行研究。
| [1] | Storn R, Price K. Differential Evolution-a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359 |
| Click to display the text | |
| [2] |
苏海军,杨煜普,王宇嘉. 微分进化算法的研究综述[J]. 系统工程与电子技术, 2008, 30(9): 1793-1797 Su Haijun, Yang Yupu, Wang Yujia. Research on Differential Evolution Algorithm: a Survey[J]. Systems Engineering and Electronic, 2008, 30(9): 1793-1797 (in Chinese) |
| Cited By in Cnki (79) | Click to display the text | |
| [3] |
刘波,王凌,金以慧. 差分进化算法研究进展[J]. 控制与决策, 2007, 22(7): 721-729 Liu Bo, Wang Ling, Jin Yihui. Advances in Differential Evolution[J]. Control and Decision, 2007, 22(7): 721-729 (in Chinese) |
| Cited By in Cnki (444) | Click to display the text | |
| [4] | Das S, Suganthan P N. Differential Evolution: a Survey of the State-of-the-Art[J]. IEEE Trans on Evolutionary Computation, 2011, 15(1): 4-31 |
| Click to display the text | |
| [5] |
赵光权. 基于贪婪策略的微分进化算法及其应用研究[D]. 哈尔滨:哈尔滨工业大学, 2007 Zhao Guangquan. Differential Evolution Algorithm with Greedy Strategy and Its Applications[D]. Harbin, Harbin Institute of Technology, 2007 (in Chinese) |
| Cited By in Cnki (18s) | |
| [6] | Fan H Y, Lampinen J. A Trigonometric Mutation Operation to Differential Evolution[J]. Journal of Global Optimization, 2003, 27(1): 105-129 |
| Click to display the text | |
| [7] | Wang F S, Jing C H, Tsao G T. Fuzzy-Decision-Making Problems of Fuel Ethanol Production Using a Genetically Engineered Yeast[J]. Industrial & Engineering Chemistry Research, 1998, 37(8): 3434-3443 |
| Click to display the text | |
| [8] | Saltelli A, Ratto M, Andres T, et al. Global Sensitivity Analysis[M]. The Primer, John Wiley and Sons, 2008 |
| [9] |
朱亚涛. 基于敏度分析的飞行器气动/隐身综合优化设计策略研究[D]. 上海:上海交通大学, 2010 Zhu Yatao. The Strategy Investigation on Aircraft Aerodynamic——Stealth Composite Optimal Design Based on Sensitivity Analysis[D]. Shanghai, Shanghai Jiaotong University, 2010 (in Chinese) |
| Cited By in Cnki (4) | |
| [10] | Morris M D. Factorial Sampling Plans for Preliminary Computational Experiments[J]. Technometrics, 1991, 33: 161-174 |
| Click to display the text | |
| [11] | Sobol' I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Mat Model, 1990, 2(1): 112-118 |
| Click to display the text | |
| [12] | Gan Y, Duan Q, Gong W, et al. A Comprehensive Evaluation of Various Sensitivity Analysis Methods: A Case Study with a Hydrological Model[J]. Environmental Modelling & Software, 2014, 51: 269-285 |
| Click to display the text | |
| [13] | Campolongo F, Cariboni J, Saltelli A. An Effective Screening Design for Sensitivity Analysis of Large Models[J]. Environmental Modelling & Software, 2007, 22(10): 1509-1518 |
| Click to display the text | |
| [14] | Suganthan P N, Hansen N, Liang J J, et al. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization[J]. Nanyang Technological University, 2005(1): 341-357 |
| Click to display the text |