随着对复杂产品设计提出的安全性指标要求,基于可靠性的多学科设计优化(reliability-based multidisciplinary design optimization,RBMDO)引起广泛关注[1]。概率模型是量化随机不确定性的常用方法,然而概率建模所需大量统计数据往往难以获得,需要采用分布未知、边界可知的区间不确定性模型。在实际工程问题的可靠性分析过程中,由于数据缺乏和认知不完全,需要同时考虑概率型和区间型不确定性因素。目前此类问题的研究主要集中在结构可靠性设计领域[2, 3],所发展的方法仅适用于单学科问题,用于多学科问题时效率很低,无法满足复杂的多学科耦合系统可靠性分析要求。
近年来,随机与区间不确定性下的多学科系统可靠性分析(multidisciplinary reliability analysis,MRA)问题引起了一些学者的关注。Guo等[4]将基于可靠度指标法(reliability index approach,RIA)的结构可靠性分析方法应用于多学科系统,提出序列双循环法(sequential double loops,SDL)、序列单循环法(sequential single loops,SSL)和序列单回路方法(sequential single-single loops,SSSL)。这些方法存在求解模型和求解流程2个方面的问题:在求解模型方面,由于采用RIA可靠性分析模型,难以求解复杂的极限状态函数,且过于依赖随机变量的概率分布类型,当可靠度接近于1.0时计算量巨大;在求解流程方面,SDL方法虽然将概率可靠性分析与区间可靠性分析序列化执行,但是直接在内部嵌套多学科分析(multi-disciplinary analysis,MDA)导致求解效率很低;SSL应用单学科可行(individual discipline feasible,IDF)方法,将MDA融入上层优化以减少迭代次数,但概率可靠度求解难度增加,收敛效率降低;SSSL方法结合SDL和SSL方法,在概率可靠性分析时采用MDF方法而区间可靠性分析采用IDF方法,以平衡求解效率和收敛难度之间的矛盾,但由于RIA模型本身的缺点,以及传统序列化方法在远离最优点的区域浪费太多计算资源,致使SSSL方法的效率和适应性仍然不高。
刘继红等[5]在Guo研究的基础上对其分析模型进行改进,将基于性能测度法(performance measurement approach,PMA)的可靠性分析模型应用于SDL方法中,提出了序列化集成改良的先进均值法(sequential modified advanced mean value,SMAMV)。该方法在计算效率上有所提高,然而其区间可靠性分析采用MDA与凸模型分析串联形式进行运算,在处理极限状态函数输入包含学科状态变量时存在很大的计算误差,且运用拉格朗日乘子法进行凸模型极值分析只在解析函数求解时具有较高效率。
面临随机与区间不确定性共存情况下的多学科可靠性分析问题,迫切需要发展能保证求解精度同时又提高计算效率和适应性的方法。
本文在Guo等提出的SSSL求解框架的基础上,综合采用以下措施,提出了一种改进方法:
1) 为了提高求解流程的效率,在2个问题迭代时采用宽容分层思想,在求解概率可靠性问题时,不是在迭代过程每次收敛到最优值,而是分阶段地采用先进均值法[6](advanced mean value,AMV)、圆弧搜索法[7](arc search)和有效集拟牛顿法[8](active set Quasi-Newton algorithm,ASNA),形成了一种渐进的迭代模式,以减少搜索初期大量迭代分析,同时降低搜索初期陷入局部最优解的风险。
2) 为了提高可靠性分析模型本身的效率和适应性,采用PMA概率可靠性分析模型与区间极值分析模型相结合,形成新的混合变量可靠性分析模型[9, 10]。
3) 为了提高求解多学科问题的效率,概率多学科可靠性分析时,将MDA从循环中剥离,以区间极值分析所得到的状态变量作为MPP搜索时求解全局敏度方程的输入,以提高求解效率。
通过采用以上措施,以提高多学科可靠性分析的计算效率和适应性。
1 基于PMA的MRA模型当可靠性问题的变量同时包含随机和区间不确定性时,其功能函数可表示为

处理可靠性分析可以采用RIA或PMA模型。RIA是给定极限状态值以计算约束函数大于或小于极限状态值的概率(可靠度);PMA则是基于可靠性反问题策略而提出的,是给定失效概率以计算特定的约束函数极限状态值。 对包含N个学科的多学科系统,PMA模型可表示为:
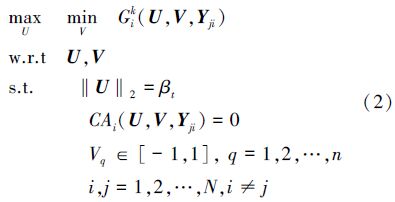
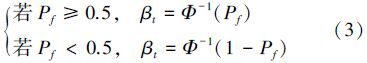
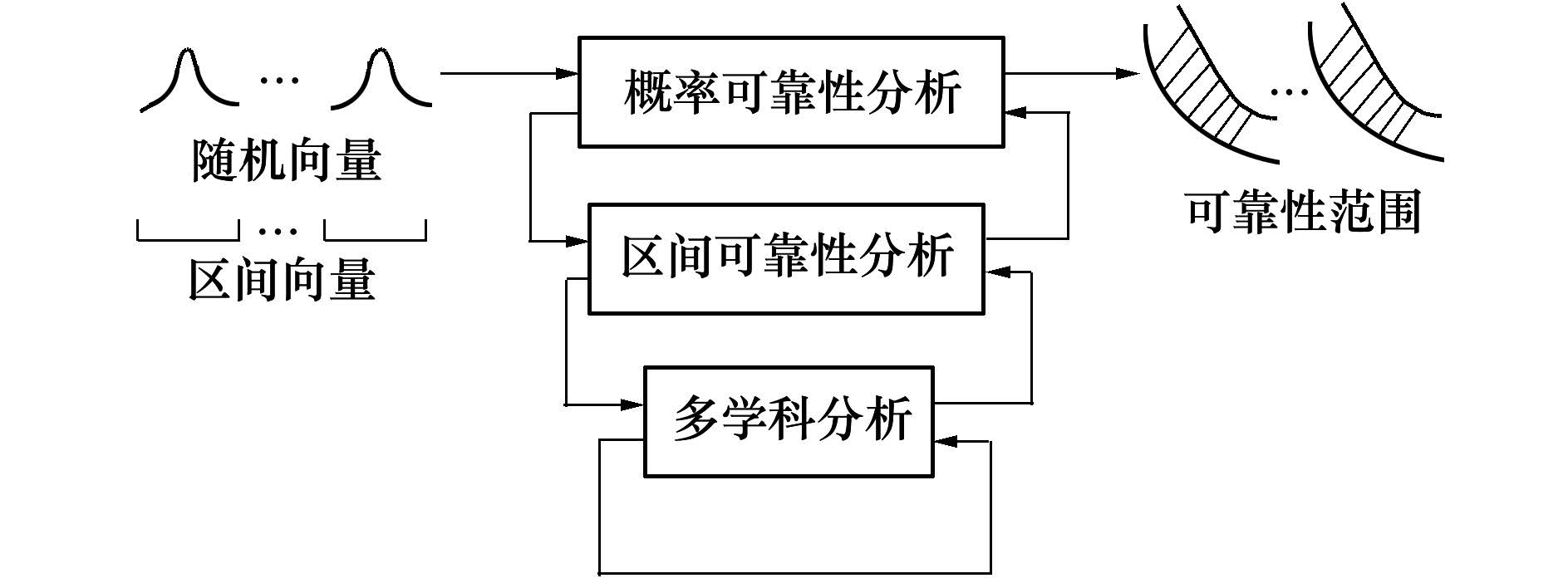
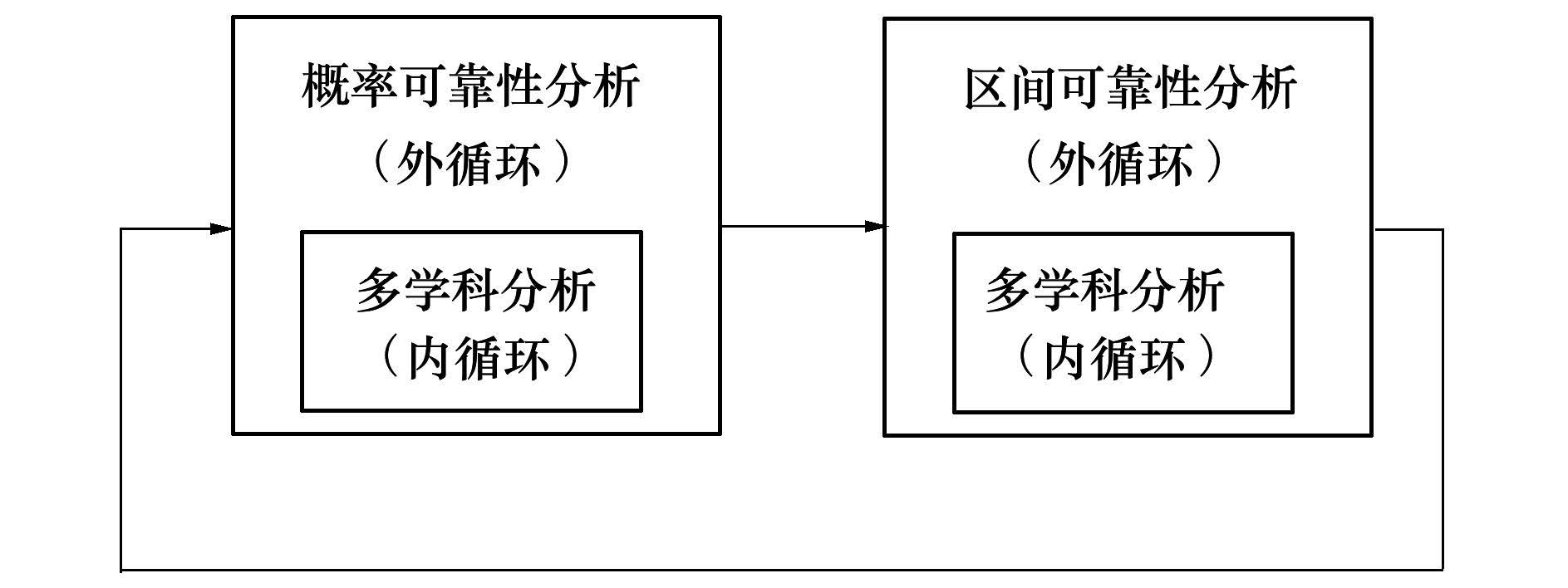
当同时考虑随机与区间不确定性时,为了合理利用不确定信息,需要将2种不确定性分开处理,此时的MRA不仅要进行MDA和概率可靠性分析,还需要进行多学科区间可靠性分析。现有的混合不确定性条件下的MRA方法主要有嵌套方法(见图 1)和序列化方法(见图 2)。
|
| 图 1 三层嵌套MRA |
|
| 图 2 传统序列化MRA |
嵌套方法的MDA处在最内层,学科分析次数异常庞大,处理高拟真度学科模型存在很大困难;序列化方法进行在一部分变量固定的前提下优化另一部分变量,搜索初期在远离最优点的区域浪费大量计算资源,且容易陷入局部最优点。
针对嵌套方法与传统序列化方法所具有的求解困难和学科平衡困难,本文综合2类方法的优点,提出宽容分层序列化多学科可靠性分析方法(stratified sequencing multi-disciplinary reliability analysis method,SSMRAM)。
2.1 基本原理分层序列法是将问题中多个目标函数按重要程度排序,以此序列求出各个目标的最优解,后一个目标在前一个目标的最优阶级内进行优化的。其应用于混合不确定性MRA时,先固定V=V*值求解:
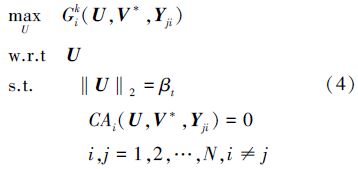
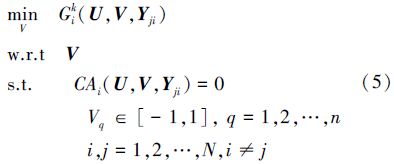
然而该方法存在优化早熟的问题,因此引入宽容的思想,即在求解后一个目标函数的最优解时,对前一个目标不求得严格最优解,而是在前一个目标最优值附近一定范围内进行优化。
本文在进行可靠性分析时,对极限状态函数的负梯度向量-$\nabla $Ug与随机向量u的夹角γk引入宽容值κ,将原来的收敛准则γk≤ε改为γk≤ε+κ,具有一定的宽容度。当γk>ε+κ时,采用AMV方法单步更新随机变量向量U,见(6)式,其中Vk由(5)式求解
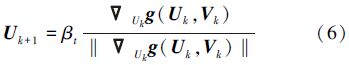
当γk≤ε+κ采用圆弧搜索方法求解逆MPP点,见(7)式,其中Vk由(5)式求解。
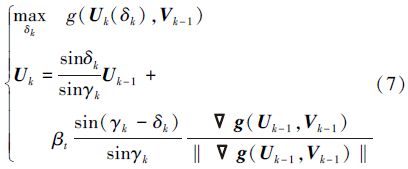
本文采用AMV和圆弧搜索方法在进行概率可靠性分析时搜索逆MPP点,采用ASNA方法进行区间极值分析。
1)AMV方法是一种运算简单,易于实现的逆MPP点搜索算法,如图 3所示,其原理是将标准正态向量指向极限状态函数的梯度方向,采用以下迭代格式
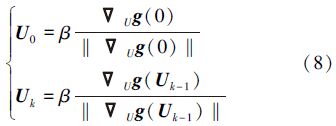
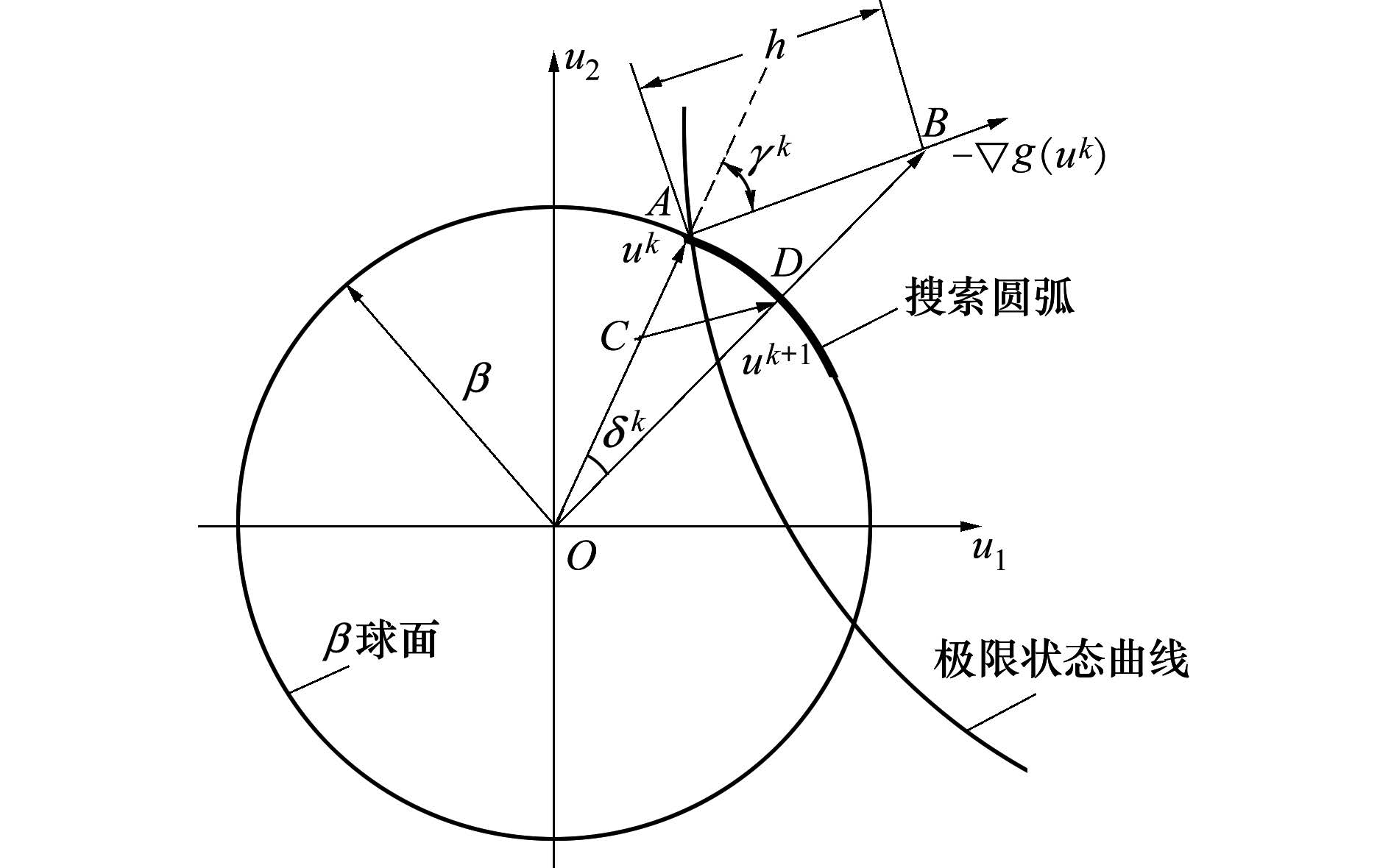
|
| 图 3 逆MPP点求解示意图 |
该方法在处理图极限状态函数时具有较好的效率,处理非凸函数效率不高。
2)圆弧搜索算法是将原来搜索逆MPP点问题中的等式约束‖U‖2=βt,通过几何运算引入Uk中,计算模型如下
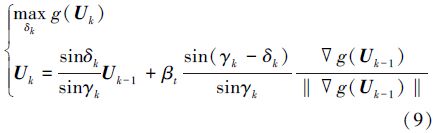
3)ASNA方法是一种求解序列二次规划问题的算法,它将有效集进一步划分为满足KKT条件和违反KKT条件两部分,使其具有全局收敛性质,对初值不敏感,具有很好的适应性。其在求解初值不在可行域内的区间极值分析问题具有良好的求解效率和收敛特性。
2.3 SSMRAM求解步骤本文所提SSMRAM方法的求解流程如图 4所示,具体步骤如下:
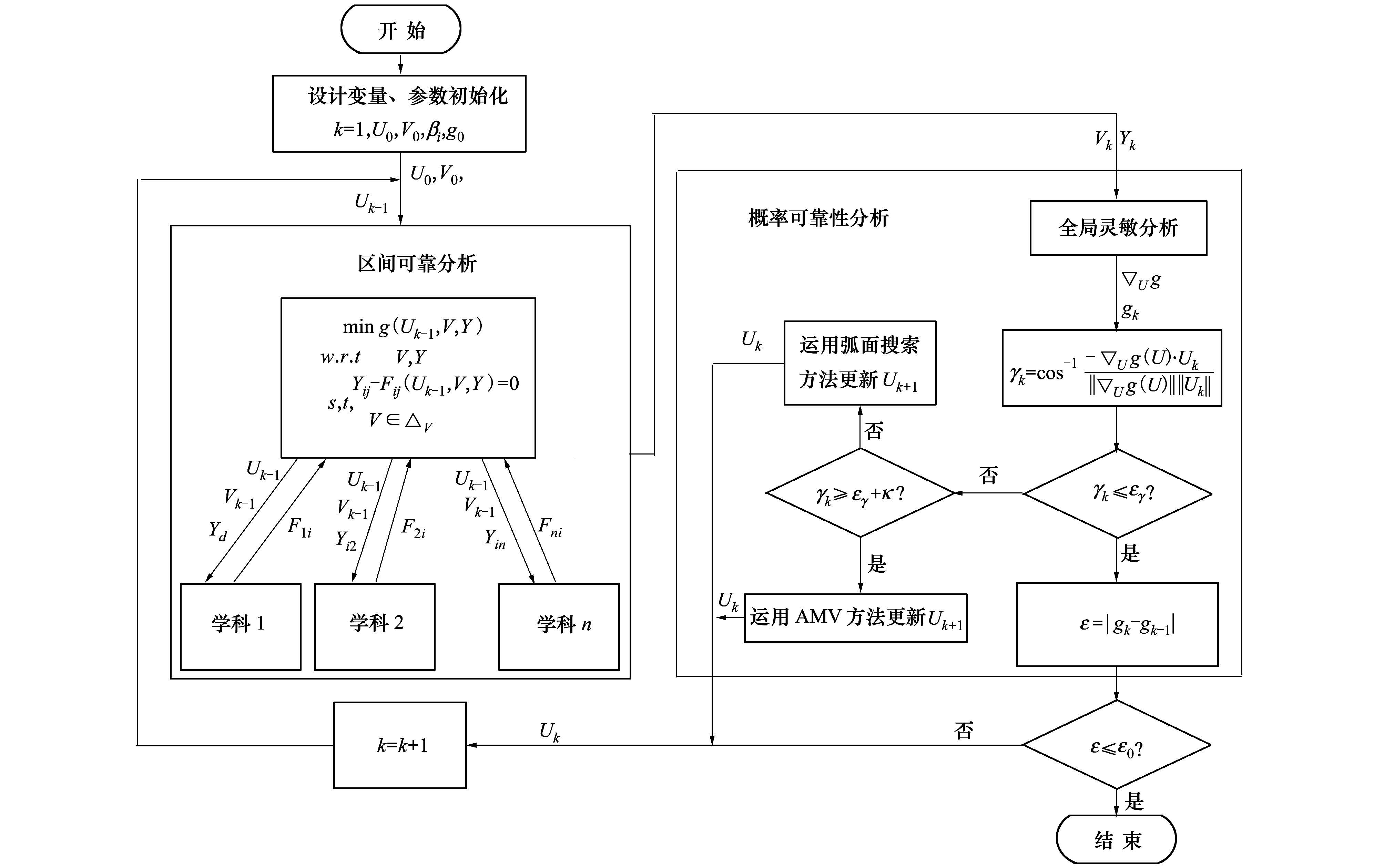
|
| 图 4 随机与区间不确定性下的分层序列化的MRA混合算法流程 |
步骤1 将随机变量转换到标准u空间,将区间变量标准化。
步骤2 设置初始值:k=1,U0,V0,βt,g0,εγ,ε0,κ=1。
步骤3 令U=Uk-1,运用ASNA求解具有系统一致性约束的区间可靠性极值问题,求出极小值gk对应的Vk,Yk。
步骤4 令V=Vk,Y=Yk,执行系统灵敏度分析,将g看作系统状态变量,利用全局灵敏度方程获得$\nabla $Xg(Xk),再由(10)式求出极限状态函数在标准正态空间中的梯度$\nabla $Ug(Uk)。
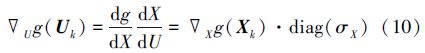
步骤5 以(11)式计算-$\nabla $Ug(U)与Uk之间的夹角γk。
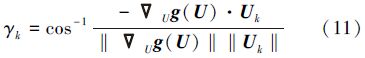
步骤6 判断γk≤εγ?若是,则转步骤7;若否,转步骤8。
步骤7 判断|gk-gk-1|≤ε0?,若是,则转步骤10;若否,则Uk=Uk-1转步骤9。
步骤8 判断γk≥εγ+κ?若是,则运用AMV更新Uk,如(6)式所示;若否,则运用圆弧搜索方法更新Uk,如(7)式所示。
步骤9 令k=k+1,转步骤3。
步骤10 UMPP=Uk,Vmin=Vk,结束。
2.4 SSMRAM特点本文所提的SSMRAM具有以下特点:
1) 采用的PMA模型求解效率更高、适应性更强,从可靠性分析模型本身提高多学科的概率可靠性分析的效率。
2) 采用IDF方法将原来由区间可靠性分析和MDA组成的2层循环转化为单层二次规划问题,并采用学科分析并行执行,提高了计算效率;并采用ASNA求解该问题。ASNA将有效集进一步划分为满足KKT条件和违反KKT条件两部分,可降低对初值的敏感度,具有很好的收敛特性。
3) 区间可靠性分析所得结果满足系统一致性约束,其设计变量和状态量可以直接用于全局灵敏度分析,为搜索MPP省去了MDA过程,提高了效率。
4) 搜索初期以宽容分层序列法的思想,不搜索精确MPP点,只运用AMV方法进行单步更新,以快速确定搜索方向,搜索后期迭代采用圆弧搜索方法以加快收敛速度。
3 算例验证通过以下2个算例对SSMRAM做如下验证:以算例1验证其求解精度和计算效率;以算例2验证其在实际工程问题中的有效性和适应性。
3.1 测试算例1:解析函数算例1包含2个子系统和3个设计变量,子系统1包含x1,x2和x3,子系统2包含x1和x3。其中,x1和x3是共享设计变量,x1和x2为服从正态分布的随机设计变量,x3为区间设计变量;g1和g2分别为各子系统的约束。2个子系统的输入输出关系如(13)式和(14)式所示。

学科1:
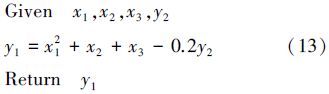
学科2:
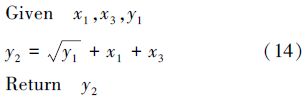
选取2个试验点:
1) 试验点1: U=(x1,x2)~N(μx,σx)为随机设计变量,其中μx=(-2.2,0.1),σx=(0.2,0.1);V=x3∈[0.1,0.2]为区间设计变量。给定失效概率Pf=1.5%,换算为可靠度指标βt=2.170 1。
2) 试验点2:U=(x1,x2)~N(μx,σx)为随机设计变量,其中μx=(-1.5,0.1),σx=(0.1,0.1);V=x3∈[0.1,0.2]为区间设计变量。给定失效概率Pf=99%,换算为可靠度指标βt=2.326 3。
对极限状态函数g1进行可靠性分析。对试验点1和试验点2分别采用本文所提方法,蒙特卡罗方法、SDL方法、SSL方法、SSSL方法和SMAMV方法进行可靠性分析。计算MPP点坐标,极限状态函数值,迭代次数和学科函数分析次数如表 1所示。
| 分析方法 | xMPP=(x1,x2,x3) | 极限状态函数 | 迭代次数 | 学科函数分析次数 | ||
| 学科1 | 学科2 | |||||
| SDL | 1 | (-1.769 8,0.071 2,0.100 0) | g1min=0.036 5 | 3 | 585 | 585 |
| 2 | (-1.724 4,0.161 5,0.100 0) | g1min=0.013 3 | 3 | 1 257 | 1 257 | |
| SSL | 1 | (-1.769 8,0.071 2,0.100 0) | g1min=0.036 5 | 3 | 432 | 432 |
| 2 | (-1.724 4,0.161 5,0.100 0) | g1min=0.013 3 | 3 | 480 | 480 | |
| SSSL-AMV | 1 | (-1.769 8,0.071 2,0.100 0) | g1min=0.036 5 | 4 | 488 | 488 |
| 2 | (-1.724 3,0.161 5,0.100 0) | g1min=0.013 3 | 5 | 561 | 561 | |
| SMAMV | 1 | (-1.769 8,0.071 2,0.200 0) | g1min=0.060 5 | 4 | 452 | 452 |
| 2 | (-1.724 3,0.161 6,0.200 0) | g1min=0.037 2 | 3 | 410 | 410 | |
| 本文方法 | 1 | (-1.769 8,0.071 2,0.100 0) | g1min=0.036 5 | 4 | 200 | 200 |
| 2 | (-1.724 4,0.161 5,0.100 0) | g1min=0.013 3 | 4 | 249 | 249 | |
| 蒙特卡罗 | 1 | (-1.770 1,0.070 3,0.104 3) | g1min=0.037 6 | 500 000 | 7 590 000 | 7 590 000 |
| 2 | (-1.724 5,0.161 1,0.100 9) | g1min=0.013 5 | 500 000 | 6 300 000 | 6 300 000 | |
由表 1各方法的计算结果可知,除SMAMV方法外,与蒙特卡罗法所得结果差距甚微,说明SSMRAM方法计算精度值得信任。在相同收敛精度条件下,SSMRAM方法所需分析次数远小于蒙特卡罗法、SDL、SSL、SSSL方法,对学科函数的分析次数减少47%以上,因此在分析多学科可靠性时具有更高的效率。
3.2 测试算例2:航空飞行器本算例为航空飞行器总体参数优化问题[11]。考虑气动、质量、性能3个学科的相互影响,以飞行器总质量最小为优化目标,并满足失速速度和航程的约束要求。其极限状态函数如(15)式所示,3个学科的输入输出关系分别如(16)~(18)式所示。
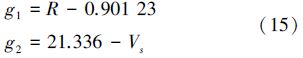
气动学科:
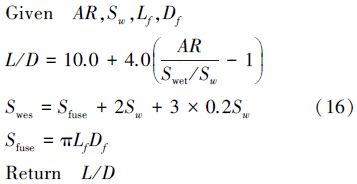
质量学科:
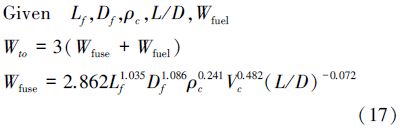
性能学科:
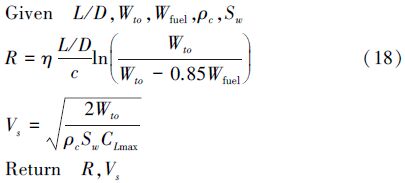
为了验证本文所述方法在飞行器这类多变量、多耦合的多学科系统中进行可靠性分析的有效性、计算效率和收敛特性,对上述算例的设计变量改造如下:
1) 试验点1:随机设计变量U=(AR,Lf,Df,ρc)~N(μU,σU),μU=(8.52,5.85,1.01,0.92),σU=(0.15,0.02,0.01,0.05),区间设计变量V=(Sw,Vc,Wfuel)∈[aV,bV],aV=(27.50,59.16,150.00),bV=(27.87,60.96,156.00)。
2) 试验点2:随机设计变量U=(AR,Lf,Df)~N(μU,σU),μU=(9.11,6.19,1.22),σU=(0.10,0.01,0.01)。区间设计变量V=(ρc,Sw,Vc,Wfuel)∈[aV,bV],aV=(0.95,26.87,59.96,152.08),bV=(0.98,27.85,60.16,155.98)。
给定失效概率Pf=0.13%,换算为可靠度指标βt=3.0。分别对极限状态函数g1和g2进行多学科可靠性分析,获得MPP点、极限状态函数值、迭代次数、学科分析次数和约束函数g评价次数如表 2和表 3所示。
| 试验点 | MPP点坐标 | g1min | 迭代次数 | 学科分析次数 | g1评价次数 |
| 1 | (8.466,5.860,1.039,0.948,27.500,60.960,150.000) | 0.071 2 | 4 | 416 | 289 |
| 2 | (9.074,6.196,1.249,0.980,26.870,60.160,152.000) | -0.035 0 | 3 | 410 | 315 |
| 试验点 | MPP点坐标 | g2min | 迭代次数 | 学科分析次数 | g2评价次数 |
| 1 | (8.519,5.853,1.020,0.779,27.500,60.960,156.000) | 14.155 2 | 4 | 406 | 251 |
| 2 | (9.108,6.196,1.250,0.950,26.870,60.160,155.980) | 14.285 8 | 3 | 300 | 205 |
由表 2和表 3可以看出,在随机变量和区间变量个数发生变化、试验点不同的情况下,本文所述方法对试验点1和试验点2均可以正常求解,说明本文所述方法是有效可行的;对于含有7个设计变量、3个子系统的多学科系统求解仅需迭代3~4步,收敛特性良好;与表 1中所示3个设计变量、2个子系统的多学科问题的学科分析次数增长不到2倍,说明本文所提方法在处理多变量多学科问题时具有较好的求解效率。
另外,为了验证本文所提方法求解的鲁棒性,随机产生100个初值(取值范围为[-1 000,1 000])对试验点1和试验点2进行可靠性分析,求解成功率均为100%,且平均迭代次数为5.78次,说明本文所述方法具有很好的鲁棒性,对初值不敏感,进而证明了本文所提分层序列化方法在初始搜索阶段具有较高搜索效率。
上述3个算例及其计算结果可以看出:
1)在方法可行性方面,算例1和算例2中可靠性分析问题的成功求解,说明在随机不确定性和区间不确定性共存情况下,本文所述方法在进行可靠性分析是有效可行的。
2)在求解效率方面,算例1中对各种现有的可靠性分析方法与本文所述方法进行了比较,证明本文方法在满足求解精度的同时,学科分析次数少50%以上,具有更高的求解效率;3个算例的设计变量、学科个数和耦合程度依次增加,但求解迭代次数没有明显增加,学科分析次数变化不大,说明随着设计变量及学科的增加、耦合的加强,本文所述方法均能具有良好的求解效率。
3)在方法的适应性方面,对于算例3中不同试验点和不同初值的情况,本文所述方法均能有效求解最小极限状态函数,证明该方法对试验点和初值点不敏感,具有良好的适应性。
4 结 论本文结合宽容分层序列法的思想,提出了随机与区间不确定性下的分层序列化MRA方法。将嵌套与序列化流程相结合,前期搜索采用概率可靠性分析嵌套区间机制分析的方式搜索初始区域,后期搜索采用序列化执行概率可靠性分析与区间机制分析的方式加快收敛过程。在区间模型可靠性分析中引入系统一致性约束,将MDA从概率多学科可靠性分析和区间多学科可奥性分析中剥离,并引入有效集拟牛顿法,在提高求解效率的同时确保了算法的适应性和全局收敛性能。通过算例验证了该方法求解混合不确定性下的多学科可靠性分析问题是可行且有效的,所提出的分层序列化MRA方法具有较好的计算效率、精度、收敛特性和适应性。该方法在前人的基础上进一步完善了随机与区间不确定性下的多学科可靠性分析方法。
| [1] | Agarwal H, Renaud J E, Lee J C, et al. A Unilevel Method for Reliability Based Design Optimization[C]//Proceedings of the 45th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, Reston, Va, 2004: 1-19 |
| [2] | 姜潮,郑静,韩旭,张庆飞. 一种考虑相关性的概率-区间混合不确定模型及结构可靠性分析[J]. 力学学报, 2014, 4(16): 591-600 Jiang Chao, Zheng Jing, Han Xu, Zhang Qingfei. A Probability and Interval Hybrid Structural Reliability Analysis Method Considering Parameters' Correlation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 4(46): 591-600 (in Chinses) |
| Cited By in Cnki (0) | |
| [3] | 吴钰龙,姜潮. 一种考虑模糊不确定性的概率-区间混合结构可靠性分析方法[J]. 机械强度, 2014, 4(16): 591-600 Wu Yulong, Jiang Chao. A Reliability Analysis Method for Structures with Hybrid Probability-Interval Considering Fuzzy Uncertainty[J]. Journal of Mechanical Strength, 2014, 36(3): 393-401 (in Chinese) |
| Cited By in Cnki (0) | |
| [4] | Guo Jia, Du Xiaoping. Reliability Analysis for Multidisciplinary Systems with Random and Interval Variables[J]. AIAA Journal, 2010, 48(1): 82-91 |
| Click to display the text | |
| [5] | 刘继红,安向男,敬石开. 随机与区间不确定性下的序列化多学科可靠性分析[J]. 计算机集成制造系统, 2013, 7(19): 1441-1446 Liu Jihong, An Xiangnan, Jing Shikai. Sequential Multidisciplinart Reliability Analysis with Random and Interval Uncertainty[J]. Computer Integrated Manufacturing Systems, 2013, 7(19): 1441-1446 (in Chinese) |
| Cited By in Cnki (3) | |
| [6] | Byeng D Youn, Kyung K. Choi, Young H. Park. Hybrid Analysis Method for Reliability-Based Design Optimization[J]. Journal of Mechanical Design, 2003, 6(125): 221-232 |
| [7] | Du Xiaoping. Efficient Methods for Engineering Design Under Uncertainty[D]. Chicago: University of Illinois, 2002 |
| [8] | Wong Elizabeth. Active-Set Methods for Quadratic Programming[D]. California: University of California, 2011 |
| [9] | Youn B D, Chol K K. Selecting Probabilistic Approaches for Reliability-Based Design Optimization[J]. AIAA Journal, 2004, 42(1): 124-131 |
| Click to display the text | |
| [10] | 易平. 概率结构优化设计的高效算法研究[D]. 大连:大连理工大学,2007 Yi Ping. Study on Efficient Algorithm of Probabilistic Structural Design Optimization[D]. Dalian: Dalian University of Technology, 2007 (in Chinese) |
| Cited By in Cnki (15) | |
| [11] | 张任远,黄俊. BLISS研究及其在飞机设计中的应用[J]. 飞机设计, 2007, 6(27): 1-6 Zhang Renyuan, Huang Jun. Research of BLISS and Its Application in Aircraft Design[J]. Aircraft Design, 2007, 6(27): 1-6 (in Chinese) |
| Cited By in Cnki (4) |


