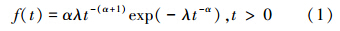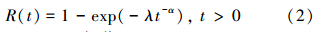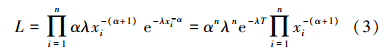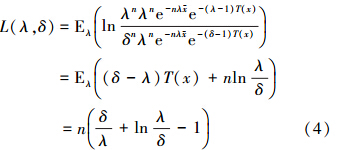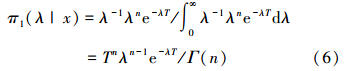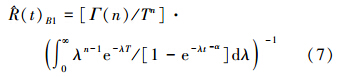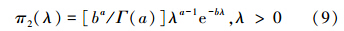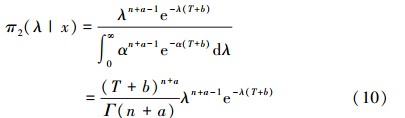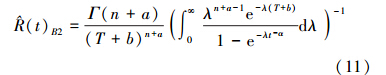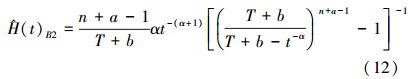2. 西安邮电大学 电子工程学院, 陕西 西安 710121
逆威布尔分布(记为IW(λ,α))是可靠性工程中一类重要且应用广泛的寿命分布[1]。该分布的密度函数、可靠度函数分别为
失效率H(t)=αλt-(α+1)exp(-λt-α)／[1-exp(-λt-α)],t>0,其中α>0为形状参数,λ为尺度参数。
近年来已有一些文献对逆威布尔分布进行了讨论,文献[2]基于平方损失函数,给出了逆威布尔分布的Bayes估计和预测。文献[3]基于屏蔽寿命数据,研究了逆威布尔型部件航空电源系统可靠性的估计问题,给出了逆威布尔型部件可靠性的Bayes估计和极大似然估计。文献[4]研究了逆威布尔分布次序统计量及其分布。在平方损失函数下,文献[5]给出了逆威布尔分布尺度参数的Bayes估计。平方损失函数是对称的,它给于高估和低估同等的重要性,然而这样的限制往往是不合实际的。例如,在估计产品的可靠性及失效率函数时,高估会比低估带来的后果更严重,在这种情况下使用对称损失函数是不合实际的。于是一些学者提出了非对称损失函数,例如Linex 损失函数及熵损失函数。
熵损失函数是Bayes分析中一种重要且使用较多的损失函数。但是,基于熵损失函数,对逆威布尔部件寿命参数、可靠性指标的Bayes估计及性质的研究尚未发现。本文在熵损失函数下讨论逆威布尔部件尺度参数、可靠度函数及失效率的Bayes估计及优良性质,并给出部件尺度参数的UMVUE。
1 一致最小方差无偏估计从一大批服从IW(λ,α)分布的部件中随机抽取n个,以X1,X2,…,Xn分别表示它们的寿命,则样本(X1,X2,…,Xn)的联合分布密度为
式中，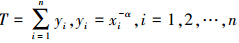
引理1 若T为参数λ的充分完备统计量,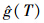
为g(λ)一个无偏估计,满足var(
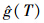) < ∞,对任意的λ∈Θ.则
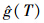是g(λ)的一致最小方差无偏估计,且在几乎处处意义下,该估计是唯一的[6]。
定理1 对IW(λ,α)分布,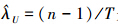
是λ的一致最小方差无偏估计,且在几乎处处意义下,该估计是唯一的。
证明 令Yi=Xi-α,则 P(Yi≤y)=P(Xi-α≤y)=P(Xi≥y-1／α)=1-e-λy,y>0即Yi服从指数分布exp(λ)。又由于Yi相互独立同分布,i=1,2,…,n,所以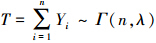 
。故 
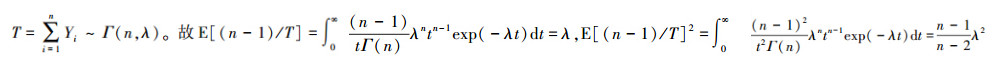。所以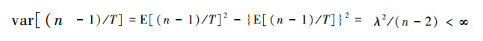 
。又由(3)式知T为λ的充分完备统计量。故由引理1知(n-1)/T为λ的一致最小方差无偏估计,且在几乎处处意义下是唯一的。证毕。
定义1 设随机变量X服从逆威布尔分布,其密度函数记为f(λ,x)。其中λ为参数,如果δ是λ的一个估计,则Iw(λ,α)分布的熵损失函数为
引理2 在损失函数(4)下,对于任意的先验分布π(λ),参数λ的Bayes估计为[6]
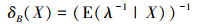
若Bayes风险R(δB(X) < +∞成立,则λ的Bayes估计还是唯一的.这里X=(X1,X2,…,Xn)。
2.1 无信息先验下的Bayes估计在参数估计中,当没有关于参数的任何其他历史信息时,可选用Jefferys无信息先验分布。由Jeffrey准则,先计算λ的Fisher信息量I(λ)。由(3)式知样本的对数似然函数为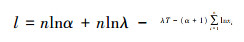 
,从而I(λ)=E(-∂2l／∂λ2)∝1/λ2,故选取λ的先验分布为
于是得λ的后验密度为
定理2 对IW(λ,α)分布,若取λ的先验分布为(5)式,则在损失函数(4)下,λ的唯一Bayes估计为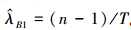
。
证明 由于E(λ-1|X)=∫0∞λ-1Tn[Γ(n)]-1
λn-1e-λTdλ=T／(n-1)。由引理2得λ的Bayes估计为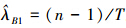 
。 
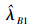的唯一性证明可参考下文中的定理4,这里略去。
定理3 对IW(λ,α)分布,若取λ的先验分布为(5)式,则在损失函数(4)下,可靠度R(t)与失效率H(t)的Bayes估计分别为
证明 这里只证明(8)式,(7)式可类似证明。因为
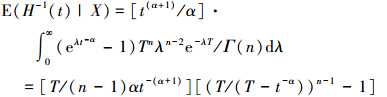
再由引理2得H(t)的Bayes估计为
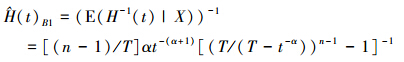
若参数λ的先验分布选取为共轭先验分布Γ(a,b),其分布密度为
式中，a,b>0。则可计算得λ的后验分布密度为
定理4 对IW(λ,α)分布,若λ的先验分布选为(9),则在熵损失函数下,λ的唯一Bayes估计为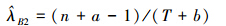 
证明因为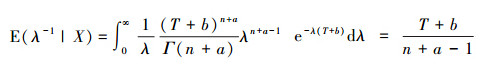 
,再由引理2得 
。
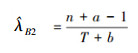下面证明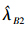 
的Bayes风险是有限的。
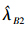的风险为
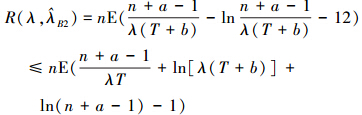
易知熵损失函数为凸函数,故根据Jensen不等式
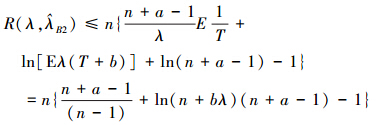
所以 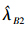的Bayes风险为
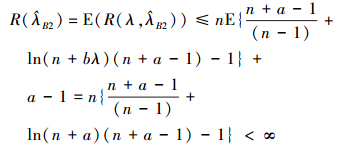
故在凸损失函数(4)下, 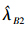是唯一的。证毕。
定理5 对IW(λ,α)分布,若取λ的先验分布为(9)式,则在损失函数(4)下,可靠度R(t)、失效率H(t)的Bayes估计分别为
证明 这里只证明(12)式,(11)式可类推。
因为
再由引理2得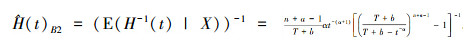 
。
引理3 在给定的Bayes决策问题中,若对给定的先验分布π(λ),λ的Bayes估计是唯一的,则它是容许的[6]。
定理6 对IW(λ,α)分布,若分别取(5)式、(9)式为λ的先验分布,则在熵损失损失函数下,λ的Bayes估计都是容许的。
证明 事实上,由定理2、定理4可知在熵损失损失函数下,其Bayes估计都是唯一的。再由引理3得其Bayes估计是容许的。证毕。
下面考虑λ的形如[cT+d]-1的估计类的可容许性。
从上面的讨论我们注意到,在适当的Γ-先验分布下,形如[cT+d]-1的估计都是λ的Bayes估计,下面对c和d的不同取值情况分别进行讨论。以下令c*=1／(n-1)。
定理7 当0≤c < c*,d>0,n>1时,估计[cT+d]-1是可容许的.
证明由定理3知,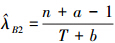 
是容许的。当a>0,b>0,n>1时,有0 < (n+a-1)-1 < (n-1)-1,只需取a=1/c+1-n,b=d/c,便得到估计[cT+d]-1,从而证明了[cT+d]-1是容许的。
当c=0,d>0时,由于它是取常值估计,故[cT+d]-1是可容许的。
定理8 当c=c*,d≥0,且λ的Bayes估计量的风险函数关于λ是连续时,则估计量[cT+d]-1是可容许的。
证明 当d=0时,[cT+d]-1=(n-1)/T=
,由定理6知[cT+d]-1是可容许的。下证d>0情况。取λ的先验分布为,则在熵损失函数下,λ的2个Bayes估计为δk(T)与δ(T)的Bayes风险函数之差为
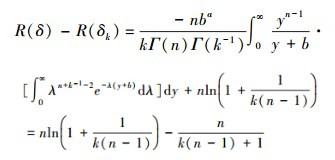
当k→∞时,R(δ)-R(δk)→0,再由文献[7]及已知条件知[cT+d]-1是可容许的,证毕。
3 数值模拟给定α,λ真值,运用Monte-Carlo方法产生容量为n且服从逆威布尔分布的样本。利用该组数据给出参数λ的一致最小方差无偏估计,λ及可靠度R(t)、失效率H(t)的贝叶斯估计。重复上述模拟1 000次,分别计算各种估计的均方误差。模拟结果列于表 1。
| n |
|
|
|
|
|
|
|
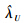
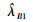
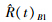
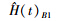
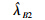
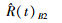
| 10 | 0.194 7 | 0.194 7 | 0.030 5 | 0.036 5 | 0.095 7 | 0.008 8 | 0.035 8 |
| 20 | 0.172 7 | 0.172 7 | 0.025 9 | 0.033 2 | 0.059 1 | 0.007 9 | 0.029 5 |
| 30 | 0.165 0 | 0.165 0 | 0.023 2 | 0.029 3 | 0.056 7 | 0.006 1 | 0.026 8 |
| 40 | 0.152 6 | 0.152 6 | 0.021 3 | 0.019 7 | 0.048 7 | 0.005 8 | 0.023 5 |
| 50 | 0.152 5 | 0.152 5 | 0.020 2 | 0.017 9 | 0.045 2 | 0.004 9 | 0.017 7 |
| 100 | 0.145 9 | 0.145 9 | 0.019 6 | 0.016 8 | 0.042 6 | 0.004 0 | 0.009 9 |
由表 1中数据可以看出:(1)当样本量相同时,共轭先验下贝叶斯估计均方误差最小,精度最高,其次是无信息先验下贝叶斯估计,这与我们的理论推导是吻合的。因为Bayes估计不仅使用了样本信息,也运用了先验信息,所以Bayes估计精度应该比UMVUE高。(2)当样本量比较小时,Bayes估计的均方误差小于UMVUE的均方误差.随着样本量的增加,各个估计均方误差都减小。但在共轭先验下的Bayes估计均方误差最小,故在工程实际中应在共轭先验下,使用Bayes方法进行可靠性分析。
4 结 论本文给出了逆威布尔部件寿命参数的一致最小方差无偏估计,参数及可靠性指标的Bayes估计,并证明了形如[cT+d]-1的一类估计的容许性。文中还利用随机模拟方法给出数值例子,结果表明在共轭先验分布下,贝叶斯估计均方误差最小,估计效果最好,在小样本下效果尤其明显。
| [1] | Khan M S, Pasha G R, Pasha A H. Theoretical Analysis of Inverse Weibull Distribution[J]. Wseas Trans on Mathematics, 2008, 7(2): 30-38 |
| [2] | Kundua D, Howlader H. Bayesian Inference and Prediction of the Inverse Weibull Distribution for Type-II Censored Data [J]. Computational Statistics and Data Analysis, 2010, 54(6):1547-1558 |
| Click to display the text | |
| [3] | 张帆, 师义民. 基于屏蔽数据的航空电源系统可靠性分析[J]. 航天控制, 2009, 27(4):96-100 Zhang Fan, Shi Yimin. Parameter Estimation of the Aerospace Power Supply System Using Masked Lifetime Data[J]. Aerospace Control, 2009, 27(4): 96-100 (in Chinese) |
| Cited By in Cnki (8) | Click to display the text | |
| [4] | Mahmouda M A W, Sultana K S, Amerb S M. Order Statistics From Inverse Weibull Distribution and Associated Inference[J]. Computational Statistics & Data Analysis, 2003, 42: 149-163 |
| Click to display the text | |
| [5] | 苏韩,韦程东,韦师,邓立凤. 平方损失下逆威布尔分布参数的Bayes估计[J]. 广西师范学院学报: 自然科学版, 2009, 26(4): 32-35 Su Han, Wei Chengdong, Wei Shi, Deng Lifeng. The Bayes Estimation of Inverse Weibull Distribution Parameter under Square Loss Function[J]. Journal of Guangxi Teachers Education University: Natural Science Edition, 2009, 26(4): 32-35 (in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [6] | Berger J O. Statistical Decision Theory and Bayesian Analysis[M]. New York, Springer-Verlg, 1985 |
| [7] | 茆诗松. 贝叶斯统计[M]. 北京:中国统计出版社, 1999 Mao Shisong. Bayesian Statistics [M]. Beijing: China Statistics Press, 1999 (in Chinese) |
2. School of Electronic Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710121, China