2. 西安财经学院统计学院, 陕西西安 710100
对称是一种自然美,工程与自然界到处可见对称图形,难怪典型非线性动力学模型,例如Duffing振子、Van der Pol振子与Mathieu振子都具有一定对称性。本文先以简谐外激Duffing系统为例、详细推介周期对称破裂分岔的发生机理。然后再以简谐参激双势阱Duffing系统为例,进一步阐明混沌对称破裂激变的发生机理与特色。分岔与激变是非线性动力学系统特有的行为现象。分岔通常指系统的规则运动随系统关键参数微变而发生的突变;激变(crisis)则约定为系统的混沌运动随着系统关键参数的微变而发生的突变。可以毫不夸张地说:对称破裂分岔是对称系统走上通向混沌道路的第一步。其后,随分岔参数的逐步变化,系统再借倍周期分岔序列串才跨入混沌大门,开始了混沌那种不断再现、既无限自相似、又永不重复、且持有正的最大Lyapunov指数(TLE)特征的漫长征程[1, 2]。
1 对称破裂分岔简谐外激下的经典Duffing系统的运动微分方程可表示为[3]
式中:a,c为正常数,力幅F或频率ω可作为分岔参数来考察系统响应的变化。图1给出:当ω= 0.935时系统(1)有一个原点自对称周期轨; 当ω= 0.945时有一对原点互对称周期轨,其中y≡ 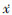 ,全文同。所以,在此分岔参数变化区间内,系统一定发生过一次对称破裂分岔。文献[3]指出:对称破裂分岔应发生在系统的TLE取零极大值处。
,全文同。所以,在此分岔参数变化区间内,系统一定发生过一次对称破裂分岔。文献[3]指出:对称破裂分岔应发生在系统的TLE取零极大值处。
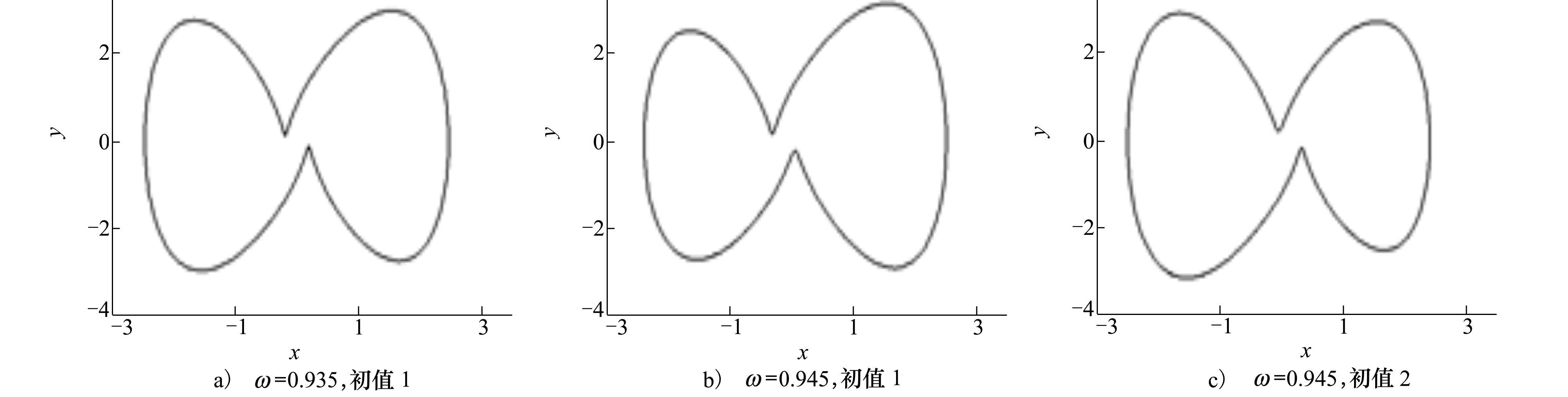 |
| 图 1 系统(1)取不同初值所对应的对称周期轨道 |
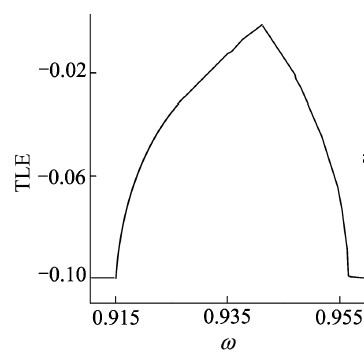 |
| 图 2 TLE于ω=0.941 |
 |
| 图 3 周期鞍S及其稳出现零极大值定与不稳定流形 |
仿真研究显示:非线性动力学系统一旦闯入混沌世界,随后发生的一切变化都会打上混沌的烙印,即使瞬态混沌的周期终态也往往徒具规则的形式,连对应的吸引域也都是分形的。鉴于参激情形的动力学行为一般比外激情形的更为丰富,下面讨论对称破裂激变(简称SB激变)时改用参激双势阱Duffing系统,其无量刚常微分方程可表示为
式中:x表示所考察的物理量,t表示时间,ω表示参激频率,μ为参激强度兼分岔参数,a,b,c都是正的常参数;再设这些参数的选取保证了系统解存在唯一性和遍历性,且c>0保证了系统的耗散性。从方程(2)可见:①原点不仅是鞍奇点,也是对称中心;②假设x(t)是系统的解,不论周期的或混沌的,那么-x(t)必定也是系统的解;而且二者在(x,y)相平面上的2条相轨是关于原点互对称的。当x(t)的相轨本身就是原点对称时,二者合而为一。这就是Duffing系统本身的对称性,它不依赖于激励的形式。而系统周期相轨的“分”与“合”只是反映其“自”原点对称与“互”原点对称形式之间的切换而已。对于周期相轨来说,这是显而易见的。但对于混沌Poincaré图来说,就不那么一目了然;何况混沌Poincaré图本身都是分形的。再说混沌激变本身有其特殊性:一般说来,混沌激变多半发生于持久混沌与瞬态混沌之间的交替切换。所谓瞬态混沌是指在远短于其生命历程的时段内呈现类似混沌的行为,但最终又不得不回归到规则运动。所以,在分岔图中出现的“周期窗口”往往就是瞬态混沌与持久混沌相互转化的天下。它正好有助于实现混沌激变的“自”、“互”原点对称切换。还值得一提的是和瞬态混沌相伴随的混沌鞍,它是一般初学者不熟悉的。如果说周期鞍是周期吸引子丧失了吸引性后在Poncaré平面上留下的烙印,那么,混沌鞍就是原混沌吸引子丧失了吸引性后在Poncaré平面上留下的烙印。但人们不应小觑它在混沌动力学分析中的作用[4],其实,烙印只是它的一面,它的另一面后文再说。众所周知,混沌吸引子对应于动力系统的不动点闭集;而混沌鞍则对应于不动点开集。前者具有吸引性,因而计算比较简单,广泛用于系统定态分析;后者则必须仰仗图-胞映射等专业工具[5]。非线性动力学系统的特点之一是:一个系统可能同时共存多个具有不同形态和特色的解。系统(2)就存在2类独立的共存解,所以,采用多重分岔图与多重TLE图来进行定态运动分析研究[6]。图4与图5分别给出了μ=4.9~7.2时,系统(2)的多重分岔图与多重TLE图。需要补充说明的是:本系统首次进入混沌早发生于μ=0.3附近,远离本文考察范围。所以,本节所示周期解都指瞬态混沌的“终态”。图4与图5中对应于TLE大于零的是2大混沌区,其余都是瞬态混沌的活跃区,包括混沌区中出现的“周期窗口”,它们通常是酝酿和发生分岔与激变的重要场所。下面粗略分7步来介绍考察范围内一些重要分岔与激变的演化。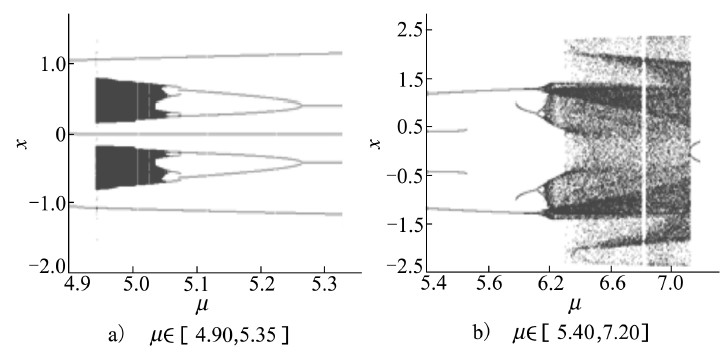 |
| 图 4 μ=4.9~7.2范围内,系统(2)的多重分岔图 |
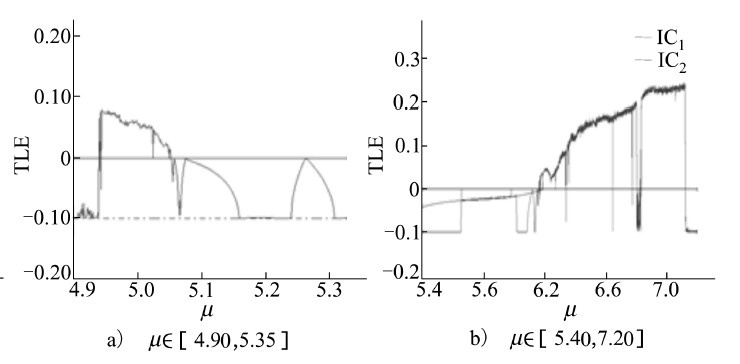 |
| 图 5 μ∈[4.90,5.35]范围内,系统(2)的多重TLE图 |
第1步 图4左侧的过渡区本来就遗留有一个定态周期吸引子和一个相伴的大混沌鞍,当时,从该大混沌鞍分裂出一部分,首先通过边界激变原地转化为一双互原点对称的持久混沌吸引子,而原共存的终态周期吸引子仍保持不变;
第2步 新生混沌吸引子通过内部激变适度收缩,但仍保持其正的TLE,直到μ=5.05;
第3步 当μ=5.05,系统TLE由正到负横穿零值,发生边界激变,混沌吸引子转化为新的定态mT多周期吸引子;随后发生半周期分岔序列串;当变成1T周期吸引子时,暂停后又重启倍周期分岔序列串;它们都属于广义对称破裂分岔;
第4步 直到当μ=6.20,系统TLE由下向上横穿零值时,再次发生边界激变,生成一对新生的互为原点对称的混沌吸引子;与之一起,原共存的一对1T周期吸引子也通过边界激变生成另一对新生的互为原点对称混沌吸引子;
第5步 这2对新生混沌吸引子又借吸引子融合激变在μ=6.291 4处合成唯一与原点自对称的大混沌吸引子;实现了一次 Poincaré 图形结构的SB破裂激变;
第6步 之后混沌吸引子继续发展壮大,系统TLE继续稳步上扬,并通过一个稍大一点的周期窗口,TLE急剧上升到一个新的更高的台阶;其间发生了这是一次边界激变吸引子融合激变兼内部激变;
第7步 一直到μ=7.121处,系统TLE再次急转直下,该自对称的大混沌吸引子又整体SB激变为一原点自对称2T周期吸引子与相应的混沌鞍。
关于这μ=6.802 6~6.831 8的周期窗口,文献[7]已有详情介绍,此处不再赘述。值得一提的是在这个窗口里,几乎复现了μ=4.90~7.20范围内发生过的典型分岔与激变。为更好地研究图5左侧有关“窗口”内混沌的演化,先细化对应于μ=5.00~5.07的TLE图。
从图6可见,在μ=5.025与在μ=5.050处分别出现2个V形混沌缺口,不妨取前一个缺口试考察。图7是与之对应的混沌演化图,这里又分层为几个细部,基本上都属于类似的演化模式。图8是图7中μ=5.025附近的某个细部的放大图。从图8可见,细部内混沌吸引子应该处于收缩态势。图9与图10分别是μ=5.024 8与μ=5.025 0处的系统Poincaré图,对比看来其混沌吸引子的规模与分布确有明显改观,它证实了在此μ值区间内系统发生过内部激变。尽管Poincaré图形有所突变,但系统运动的原点对称性保持不变。
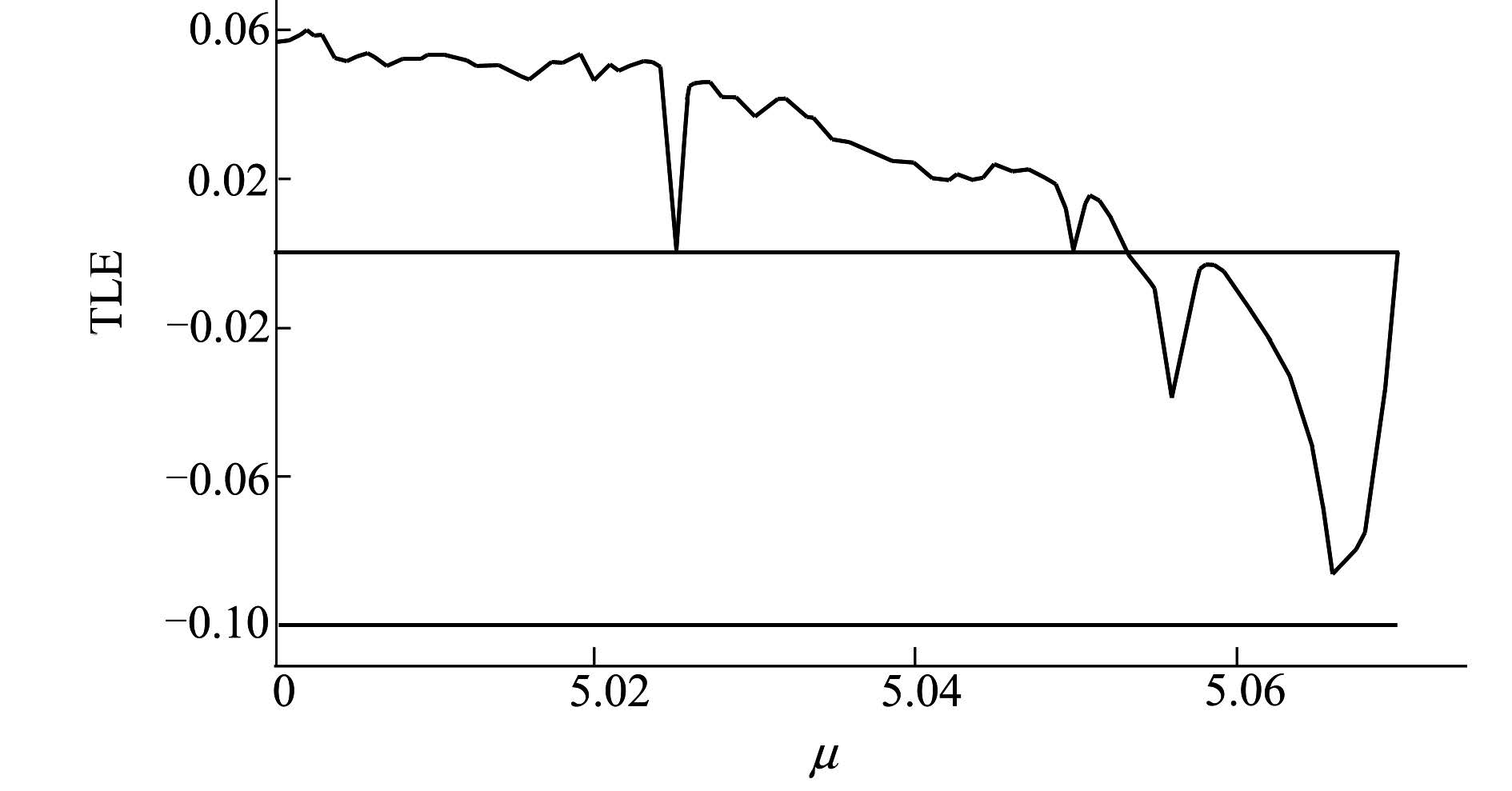 |
| 图 6 μ=5.00~5.07时,系统(2)的多重TLE图 |
 |
| 图 7 μ=5.025附近的混沌演化图 |
 |
| 图 8 对应于图7某个细部的放大图 |
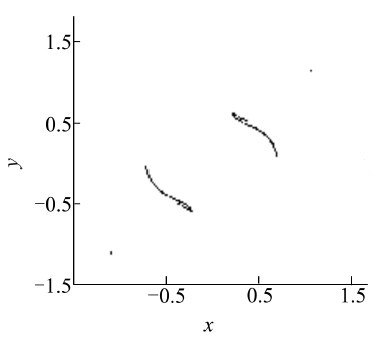 |
| 图 9 μ=5.024 8处系统Poincaré图 |
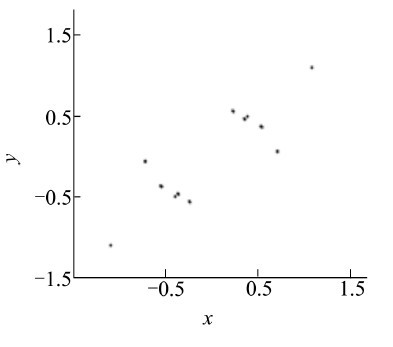 |
| 图 10 μ=5.025 0处系统Poincaré图 |
其实研究系统SB激变最直接的方法还是全面充分考察各个关键映射截面处的Poincaré图或相空间格局图。例如,图11a)所示为μ=4.94时的相空间格局图,标有一对互原点对称的终态周期吸引子A(1)与A(2),其余为互原点对称的一对混沌鞍。图11b)为μ=4.95时的相空间格局[7],保留了A(1)与A(2),新增了互原点对称的一对混沌吸引子A(3)与A(4),并在原地消去了原相应那部分混沌鞍。这清楚说明了这次边界激变所发生的一切。再如,图12a)除给出μ=6.291 3时已成熟的一对互原点对称持久混沌吸引子A(1)与A(2)外,还有对应于“正孕育混沌发展”的混沌鞍。而图12b)所示只剩下了μ=6.291 5时,由周围邻域中初始条件一致确定的唯一自原点对称混沌吸引子。可见,在这期间系统发生过吸引子融合激变是铁定的[7]。图12c)与图12d)分别给出μ=6.30与μ=6.40时的混沌吸引子,对照图12d)与图12a),不难联想到混沌鞍还有的另一面:它往往也是持久混沌的一个“预兆”。
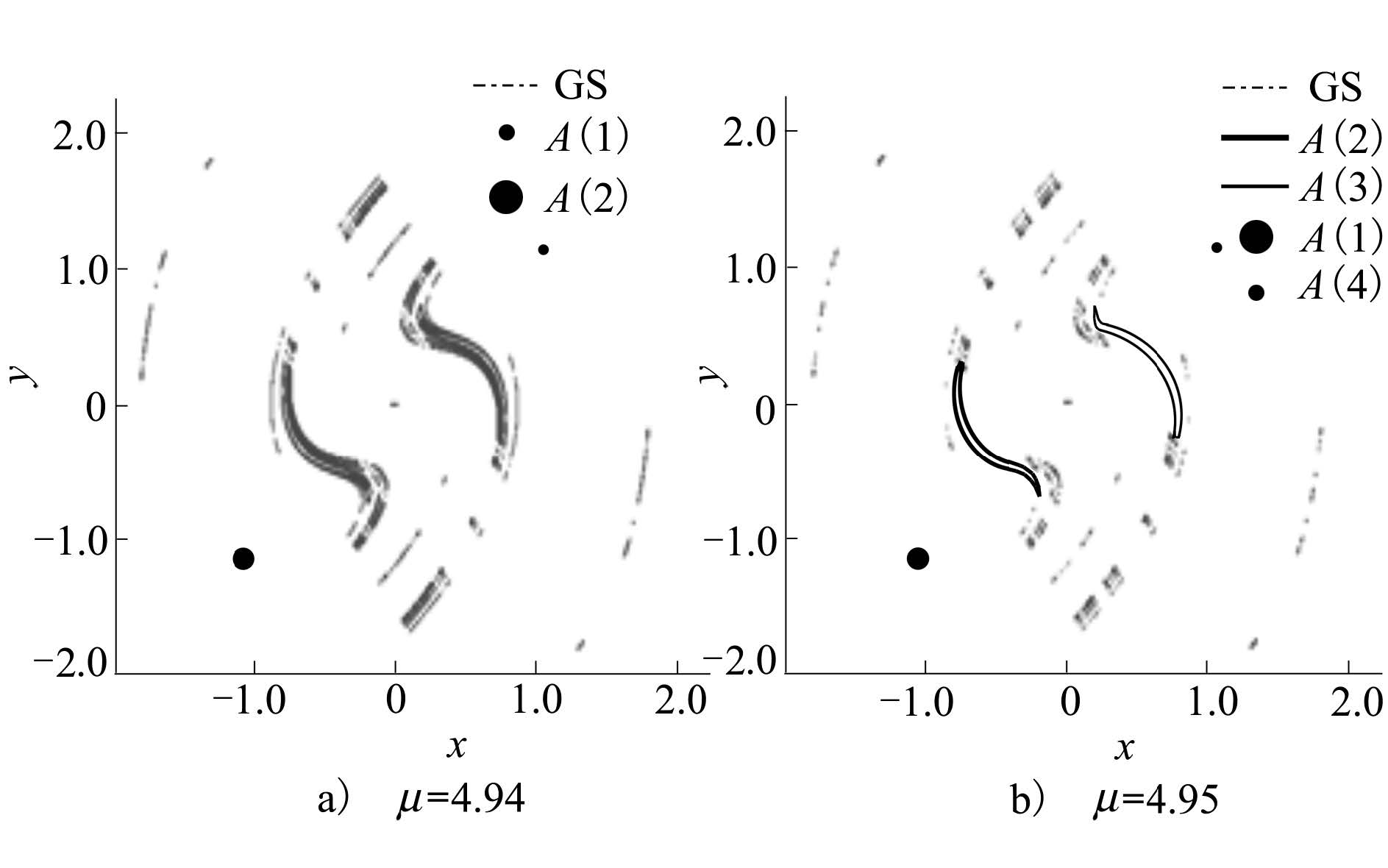 |
| 图 11 μ取不同值时系统(2)的吸引子及混沌鞍 |
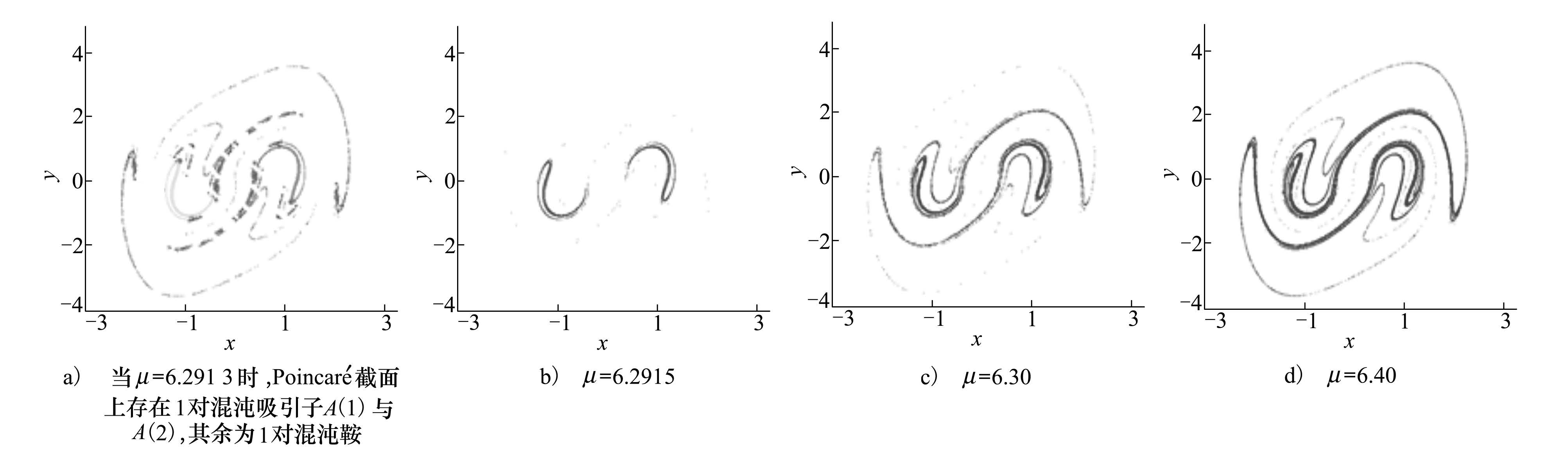 |
| 图 12 μ取不同值时系统(2)的Poincaré |
通过全面重温Duffing系统中的SB分岔与激变,重新认识非线性动力系统中的SB周期分岔与SB混沌激变的一般规律,达到了“温故而知新”的实际效果。我们补充说明了系统TLE图上V形混沌缺口内发生的内部激变;特别是对混沌鞍在混沌世界内的客观存在和它在孕育混沌发展过程中的潜在作用,有了更深入的认识。希望本文有关混沌发展与激变深入浅出的阐述能有助于更多读者进入通向混沌动力学的大门。
| [1] | Fang T, Dowell E H. Numerical Simulations of Periodic and Chaotic Responses in a Stable Duffing System[J]. International Journal of Nonlinear Mechanics, 1987, 22(5): 401-425 |
| Click to display the text | |
| [2] | 方同. 有关混沌及其控制与同步的一些理解[J]. 振动工程学报, 2007, 20(5): 447-452 Fang T. Understanding of Chaos Together with Its Control and Synchronization[J]. Journal of Vibration Engineering, 2007, 20(5): 447-452 (in Chinese) |
| Cited By in Cnki (9) | |
| [3] | Fang T, Zhang Y. Insight into Phenomena of Symmetry Breaking Bifurcation[J]. Chinese Physics Letters, 2008, 25(8): 2809-2811 |
| Click to display the text | |
| [4] | Tyrkiel E. On the Role of CS in Generating Chaotic Dynamics in Nonlinear Driven Oscillators[J]. International Journal of Bifurcation and Chaos, 2005, 15(4): 1215-1238 |
| Click to display the text | |
| [5] | Yue X L, Xu W, Zhang Y. Global Bifurcation Analysis Rayleigh-Duffing Oscillator through the Composite Cell Coordinate System Method[J]. Nonlinear Dynamics, 2012, 69: 437-457 |
| Click to display the text | |
| [6] | Zhang Y, Lei Y M, Fang T. Symmetry Breaking Crisis of Chaotic Attractors[J]. Acta Physica Sinica, 2009, 58(6): 3799-3805 |
| Click to display the text | |
| [7] | Zhang Y, Rossetto B, Xu W, Yue XL, Fang T. Roles of Chaotic Saddle and Basin of Attraction in Bifurcation and Crisis Analysis[J]. International Journal of Bifurcation and Chaos, 2011, 21(3): 903-915 |
| Click to display the text |
2. School of Statistics, Xi'an University of Finance & Economics, Xi'an 710100, China