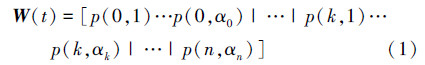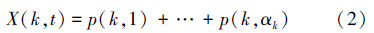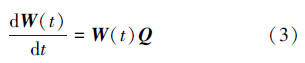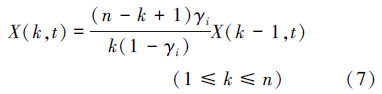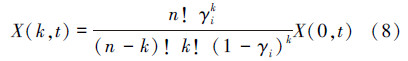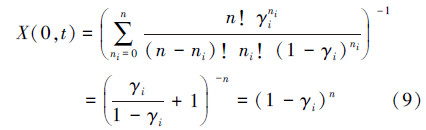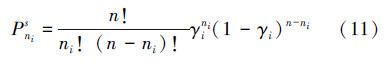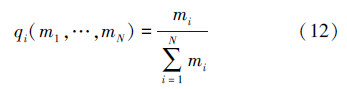群集机器人系统强调控制与协调大规模的简单机器人完成指定任务。就任务分配这个机器人协作领域的重要问题而言，除了涌现式分配，原先应用于多机器人系统的集中式和基于协商的分配方法在群集系统中已不再适用。涌现式分配使用简单的局部规则完成全局行为。如Correll等[1]提出一种模拟节肢动物局部交互的方法，将群集机器人分配到不同规模的聚集。Kernbach等[2]设计了一种受启发于蜜蜂热聚合行为的方法，不使用任何通信就可根据区域光源的强度和面积分配属于该区域机器人的数量。
随着群集机器人工程复杂化，设计局部规则得到期望的全局输出变得越来越困难。因此，建立模型预测全局行为是否与预期一致近年来受到学术界的普遍重视。Hamann等[3]提出使用统计物理中的Fokker-Planck方程描述群集机器人的动力学行为。但是为了简化模型中的多维方程，采取令某些变量取常数的做法只能得到特殊情况下的预测。文献[4]提出一个基于过程代数的Bio-PEPA框架。虽然可以同时建立研究机器人之间交互的微观模型和研究群集整体性质的宏观模型，但是它仅通过实验结果说明了对群集进行微观与宏观分析结论的一致性，该方法并没有提供发现群集机器人系统新规律和改善系统性能的手段。文献[5]提出了一种用于任务分配的宏观模型，但其只考虑了2种任务类型的分配问题，当任务类型多于2种时该模型便不适用，因此不具备灵活性和可扩展性。
针对以上问题，我们需要寻求一种不通过降维就可得到描述群集任务分配方程的解，可以发现机器人群集行为新统计规律，且不受群集规模和任务类型限制的新模型。本文使用二维马尔可夫动态系统中的拟生灭过程建立宏观任务分配模型，任务类型是参数N，求得了模型在稳态的闭式解，发现了群集系统任务分配结果服从二项分布这个规律，定性的证明了系统性能和群集规模的2种新关系。
1 系统宏观模型的建立与分析 1.1 任务分配问题描述假设在工作场地中总共有N种类型的任务，表示为集合I=｛i|1,2,…,N｝,相应的每个机器人都有N种任务状态,简称“状态”。在一个时间段内机器人只能属于其中一种状态。通过在场地中随机游走和局部观察,机器人逐步学习各种不同任务在环境中所占的比例。一个长度为h的滚动历史窗口负责以先进先出的方式存储观察结果。机器人对状态的更新由局部规则决定,称之为转移函数,求其值需要访问历史窗口。任务分配对个体机器人来说是要求其满足一种与环境保持一致的行为结构,以保证群集执行任意一种任务的比例等于该任务在环境中的原始比例。
在作者先前的工作[6]中,分别通过基于随机过程的证明和真实场景的机器人实验(如图1所示)预测并验证了机器人系统执行任务r和任务g数量的比例等于各任务在环境中的原始比例。为了解决任务类型参数化问题,作者在文献[7]中建立了任务类型为N的个体机器人任务分配模型。本文继续先前的研究,提出的新宏观模型不但保持了任务类型为N的优点,还发现了群集分配效果的期望和方差与群集规模的关系。
 |
| 图 1 机器人系统任务分配行为的视频截图 |
群集中有n个成员,每个机器人都要执行N种类型的任务。个体状态转移函数值qi应反映各类型任务在全体任务中的比例信息,即对于∀i∈I,有qi∝Mi/M0=μi,其中M0为所有类型任务数量之和,μi为第i类任务在全体任务中的比例。但由于传感器限制,机器人没有关于任务的全局信息,它们通过对局部观察信息反复的带有冗余的叠加来估计全局。即用局部估计Kloc=｛m1,…,mi,…,mN｝代替全局知识Kglob=｛M1,…,Mi,…,MN｝。
定理1 假设机器人处于任务状态i的概率演化规律由马尔可夫过程“增益-损失”主方程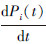 
描述。则表示机器人任务分配结果的状态概率向量P(t)的解析表达式为
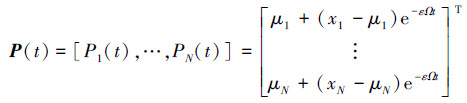
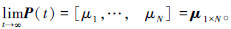
推论1 设n代表群集中机器人的数量,则处于状态空间I中各种状态的机器人数量占总数比例的平均值为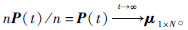 
这说明群集机器人任务分配的平均长期行为趋近于环境中各种任务占总任务量的原始比例。
在N维笛卡尔坐标系中,定义向量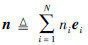 
=(n1,n2,…,nN)表示群集机器人系统的状态,其中 
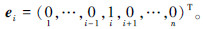随机整数变量ni表示执行第i种任务的机器人数量,取值范围为0≤ni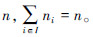 
令X(n,t)表示群集机器人系统在时间t处于状态n的概率,其边缘概率密度函数X(ni,t)表示群集机器人系统在时间t有ni个机器人执行第i种任务的概率。
由于在群集机器人系统中,不论是在个体数量n,还是在任务类型的种类N比较大的情况下,列举所有系统状态(n1,n2,…,nN)都是不可能的。使用以下2个应对策略分析:
策略1 使用N维概率密度函数X(n,t)的边缘概率密度函数X(ni,t)描述系统动态特性。
矩阵分析法是分析和建立随机过程模型的有用工具,它的主要思想是将马尔可夫过程转移速率矩阵中具有相同规律的元素分块,而不是单独处理每个元素。
策略2 首次将矩阵分析法[8]引入群集机器人系统的研究中。
对于N种任务类型中的任意一种,即∀i∈I,按照以下步骤建立群集机器人的系统状态模型。
步骤1 分组:将群集机器人系统的所有系统状态,按照随机变量ni的值从小到大的顺序,划分到n+1个组中,其中每组的系统状态都具有相同的ni值。
步骤2 构造L-P坐标系:首先创建横坐标轴并命名为“水平”(level),记作L-axis;再创建纵坐标轴并命名为“阶段”(phase),记作P-axis。在L-P二维坐标系中用属于某水平的阶段来表示群集机器人系统的系统状态,水平由沿着P轴的列表示,与每个水平对应的ni的值是沿着L轴增加的,阶段对应于每个水平中的行。
步骤3 建立二维马尔可夫模型:在构造的L-P坐标系中,用二维马尔可夫过程｛ψ(t),E(t),t≥0｝表示群集机器人系统在时刻t所处的状态。
经分析可得二维马尔可夫过程｛ψ(t),E(t),t≥0｝的性质可以归纳为:
性质1 属于每个水平的所有阶段都具有相同的ni的值。
性质2 第k个水平共有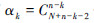 
个阶段,其中k=0,1,…,n。
性质3 状态空间是二维的,记作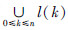 
,其中l(k)=｛(k,1),(k,2),…,(k,αk)｝,且αk表示第k个水平中阶段的最大序号。
假设在时间Δt内超过一个机器人进行状态转移的概率为ο(Δt),所以ni值的变化幅度为ni±1。因此二维马尔可夫过程｛ψ(t),E(t),t≥0｝成为一个“拟生灭过程”(quasi-birth-and-death process,QBD)[9]。阶段可以用二维标识符来索引,也可以用一维标识符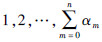 
索引。
拟生灭过程｛ψ(t),E(t),t≥0｝的转移速率矩阵Q是一个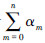 
阶方阵,如图2所示,其中记号al,…,hl标示子矩阵的起始点。矩阵外层记号代表水平,内层记号代表阶段。当n很大时,确定每两个阶段之间的转移速率是不可能的,因此确定Q中的每个矩阵元素也是不可能的。这里借用矩阵分析法的主要思想将转移速率矩阵中具有相同规律的元素分块,将一个子块的元素看做一个整体处理。因此考虑将矩阵Q的元素按照其所属的水平分块。首先将Q按照行的方向以间隔α0,…,αk,…,αn划分。如性质2所述,αk是拟生灭过程｛ψ(t),E(t),t≥0｝属于第k个水平的总阶段数;然后将Q按照列的方向以间隔α0,…,αk,…,αn划分,这样以来Q就被划分成了(n+1)2个块。被划分后的Q是一个拟块三对角矩阵(quasi-block tridiagonal matrix),即在主对角线上有子矩阵S0…Sn,在对角线下方有子矩阵M1…Mn,在对角线上方有子矩阵N0…Nn-1,其它的分块子矩阵都是零矩阵。
 |
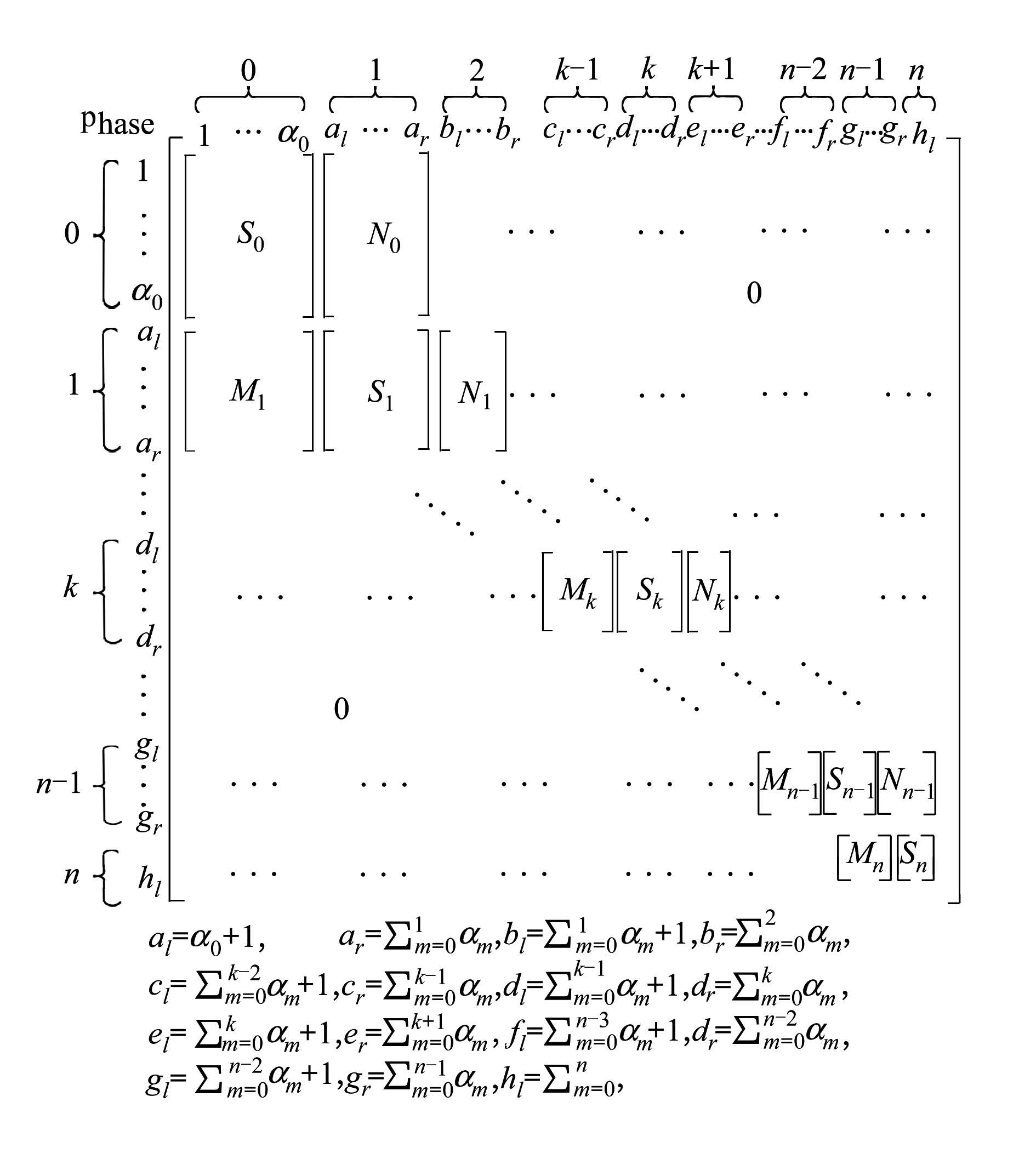| 图 2 转移速率矩阵Q |
对于∀i∈I,γi表示群集机器人系统中个体机器人处于状态i的概率。对于k=0,…,n和j=1,…,αk,令Mk[j·],Nk[j·],Sk[j·]分别表示矩阵Mk,Nk,Sk中第j行元素。bk,ak,sk分别是Mk[j·],Nk[j·],Sk[j·]的元素和。
命题1 当1≤k≤n-1时,有如下结论:1)矩阵Mk是一个αk×αk-1阶的子矩阵,Mk[j·]对应着从系统状态(k,j)到水平k-1的所有阶段l(k-1)的转移速率,矩阵Mk任意一行的和等于bk=k(1-γi);2)矩阵Nk是一个αk×αk+1阶子矩阵,Nk[j·]对应着从状态(k,j)到水平l(k+1)的转移速率,矩阵Nk任意一行的和等于ak=(n-k)γi;3)矩阵Sk是一个αk阶方阵,Sk[j·]对应着从状态(k,j)到水平l(k)的转移速率,根据转移速率矩阵的特性,矩阵Q的任意一行所有元素的和都等于零,所以矩阵Sk任意一行的和等于sk=-(ak+bk)。
同理,当k=0时,矩阵N0任意一行的和等于a0=nγi,S0任意一行的和等于s0=-a0。当k=n时,矩阵Mn任意一行的和等于bn=n(1-γi),Sn任意一行的和等于sn=-bn。
1.5 宏观模型推导与求解 定理2 已知γi(i∈I)为个体机器人处于状态i的概率,当拟生灭过程｛ψ(t),E(t),t≥0｝处于稳态时,在群集机器人系统中有ni个机器人处于状态i的概率为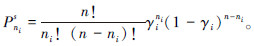
证明 考虑拟生灭过程｛ψ(t),E(t),t≥0｝,定义概率向量W(t)表示群集机器人系统在时刻t处于该过程所有阶段的概率。为了使公式推导更直观,我们使用竖线将所有阶段按水平分隔开,设k表示水平的序号,αk表示第k个水平中阶段的最大序号,则分割后的向量W(t)为:
定义群集处于每个水平的概率X(k,t):
对于矩阵Q的所有子矩阵,定义矩阵变换f把每个子矩阵的所有列都加到它的第一列。f(Q)使得Q的零子矩阵变成了零向量,非零子矩阵Mk,Sk,Nk变为向量Mk*,Sk*,Nk*:
1) 当1≤k≤n-1时,
2) 当k=0时,
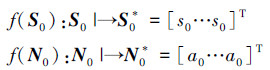
3) 当k=n时,
。
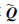拟生灭过程｛ψ(t),E(t),t≥0｝的主方程的矩阵形式是:
在｛ψ(t),E(t),t≥0｝处于稳恒态时,有稳恒态方程:
因此从公式(4)很容易推出:
由公式(5)确定的关于阶段的方程组中含有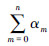 
个方程。已知αk是属于第k个水平的最大阶段数,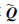的每个非零子矩阵都是元素相同的一个αk行向量,因此在与向量W(t)做矩阵乘法时可以提取相同项为公因式,代入公式(1)、(2)后,关于阶段的方程组被合并成了关于水平的方程组,含有n+1个方程,如(6)式所示:
由公式(6)可以得到递推公式(7)
并且最终可得:
群集机器人系统处于所有水平的概率和为1,所以有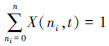 
,称之为归一化公式,代入公式(8)到归一化公式,可得:
将公式(9)代入(8),可得在｛ψ(t),E(t),t≥0｝处于稳恒态时群集机器人系统
处于每个水平的概率X(t)为:
综合公式(9)和(10)可得以下公式推导结果:在系统处于稳态时,对于∀i∈I,在群集机器人系统中有ni个机器人处于状态i的概率为:
2 群体规模与任务分配结果的关系
推论2 群体规模与任务分配结果期望值的关系:已知在拟生灭过程｛ψ(t),E(t),t≥0｝处于稳恒态时,随机变量ni表示处于群集机器人系统的状态空间中任意一个状态i的机器人数量,ni服从一个二项分布,即ni～B(n,γi),其中γi表示个体处于状态i的概率,有γi=Pi(t)其中Pi(t)是由定理1给出的P(t)=P1(t),…,Pi(t),…,PN(t)的第i个分量。那么E(ni)=nγi,因此处于状态i的机器人在群集中所占平均比例为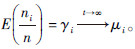 
由此我们可以推出理论上,群集任务分配结果的数学期望与系统中机器人的数量n无关。此外这个期望值与推论1一致。
推论3 群体规模与任务分配结果方差的关系:由ni～B(n,γi)可知处于状态i的机器人数量在群集中所占比例的方差为 
μi))。可以推出对于相同的环境条件μi,群集任务分配结果的方差与系统中个体机器人的数量n呈反比例的关系,即n越大,方差越小,任务分配的结果越集中在数学期望附近;反之n越小,方差越大,任务分配的结果距离数学期望越分散。
在MATLAB R 2012环境下开发了仿真器,所有机器人都具有相同的对于N种类型任务的感知与执行能力。个体机器人通过局部观察将任务类型存储在长度为h的历史窗口内,由于机器人没有关于任务数量的全局知识｛M1,…,MN｝,它使用历史窗口收集的局部观察｛m1,…,mN｝来估算转移函数的值:
实验1中历史窗口h=50,任务类型数量N=3,任务类型集合I1=｛i|R,G,B｝,任务的初始数量设置为(MR,MG,MB)=(25,15,5),群集规模n=30。以在时刻t处于任务状态i的机器人个数n′i占群集个数的即时比例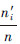 
作为任务分配描述符的实验值,将其在10次实验中的平均值用Fi(t)表示。结果由图3a)所示,其中每隔100 s绘制一个误差棒,表示10次实验的标准差。此后群集规模n=120,其余参数不变,结果由图3b)所示。从图3a)、图3b)可以看出Fi(t)的值围绕在由定理1给出的其理论值Pi(t)周围。比较图3a)与图3b)可知,当n=120时曲线误差幅度小于n=30时的幅度。图4a)与图4b)中带星号连线表示Fi(t)的统计规律,直方图表示 
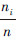的理论分布，误差棒表示10次实验的标准差。由图4可知当n=120与n=30时Fi(t)统计分布曲线均与表示其理论二项分布 
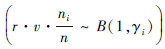的直方图吻合。但是n=120时方差小于n=30的方差,所以图4b)中代表任务分配结果的Fi(t)统计分布较为集中在数学期望附近,在图4a)中分布较分散,因此图3b)中曲线的抖动小于图3a)。正如推论3所述,规模越大,分配误差越小。
 |
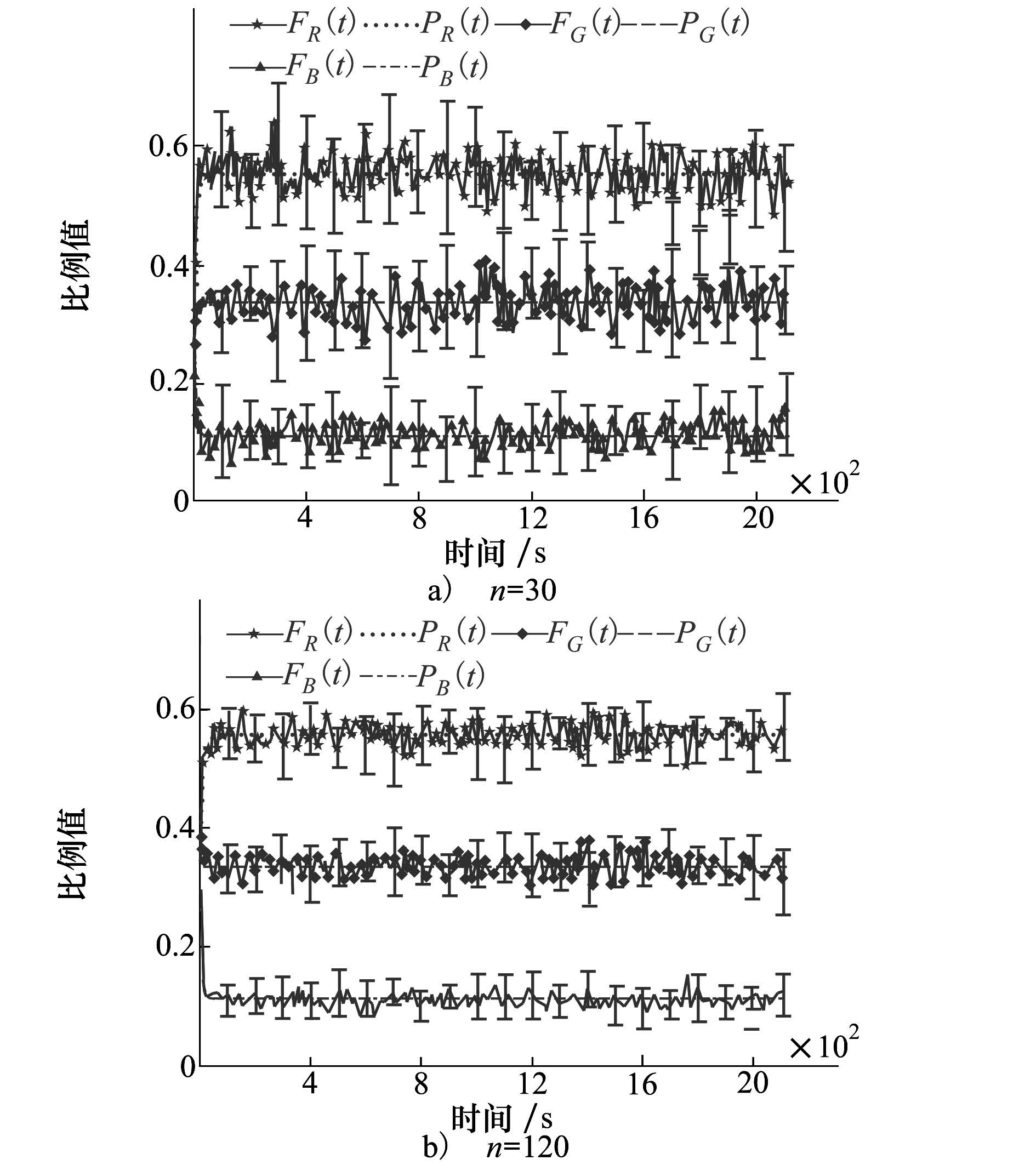| 图 3 FR(t),FG(t),FB(t)与PR(t),PG(t),PB(t)的值 |
 |
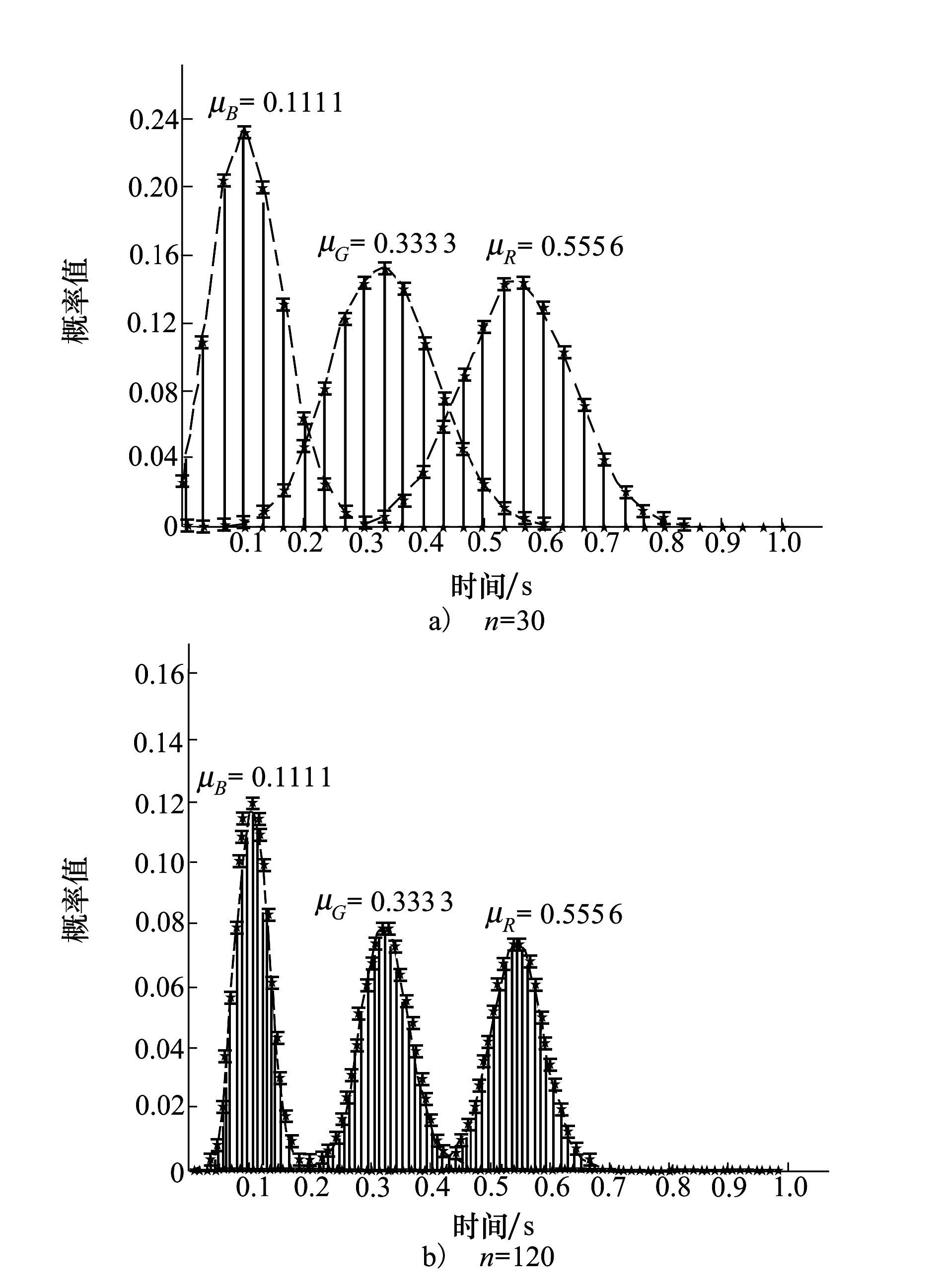| 图 4 任务类型数为3时Fi(t)的统计规律和理论分布 |
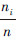的理论分布。由图5可知Fi(t)的统计分布曲线与二项分布的直方图吻合。由5a)与5b)2幅子图可知,统计分布曲线有相同期望值。但是n=120时方差小于n=30的方差,故Fi(t)统计分布较为集中在数学期望附近。此组实验进一步证明了推论2,推论3的正确性,即群集机器人任务分配结果的数学期望与规模无关,方差与规模反比。
 |
| 图 5 任务类型数为6时Fi(t)的统计规律和理论分布 |
本文的研究目的是提供除了物理实验，仿真，统计物理模型之外的一种新的基于二维马尔可夫动态系统中拟生灭过程的群集机器人任务分配模型，进行了系统行为的宏观分析与预测。它对任务类型数没有限制，提供了更好的系统性能分析结果，发现了群集任务分配服从二项分布这个统计规律，综合定性与定量分析方法得出所涌现的群集分配行为的正面效应是二项分布的数学期望，负面效应是其方差，和增加系统规模可以减小方差这个结论。仿真结果说明了新模型中预测与分析的正确性和可靠性。
| [1] | Correll N, Martinoli A. Modeling and Designing Self-Organized Aggregation in a Swarm of Miniature Robots[J]. International Journal of Robotics Research, 2011, 30(5): 615-626 |
| Click to display the text | |
| [2] | Kernbach S, Hbe D, Kernbach O, et al. Adaptive Collective Decision-Making in Limited Robot Swarms without Communication[J]. The International Journal of Robotics Research, 2013, 32(1): 35-55 |
| Click to display the text | |
| [3] | Hamann H, Wrn H. A Framework of Space-Time Continuous Models for Algorithm Design in Swarm Robotics[J]. Swarm Intelligence, 2008, 2(2): 209-239 |
| Click to display the text | |
| [4] | Massink M, Brambilla M, Latella P, et al. On the Use of Bio-PEPA for Modelling and Analysing Collective Behaviours in Swarm Robotics[J]. Swarm Intelligence, 2013, 7(2): 201-228 |
| Click to display the text | |
| [5] | Lerman K, Jones C, Galstyan A, et al. Analysis of Dynamic Task Allocation in Multi-Robot Systems[J]. The International Journal of Robotics Research, 2006, 25(3): 225-241 |
| Click to display the text | |
| [6] | Zhou J, Mu D, Yang F S, et al, A Distributed Approach to Load Balance for Multi-Robot Task Allocation[C]//Proceedings of the IEEE International Conference on Mechatronics and Automation, 2014: 612-617 |
| [7] | Zhou J, Mu D, Yang F S, et al, Labor Division for Swarm Robotic Systems with Arbitrary Finite Number of Task Types[C]//Proceedings of the IEEE International Conference on Information and Automation, 2014: 1113-1118 |
| Click to display the text | |
| [8] | Latouche G, Ramaswami V, Introduction to Matrix Analytic Methods in Stochastic Modeling[M]. 3600 University City Science Center, Philadelphia, PA, Society for Industrial and Applied Mathematics, 1999 |
| [9] | Neuts M. F., Matrix-Geometric Solutions in Stochastic Models[M]. Baltimore, Maryland, The John Hopkins University Press, 1981 |