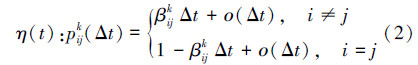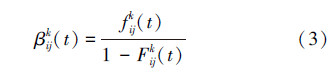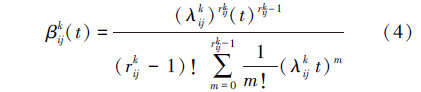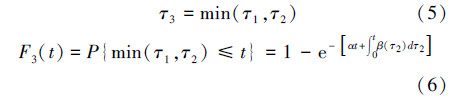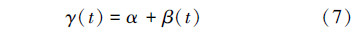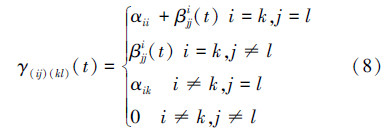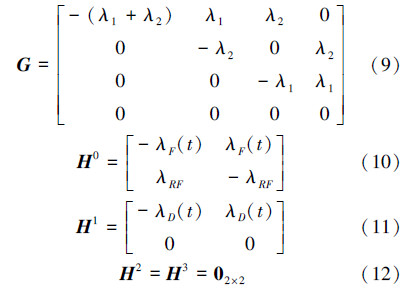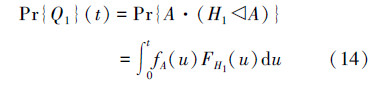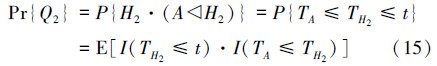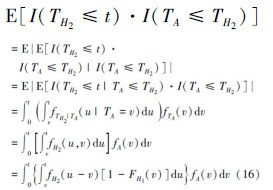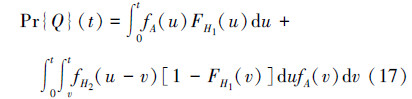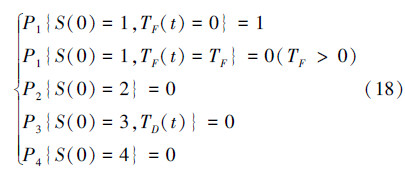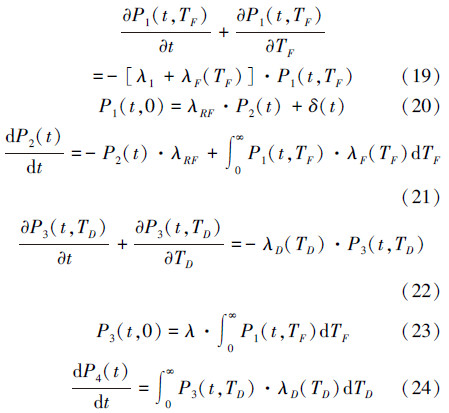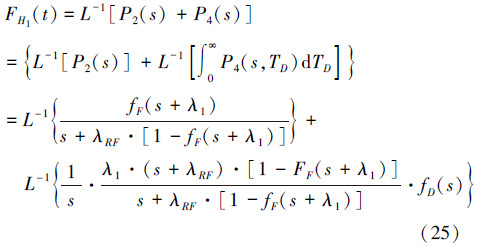传感器故障常会导致复杂动态过程中控制、监测、显示等功能的失效。为了提高传感器系统的可靠性,系统设计常采用硬件余度、解析余度以及两者结合的混合余度技术,对传感器故障进行实时诊断,并在故障情况下重构传感器的测量信号。因此,针对混合余度系统的可靠性建模与分析能够定量评价容错方法的性能,具有重要的研究意义。而混合余度的应用为系统引入了复杂的动态特性,主要带来了以下2个问题:
1)不完全故障诊断。由于传感器测量噪声与解析模型不确定性的影响,不完全的故障诊断会导致系统停留在某故障状态,从而降低系统的可靠性。
2)故障的时序性。系统中解析余度的作用通常为辅助故障诊断或作为故障安全输出信号。当解析余度先于硬件余度故障,则上述功能失效。因此,系统故障不仅取决于各余度的故障是否发生,也与解析余度与硬件余度的故障时序相关。
目前,故障诊断过程的可靠性建模通常只考虑误检与漏检概率,将故障诊断过程假设为可靠性元件进行处理,不能充分反映故障诊断的动态特性,也无法计算系统中间故障状态的概率[2]。文献[3, 4]中采用马尔可夫过程建立了故障诊断过程的动态模型,但该模型只适用于无记忆性的单样本故障诊断方法,需要进一步推广从而适用于常见的多样本检测方法。
故障时序性的分析方法则主要包括Markov过程法[5]、Petri网[6]以及代数模型[7, 8]等。Markov过程法只适用于指数寿命分布,且当系统状态数过多时,不易计算求解;Petri网方法在图形表现和计算求解上有时过于复杂;而代数模型方法能够将描述故障时序性的动态逻辑门转化为简练的代数逻辑,并且适用于任意故障时间分布,具有较好的应用前景。
针对以上情况,本文对文献[4]中的可靠性模型进行扩展,建立了适用性更广的集成半马尔可夫过程模型;并且研究了模型的定量概率求解方法,提出了一种代数模型与补充变量法结合(AMSV)的分析方法。
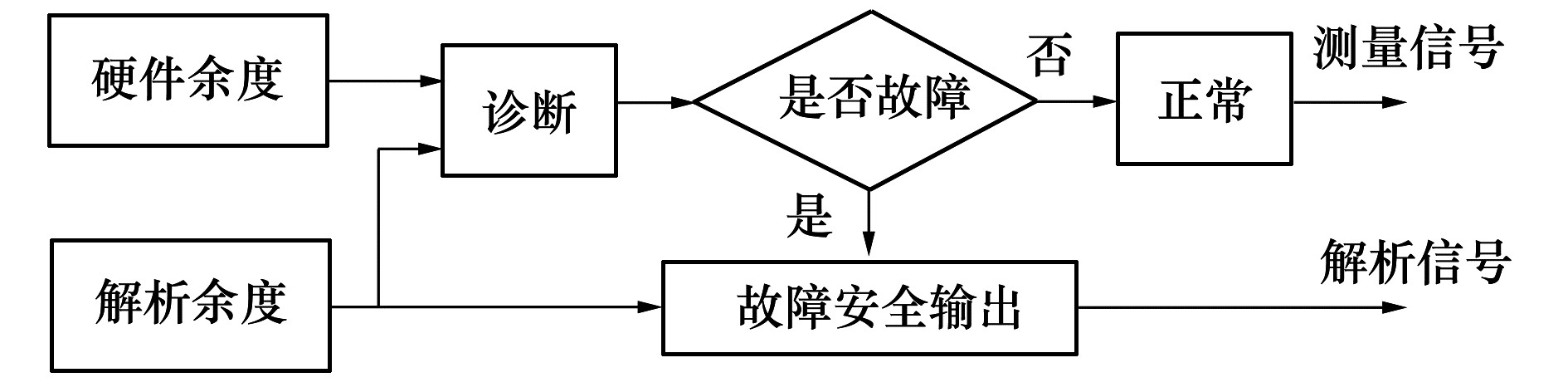
1 研究对象不失一般性,本文的研究对象选取单硬件余度加解析余度的混合系统。余度配置及余度管理如图 1所示。
 |
| 图 1 混合余度系统配置与余度管理示意图 |
系统的余度管理方案为:通过故障检测方法对解析余度与硬件余度的差值进行实时检验,实现对硬件余度的监控;当差值超过检测阈值时,硬件余度诊断为故障,系统输出切换为解析信号,实现故障下的安全输出。
2 集成半马尔可夫模型的建立 2.1 故障过程与诊断过程的建模混合余度系统的行为可分为元件故障过程与故障诊断过程,分别采用随机过程ζ(t)与η(t)进行建模描述。
传感器元件通常为电子设备,寿命满足指数分布,因此,ζ(t)为时间齐次马尔可夫过程。定义ζ(t)的状态空间为S1={0,1,…,N1},S1包括了系统的正常状态(状态0)和所有可能的故障状态(状态1到N1)。对于充分小的Δt>0,状态i到j的转移概率pij(i,j∈S1)为:
式中:αij为ζ(t)的转移率,ο(Δt)为Δt的高阶无穷项。ζ(t)的转移率矩阵为G=[±αij]N1×N1。
故障诊断过程模型为描述诊断结果的条件随机过程η(t),η(t)的状态以一定的随机时延和误差概率跟踪实际故障状态ζ(t)。定义η(t)的状态空间为S2={0,1,…,N2},对于充分小的Δt>0,状态i到j的转移概率pijk (i,j∈S2)为
βijk 代表给定ζ(t)=k时η(t)的转移率。η(t)的转移率矩阵为Hk=[±βijk (t)]N2×N2(ζ(t)=k)。
2.2 模型参数的确定ζ(t)的转移率参数αij取决于元件的失效率λ,可以通过可靠性手册或生产制造厂商获取。η(t)的转移率参数βijk则取决于状态转移时延。
状态转移时延定义为:故障诊断过程保持某个状态,未发生状态转移的时间,记为τ。Fijk (t)和fijk (t)分别为τ的分布函数与概率密度函数。Fijk (t),fijk (t)与βijk(t)满足:
状态转移时延的分布规律可以通过故障诊断算法的Monte Carlo仿真确定[9],常见的多样本检验的状态转移时延τ满足Gamma分布Γ(r,λ),条件转移率的具体公式为:
当故障诊断方法为单样本检验等无后效性的方法时,条件转移率βijk (t)=λijk 为定常值,此时状态τ的分布为Gamma分布Γ(r,λ)的特例——指数分布。
2.3 集成模型的建立在ζ(t)与η(t)的基础之上,建立混合系统的模型φ(t)。φ(t)的转移率矩阵G=[γ(ij)(kl)](N1+1)×(N2+1)(i,k∈S1;j,l∈S2)由ζ(t)和η(t)的二元组合决定。转移率矩阵元素的具体分析计算如下:
1)ζ(t)与η(t)均不发生状态转移
设τi(i=1,2,3)分别为ζ(t)、η(t)和φ(t)的状态转移时延,Fi(t)为对应的分布函数,α、β(t)、γ(t)分别为对应的转移率,显然有:
由(3)式、(5)式、(6)式可知,
2) ζ(t)与η(t)其中之一发生状态转移时,φ(t)的转移率即为状态发生转移的过程的转移率。
3) 故障过程ζ(t)与诊断过程η(t)同时发生状态转移的概率较小,可以忽略不计,转移率为0。
综上可得,转移率的具体计算公式为:
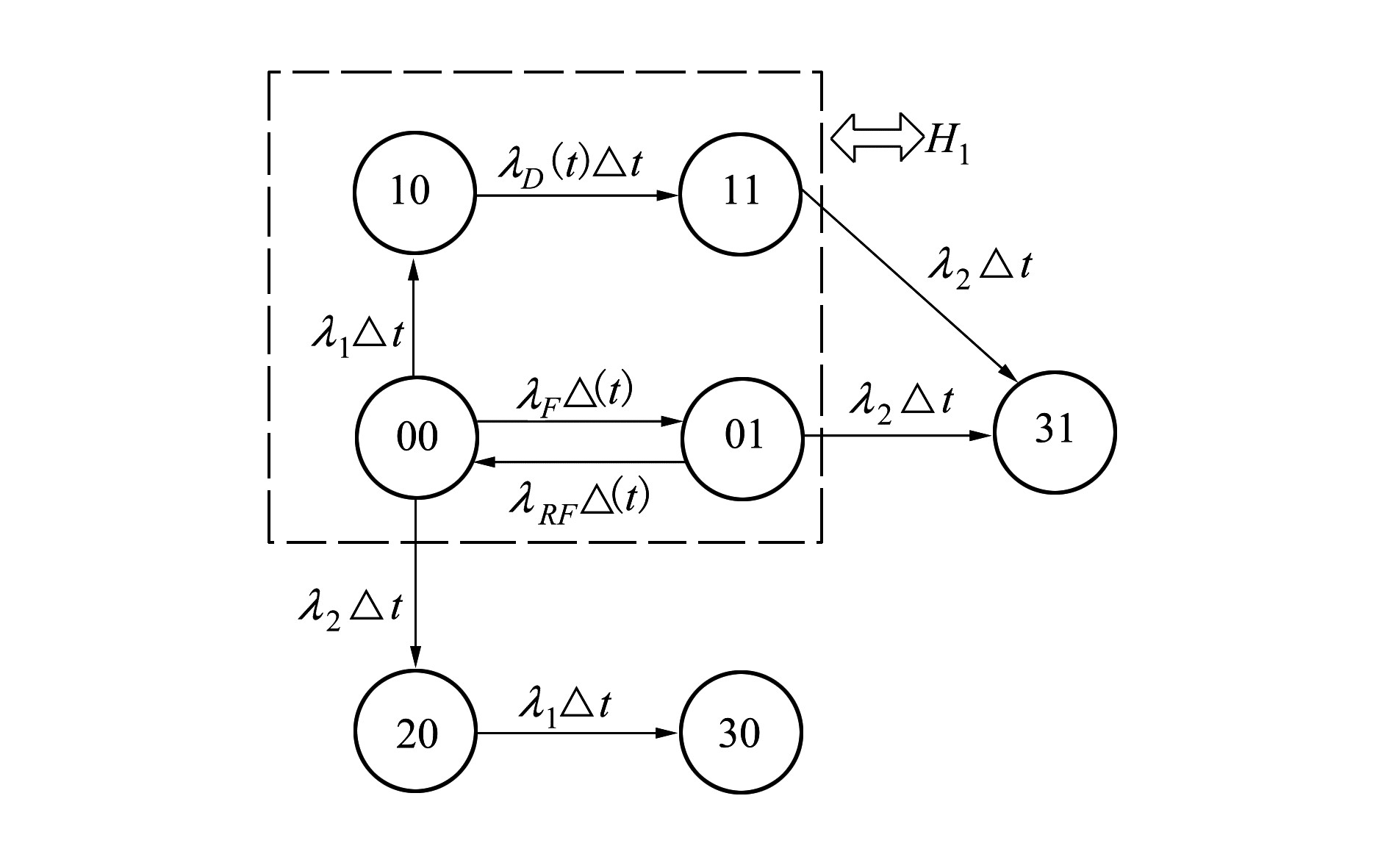
基于上述分析,假设混合余度系统为不可修系统,图 1系统对应的ζ(t)的状态空间S1={0,1,2,3},其中状态0代表解析余度与硬件余度均正常工作,状态1代表硬件余度故障,状态2代表解析余度故障,状态3代表两余度均发生故障。η(t)的状态空间S2={0,1},状态的定义与S1中相同。
由硬件和解析余度失效率λ1和λ2以及故障诊断的状态转移时延分布,可以确定ζ(t)和η(t)的转移率矩阵分别如下:
由(8)式~(12)式可得半马尔可夫模型如图 2所示,其中01状态到31状态转移率根据实际余度管理方案修正为λ2。
 |
| 图 2 集成半马尔可夫过程模型 |
由于Gamma分布的状态转移时延的条件转移率为时变的,状态转移概率不仅取决于当前时刻的系统停留状态,也与在当前状态的停留时间相关。因而,所建立的系统模型为半马尔可夫过程。
3 定量分析方法针对于第2节建立的半马尔可夫过程模型,补充变量法能够将其转化为广义马尔可夫过程进行求解[10],是一种有效的定量分析方法。然而,过程状态数的增加会导致复杂的求解过程。针对于此,所提出的AMSV方法将半马尔可夫过程转化为代数模型,代数模型中的故障模式对应的半马尔可夫过程状态数较小,采用补充变量法进行求解,系统总概率的计算则根据代数模型的定量公式对各模式结果进行综合。
为了反映故障诊断方法对系统总体性能的影响,系统可靠性的定量评价指标选取为安全度RS。安全度的定义为系统输出正确,或输出错误可检测的概率。
3.1 代数模型方法的应用代数模型方法的主要作用是将半马尔可夫模型转化为简练的代数逻辑形式。处理思路为:将事件定义为时间集合上取值为布尔代数值的函数变量,引入(在…之前)、Δ(同时发生)等时间算子描述时序逻辑,事件的定量概率根据变量的分布进行计算[7, 8]。
1) 半马尔可夫过程的转化
定义逻辑变量Q代表系统是否失效(0为正常,1为失效);A代表解析余度是否故障;变量H1代表解析余度故障前,硬件余度是否诊断为故障;H2分别代表解析余度故障后,硬件余度是否故障。半马尔可夫过程模型转化后的代数模型为:
式中,事件H1与图 2中虚线框所示的半马尔可夫子过程相关。
由(13)式可知,2个不相关故障模式分别为:
Q1=A·(H1◁A),硬件余度首先诊断为故障,然后解析余度故障;Q2=H2·(A◁H2),解析余度先于硬件余度故障,然后硬件余度子系统故障。
2) 故障模式的定量概率计算
定义Fi(t)和fi(t)为各事件的分布函数与概率密度函数(i=A,H1,H2)。故障模式Q1中,硬件余度先于解析余度故障,因此FH1(t)与FA(t)相互独立。模式Q1的失效概率公式为:
故障模式Q2中,FH2(t)与FA(t)相关,(14)式的形式不再适用,失效概率公式具体推导如下:
设TA和TH2分别为A和H2的故障发生时间。
式中,I(·)为指示函数。
由全期望公式E[X]=E[E[X|Y]]可得,故障模式Q1与Q2相互独立,所以有
H2和A分别满足失效率为λ1和λ2的指数分布。H1的分布则根据对应的半马尔可夫过程,通过补充变量法求解。
3.2 补充变量法的应用补充变量法的主要作用是针对约简后的半马尔可夫模型进行求解(即H1对应的半马尔可夫子过程,如图 3所示)。求解过程如下:
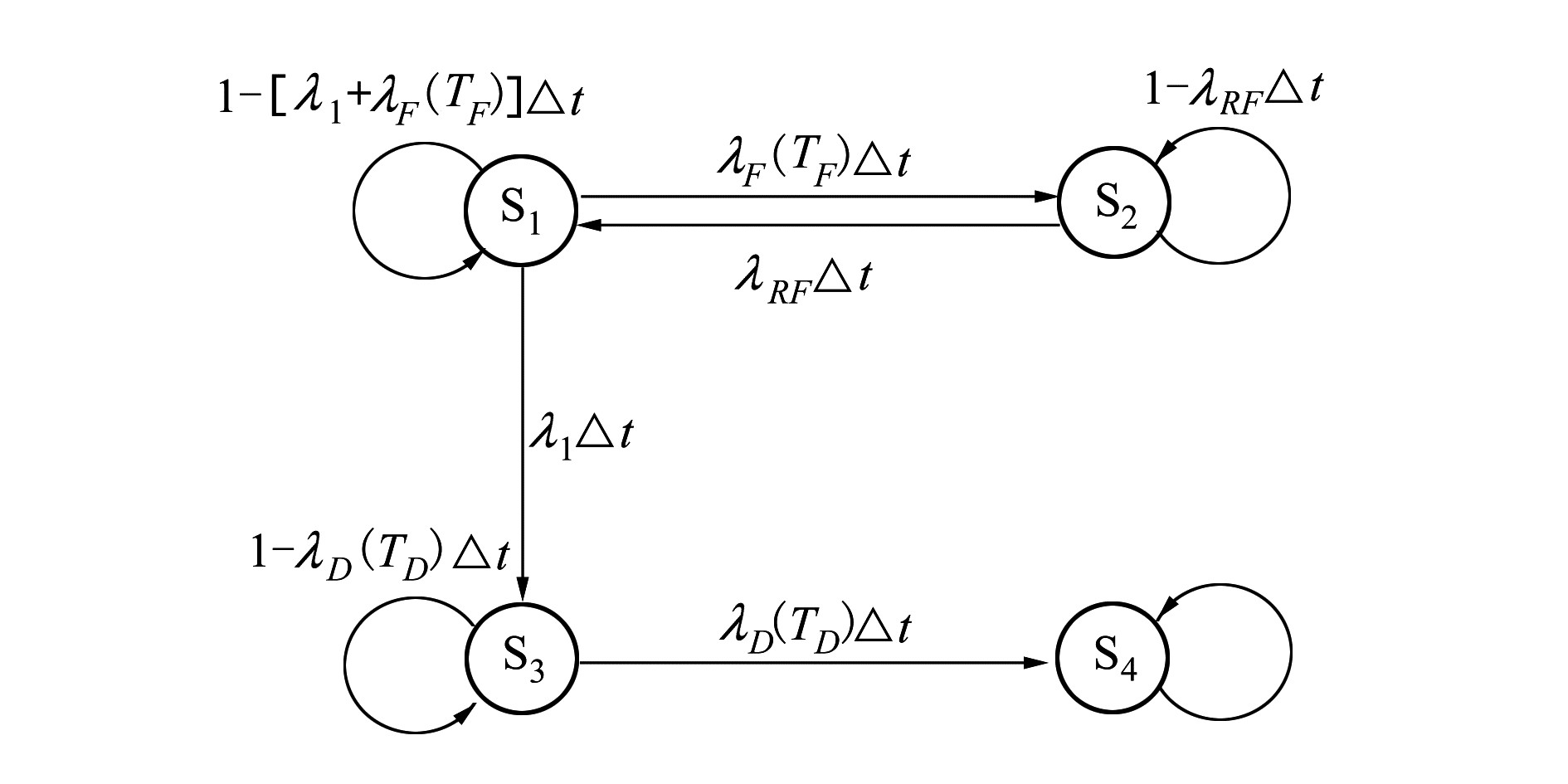 |
| 图 3 H1对应的半马尔可夫模型 |
定义TF(t)、TD(t)分别为t时刻元件无故障和发生故障情况下诊断算法运行的时间。转化后的广义马尔可夫过程表示为{S(t),TF(t),TD(t),t≥0}。
状态{S(t)=1,TF(t)=TF}代表系统元件正常工作,故障诊断运行时间为TF并且无虚警;状态{S(t)=2}代表系统正常工作并且故障诊断为误检状态;状态{S(t)=3,TD(t)=TD}表示系统元件故障,诊断方法运行了时间TD且未检测到故障;状态{S(t)=4}表示故障已经得到检测。f(·)、F(·)分别为状态转移时延的概率密度函数和分布函数。
系统初始条件为:
系统状态概率方程组如下:
通过对(19)式~(24)式进行L变换,结合初始条件(18)式,即可求解得到各状态的概率公式。H1的分布函数FH1(t)为状态S2与S4的概率之和。计算公式为:
至此,H1、H2以及A的分布均已知,根据(17)式采用数值积分即可求解得到系统的失效概率F(t)=Pr{Q}(t)以及安全度RS(t)=1-F(t)。
4 算例分析 4.1 与补充变量法的对比验证设定系统硬件余度失效率λ1=5×10-5/h,解析余度失效率λ2=2×10-4/h。λD(t)对应的状态时延τD~Γ(10,165.94),λF(t)对应的状态时延τF~Γ(2,10-4),λRF(t)对应的状态转移时延τRF~Γ(1,115.13)。
分别采用补充变量法(SV)和本文所提的AMSV法进行定量概率的求解,SV方法的求解过程与3.2节类似,不再重复给出。计算结果如图 4所示。图中所示的AMSV与SV 2种方法计算得到的系统失效概率F(t)曲线基本重合,表明安全度计算结果相同,验证了所提出的AMSV方法的正确性。
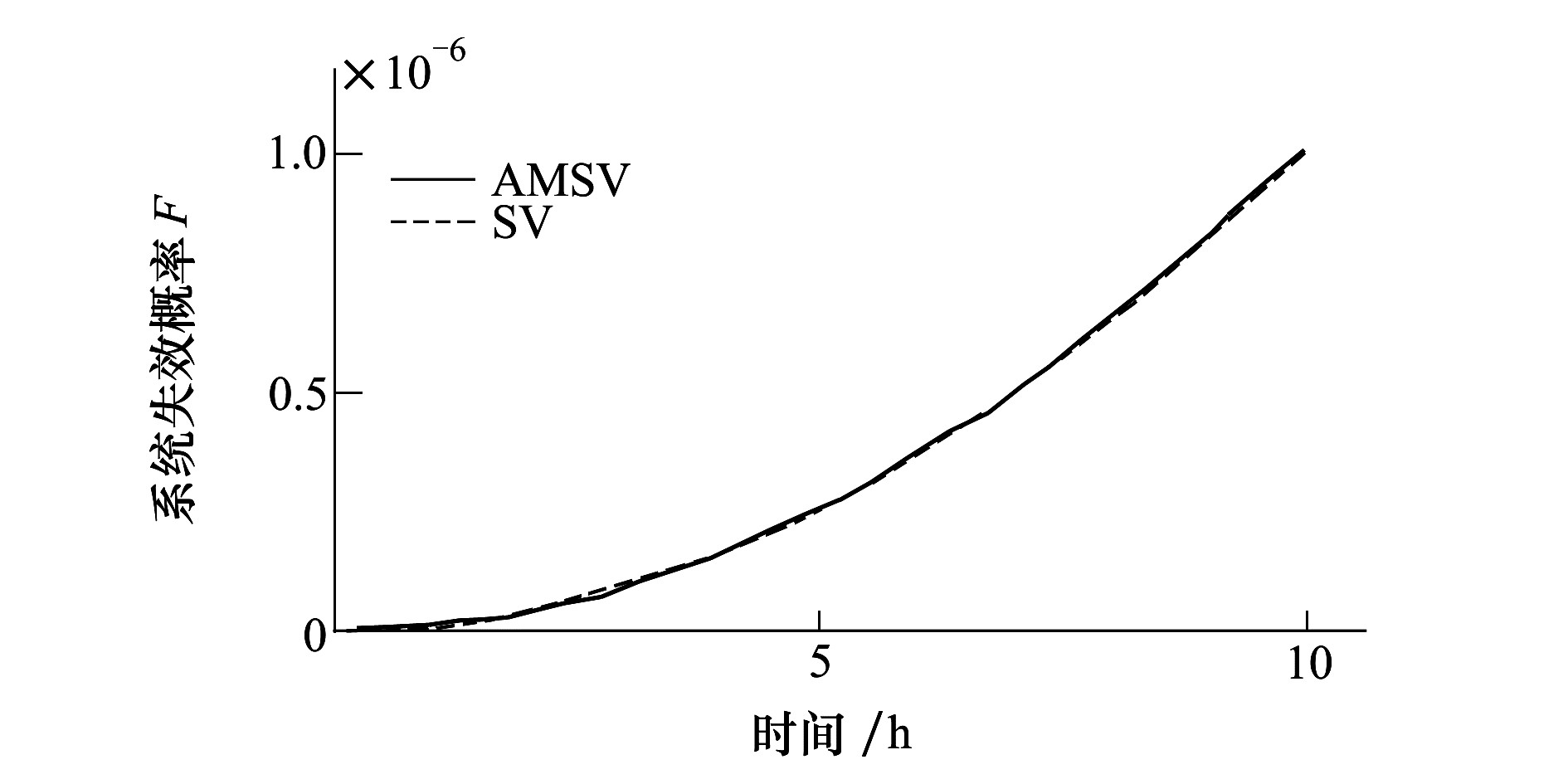 |
| 图 4 AMSV与SV 2种方法的对比 |
比较2种方法,AMSV方法只需针对状态数为4的半马尔可夫过程进行求解,而SV方法的分析对象状态数为7,AMSV方法减少了复杂的L变换运算,求解过程更为便捷。同时由公式(17)可知,AMSV方法对于H1、H2、A的分布没有特定限制,通用性更强。而当上述变量不满足指数分布时,SV方法求解需要引入更多补充变量,定量概率计算的复杂度将大大增加。
4.2 与时齐马尔可夫过程法的对比验证当系统故障诊断采用单样本检验等无后效性方法时,状态时延服从指数分布。系统模型简化为文献[4]提出的时齐马尔可夫过程,φ(t)的转移率矩阵G为定常矩阵。当进一步假设系统所采用的为完全故障诊断时,模型可以进一步简化。时齐马尔可夫过程的常用求解方法为如(26)式所示的状态微分方程法。
设定单样本检验的状态时延指数分布参数分别为λD=103,λF=10-4,λRF=5×102,其余参数设置与4.1节相同。完全故障诊断情况下,状态时延分布参数λD=λF=λRF=0,采用状态微分方程对2种情况分别进行求解,并与AMSV法进行对比,如图 5所示。
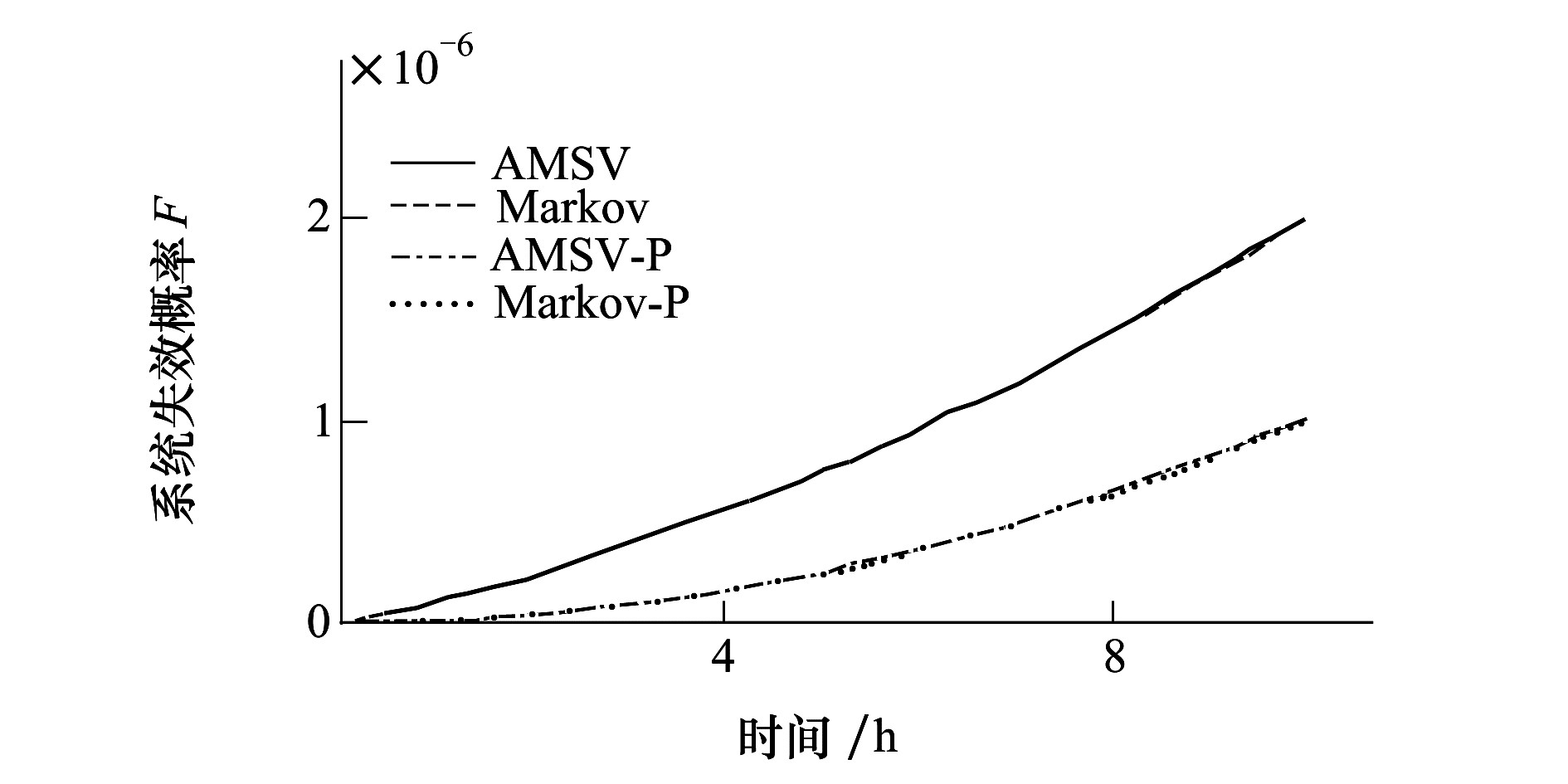 |
| 图 5 概率微分方程与AMSV的计算结果对比(AMSV与Markov曲线为单样本检验下的对比, AMSV-P与Markov-P曲线为完全故障诊断下的对比) |
图 5中AMSV与概率微分方程的计算结果相同,进一步验证了AMSV方法的正确性,也表明单样本检验以及完全故障诊断的时齐马尔可夫过程模型是集成半马尔可夫模型的特例,验证了所提出的模型的通用性。而不完全故障诊断(AMSV和Markov曲线所示)与完全故障诊断(AMSV-P和Markov-P曲线所示)的系统失效概率的明显差别,也表明故障诊断建模的必要性。
5 结 论本文针对采用故障诊断以及信息重构容错方法的混合余度系统进行了可靠性的建模与分析,并通过算例验证了AMSV定量分析方法。所建立的半马尔可夫模型的适用范围更为广泛,能够对元件故障过程和单样本、多样本故障诊断过程进行准确描述。所提出的AMSV方法适用于任意的元件寿命分布且求解过程更为简便。
| [1] | 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社, 2006:301-308 Cao Jinhua, Cheng Kan. Introduction to the Mathematics of Reliability[M]. Beijing, Higher Education Press, 2006:301-308(in Chinese) |
| [2] | Myers A, Rauzy A. Efficient Reliability Assessment of Redundant Systems Subject to Imperfect Fault Coverage Using Binary Decision Diagrams[J]. IEEE Trans on Reliability, 2008, 57(2):336-348 |
| Click to display the text | |
| [3] | 高飞,张洪钺.带马尔可夫参数容错控制系统的可靠性分析[J].北京航空航天大学学报, 2007, 33(3):302-306 Gao Fei, Zhang Hongyue. Reliability of Fault Tolerant Control System with Markovian Parameters[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3):302-306(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [4] | Li H, Zhao Q, Yang Z. Reliability Modeling of Fault Tolerant Control Systems[J]. International Journal of Applied Mathematics and Computer Science, 2007, 17(4):491-504 |
| Click to display the text | |
| [5] | 张竞凯,章卫国,刘小雄,等.基于代数模型的飞控计算机可靠性分析方法[J].北京航空航天大学学报,2014,40(2):262-267 Zhang Jingkai, Zhang Weiguo, Liu Xiaoxiong, et al. Reliability Analysis Based on Algebraic Model for Flight Control Computers[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2):262-267(in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [6] | 孙晓哲,李卫琪,陈宗基.飞控计算机系统分层混合可靠性建模方法[J].上海交通大学学报,2011,45(2):277-283 Sun Xiaozhe, Li Weiqi, Chen Zongji. Hierarchical Hybrid Reliability Modeling Method for Flight Control Computer System[J]. Journal of Shanghai Jiaotong University, 2011, 45(2):277-283(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [7] | Merle G,Roussel J M,Lesage J J, et al.Algebraic Expression of the Structure Function of a Subclass of Dynamic Fault Trees[C]//Proceedings of the 2nd IFAC Workshop on Dependable Control of Discrete Systems,2009:129-134 |
| Click to display the text | |
| [8] | Merle G,Roussel J M,Lesage J J,et al.Analytical Calculation of Failure Probabilities in Dynamic Fault Trees Including Spare Gates[C]//European Safety and Reliability Conference,2010 |
| Click to display the text | |
| [9] | 王社伟,张洪钺,陶军.基于半马尔可夫过程的容错导航系统可靠性分析[J].航天控制, 2006, 24(2):84-87 Wang Shewei, Zhang Hongyue, Tao Jun. Reliability Analysis of Fault Tolerant Navigation System Based on Semi-Markov Process[J]. Aerospace Control, 2006, 24(2):84-87(in Chinese) |
| Cited By in Cnki (7) | Click to display the text | |
| [10] | 李军,刘君华.多传感器融合系统的可靠性模型研究[J].西安交通大学学报, 2004, 38(8):775-778 Li Jun, Liu Junhua. Study of Reliability Model for the Multi Sensor Fusion System[J]. Journal of Xi'an Jiaotong University, 2004, 38(8):775-778(in Chinese) |
| Cited By in Cnki (14) | Click to display the text |