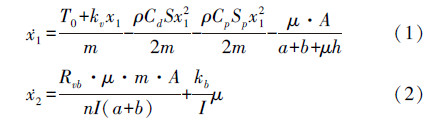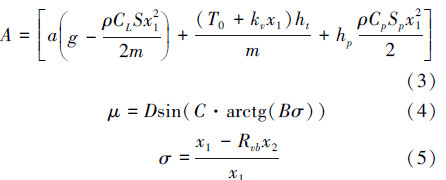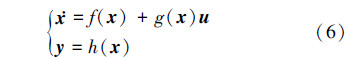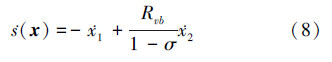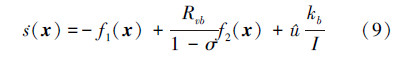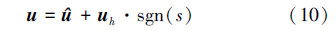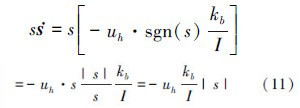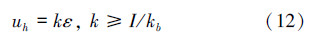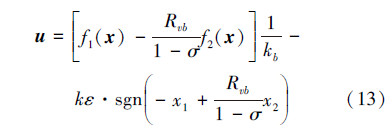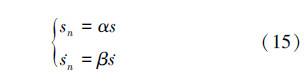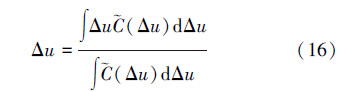防滑刹车系统是现代飞机的重要组成部分,它在飞机起飞、降落、滑行中对保证飞机安全起到至关重要的作用,所以随着航空事业的发展,飞机对刹车控制有着更高的要求。
飞机防滑刹车是一个复杂多变量非线性系统,系统参数变化和外界扰动会极大地影响精确控制的实现。采用鲁棒非线性控制理论可提高其控制品质。
文献[1]建立了飞机防滑刹车系统关于飞机速度的运动模型,文献[2]提出了刹车系统的滑模变结构控制方法,并验证了其正确性及有效性,文献[3]针对刹车控制系统的非线性和不确定性采用输入输出反馈线性化方法对原有控制算法进行改进。
本文将飞机滑移率作为控制对象,针对高度非线性的飞机防滑刹车系统,设计模糊滑模变结构控制器,将滑模变结构控制器的切换函数及其导数作为模糊控制器的输入,输出附加控制量,削弱滑模变结构控制固有抖振,提高了防滑刹车系统的控制性能。
1 飞机防滑刹车系统原理飞机刹车制动是飞机轮胎与地面相互作用的过程,飞机依靠两者之间的结合力进行制动。在飞机质量一定的条件下,结合系数μ是影响结合力大小的因素。结合系数μ受滑移率、轮胎新旧、轮胎类型、跑道表面状况等的众多因素影响。其中,滑移率σ对我们的研究有最重要的意义[4]。
要使飞机在尽可能短的距离内刹停,必须尽量使结合系数μ保持在最大值。最大结合系数μm对应最佳滑移率σp,因此,飞机防滑刹车系统通常将机轮的滑移率σ作为控制目标,使滑移率在最佳滑移率σp附近浮动。
2 飞机防滑刹车系统非线性模型飞机防滑刹车是一个复杂的非线性系统,为了简化系统模型,只考虑飞机的航向、垂直及俯仰方向上运动,假设所有受刹机轮的防滑机构拥有相同性能。本文采用文献[1]的方法,飞机的速度等于自由滚动的前轮速度。飞机刹车系统非线性模型如下:
式中
符号定义参见文献[1]。
3 滑模控制器设计考虑如下非线性系统:
式中,x是状态向量,u是控制量,y是输出向量,g(x)、h(x)是具有相应维数的充分光滑函数。
3.1 滑模切换面设计对于飞机防滑刹车系统,(1)式、(2)式与(6)式的对应关系如下:
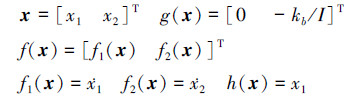
控制目标是当系统存在不确定性的情况下,调节刹车压力使滑移率快速跟踪选定数值。故根据滑移率公式(5)设计滑模切换面函数为
3.2 滑模控制律设计对(7)式微分得
即
式中: 是等效控制律,所以取控制律为
是等效控制律,所以取控制律为
由(7)式、(10)式得
取
则满足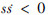 ,所以滑模切换面存在且可达。
,所以滑模切换面存在且可达。
因此由(10)式、(12)式得防滑刹车系统滑模控制律为
4 模糊控制器设计(10)式中uh·sgn(s)项含符号函数sgn(s),容易引起系统抖振。下面利用模糊集理论[5]确定附加控制。令
由(10)式可知,s>0时,Δu < 0;s < 0时,Δu>0。利用模糊集理论确定 ,以便使控制信号平滑。
将滑模切换函数s和它对时间的变化率规范化,假设
是模糊控制器的2个输入,Δu作为模糊控制器的输出,并将其模糊化为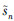 、
、 和Δuũ,定义sn和
和Δuũ,定义sn和 的语言值为PB,PS,ZE,NS,NB,Δu的语言值为PB,PM,PS,ZE,NS,NM,NB。
的语言值为PB,PS,ZE,NS,NB,Δu的语言值为PB,PM,PS,ZE,NS,NM,NB。
假设输入的模糊集为:
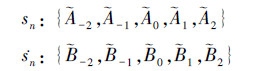
输出的模糊集为:
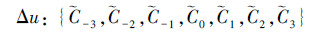
其对应的语言值为Ã-2=NB,Ã-1=NS,Ã0=ZE,Ã1=PS,Ã2=PB;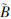 -2=NB,
-2=NB,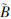 -1=NS,
-1=NS,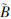 0=ZE,
0=ZE,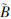 1=PS,
1=PS,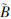 2=PB,
2=PB,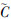 -3=NB,
-3=NB,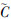 -2=NM,
-2=NM,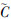 -1=NS,
-1=NS,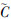 0=ZE,
0=ZE,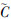 1=PS,
1=PS,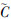 2=PM,
2=PM,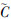 3=PB。
3=PB。
定义他们的隶属函数分别如图 1、图 2和图 3所示。
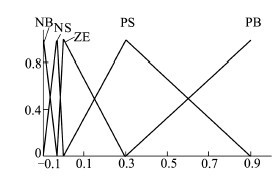 |
| 图 1 s的隶属函数 |
 |
图 2  的隶属函数 的隶属函数 |
 |
| 图 3 Δu的隶属函数 |
定义模糊控制规则如下表。
根据控制规则表以及MIN-MAX-重心法[6]可以将模糊控制器输出转化为精确的控制量
则系统控制信号为
其中Û由(9)式给出,k由(12)式给出,Δu由(16)式计算得出。
飞机防滑刹车系统模糊滑模变结构控制框图如图 4所示。
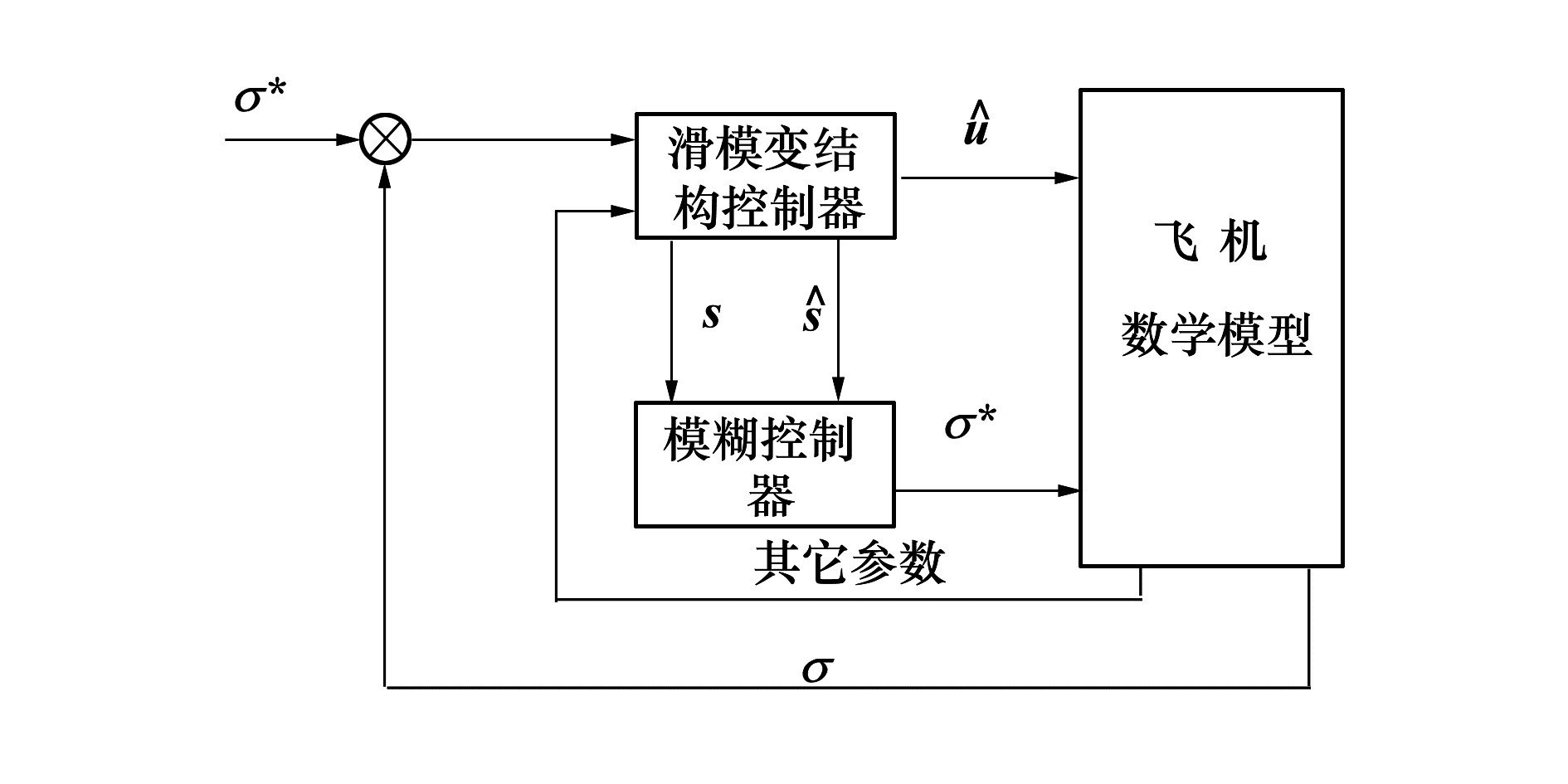 |
| 图 4 模糊滑模变结构控制框图 |
在MATLAB/Simulink环境下,建立飞机防滑刹车的模糊滑模变结构仿真模型,使用M语言编写滑模变结构控制器及模糊控制器。选定仿真初始状态:
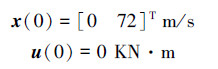
仿真设置防滑刹车控制器在1.5 s时开始运行,选择干跑道对模型进行仿真研究。
图 5是PBM偏压调节控制在干跑道上的仿真曲线。图 5a)是速度曲线,飞机速度下降不平稳,而且机轮速度的波动大。图 5b)的刹车压力曲线显示,在PBM控制律的作用下,飞机防滑刹车的作动机构输出的刹车压力波动大,这是飞机速度下降不平稳的原因。图 5c)是滑移率曲线,它的波动大,不能稳定在最佳值,且偏差逐渐增大。防滑刹车系统作用时间18.5 s,停止作用时飞机速度3 m/s。
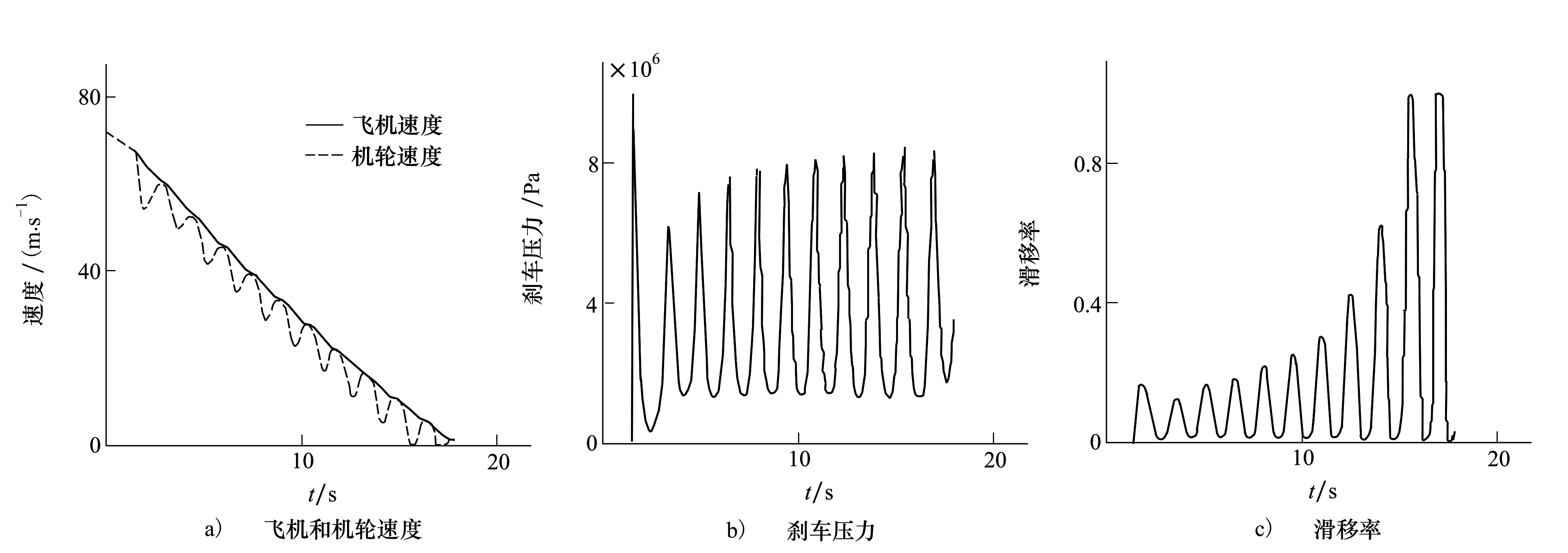 |
| 图 5 基于PBM的仿真结果 |
图 6是使用模糊滑模变结构控制的防滑刹车在干跑道上的仿真曲线。图 6a)和图 6b)分别为速度曲线和刹车压力曲线。在模糊滑模变结构控制作用下,刹车作动机构输出刹车压力平稳,飞机速度与机轮速度平缓下降,刹车全程无打滑。图 6c)的滑移率曲线表明,滑移率能较快到达并稳定在最佳值附近。防滑刹车系统作用时间16 s,停止作用时飞机速度2 m/s。
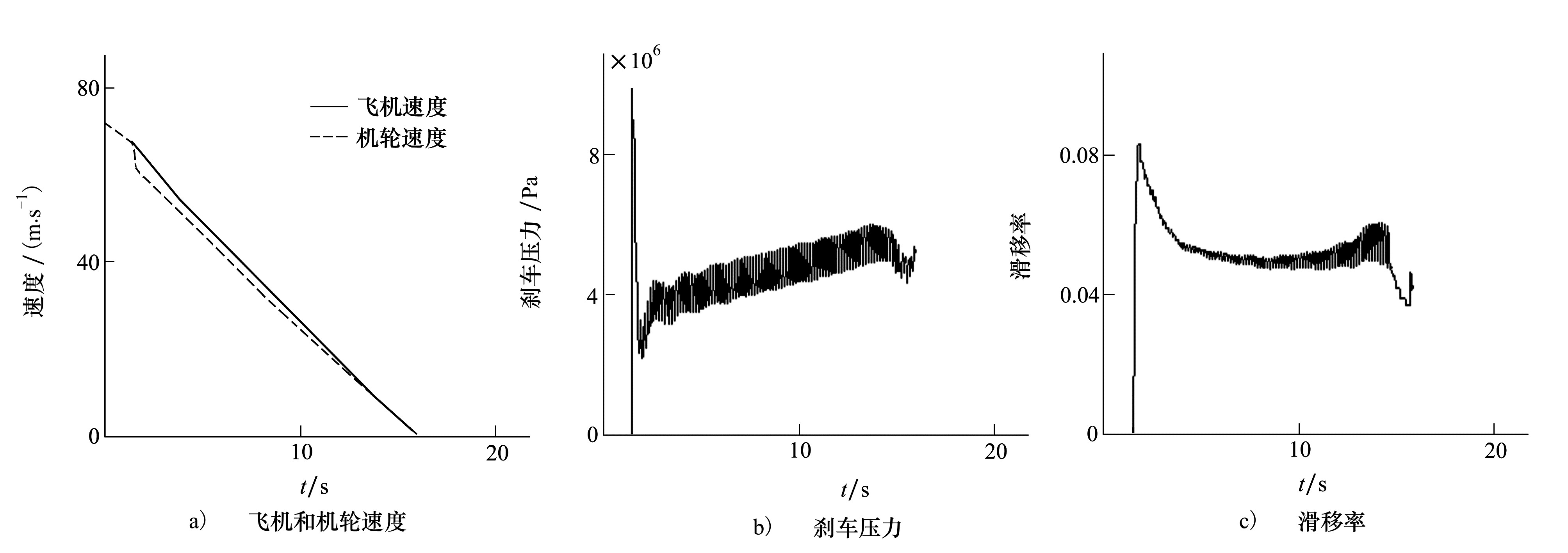 |
| 图 6 基于模糊滑模变结构控制的仿真结果 |
通过不同控制律的仿真结果,可以看出模糊滑模变结构控制能有效柔化防滑刹车系统的输出刹车压力,保持系统工作在最佳滑移率状态,提高刹车品质,使飞机的减速滑行更平缓。
6 结 论本文设计了一种滑模变结构控制与模糊控制相结合的防滑刹车控制方法,进行了仿真研究。在滑模变结构控制中通过模糊控制进行附加控制,不但保留了滑模控制的优点,而且有效抑制系统的抖振现象,柔化控制信号。仿真结果表明,系统能输出平滑的控制信号,保持最佳滑移率状态,使飞机刹车平缓,提高刹车效率。
| [1] | 李玉忍,马瑞卿,薛晶,等.飞机防滑刹车系统的变结构控制研究[J].西北工业大学学报, 2009, 26(6):752-755 Li Yuren, Ma Ruiqing, Xue Jing, et al. Improving Variable Structure Control of Aircraft Anti-Skid Brake System[J]. Journal of Northwestern Polytechnical University, 2009, 26(6):752-755(in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [2] | 李丰羽,焦宗夏.基于结合力模型的自适应飞机防滑刹车控制[J].北京航空航天大学学报, 2013,39(4):447-452 Li Fengyu, Jiao Zongxia. Adaptive Control for Aircraft Anti-Skid Braking System Based on Friction Force Model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4):447-452(in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [3] | 王纪森.非线性控制理论在防滑刹车系统中的应用研究[D].西安:西北工业大学, 2001 Wang Jisen. Nonlinear Control Theory and Its Application to Aircraft Antiskid Brake Systems[D]. Xi'an, Northwestern Polytechnical University, 2001(in Chinese) |
| Cited By in Cnki (54) | |
| [4] | Liang Bo, Li Yuren, Zhang Zhihui. Research on Simulation of Aircraft Electro-Hydrostatic Actuator Anti-Skid Braking System[J]. 2011 Third International Conference on Measuring Technology and Mechatronics Automation, 2011:78-82 |
| Click to display the text | |
| [5] | 王辉,孙悦.基于模糊免疫PID控制的飞机防滞刹车研究[J].计算机仿真, 2012, 29(4):43-48 Wang Hui, Sui Yue. Research on Aircraft Antiskid Braking System Based on Fuzzy Immune PID[J]. Computer Simulation, 2012, 29(4):43-48(in Chinese) |
| Cited By in Cnki (5) | Click to display the text | |
| [6] | 陈志梅,王贞艳,张井岗.滑模变结构控制理论及应用[M].北京:电子工业出版社,2012 Chen Zhimei, Wang Zhenyan, Zhang Jinggang. Theory and Application of Sliding Mode Variable Structure Control[M]. Beijing, Publishing House of Electronics Industry, 2012(in Chinese) |