攀爬机器人动力学建模与分析

王学军; 张帆

doi:10.13433/j.cnki.1003-8728.20200601

攀爬机器人动力学建模与分析

doi: 10.13433/j.cnki.1003-8728.20200601

王学军,
张帆

昆明理工大学机电工程学院, 云南省先进装备智能制造技术重点实验室, 云南省先进装备智能维护工程研究中心, 昆明 650500

基金项目:

国家重点研发计划项目 2017YFC1702503

国家自然科学基金项目 51565021

详细信息

作者简介:
王学军, 副教授, 硕士生导师, 研究方向为机器人动力学, km_wxj@kust.edu.cn

中图分类号: TH113
计量
- 文章访问数: 56
- HTML全文浏览量: 20
- PDF下载量: 34
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-31
- 刊出日期: 2023-01-25

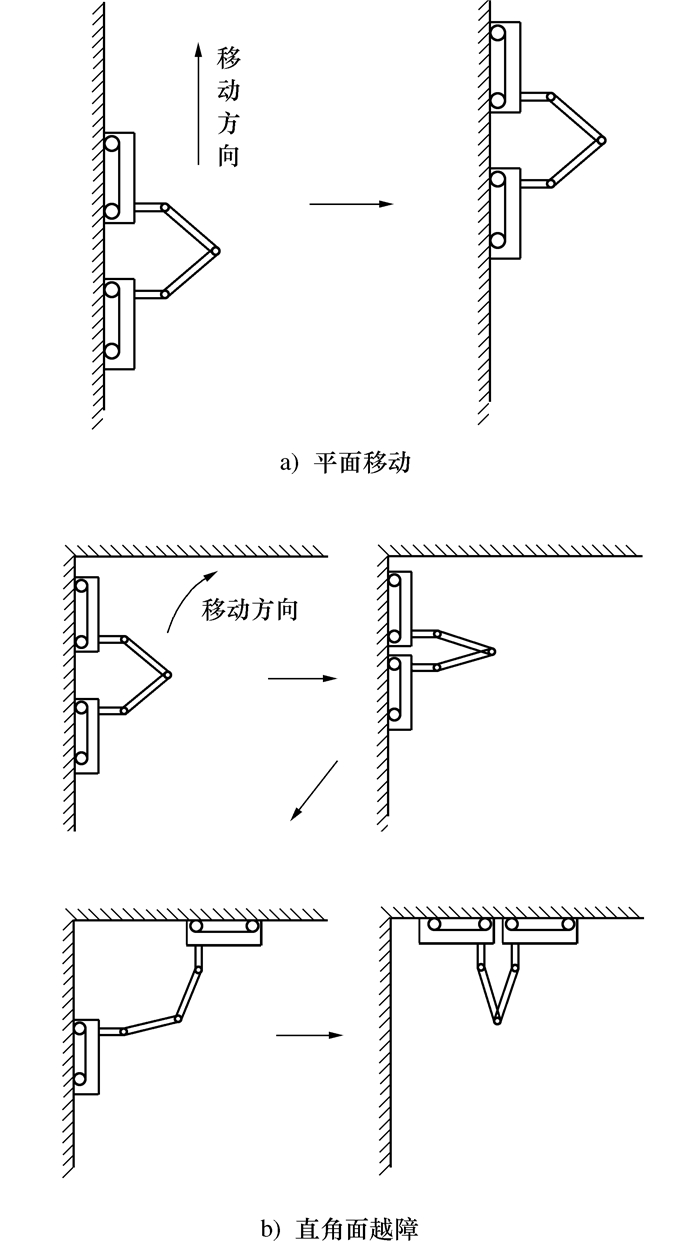
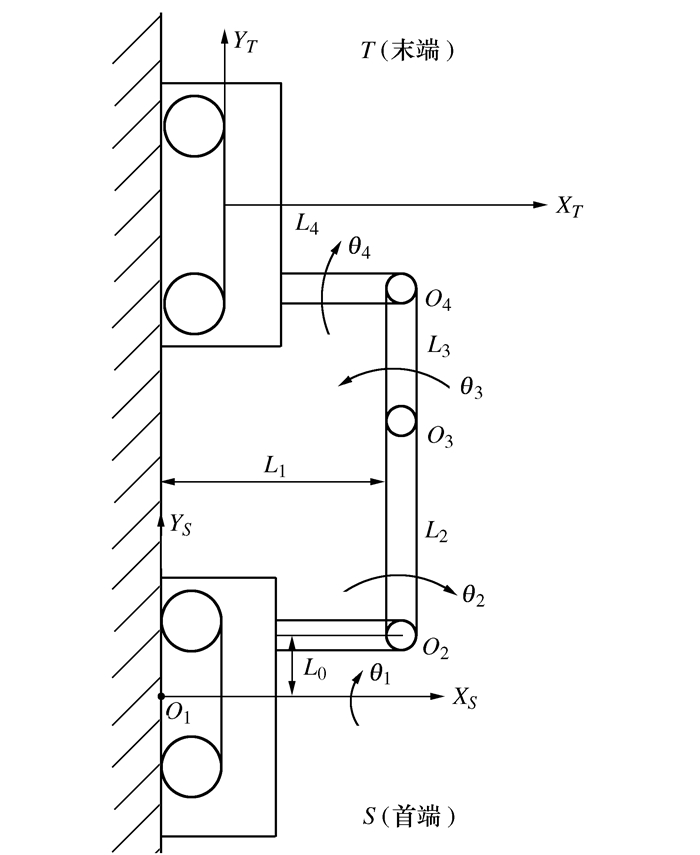
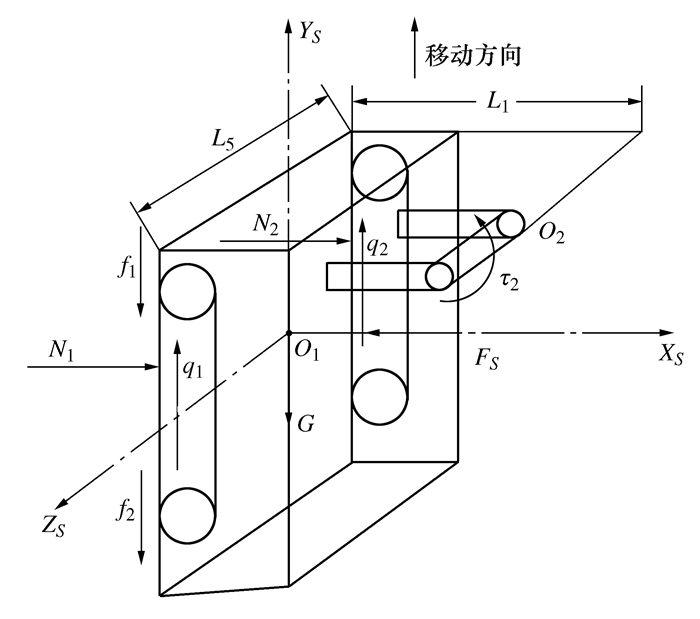
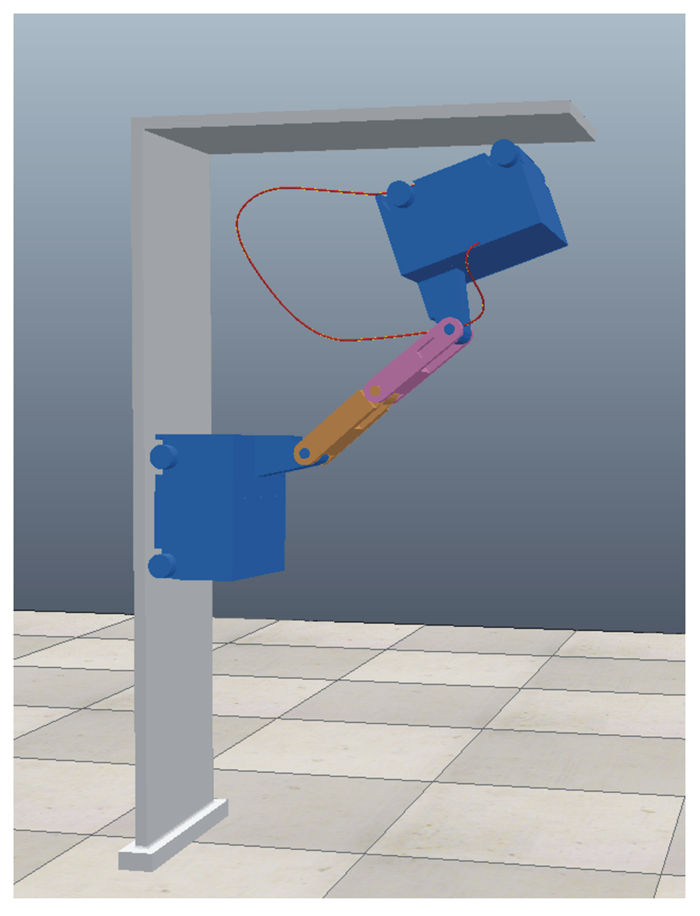
Dynamic Modeling and Analysis of Climbing Robot

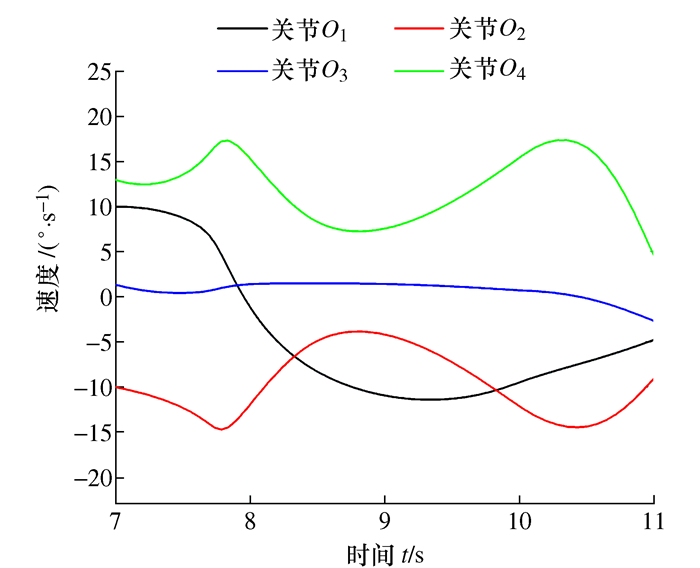
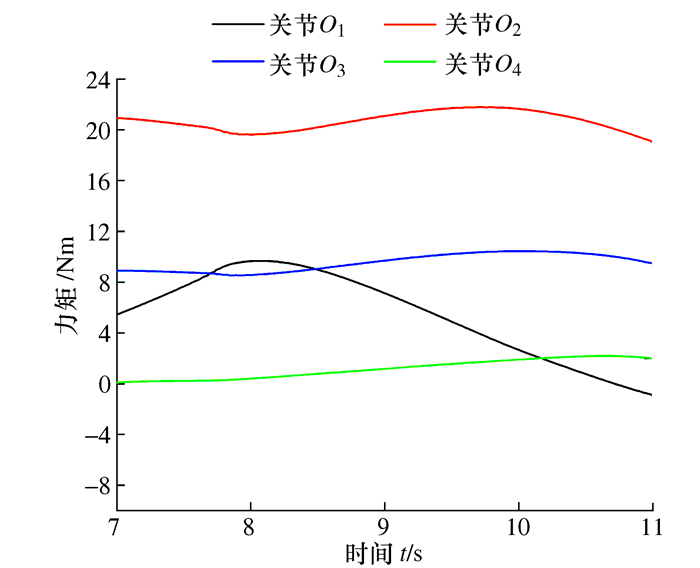
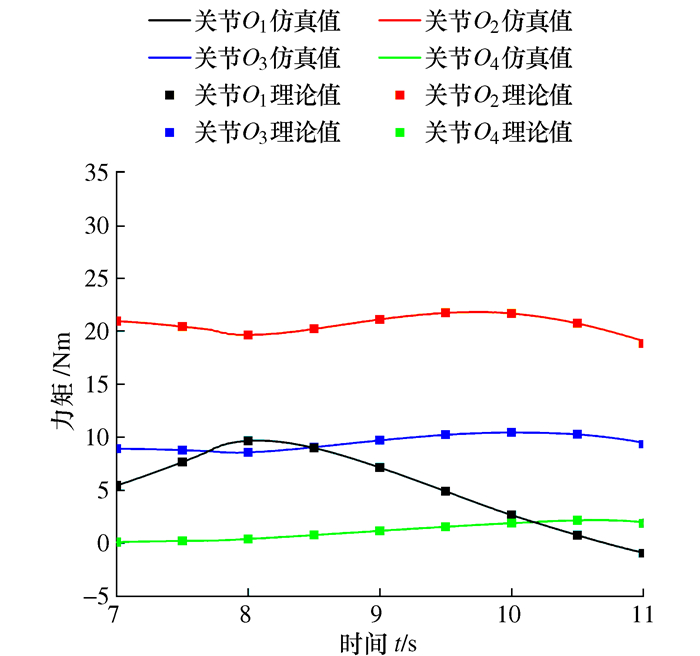
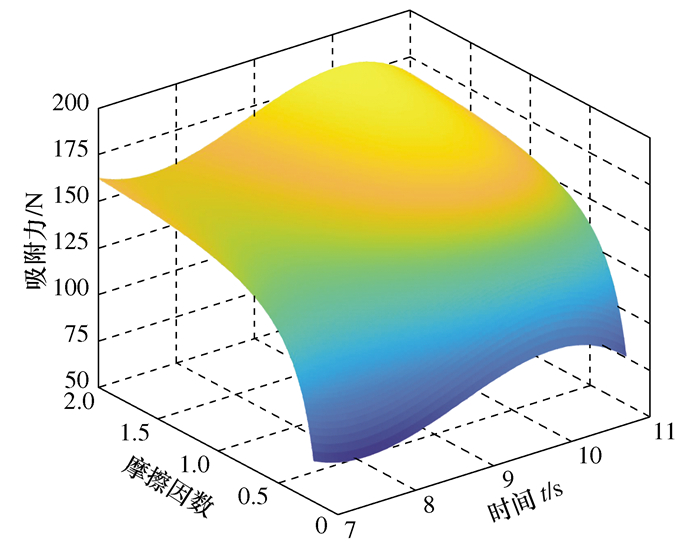
Yunnan Provincial Key Laboratory of Advanced Equipment Intelligent Manufacturing Technology, Yunnan Advanced Equipment Intelligent Maintenance Engineering Research Center, School of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China

摘要

摘要: 在越障运动过程中攀爬机器人动力学特性分析方法。通过指数积空间的形式推导得到了空间速度雅可比矩阵进而减少因微分求导而产生的奇点，基于李群李代数与旋量理论通过拉格朗日方程建立了物理意义明确、计算复杂度低的动力学方程，建立了真空模块的力学模型，求解得到直角面越障过程中真空模块的最佳吸附力，并应用coppeliasim仿真求解出机器人关节驱动力矩，验证了李群李代数与旋量理论建模的正确性及动力学模型的有效性，通过吸附实验验证了真空模块吸附能力。
- 攀爬机器人 /
- 李群李代数 /
- 旋量理论 /
- 动力学建模
Abstract: Aiming at the problems of dynamic characteristics and vacuum module force balance in the process of climbing robot crossing obstacles, a climbing robot dynamics characteristic analysis method in the process of obstacle crossing motion is established based on the Lie group, Lie algebra and screw theory. The space velocity Jacobian matrix is deduced in the form of index product space thereby reducing the singularity generated due to the differential derivation, a clear physical meaning low computational complexity dynamic equation is established based on Lagrange equation, Lie group Lie algebra and screw theory. The mechanical model of the vacuum module is established, and the optimal adsorption force of the vacuum module is obtained during the obstacle crossing process. The driving torque of the robot joint is solved by coppeliasim simulation, which verified the correctness and dynamics of Lie group Lie algebra and screw theory modeling. The effectiveness of the scientific model is verified by the adsorption experiment to verify the optimal solution of the adsorption force.
- climbing robot /
- Lie group and Lie algebra /
- screw theory /
- dynamic modeling

HTML全文

图 1 攀爬机器人设计

下载: 全尺寸图片幻灯片

图 2 攀爬机器人运动步态

下载: 全尺寸图片幻灯片

图 3 攀爬机器人机构简图

下载: 全尺寸图片幻灯片

图 4 真空模块受力示意图

下载: 全尺寸图片幻灯片

图 5 攀爬机器人仿真模型

下载: 全尺寸图片幻灯片

图 6 攀爬机器人仿真速度曲线

下载: 全尺寸图片幻灯片

图 7 攀爬机器人仿真力矩曲线

下载: 全尺寸图片幻灯片

图 8 仿真与理论结果对比

下载: 全尺寸图片幻灯片

图 9 理论最佳吸附力

下载: 全尺寸图片幻灯片

图 10 吸附实验

下载: 全尺寸图片幻灯片

表 1 攀爬机器人结构参数

结构参数	数值
真空模块质量m₁/kg	5.01
转臂1质量m₂/kg	0.34
转臂2质量m₃/kg	1.98
关节O₂至腔底距离L₁/mm	230.24
转臂1长度L₀/mm	90
转臂2长度L₂/mm	180
关节O₄至腔底距离L₄/mm	230.24
真空腔惯性矩阵I₁/(kg·cm^-2)
转臂2惯性矩阵I₂/(kg·cm^-2)

下载: 导出CSV

表 2 吸附实验数据

材料	摩擦因数μ	关节O₂力矩τ₂/Nm	吸附力F_k/N
聚四氟乙烯	0.71	20.8, 19.7	141.5, 152.5
发泡硅胶	1.11	19.3, 21.1	149.9, 164.3
人造皮革	1.30	19.9, 21.6	152.8, 168.3

下载: 导出CSV

参考文献(27)

[1]	LI B, JIN J F, GU S Q, et al. The preliminary study of wall climbing firefighting rescue robot for high-rise and super high-rise building[J]. Applied Mechanics and Materials, 2013, 404: 569-574 doi: 10.4028/www.scientific.net/AMM.404.569
[2]	DANIEL G S. Autonomous staircase climbing robot for rescue application[J]. IOP Conference Series: Materials Science and Engineering, 2020, 912: 032085 doi: 10.1088/1757-899X/912/3/032085
[3]	CHU B, JUNG K, HAN C S, et al. A survey of climbing robots: Locomotion and adhesion[J]. International Journal of Precision Engineering and Manufacturing, 2010, 11(4): 633-647 doi: 10.1007/s12541-010-0075-3
[4]	TUMMALA R L, MUKHERJEE R, XI N, et al. Climbing the walls[robots][J]. IEEE Robotics and Automation Magazine, 2002, 9(4): 10-19 doi: 10.1109/MRA.2002.1160067
[5]	XIE D S, LIU J B, KANG R J, et al. Fully 3D-printed modular pipe-climbing robot[J]. IEEE Robotics and Automation Letters, 2021, 6(2): 462-469 doi: 10.1109/LRA.2020.3047795
[6]	GAO F M, FAN J C, ZHANG L B, et al. Magnetic crawler climbing detection robot basing on metal magnetic memory testing technology[J]. Robotics and Autonomous Systems, 2020, 125: 103439 doi: 10.1016/j.robot.2020.103439
[7]	JI A H, ZHAO Z H, MANOONPONG P, et al. A bio-inspired climbing robot with flexible pads and claws[J]. Journal of Bionic Engineering, 2018, 15(2): 368-378 doi: 10.1007/s42235-018-0028-6
[8]	DEGANI A. Dynamic single actuator robot climbing a chute[J]. Meccanica, 2016, 51(5): 1227-1243 doi: 10.1007/s11012-015-0286-x
[9]	王云倩, 牟玉壮, 张剑. 基于CPG控制的六足爬壁机器人自主越障研究[J]. 哈尔滨工程大学学报, 2018, 39(3): 584-593 https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201803027.htm WANG Y Q, MOU Y Z, ZHANG J. Autonomous obstacle crossing of a wall-climbing hexapod robot based on CPG control[J]. Journal of Harbin Engineering University, 2018, 39(3): 584-593 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201803027.htm
[10]	AUSTIN M P, HARPER M Y, BROWN J M, et al. Navigation for legged mobility: dynamic climbing[J]. IEEE Transactions on Robotics, 2020, 36(2): 537-544 doi: 10.1109/TRO.2019.2958207
[11]	XU F Y, SHEN J J, JIANG G P, et al. Kinematic and dynamic analysis of a cable-climbing robot[J]. International Journal of Advanced Robotic Systems, 2015, 12(7): 1-17
[12]	DU Q L, LU X P, WANG Y K, et al. The obstacle-surmounting analysis of a pole-climbing robot[J]. International Journal of Advanced Robotic Systems, 2020, 17(6): 1-20
[13]	秦基伟, 常勇, 袁兵兵, 等. 一种滚动密封式爬壁机器人动力学建模与分析[J]. 中国机械工程, 2019, 30(24): 2978-2985 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201924014.htm QIN J W, CHANG Y, YUAN B B, et al. Dynamics modeling and analysis of a rolling sealed wall-climbing robot[J]. China Mechanical Engineering, 2019, 30(24): 2978-2985 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201924014.htm
[14]	徐亚茹, 刘荣. 一种爬壁机器人动力学建模方法[J]. 北京航空航天大学学报, 2018, 44(2): 280-285 doi: 10.13700/j.bh.1001-5965.2017.0097 XU Y R, LIU R. An approach for dynamic modeling of climbing robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(2): 280-285 (in Chinese) doi: 10.13700/j.bh.1001-5965.2017.0097
[15]	NAM S M, OH J, LEE G, et al. Dynamic analysis during internal transition of a compliant multi-body climbing robot with magnetic adhesion[J]. Journal of Mechanical Science and Technology, 2014, 28(12): 5175-5187
[16]	董伟光, 王洪光, 姜勇. 一种轮足复合式爬壁机器人动力学建模与分析[J]. 机器人, 2015, 37(3): 264-270 https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR201503002.htm DONG W G, WANG H G, JIANG Y. Dynamics modeling and analysis of a wall-climbing robot with biped-wheel hybrid locomotion mechanism[J]. Robot, 2015, 37(3): 264-270 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR201503002.htm
[17]	LU Y, ZHOU K K, YE N J. Design and kinemics/ dynamics analysis of a novel climbing robot with tri-planar limbs for remanufacturing[J]. Journal of Mechanical Science and Technology, 2017, 31(3): 1427-1436
[18]	LEE K, WANG Y F, CHIRIKJIAN G S. O(n) mass matrix inversion for serial manipulators and polypeptide chains using Lie derivatives[J]. Robotica, 2007, 25(6): 739-750
[19]	CHEN G L, WANG H, LIN Z Q. Determination of the identifiable parameters in robot calibration based on the POE formula[J]. IEEE Transactions on Robotics, 2014, 30(5): 1066-1077
[20]	YANG K, YANG W Y, WANG C M. Inverse dynamic analysis and position error evaluation of the heavy-duty industrial robot with elastic joints: an efficient approach based on Lie group[J]. Nonlinear Dynamics, 2018, 93(2): 487-504
[21]	吕志忠, 张成维, 钟功祥, 等. 一种四足磁吸附爬壁机器人运动学分析及仿真[J]. 工程科学与技术, 2020, 52(2): 121-129 https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH202002015.htm LYU Z Z, ZHANG C W, ZHONG G X, et al. Kinematics analysis and simulation of a quadruped magnetic adsorption wall-climbing robot[J]. Advanced Engineering Sciences, 2020, 52(2): 121-129 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH202002015.htm
[22]	张高巍, 杨鹏, 王婕, 等. 可穿戴五自由度上肢外骨骼机器人固定时间控制[J]. 控制理论与应用, 2020, 37(1): 205-214 https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY202001023.htm ZHANG G W, YANG P, WANG J, et al. Fixed-time control for wearable 5 degrees of freedom upper-limb exoskeleton[J]. Control Theory and Applications, 2020, 37(1): 205-214 https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY202001023.htm
[23]	郭冰菁, 韩建海, 李向攀, 等. 步态康复机器人动力学李群李代数建模及仿真[J]. 系统仿真学报, 2020, 32(6): 1126-1135 https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202006016.htm GUO B J, HAN J H, LI X P, et al. Dynamics modeling and simulation of gait rehabilitation robot based on lie groups and lie algebras theory[J]. Journal of System Simulation, 2020, 32(6): 1126-1135 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ202006016.htm
[24]	韩博, 韩媛媛, 许允斗, 等. 基于螺旋理论的四面体可展机构运动特性与动力学分析[J]. 机器人, 2020, 42(1): 21-28 https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR202001003.htm HAN B, HAN Y Y, XU Y D, et al. Kinematic characteristics and dynamics analysis of the tetrahedral deployable mechanism based on the screw theory[J]. Robot, 2020, 42(1): 21-28 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JQRR202001003.htm
[25]	马广英, 刘润晨, 陈原, 等. 4足机器人腿部机构运动学分析及步态规划[J]. 北京理工大学学报, 2020, 40(4): 401-408 https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG202004008.htm MA G Y, LIU R C, CHEN Y, et al. Kinematics analysis and gait planning of the quadruped robot leg mechanism[J]. Transactions of Beijing Institute of Technology, 2020, 40(4): 401-408 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG202004008.htm
[26]	房海蓉, 李壮壮. 新型大转角2T2R并联机构的设计与分析[J]. 北京航空航天大学学报, 2020, 46(3): 465-473 https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK202003002.htm FANG H R, LI Z Z. Design and analysis of a new large rotation angle 2T2R parallel mechanism[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(3): 465-473 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK202003002.htm
[27]	戴建生. 机构学与机器人学的几何基础与旋量代数[M]. 北京: 高等教育出版社, 2014 DAI J S. Geometrical foundations and screw algebra for mechanisms and robotics[M]. Beijing: Higher Education Press, 2014 (in Chinese)