直线电机进给系统轮廓误差预测控制方法及仿真研究

杨泽青; 刘奇; 薄敬东; 刘丽冰; 魏强

doi:10.13433/j.cnki.1003-8728.20200567

直线电机进给系统轮廓误差预测控制方法及仿真研究

doi: 10.13433/j.cnki.1003-8728.20200567

杨泽青^{1, 2,},
刘奇^{1, 2},
薄敬东^{1, 3, ,},
刘丽冰^{1, 2},
魏强^{1, 2}

1.
河北工业大学机械工程学院，天津　300130
2.
国家技术创新方法与实施工具工程技术研究中心，天津　300401
3.
华北理工大学电气工程学院，河北唐山　063210

基金项目: 国家自然科学基金项目（52175461）、天津市智能制造专项（20201199）、河北省自然科学基金和重点基础研究专项项目（E2017202294）及天津市自然科学基金项目（16JCYBJC19100）

详细信息

作者简介:
杨泽青（1982−），副教授，博士，研究方向为高精度数控机床特性测试与控制，视觉缺陷检测与分类识别，yzq82@163.com

通讯作者:
薄敬东，讲师，博士研究生，bojingdong@163.com

中图分类号: TG502.1
计量
- 文章访问数: 27
- HTML全文浏览量: 7
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-05
- 刊出日期: 2023-03-25

Contour Error Predictive Control Methodology and Simulation of Linear Motor Feeding System

YANG Zeqing^{1, 2
,},
LIU Qi^{1, 2},
BO Jingdong^{1, 3
, ,},
LIU Libing^{1, 2},
WEI Qiang^{1, 2}

1.
School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China
2.
National Engineering Research Center for Technological Innovation Method and Tool, Tianjin 300401, China
3.
School of Electrical Engineering, North China University of Science and Technology,Tangshan 063210, Hebei, China

摘要

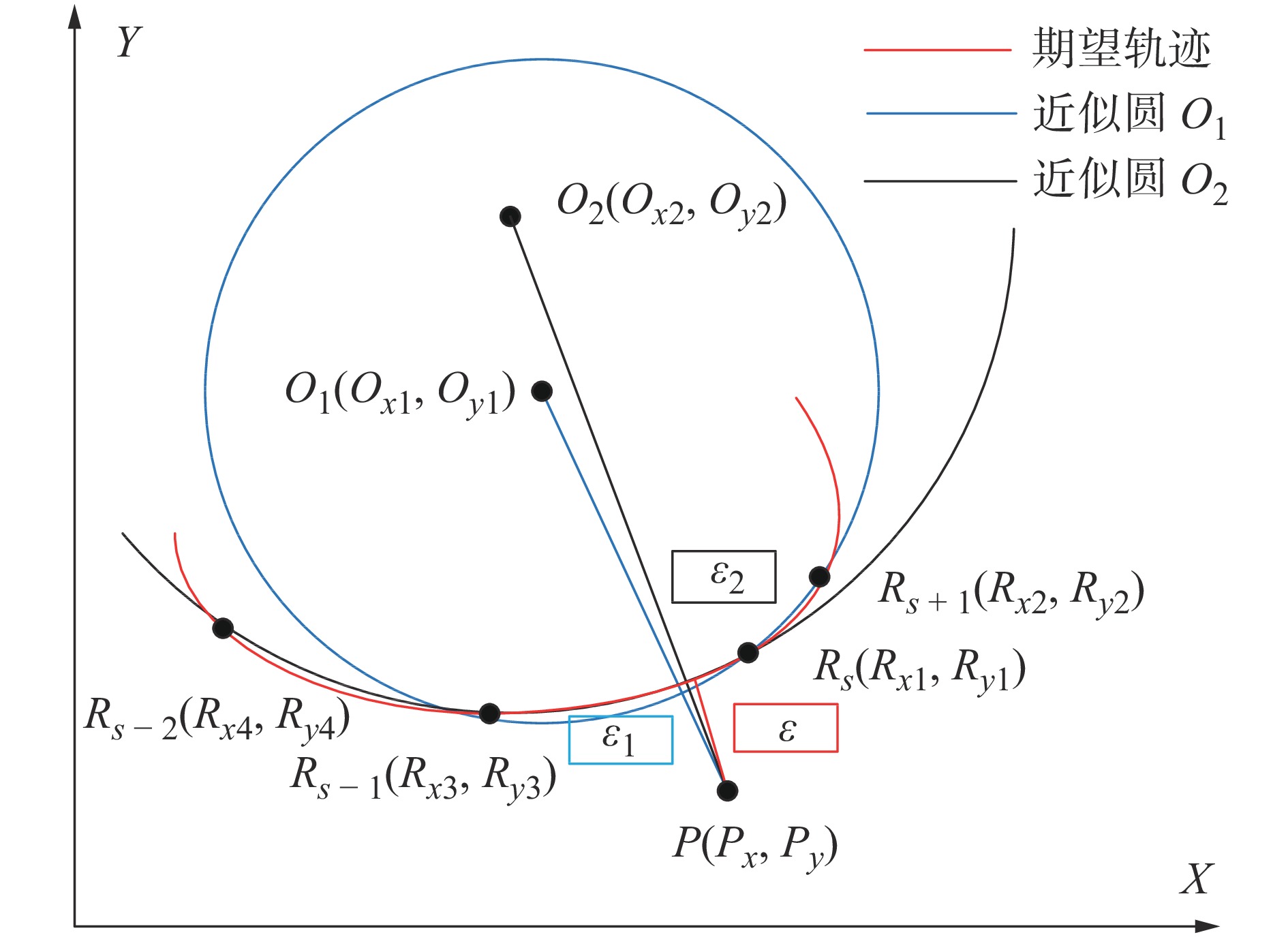
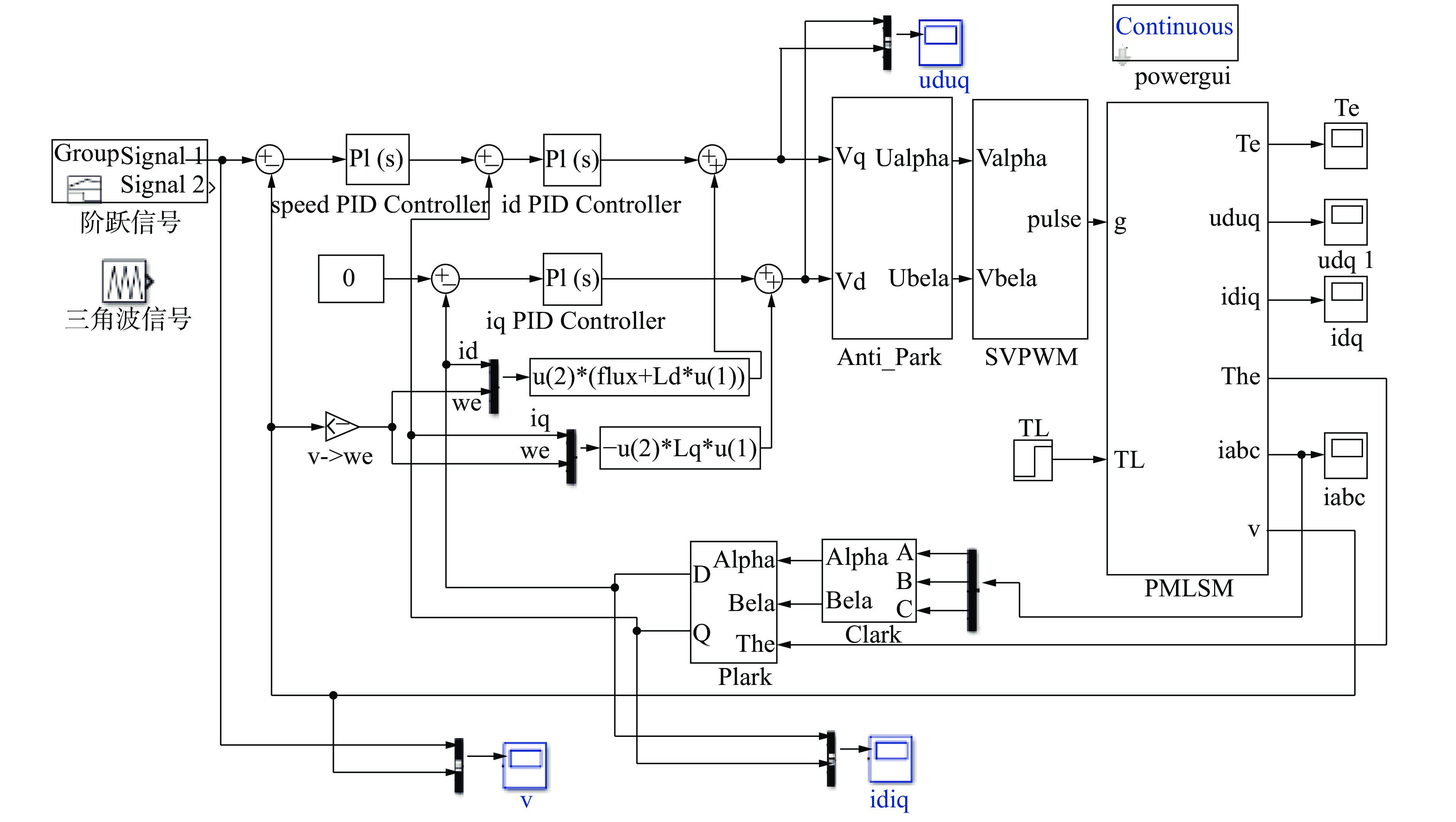
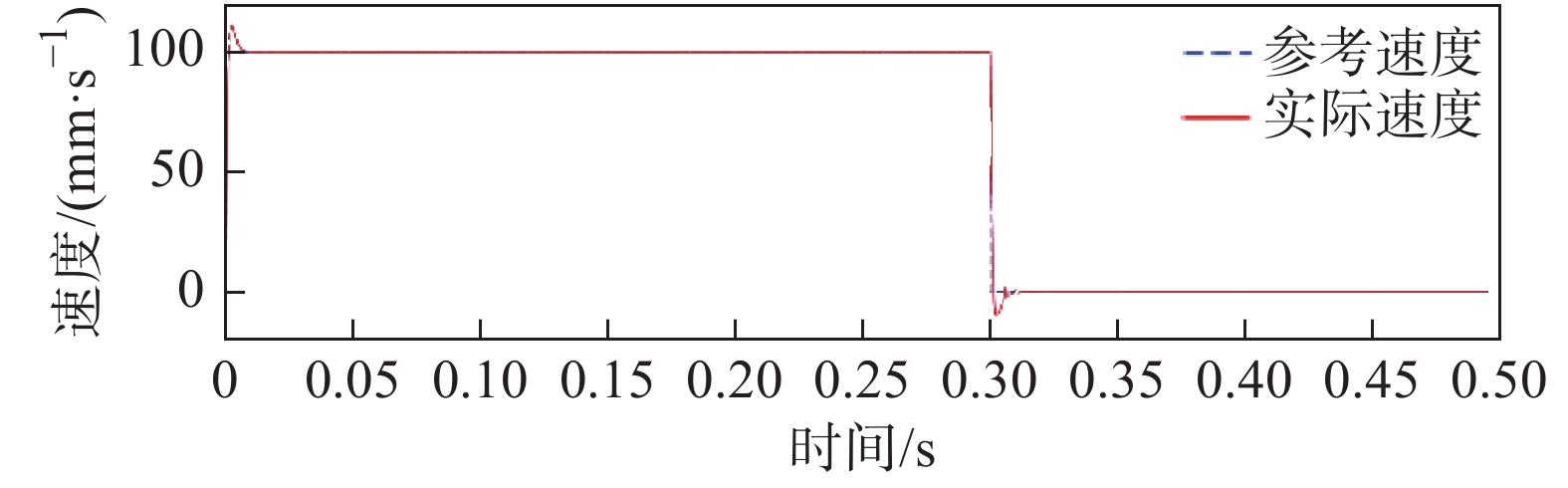
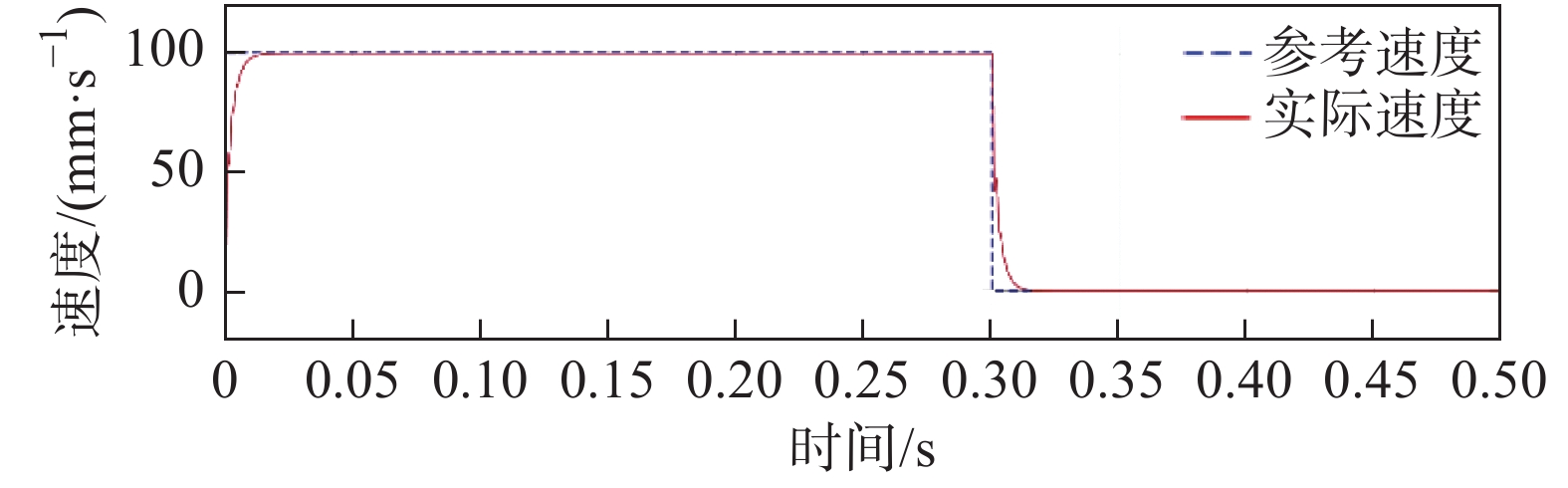
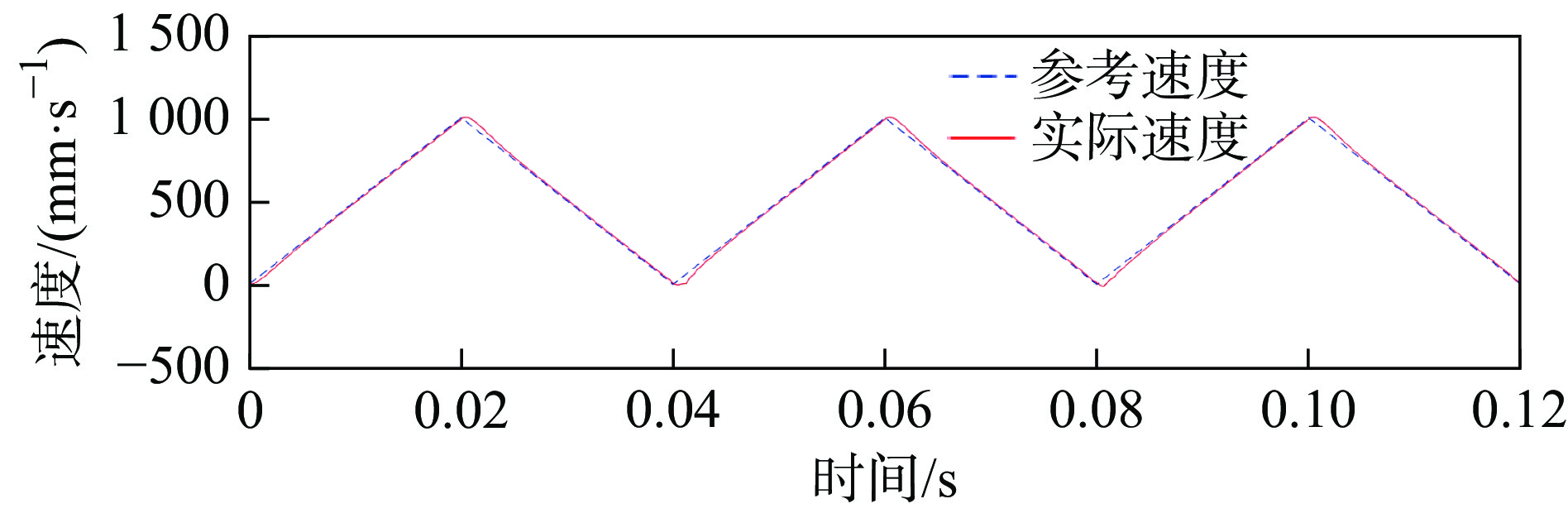
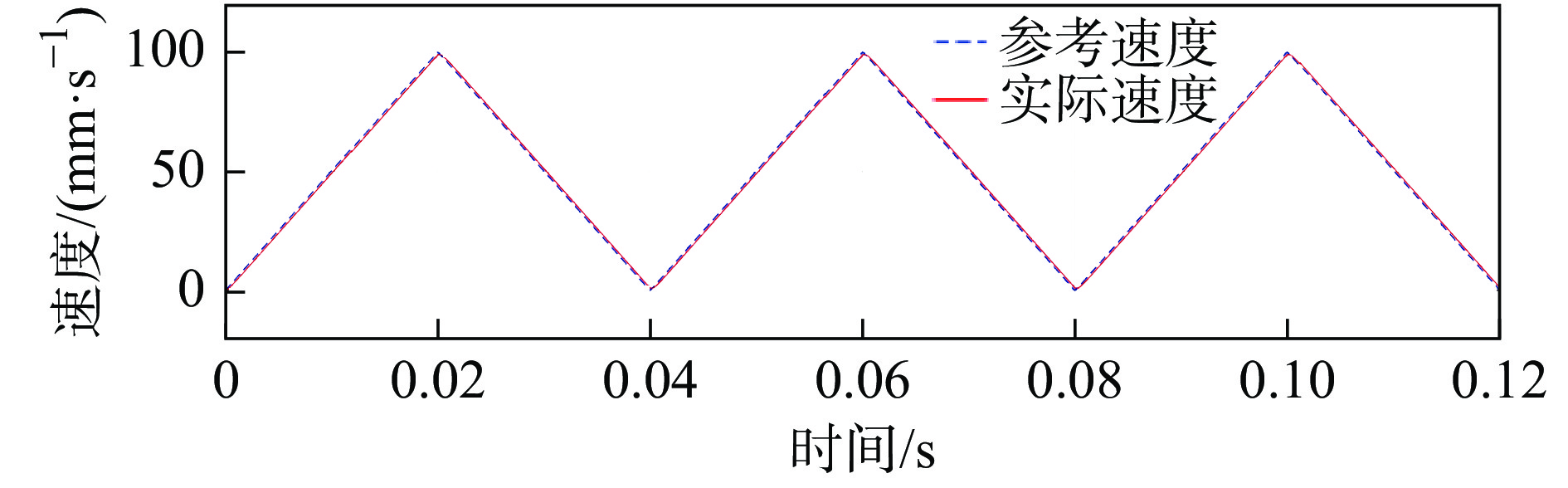
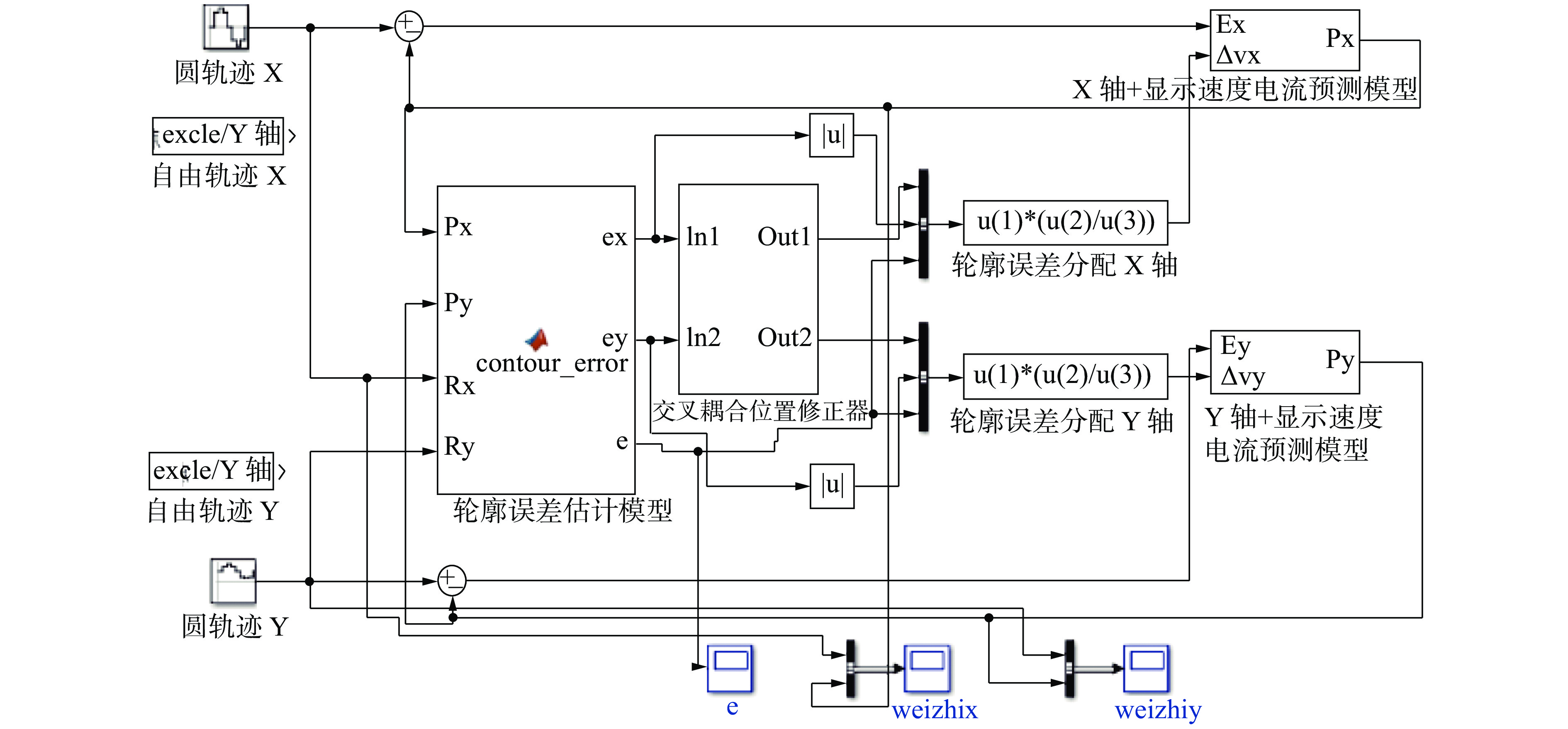
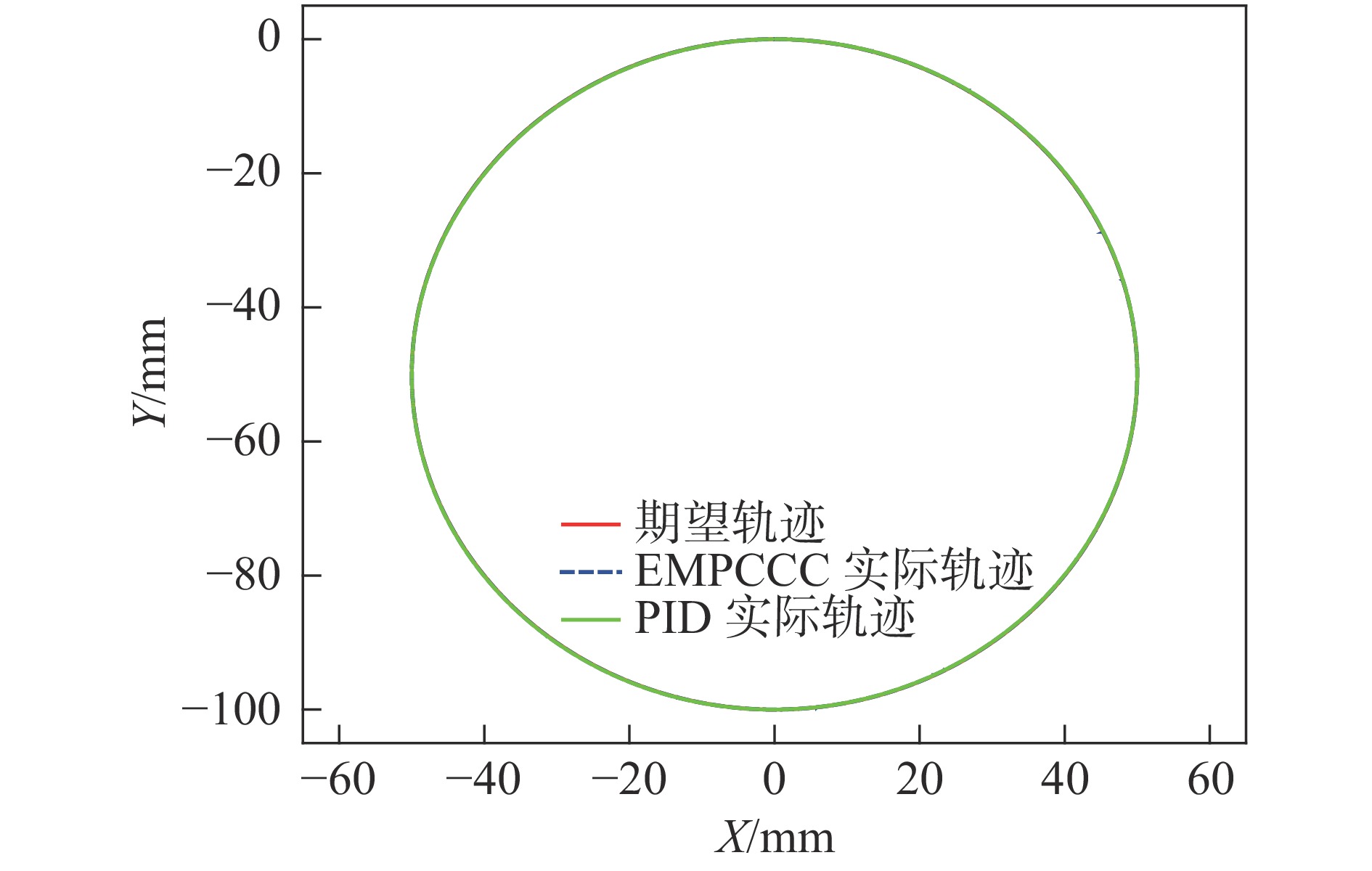
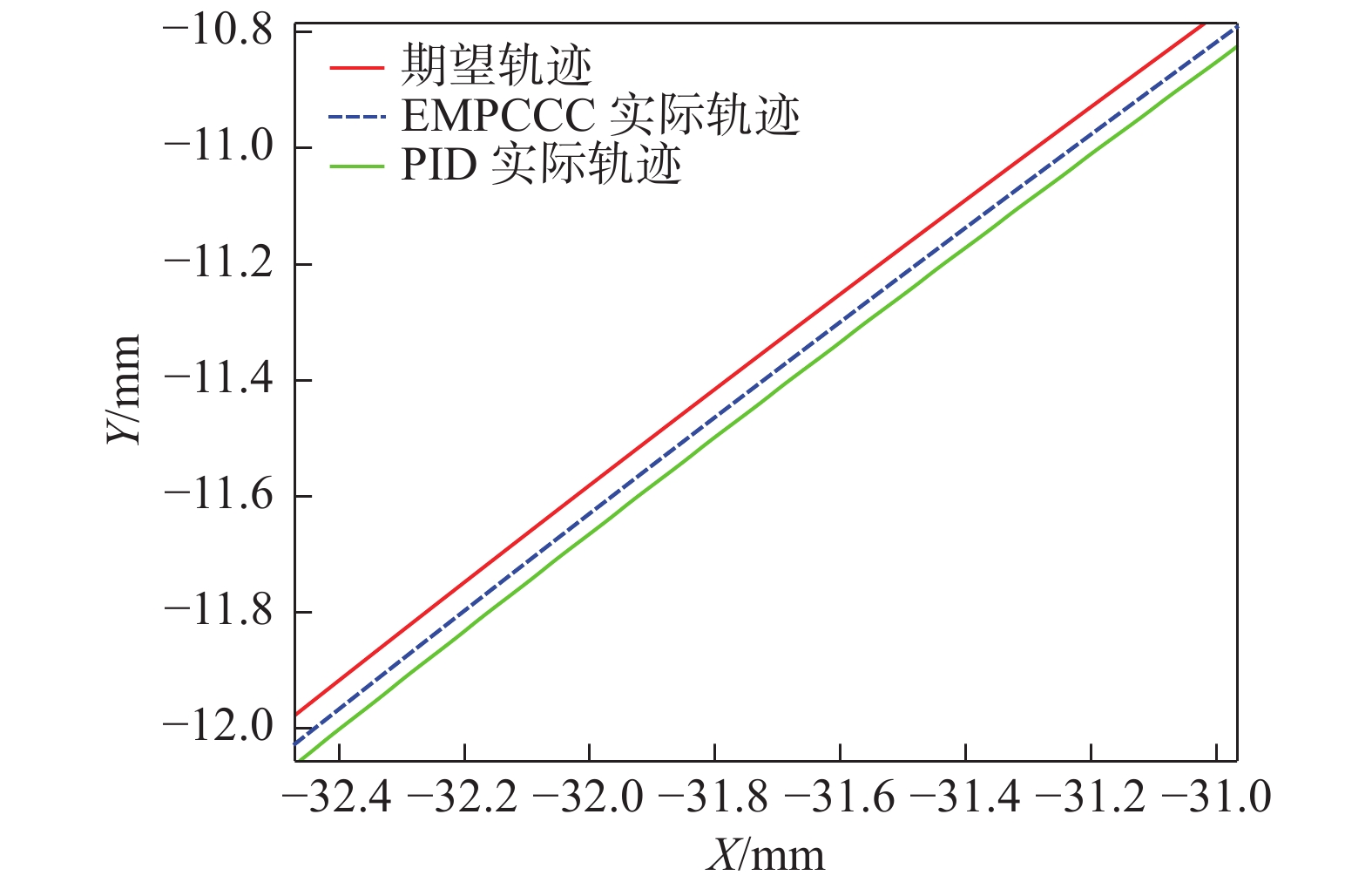
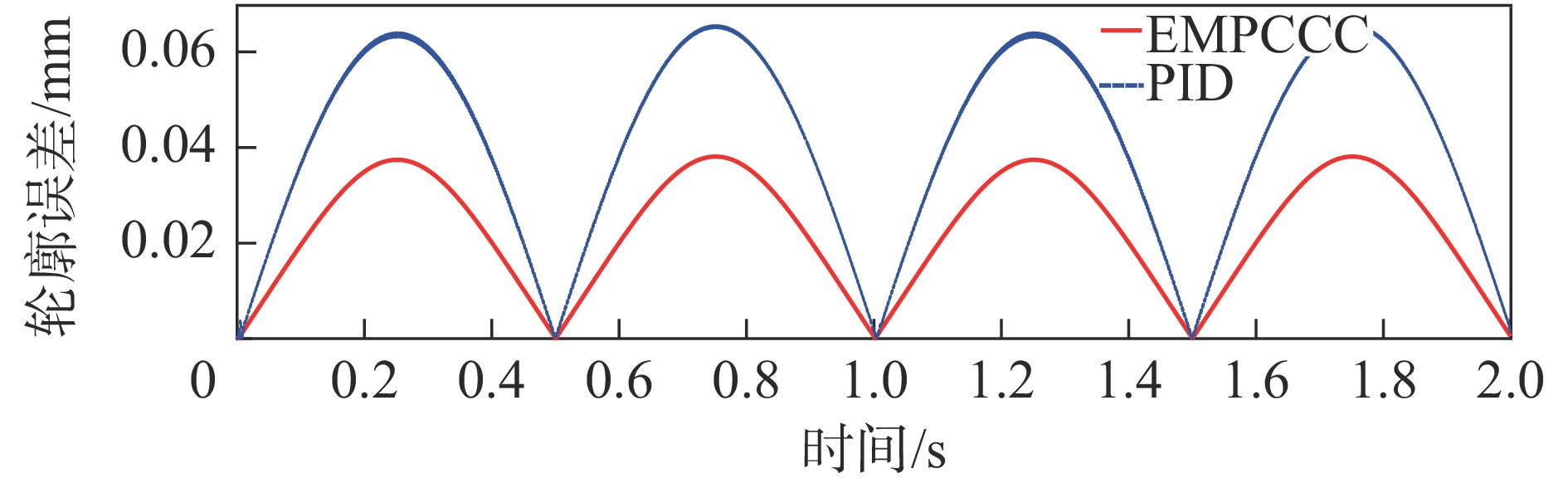
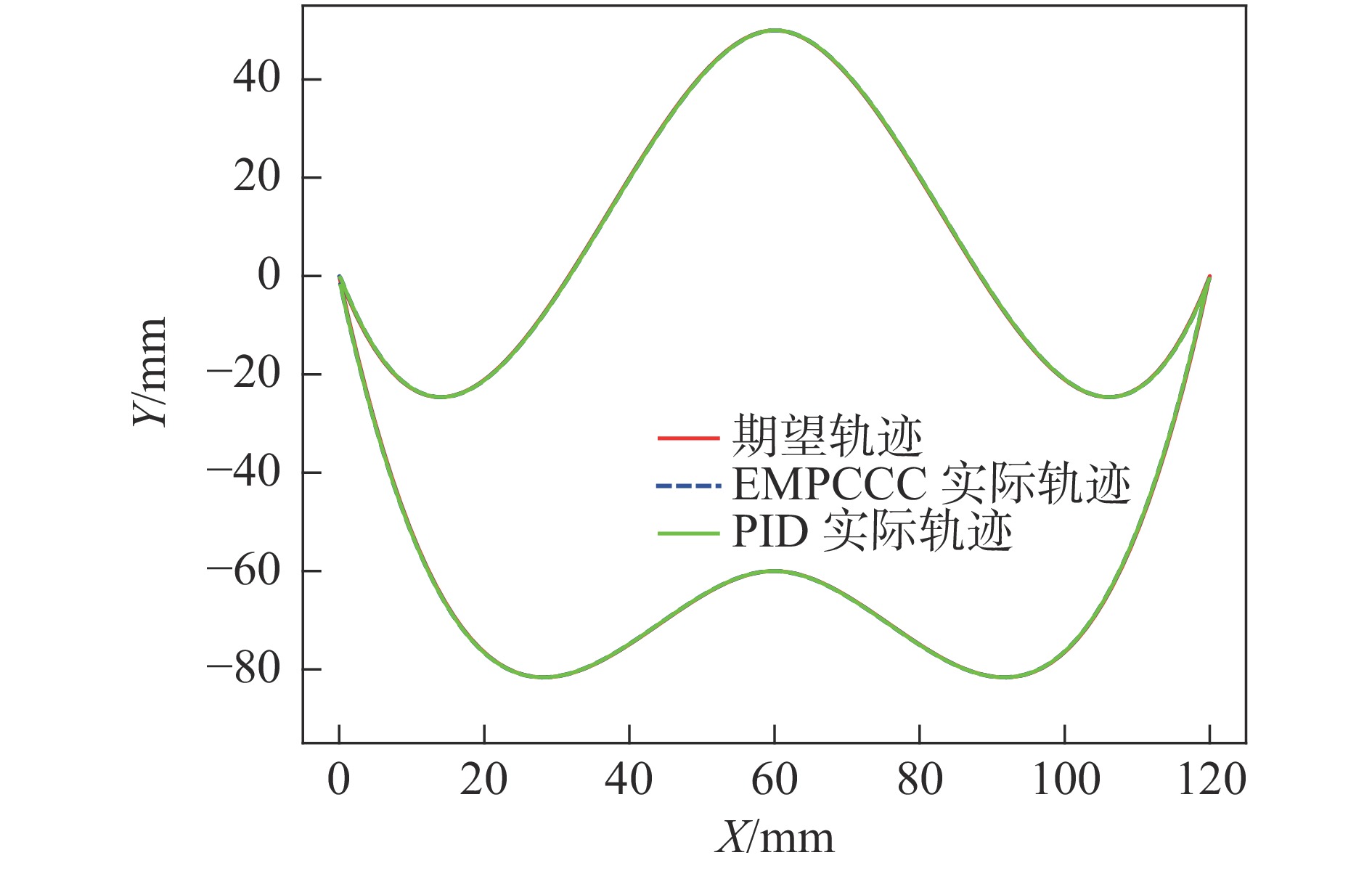
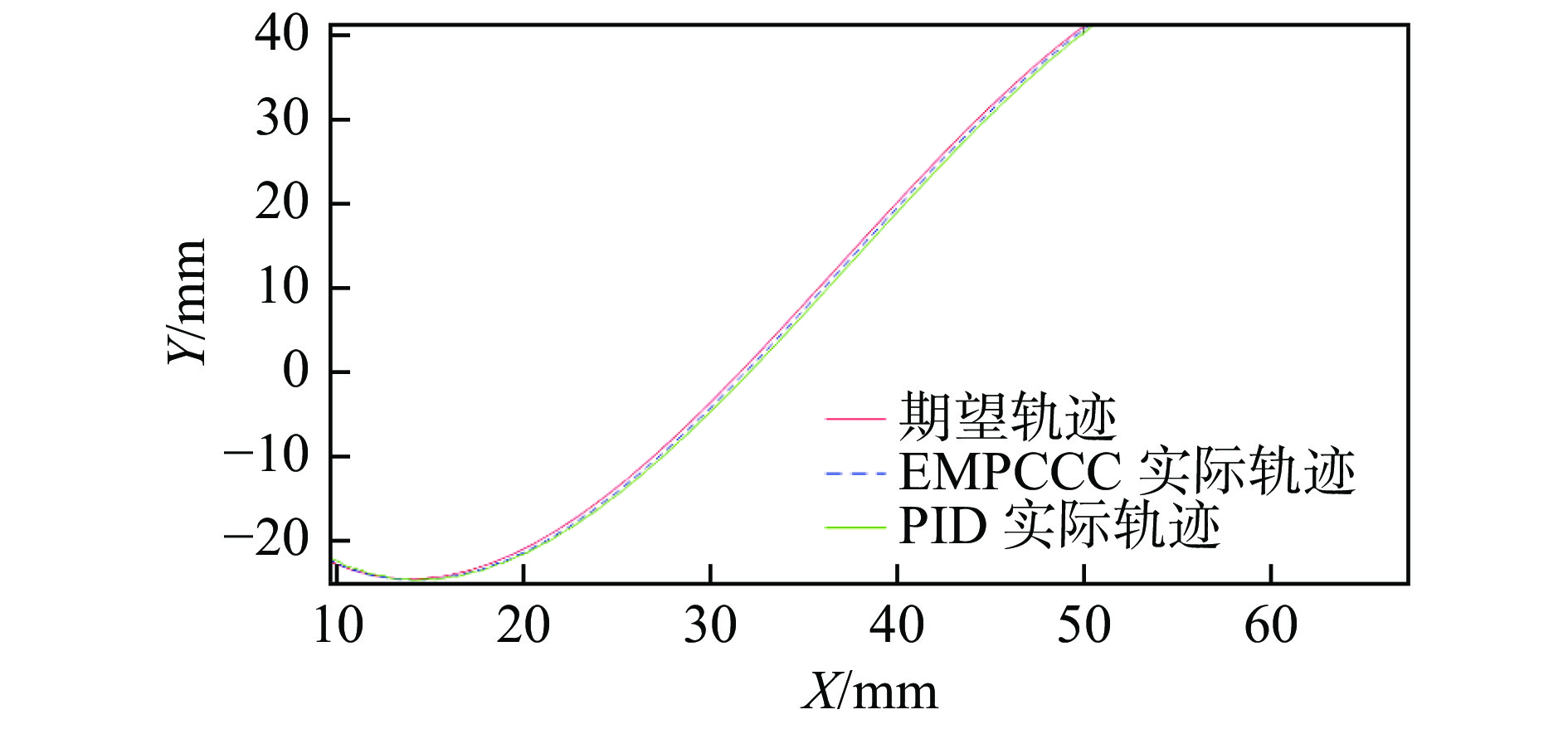
摘要: 为提高永磁同步直线电机驱动的进给系统轮廓轨迹跟踪精度和系统的动态性能，提出了一种显式模型预测交叉耦合控制方法（Explicit model predictive cross-coupled control, EMPCCC）。该方法结合显式预测控制原理与交叉耦合控制思想，对单轴电流和速度信号进行多步预测，将轮廓误差作为反馈量来修正预测控制的给定轨迹，达到轮廓误差预测控制的目的。基于MATLAB/Simulink搭建仿真模型，结果表明，所提EMPCCC方法能快速实现不同转速波形的无超调跟踪控制，且可以实时估计并补偿轮廓误差，提升不同轨迹的轮廓精度。
- 永磁同步直线电机 /
- 轮廓误差 /
- 模型预测控制 /
- 交叉耦合控制
Abstract: An explicit model predictive cross-coupled control (EMPCCC) method is proposed to improve the contour trajectory tracking accuracy and the dynamic performance of the system driven by a permanent magnet synchronous linear motor.The method combines the explicit predictive control with cross-coupling control to perform multi-step prediction of single-axis current and velocity signals, and use the contour error as a feedback quantity to correct the given trajectory of the predictive control to achieve the purpose of contour error predictive control.Finally, the simulation model is built based on MATLAB/Simulink, and the simulation results show that the EMPCCC method can quickly achieve overshoot-free tracking control of different speed waveforms, and it can estimate and compensate the contour error to improve the contour accuracy of different trajectories.
- permanent magnet synchronous linear motors /
- contour errors /
- model predictive control /
- cross-coupling control

HTML全文

图 1 典型轨迹轮廓误差模型示意图

下载: 全尺寸图片幻灯片

图 2 多点圆近似法自由曲线轮廓误差估计模型

下载: 全尺寸图片幻灯片

图 3 显式模型预测交叉耦合控制系统框图

下载: 全尺寸图片幻灯片

图 4 显式速度-电流预测模型图

下载: 全尺寸图片幻灯片

图 5 单轴PID级联控制仿真模型图

下载: 全尺寸图片幻灯片

图 6 单轴显式速度-电流预测控制仿真模型图

下载: 全尺寸图片幻灯片

图 7 单轴PID级联控制方法阶跃响应

下载: 全尺寸图片幻灯片

图 8 单轴显式速度-电流预测控制方法阶跃响应

下载: 全尺寸图片幻灯片

图 9 单轴PID级联控制方法三角波信号响应

下载: 全尺寸图片幻灯片

图 10 单轴显式速度-电流预测控制方法三角波信号响应

下载: 全尺寸图片幻灯片

图 11 EMPCCC控制仿真模型图

下载: 全尺寸图片幻灯片

图 12 圆轨迹EMPCCC方法与PID方法对比图

下载: 全尺寸图片幻灯片

图 13 圆轨迹放大对比图

下载: 全尺寸图片幻灯片

图 14 圆轨迹轮廓误差图

下载: 全尺寸图片幻灯片

图 15 自由轨迹EMPCCC方法与PID方法对比图

下载: 全尺寸图片幻灯片

图 16 自由轨迹放大对比图

下载: 全尺寸图片幻灯片

图 17 自由轨迹轮廓误差图

下载: 全尺寸图片幻灯片

表 1 永磁同步直线电机参数

电机参数	数值
相电阻R_s/Ω	4.7
交轴、直轴电感L_d、L_q / mH	34
电机粘性阻尼系数B/（N·s·m⁻¹）	0.035 14
永磁体磁链ψ_f / Wb	0.308 79
转动惯量J /10⁻⁴ (kg·m²)	2.64
负载转矩T_L/10⁻² (N·m)	4.536 7

下载: 导出CSV

参考文献(23)

[1]	杨晓君, 赵万华, 刘辉, 等. 直线电机进给系统机械系统动态特性研究[J]. 西安交通大学学报, 2013, 47(4): 44-50. YANG X J, ZHAO W H, LIU H, et al. Dynamic characteristics of mechanical system in linear motor feed system[J]. Journal of Xi'an Jiaotong University, 2013, 47(4): 44-50. (in Chinese)
[2]	LIU C, WU J H, LIU J, et al. High acceleration motion control based on a time-domain identification method and the disturbance observer[J]. Mechatronics, 2014, 24(6): 672-678. doi: 10.1016/j.mechatronics.2014.01.001
[3]	BOLDER J, OOMEN T. Rational basis functions in iterative learning control-with experimental verification on a motion system[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 722-729. doi: 10.1109/TCST.2014.2327578
[4]	徐鸣飞, 胡敏强, 余海涛, 等. 基于复合模糊控制和ZPETC的无铁心直线电机控制器的仿真研究[J]. 微电机, 2015, 48(7): 38-42. XU M F, HU M Q, YU H T, et al. Simulation research of coreless linear motor controller based on composite fuzzy control and ZPETC[J]. Micromotors, 2015, 48(7): 38-42. (in Chinese)
[5]	杨红, 李生明. 高精度定位系统的摩擦力自适应前馈补偿[J]. 电气传动, 2021, 51(4): 22-26. YANG H, LI S M. Friction adaptive feedforward compensation for high precision positioning system[J]. Electric Drive, 2021, 51(4): 22-26. (in Chinese)
[6]	KOREN Y. Cross-coupled biaxial computer control for manufacturing systems[J]. Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4): 265-272. doi: 10.1115/1.3149612
[7]	KOREN Y, LO C C. Variable-gain cross-coupling controller for contouring[J]. CIRP Annals, 1991, 40(1): 371-374. doi: 10.1016/S0007-8506(07)62009-5
[8]	SHIH Y T, CHEN C S, LEE A C. A novel cross-coupling control design for Bi-axis motion[J]. International Journal of Machine Tools and Manufacture, 2002, 42(14): 1539-1548. doi: 10.1016/S0890-6955(02)00109-8
[9]	YEH S S, HSU P L. Estimation of the contouring error vector for the cross-coupled control design[J]. IEEE/ASME Transactions on Mechatronics, 2002, 7(1): 44-51. doi: 10.1109/3516.990886
[10]	李培新, 马跃, 于东, 等. 一种实时轮廓误差估算方法[J]. 中国机械工程, 2011, 22(4): 419-423. LI P X, MA Y, YU D, et al. A method of real-time estimation of contouring errors[J]. China Mechanical Engineering, 2011, 22(4): 419-423. (in Chinese)
[11]	CHIU G T C, TOMIZUKA M. Contouring control of machine tool feed drive systems: a task coordinate frame approach[J]. IEEE Transactions on Control Systems Technology, 2001, 9(1): 130-139. doi: 10.1109/87.896754
[12]	YAO B, HU C X, WANG Q F. An orthogonal global task coordinate frame for contouring control of biaxial systems[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(4): 622-634. doi: 10.1109/TMECH.2011.2111377
[13]	李祥飞, 赵欢, 赵鑫, 等. 面向伺服动态特性匹配的轮廓误差补偿控制研究[J]. 机械工程学报, 2017, 53(1): 150-156. LI X F, ZHAO H, ZHAO X, et al. Research on contour error compensation method with matched servo dynamic characteristics[J]. Journal of Mechanical Engineering, 2017, 53(1): 150-156. (in Chinese)
[14]	EL KHALICK M A, UCHIYAMA N. Estimation of tool orientation contour errors for five-axismachining[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(5): 271-277. doi: 10.1016/j.rcim.2013.01.002
[15]	喻曦, 赵欢, 李祥飞, 等. 基于双深度神经网络的轮廓误差补偿策略研究[J]. 机械工程学报, 2019, 55(3): 130-137. doi: 10.3901/JME.2019.03.130 YU X, ZHAO H, LI X F, et al. Research on contouring error compensation method using dual deep neural networks[J]. Journal of Mechanical Engineering, 2019, 55(3): 130-137. (in Chinese) doi: 10.3901/JME.2019.03.130
[16]	汪昕杨, 刘亚超, 钟永彬, 等. 基于自校正自抗扰控制的多电机协同系统[J]. 组合机床与自动化加工技术, 2021(2): 77-81. WANG X Y, LIU Y C, ZHONG Y B, et al. Multi-motor coordinated system based on self-correction active disturbance rejection control[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(2): 77-81. (in Chinese)
[17]	金昊, 丁曙光. 基于GA优化RBF网络的永磁同步电机无位置控制[J]. 组合机床与自动化加工技术, 2021(2): 95-98. JIN H, DING S G. Sensorless control of permanent magnet synchronous motor based on RBF neural network with genetic algorithm optimization[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(2): 95-98. (in Chinese)
[18]	HUO F, XI X C, POO A N. Generalized Taylor series expansion for free-form two-dimensional contour error compensation[J]. International Journal of Machine Tools and Manufacture, 2012, 53(1): 91-99. doi: 10.1016/j.ijmachtools.2011.10.001
[19]	MCNAB R J, TSAO T C. Receding time horizon linear quadratic optimal control for multi-axis contour tracking motion control[J]. Journal of Dynamic Systems, Measurement, and Control, 2000, 122(2): 375-381. doi: 10.1115/1.482476
[20]	MOGHADAM H Z, LANDERS R G, BALAKRISHNAN S N. Hierarchical optimal contour control of motion systems[J]. Mechatronics, 2014, 24(2): 98-107. doi: 10.1016/j.mechatronics.2013.12.007
[21]	刘旭东, 李珂, 张奇, 等. 基于非线性扰动观测器的永磁同步电机单环预测控制[J]. 中国电机工程学报, 2018, 38(7): 2153-2162. LIU X D, LI K, ZHANG Q, et al. Single-loop predictive control of PMSM based on nonlinear disturbance observers[J]. Proceedings of the CSEE, 2018, 38(7): 2153-2162. (in Chinese)
[22]	贾成禹, 王旭东, 周凯. 基于扰动观测器的PMSM模型预测电流控制[J]. 电力电子技术, 2019, 53(10): 23-25 + 95. JIA C Y, WANG X D, ZHOU K. Model predictive current control of PMSM based on disturbance observer[J]. Power Electronics, 2019, 53(10): 23-25 + 95. (in Chinese)
[23]	王岩强. 永磁同步电机模型预测控制技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 WANG Y Q. Research on model predictive control technology of PMSM[D]. Harbin: Harbin Institute of Technology, 2017. (in Chinese)