Fault Diagnosis Method of Rolling Bearing Combining with SPA Dispersion Entropy and GK Clustering
-
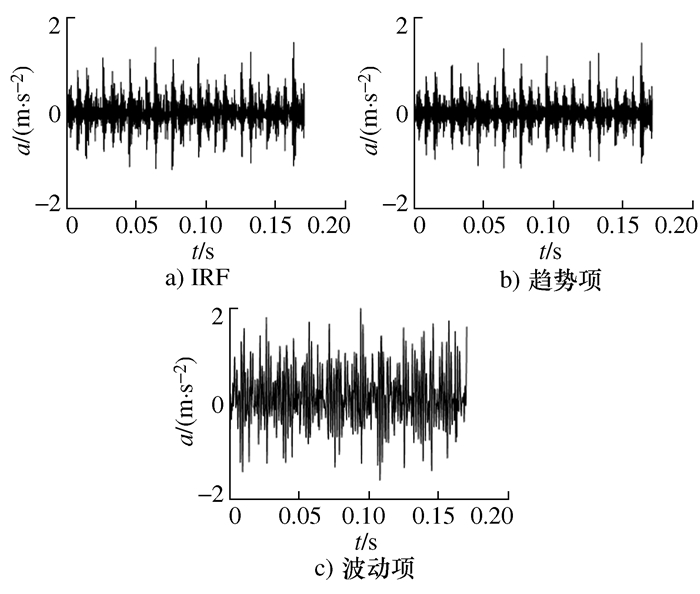
摘要: 为充分利用振动信号的特征信息进行故障辨识, 提出一种平滑先验分析(SPA)散布熵和GK聚类相结合的滚动轴承故障诊断方法。首先对滚动轴承振动信号进行SPA分解得到趋势项和波动项; 然后分别计算趋势项和波动项的散布熵值构建特征向量; 最后将特征向量输入至GK分类器中进行聚类识别。将该方法应用到不同工况下的滚动轴承实验数据中, 分析结果表明, 与传统的基于经验模态分解(EMD)散布熵和GK聚类的故障诊断方法相比, 所提方法能够更加准确地实现轴承的故障判别。Abstract: In order to make full use of the characteristic information of vibration signal for fault identification, a rolling bearing fault diagnosis method combining with smoothness priors approach (SPA) dispersion entropy and Gustafson-Kessel (GK) clustering was proposed in this paper. Firstly, the SPA algorithm was used to decompose the vibration signal of rolling bearings, and the trend and de-trend terms was obtained. Secondly, the dispersion entropy of the trend and de-trend was calculated to construct feature vectors. Finally, the feature vectors were input into the GK classifier for clustering and recognized. The proposed method was applied to the experimental data of rolling bearing in different working conditions. The results show that compared with the traditional fault diagnosis methods based on empirical mode decomposition (EMD) dispersion entropy and GK clustering, the proposed method can accurately achieve fault diagnosis of rolling bearings.
-
Key words:
- rolling bearing /
- smoothness priors approach /
- dispersion entropy /
- GK clustering /
- fault diagnosis
-
表 1 不同λ下趋势项及波动项与原信号的相关系数
λ 3 4 5 6 7 趋势项 0.969 0.973 0.976 0.979 0.981 波动项 0.375 0.333 0.309 0.294 0.283 表 2 不同状态信号的趋势项和波动项的散布熵值
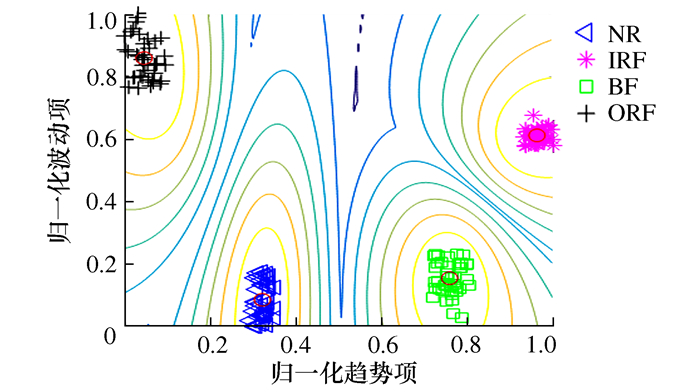
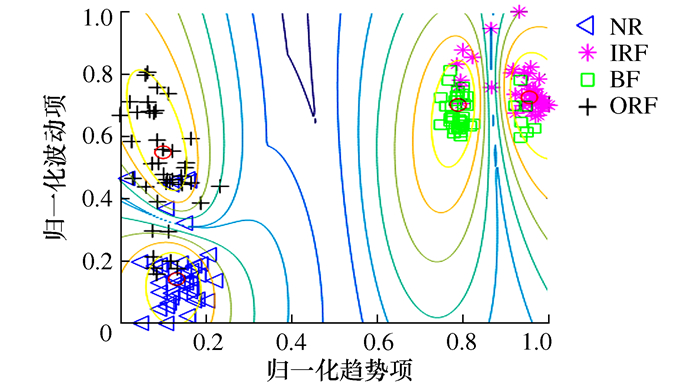
信号类型 趋势项 波动项 NR 4.16 3.40 IRF 4.85 3.60 ORF 3.87 3.70 BF 4.63 3.43 表 3 不同故障类型的聚类评价指标
诊断方法 PC CE SPA-DE-GK 0.978 1 0.066 6 EMD-DE-GK 0.873 4 0.246 9 表 4 不同损伤程度的聚类评价指标
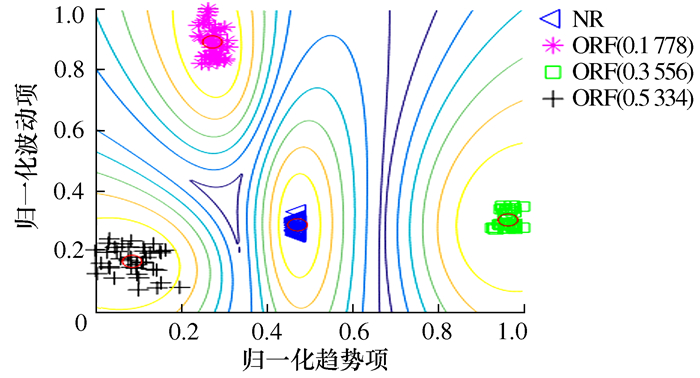
诊断方法 PC CE SPA-DE-GK 0.989 7 0.023 4 EMD-DE-GK 0.853 3 0.282 4 -
[1] 张龙, 吴荣真, 雷兵, 等. 基于多尺度熵的滚动轴承故障可拓智能识别[J]. 噪声与振动控制, 2019, 39(6): 200-205 doi: 10.3969/j.issn.1006-1355.2019.06.035ZHANG L, WU R Z, LEI B, et al. Extensible intelligent identification for rolling bearing faults using multiscale entropy[J]. Noise and Vibration Control, 2019, 39(6): 200-205 (in Chinese) doi: 10.3969/j.issn.1006-1355.2019.06.035 [2] 凌鹏, 陈跃威. 基于CEEMD互近似熵和FCM滚动轴承故障诊断[J]. 计算机仿真, 2018, 35(3): 314-318, 410 doi: 10.3969/j.issn.1006-9348.2018.03.068LING P, CHEN Y W. Fault diagnosis of rolling bearing based on CEEMD cross approximate entropy and fuzzy C means clustering[J]. Computer Simulation, 2018, 35(3): 314-318, 410 (in Chinese) doi: 10.3969/j.issn.1006-9348.2018.03.068 [3] 郑近德, 李从志, 潘海洋. 复合多尺度散布熵在滚动轴承故障诊断中的应用[J]. 噪声与振动控制, 2018, 38(S1): 653-656 https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK2018S2064.htmZHENG J D, LI C Z, PAN H Y. Application of composite multi-scale dispersion entropy in rolling bearing fault diagnosis[J]. Noise and Vibration Control, 2018, 38(S1): 653-656 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK2018S2064.htm [4] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 174102 doi: 10.1103/PhysRevLett.88.174102 [5] HAN M H, PAN J L. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings[J]. Measurement, 2015, 76: 7-19 doi: 10.1016/j.measurement.2015.08.019 [6] RICHMAN J S, MOORMAN J R. Physiological time- series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049 doi: 10.1152/ajpheart.2000.278.6.H2039 [7] ROSTAGHI M, AZAMI H. Dispersion entropy: a measure for time-series analysis[J]. IEEE Signal Processing Letters, 2016, 23(5): 610-614 doi: 10.1109/LSP.2016.2542881 [8] 李从志, 郑近德, 潘海洋, 等. 基于自适应多尺度散布熵的滚动轴承故障诊断方法[J]. 噪声与振动控制, 2018, 38(5): 173-179 doi: 10.3969/j.issn.1006-1355.2018.05.031LI C Z, ZHENG J D, PAN H Y, et al. Fault diagnosis method of rolling bearings based on adaptive multi-scale dispersion entropy[J]. Noise and Vibration Control, 2018, 38(5): 173-179 (in Chinese) doi: 10.3969/j.issn.1006-1355.2018.05.031 [9] YAN R Q, GAO R X, CHEN X F. Wavelets for fault diagnosis of rotary machines: a review with applications[J]. Signal Processing, 2014, 96: 1-15 doi: 10.1016/j.sigpro.2013.04.015 [10] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995 doi: 10.1098/rspa.1998.0193 [11] SMITH J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454 doi: 10.1098/rsif.2005.0058 [12] 丁闯, 张兵志, 冯辅周, 等. 局部均值分解和排列熵在行星齿轮箱故障诊断中的应用[J]. 振动与冲击, 2017, 36(17): 55-60 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201717009.htmDIND C, ZHANG B Z, FENG F Z, et al. Application of local mean decomposition and permutation entropy in fault diagnosis of planetary gearboxes[J]. Journal of Vibration and Shock, 2017, 36(17): 55-60 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201717009.htm [13] 李郁, 田卫军, 张前图. 基于变分模态分解互近似熵和相关向量机的轴承故障诊断[J]. 机械设计与研究, 2017, 33(6): 90-93, 97 https://www.cnki.com.cn/Article/CJFDTOTAL-JSYY201706026.htmLI Y, TIAN W J, ZHANG Q T. Bearing fault diagnosis based on variational mode decomposition cross approximate entropy and relevance vector machine[J]. Machine Design & Research, 2017, 33(6): 90-93, 97 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSYY201706026.htm [14] 赵荣珍, 李霁蒲, 邓林峰. EWT多尺度排列熵与GG聚类的轴承故障辨识方法[J]. 振动、测试与诊断, 2019, 39(2): 416-423, 451 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201902029.htmZHAO R Z, LI J P, DENG L F. Method integrate EWT multi-scale permutation entropy with GG clustering for bearing fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2019, 39(2): 416-423, 451 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201902029.htm [15] 戴邵武, 陈强强, 戴洪德, 等. 基于平滑先验分析和模糊熵的滚动轴承故障诊断[J]. 航空动力学报, 2019, 34(10): 2218-2226 https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI201910015.htmDAI S W, CHEN Q Q, DAI H D, et al. Rolling bearing fault diagnosis based on smoothness priors approach and fuzzy entropy[J]. Journal of Aerospace Power, 2019, 34(10): 2218-2226 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI201910015.htm [16] 黄海峰, 易武, 易庆林, 等. 滑坡位移分解预测中的平滑先验分析方法[J]. 水文地质工程地质, 2014, 41(5): 95-100 https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201405018.htmHUANG H F, YI W, YI Q L, et al. Smoothness priors approach in displacement decomposition and prediction of landslides[J]. Hydrogeology & Engineering Geology, 2014, 41(5): 95-100 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201405018.htm [17] 陈东宁, 张运东, 姚成玉, 等. 基于FVMD多尺度排列熵和GK模糊聚类的故障诊断[J]. 机械工程学报, 2018, 54(14): 16-27 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201814003.htmCHEN D N, ZHANG Y D, YAO C Y, et al. Fault diagnosis based on FVMD multi-scale permutation entropy and GK fuzzy clustering[J]. Journal of Mechanical Engineering, 2018, 54(14): 16-27 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201814003.htm -








 下载:
下载: