Application of Improved Cubic Spline Interpolation in Trajectory Planning of Manipulator
-
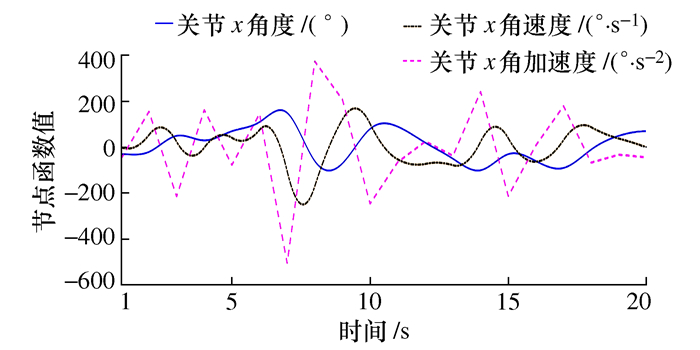
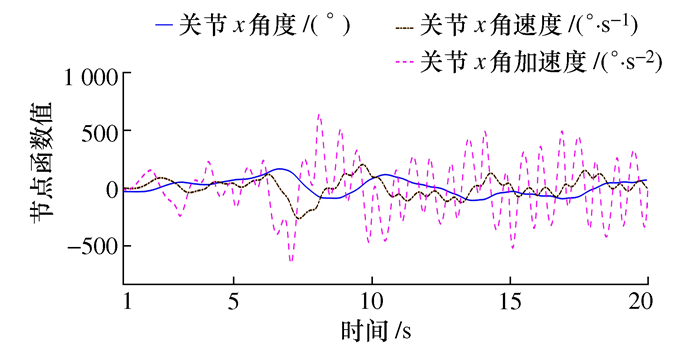
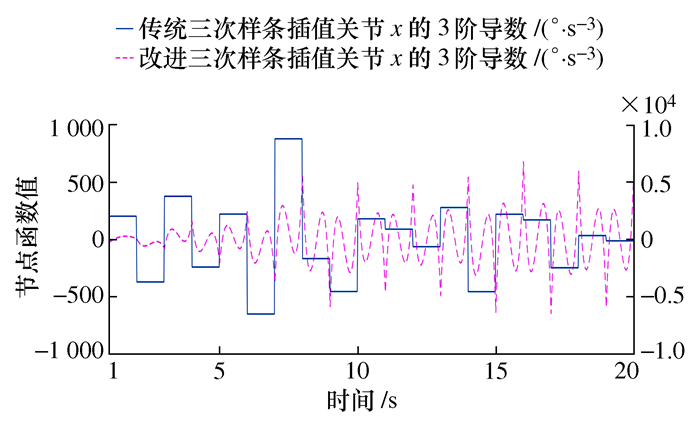
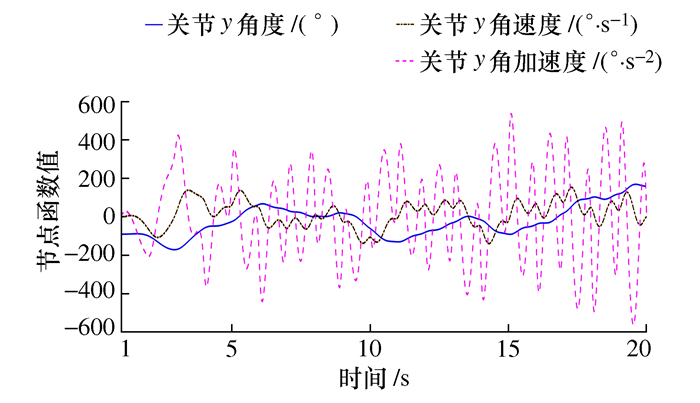
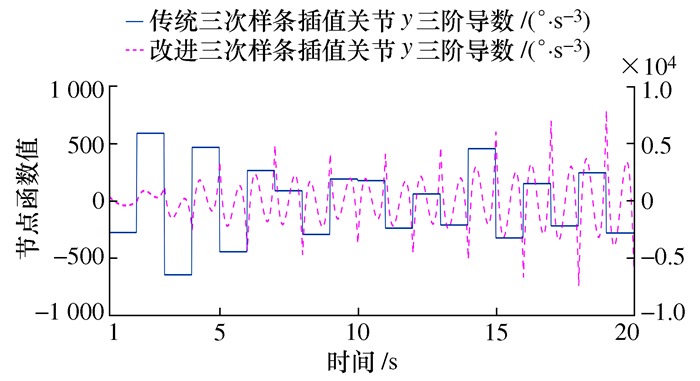
摘要: 针对传统三次样条插值在机械臂轨迹规划过程中关节轴易产生残余振动的问题,提出了一种三阶导数连续的改进三次样条轨迹规划方法。该方法在每一个三次样条插值的分段区间内都加入了一个修正因子,在第一个分段区间内的修正因子是五次修正函数,使关节轴起始加速度为零,其余分段区间均为六次修正函数,使关节轴运动轨迹的三阶导数连续和终止位置的加速度为零。本文对六关节轴机械臂选取了20个节点进行轨迹规划仿真,结果表明改进的样条插值方法在机械臂轨迹规划中得到了连续的三阶导数轨迹,有效减小了关节轴的残余振动。Abstract: Aiming at the problem that the joint axis is prone to residual vibration during the trajectory planning of the manipulator using traditional cubic spline interpolation, an improved cubic spline trajectory planning method with continuous third derivative is proposed. This interpolation method adds a correction factor to each cubic interval of cubic spline interpolation. The correction factor in the first segmented interval is a fifth-order function, which solves the problem that the joint′s initial acceleration is not zero. The remaining segmented intervals are all sixth-order functions, which solved the problem of discontinuous third derivatives and non-zero acceleration of the end position. This interpolation method is used to trajectory planning simulation of the six-joint axis manipulator with twenty nodes. The results show that the improved spline interpolation method obtains a continuous third derivative trajectory in the trajectory planning of the manipulator, which effectively reduces the residual vibration of the joint axis.
-
Key words:
- manipulator /
- third derivative continuous /
- acceleration /
- trajectory planning /
- simulation
-
表 1 任意两关节的20个节点数据表
关节 节点 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 x/(°) -30 -20 50 30 70 110 150 -60 -70 80 90 20 -50 -100 -30 -60 -90 -10 50 70 y/(°) -60 -100 -170 -60 -25 65 35 2 20 -60 -130 -80 -30 -15 -90 -40 20 100 120 160 -
[1] 杜严锋, 王聪. 柔性机械臂残余振动控制[J]. 振动与冲击, 2019, 38(7): 165-171 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201907025.htmDU Y F, WANG C. Residual vibration control for a flexible manipulator[J]. Journal of Vibration and Shock, 2019, 38(7): 165-171 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201907025.htm [2] FANG Y, HU J, SHAO Q Q, et al. Fifth order trajectory planning for reducing residual vibration[C]//Proceedings of 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM). Toyonaka, Japan: IEEE, 2019: 999-1004 [3] 李光, 刘领化. 基于轨迹规划方法的单连杆柔性臂振动抑制[J]. 机械科学与技术, 2012, 31(8): 1369-1372, 1376 https://journals.nwpu.edu.cn/jxkxyjs/article/id/5620LI G, LIU L H. Vibration suppression of a one-link flexible arm using trajectory planning method[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(8): 1369-1372, 1376 (in Chinese) https://journals.nwpu.edu.cn/jxkxyjs/article/id/5620 [4] 陆佳皓, 平雪良. 一种机械臂最优时间-冲击轨迹优化算法[J]. 机械科学与技术, 2019, 38(10): 1548-1554 doi: 10.13433/j.cnki.1003-8728.20190012LU J H, PING X L. Time-jerk-optimal trajectory planning algorithm for manipulators[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(10): 1548-1554 (in Chinese) doi: 10.13433/j.cnki.1003-8728.20190012 [5] HUANG Q H, HUANG Y P, HU W, et al. Bezier interpolation for 3-D freehand ultrasound[J]. IEEE Transactions on Human-Machine Systems, 2015, 45(3): 385-392 doi: 10.1109/THMS.2014.2374551 [6] 何雪明, 施国江, 武美萍, 等. B样条在螺杆转子型线反向设计方法中的应用[J]. 机械科学与技术, 2018, 37(1): 43-54 doi: 10.3969/j.issn.2095-509X.2018.01.009HE X M, SHI G J, WU M P, et al. Application of B-spline in reverse design method of screw rotor profiles[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(1): 43-54 (in Chinese) doi: 10.3969/j.issn.2095-509X.2018.01.009 [7] GHASEMI M. On using cubic spline for the solution of problems in calculus of variations[J]. Numerical Algorithms, 2016, 73(3): 685-710 doi: 10.1007/s11075-016-0113-z [8] CHOWDHURY M F I, JEANNEROD C P, NEIGER V, et al. Faster algorithms for multivariate interpolation with multiplicities and simultaneous polynomial approximations[J]. IEEE Transactions on Information Theory, 2015, 61(5): 2370-2387 doi: 10.1109/TIT.2015.2416068 [9] 温冠华, 滕召胜, 林海军, 等. 基于拉格朗日抛物线插值的毛细管粘度仪液位检测方法[J]. 计量学报, 2018, 39(1): 47-51 doi: 10.3969/j.issn.1000-1158.2018.01.11WEN G H, TENG Z S, LIN H J, et al. A liquid-level detection method for capillary viscometer based on Lagrange parabolic interpolation[J]. Acta Metrologica Sinica, 2018, 39(1): 47-51 (in Chinese) doi: 10.3969/j.issn.1000-1158.2018.01.11 [10] LIAGA R J. Real-time estimation of zero crossings of sampled signals for timing using cubic spline interpolation[J]. IEEE Transactions on Nuclear Science, 2017, 64(8): 2414-2422 http://www.researchgate.net/profile/Ramon_Aliaga2/publication/317988554_Real-time_estimation_of_zero_crossings_of_sampled_signals_for_timing_using_cubic_spline_interpolation/links/59e6437faca2721fc227a374/Real-time-estimation-of-zero-crossings-of-sampled-signals-for-timing-using-cubic-spline-interpolation.pdf?origin=publication_detail [11] 李军伟, 程咏梅, 陈克喆, 等. 基于AIWCPSO算法的三次样条气动参数插值方法[J]. 控制与决策, 2014, 29(1): 129-134 https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201401021.htmLI J W, CHENG Y M, CHEN K Z, et al. Cubic spline interpolation method of aerodynamic parameters based on AIWCPSO algorithm[J]. Control and Decision, 2014, 29(1): 129-134 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201401021.htm [12] 吴宪祥, 郭宝龙, 王娟. 基于粒子群三次样条优化的移动机器人路径规划算法[J]. 机器人, 2009, 31(6): 556-560 doi: 10.3321/j.issn:1002-0446.2009.06.013WU X X, GUO B L, WANG J. Mobile robot path planning algorithm based on particle swarm optimization of cubic splines[J]. Robot, 2009, 31(6): 556-560 (in Chinese) doi: 10.3321/j.issn:1002-0446.2009.06.013 [13] LI J C, SONG L Z, LIU C Z. The cubic trigonometric automatic interpolation spline[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(6): 1136-1141 doi: 10.1109/JAS.2017.7510442 [14] BAI Y, WANG D L. On the comparison of Trilinear, cubic spline, and fuzzy interpolation methods in the high-accuracy measurements[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(5): 1016-1022 doi: 10.1109/TFUZZ.2010.2064170 [15] 张小江, 高秀华. 三次样条插值在机器人轨迹规划应用中的改进研究[J]. 机械设计与制造, 2008(9): 170-171 doi: 10.3969/j.issn.1001-3997.2008.09.071ZHANG X J, GAO X H. The research on the cubic splines in robot's trajectory planning[J]. Machinery Design & Manufacture, 2008(9): 170-171 (in Chinese) doi: 10.3969/j.issn.1001-3997.2008.09.071 [16] CHEN D C, QIAO T J, TAN H Z, et al. Solving the problem of Runge phenomenon by pseudoinverse cubic spline[C]// Proceedings of 2014 IEEE 17th International Conference on Computational Science and Engineering. Chengdu, China: IEEE, 2014: 1226-1231 -







 下载:
下载: