一种密度约束的拓扑优化方法

闫晓磊; 谢露; 陈佳文; 花海燕; 黄晓东

doi:10.13433/j.cnki.1003-8728.20200077

一种密度约束的拓扑优化方法

doi: 10.13433/j.cnki.1003-8728.20200077

1.
福建省汽车电子与电驱动重点实验室(福建工程学院), 福州 350118
2.
澳大利亚斯威本科技大学科学、工程与技术学院, 澳大利亚维多利亚 3122

基金项目:

国家自然科学基金项目 51905100

福建省高校杰出青年科研人才培育计划 GY-Z160148

福建省客车及特种车辆研发协同创新中心项目 2016BJC012

闽江学者科研基金项目 GY-Z17015

详细信息

作者简介:
闫晓磊(1981-), 教授, 博士, 研究方向为结构创新设计与轻量化, yanxiaolei@fjut.edu.cn

中图分类号: TH12
计量
- 文章访问数: 228
- HTML全文浏览量: 88
- PDF下载量: 44
- 被引次数: 0
出版历程
- 收稿日期: 2019-11-06
- 刊出日期: 2021-03-01

A Density-constrained Topological Optimization Method

1.
Fujian Key Laboratory of Automotive Electronics and Electric Drive (Fujian University of Technology), Fuzhou 350118, China
2.
Faculty of Science, Engineering and Technology, Swinburne University of Technology, Victoria 3122, Australia

摘要

摘要: 拓扑优化方法是改善结构性能、实现结构创新设计的有效手段。本文采用浮动映射技术，提出了一种密度约束的拓扑优化(Density-constrained topology optimization, DCTO)方法。该方法不同于SIMP方法，采用线性无惩罚材料插值模型，通过准则优化，首先找到结构的最优“厚度”(材料相对密度)分布，然后通过浮动映射函数不断对材料相对密度施加约束，使其逐渐趋于0/1分布。所提出拓扑优化方法的材料相对密度直接代表了材料在结构中的“厚度”分布，其求解原理与SIMP方法有着本质区别。数值算例表明，该方法得到的拓扑结构边界更清晰、光滑，且可避免材料插值模型选取问题。
- 拓扑优化 /
- Heaviside映射 /
- 材料插值模型 /
- 变密度
Abstract: Topological optimization is an effective means to improve structural performance and achieve totally novel designs. With the Heaviside projection function, this article presents a topological optimization method based on constraining the density design variables. The method adopts a linear material interpolation model without penalization, which is quite different from the solid isotropic material with penalization (SIMP) method. Its basic idea is, firstly, to find the optimal structural ″thickness″ (material density) distribution with the optimality criterion method. Secondly, sequential constraints are applied to the material density distribution through a floating projection function to push it towards a 0/1 distribution step by step. In this topological optimization method, the material density directly represents the material ″thickness″ distribution in the structure. Therefore the solutions of the proposed topological optimization method are fundamentally different from the SIMP method. Numerical examples demonstrate that the proposed method can obtain clearer and smoother structural topologies and avoid the difficulties in selecting artificial material interpolation schemes.
- topological optimization /
- Heaviside projection /
- material interpolation model /
- variable density

HTML全文

图 1 DCTO方法流程

下载: 全尺寸图片幻灯片

图 2 悬臂梁设计域

下载: 全尺寸图片幻灯片

图 3 悬臂梁目标柔度C的收敛曲线

下载: 全尺寸图片幻灯片

图 4 Heaviside浮动映射函数β值的迭代图

下载: 全尺寸图片幻灯片

图 5 DCTO法优化的悬臂梁拓扑(V_f^*=0.4)

下载: 全尺寸图片幻灯片

图 6 不同方法的目标柔度C的收敛曲线

下载: 全尺寸图片幻灯片

图 7 形心受集中质量的两端固支梁设计域

下载: 全尺寸图片幻灯片

图 8 不同方法目标固有频率ω的收敛曲线

下载: 全尺寸图片幻灯片

图 9 三维支座设计域

下载: 全尺寸图片幻灯片

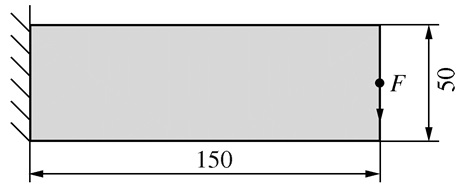
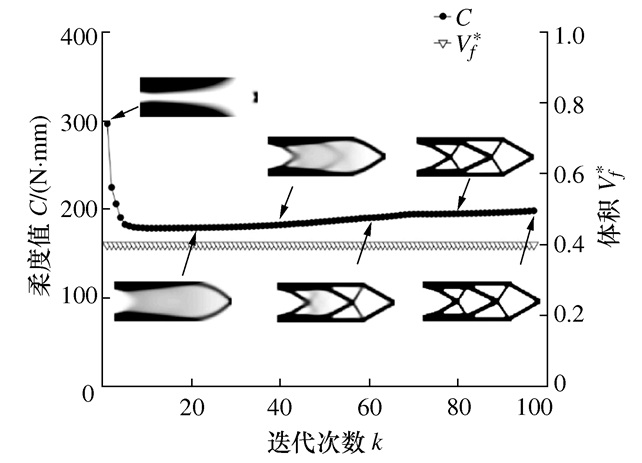
表 1 不同方法的悬臂梁柔度优化结果对比(V_f^*=0.4)

优化方法及目标函数	优化拓扑图(深色)及其相对密度等高线图(浅色)
SIMP (C=230.03 N·mm)
BESO (C=202.21 N·mm)
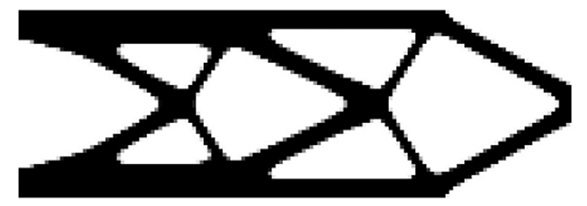
文本DCTO (C=199.12 N·mm)

下载: 导出CSV

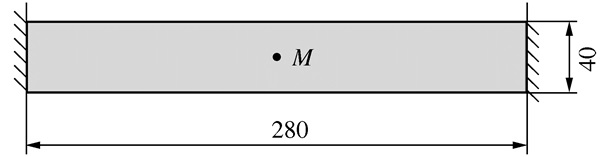
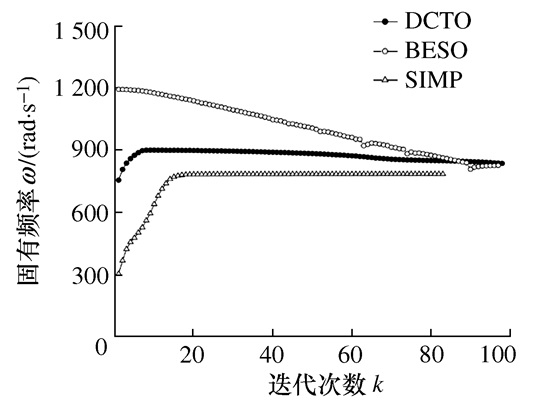
表 2 不同方法的固支梁固有频率优化结果对比

优化方法及目标函数	优化拓扑图(深色)及其相对密度等高线图(浅色)
SIMP ω=783.3 rad/s
BESO ω=825.1 rad/s
文本DCTO ω=834.3 rad/s

下载: 导出CSV

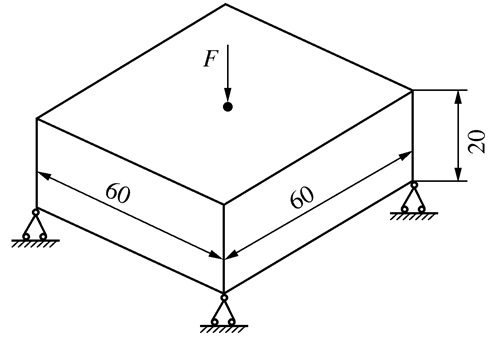
表 3 DCTO方法的三维支座拓扑优化结果

体积约束及目标柔度C	优化拓扑图(深色)及相对密度等高线图(浅色)
V_f^*=0.2 C=196.16 N·mm
V_f^*=0.1 C=250.50 N·mm

下载: 导出CSV

参考文献(21)

[1]	BENDSØE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224 doi: 10.1016/0045-7825(88)90086-2
[2]	WANG M Y, WANG X M, GUO D M. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1-2): 227-246 doi: 10.1016/S0045-7825(02)00559-5
[3]	BENDSØE M P, SIGMUND O. Topology optimization: theory, method and applications[M]. Berlin: Springer Verlag, 2003
[4]	HUANG X, XIE Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J]. Computational Mechanics, 2009, 43(3): 393-401 doi: 10.1007/s00466-008-0312-0
[5]	LIU C, ZHU Y C, SUN Z, et al. An efficient Moving Morphable Component (MMC)-based approach for multi-resolution topology optimization[J]. Structural and Multidisciplinary Optimization, 2018, 58(6): 2455-2479 doi: 10.1007/s00158-018-2114-0
[6]	CUI M T, LUO C C, LI G, et al. The parameterized level set method for structural topology optimization with shape sensitivity constraint factor[J]. Engineering with Computers, 2019: 1-18
[7]	庄春刚, 熊振华, 丁汉. 基于水平集方法和von Mises应力的结构拓扑优化[J]. 中国机械工程, 2006, 17(15): 1589-1595 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX200615012.htm ZHUANG C G, XIONG Z H, DING H. Structural topology optimization based on level set method and von Mises Stress[J]. China Mechanical Engineering, 2006, 17(15): 1589-1595 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX200615012.htm
[8]	SIGMUND O, MAUTE K. Topology optimization approaches: a comparative review[J]. Structural and Multidisciplinary Optimization, 2013, 48(6): 1031-1055 doi: 10.1007/s00158-013-0978-6
[9]	BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9-10): 635-654 doi: 10.1007/s004190050248
[10]	邓扬晨, 张卫红, 邱克鹏, 等. 力学建模在变密度法中密度与刚度关系中的应用[J]. 机械科学与技术, 2003, 22(S1): 95-98 https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX2003S2033.htm DENG Y C, ZHANG W H, QIU K P, et al. An application to mechanical modeling to the relation between density variable and stiffness in variable density approach[J]. Mechanical Science and Technology for Aerospace Engineering, 2003, 22(S1): 95-98 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX2003S2033.htm
[11]	WANG F W, LAZAROV B S, SIGMUND O. On projection methods, convergence and robust formulations in topology optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 767-784 doi: 10.1007/s00158-010-0602-y
[12]	XIA L, XIA Q, HUANG X D, et al. Bi-directional evolutionary structural optimization on advanced structures and materials: a comprehensive review[J]. Archives of Computational Methods in Engineering, 2018, 25(2): 437-478 doi: 10.1007/s11831-016-9203-2
[13]	郭中泽, 陈裕泽, 张卫红, 等. 基于单元材料属性更改的结构渐进拓扑优化方[J]. 机械科学与技术, 2006, 25(8): 928-931 https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX200608010.htm GUO Z Z, CHEN Y Z, ZHANG W H, et al. An evolutionary structural optimization (ESO) method based on element′s properties changing method[J]. Mechanical Science and Technology for Aerospace Engineering, 2006, 25(8): 928-931 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX200608010.htm
[14]	YU M H, RUAN S L, WANG X Y, et al. Topology optimization of thermal-fluid problem using the MMC-based approach[J]. Structural and Multidisciplinary Optimization, 2019, 60(1): 151-165 doi: 10.1007/s00158-019-02206-w
[15]	ZHANG W S, LI D, YUAN J, et al. A new three-dimensional topology optimization method based on moving morphable components (MMCs)[J]. Computational Mechanics, 2017, 59(4): 647-665 doi: 10.1007/s00466-016-1365-0
[16]	SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization, 2001, 21(2): 120-127 doi: 10.1007/s001580050176
[17]	陈成, 荣见华, 易珏虹, 等. 含有Heaviside密度映射的构型平稳变化的柔性机构拓扑优化设计[J]. 机械科学与技术, 2019, 39(1): 129-136 https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX202001022.htm CHEN C, RONG J H, YI J H, et al. Optimizing topological design of compliant mechanism with steady change in its configuration with Heaviside density projection[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 39(1): 129-136 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX202001022.htm
[18]	XU S L, CAI Y W, CHENG G D. Volume preserving nonlinear density filter based on heaviside functions[J]. Structural and Multidisciplinary Optimization, 2010, 41(4): 495-505 doi: 10.1007/s00158-009-0452-7
[19]	SIGMUND O, PETERSSON J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural Optimization, 1998, 16(1): 68-75 doi: 10.1007/BF01214002
[20]	ANDREASSEN E, CLAUSEN A, SCHEVENELS M, et al. Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 1-16 doi: 10.1007/s00158-010-0594-7
[21]	HUANG X D, XIE Y M. A further review of ESO type methods for topology optimization[J]. Structural and Multidisciplinary Optimization, 2010, 41(5): 671-683 doi: 10.1007/s00158-010-0487-9