Study on Stress Relaxation and Life Prediction of Canted Coil Spring
-
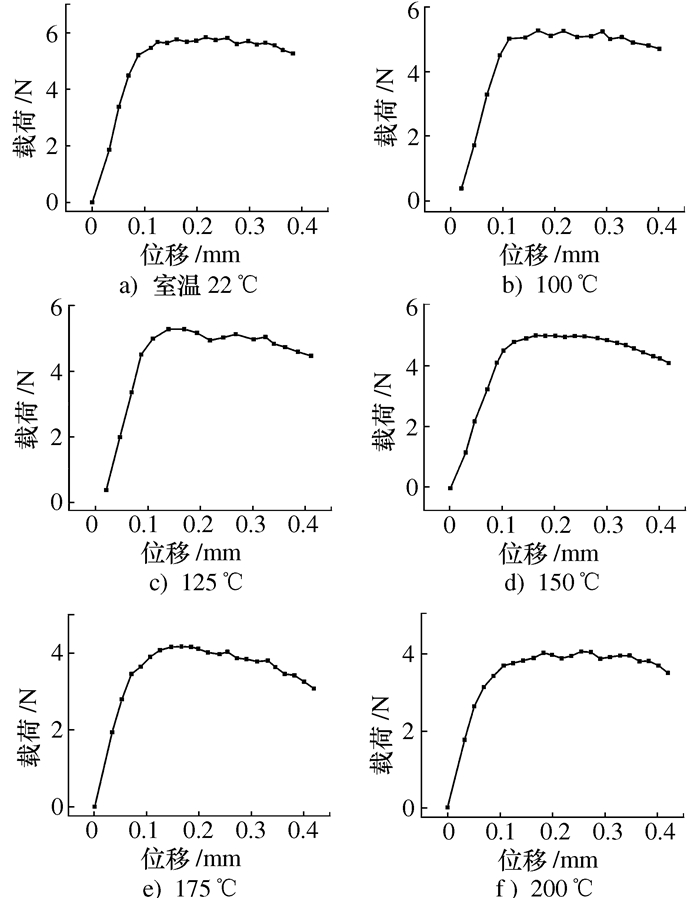
摘要: 为了预防长时间的高温高压环境所产生的应力松弛现象,本文将传统应力松弛理论与Arrhenius理论相结合建立用于斜圈弹簧的应力松弛模型。通过在不同载荷和不同温度下的应力松弛加速试验,探究弹簧应力松弛模型参数的变化规律,实现预测实际工作环境下斜圈弹簧的松弛特性以及服役寿命。通过workbench对单圈弹簧进行有限元仿真分析,不仅可以得出弹簧的载荷松弛量和内部等效应力松弛率,还可以看出在弹簧发生应力松弛后的位移变化以及蠕变量的大小。通过改变弹簧的结构参数,运用workbench分析不同结构参数下单圈弹簧的应力松弛率,探究结构参数与应力松弛率之间的关系,为提高弹簧寿命给出理论依据。Abstract: In order to prevent the stress relaxation caused by the high temperature and high pressure environment in long time, the traditional stress relaxation theory and Arrhenius theory are combined to establish the stress relaxation of the canted coil spring. Through the stress relaxation acceleration test under different loads and temperatures, the variation law of the spring stress relaxation model parameters is explored to predict the relaxation characteristics and service life of the canted coil ring spring under the actual servicing environment. Through the finite element simulation analysis of the single-turn spring by the workbench, the load relaxation amount and the internal equivalent stress relaxation rate of the spring can be not only obtained, the displacement change and the creep variable after the stress relaxation of the spring can be but also seen. By changing the structural parameters of the spring, the workbench is used to analyze the stress relaxation rate of the single-turn spring under different structural parameters, and the relationship between the structural parameters and the stress relaxation rate is explored, which provides a theoretical basis for improving the spring life.
-
Key words:
- canted coil spring /
- stress relaxation /
- arrhenius theory /
- service life /
- creep /
- finite element analysis
-
表 1 铍青铜C17500热物理性能和力学特性
密度/(kg·m-3) 弹性模量/GPa 热膨胀系数/℃-1 热传导系数/W·(m·℃)-1 屈服强度/MPa 延伸率/% 8 830 138 1.76×10-6 208 951 14 表 2 200 ℃恒温不同载荷下的松弛模型参数表
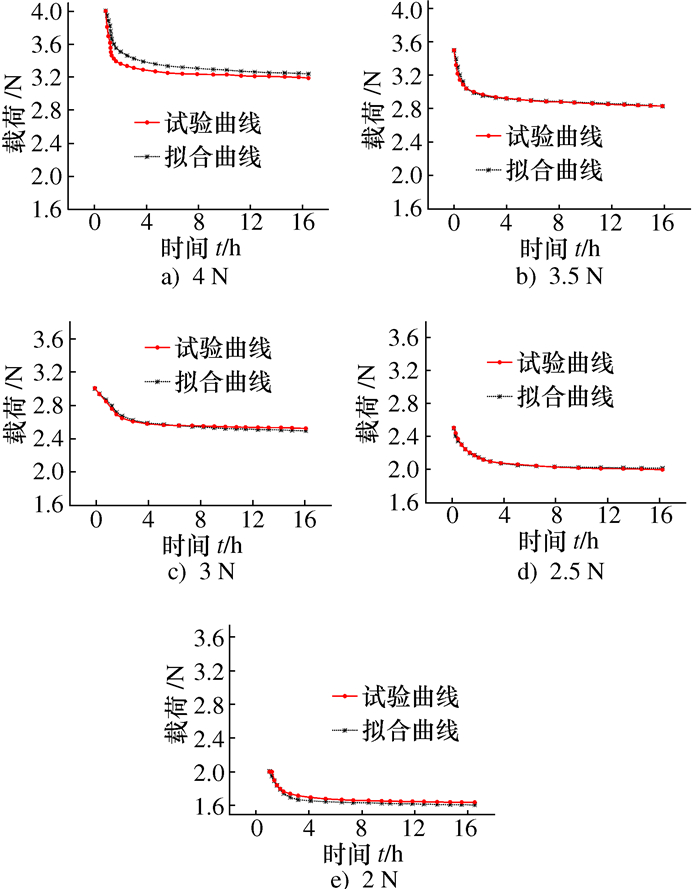
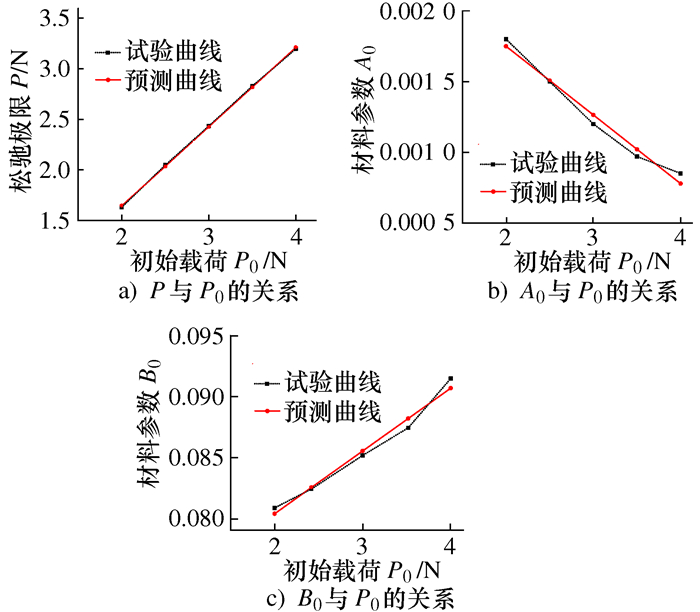
试验载荷P0/N 松弛极限P/N 材料参数A0 材料参数B0 温度参数C1 温度参数C2 4.0 3.198 8.5×10-4 0.091 5 -30.96 -42.28 3.5 2.83 9.5×10-4 0.087 5 -30.96 -42.28 3.0 2.433 1×10-3 0.085 2 -30.96 -42.28 2.5 2.047 1.5×10-3 0.082 5 -30.96 -42.28 2.0 1.63 1.8×10-3 0.080 9 -30.96 -42.28 表 3 恒温不同载荷下松弛模型参数预测表达式
曲线 拟合表达式 相关系数 P-P0 y=0.784x+0.075 6 0.999 A0-P0 y=-4.86×10-4x+2.72×10-3 0.977 B0-P0 y=0.005 14x+0.070 2 0.978 表 4 4 N恒载不同温度下的模型参数表
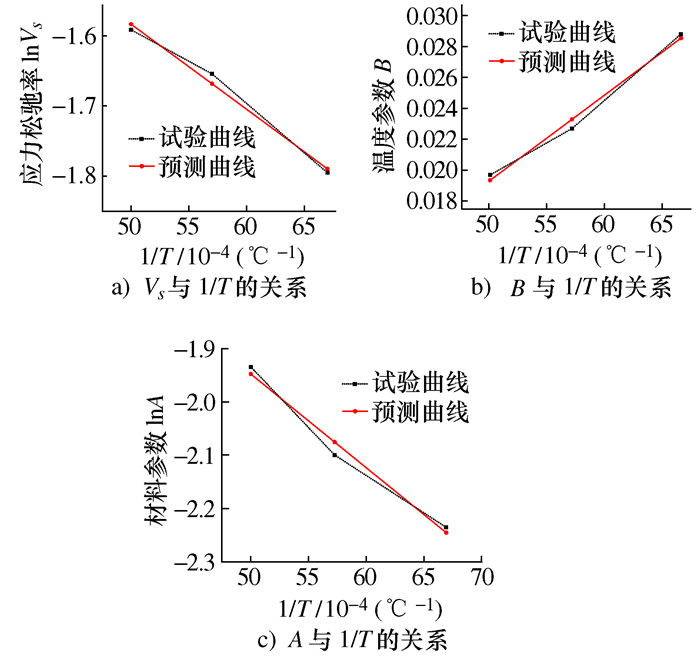
试验温度T/℃ 松弛极限P/N 材料参数A0 材料参数B0 温度参数C1 温度参数C2 200 3.198 8.5×10-4 0.091 5 -30.96 -42.28 175 3.24 8.5×10-4 0.091 5 -32.52 -47.54 150 3.34 8.5×10-4 0.091 5 -35.01 -61.47 125 3.52 8.5×10-4 0.091 5 -37.38 -89.32 100 3.62 8.5×10-4 0.091 5 -40.52 -94.54 表 5 恒载不同温度下松弛模型参数预测表达式
曲线 拟合表达式 相关系数 lnΔ P/P0-1/T y=-160.7x-0.764 9 0.987 C1-1/T y=-192 1x-21.62 0.99 C2-1/T y=-1.14×104x+16.07 0.977 表 6 斜圈弹簧结构参数变化设计表
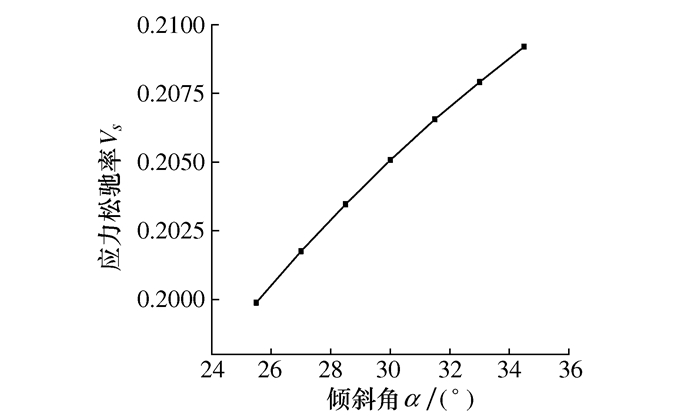
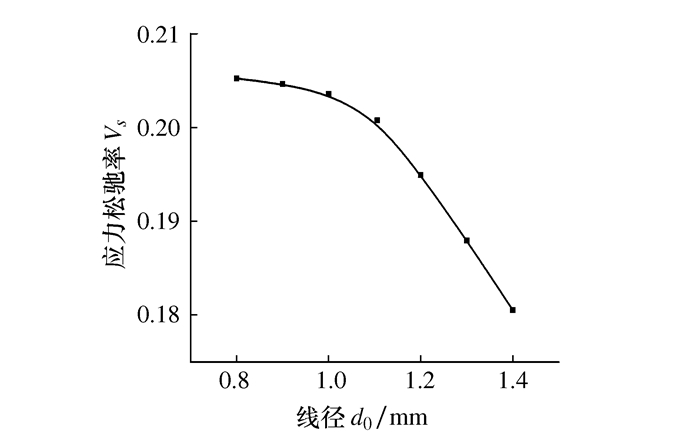
变量 原始值 最小值 最大值 增量 宽度d /mm 8.2 7.2 10.2 0.5 倾斜角α /(°) 28.5 25 34 1.5 截距P /mm 2.05 1.95 2.55 0.1 线径d0/mm 1.0 0.8 1.4 0.1 -
[1] Balsells P J. Use of an axial canted coil spring as an electrical contact to minimize resistivity variations under dynamic loads: US, 7274964[P]. 2007-09-25 [2] 王建平, 李健, 赵腾, 等.斜圈弹簧刚度测量方法研究及实验分析[J].机械科学与技术, 2015, 34(10):1584-1588 doi: 10.13433/j.cnki.1003-8728.2015.1020Wang J P, Li J, Zhao T, et al. Study on stiffness measuring method and experimental analysis for canted coil spring[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(10):1584-1588(in Chinese) doi: 10.13433/j.cnki.1003-8728.2015.1020 [3] 张旭龙, 陈毅, 潘连玉阳, 等.斜圈弹簧的应用研究[J].河南科技, 2013, (4):128 http://d.old.wanfangdata.com.cn/Periodical/hnkj201304113Zhang X L, Chen Y, Pan L Y Y, et al. Application research of inclined coil spring[J]. Journal of Henan Science and Technology, 2013, (4):128(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hnkj201304113 [4] Seshadri R. The effect of multiaxiality and follow-up on creep damage[J]. Journal of Pressure Vessel Technology, 1990, 112(4):378-385 doi: 10.1115/1.2929892 [5] Seshadri R. Multiaxial relaxation and creep damage assessments-a comparison of ASME N-47 and GLOSS time-scaling methods[J]. Journal of Pressure Vessel Technology, 1993, 115(1):32-37 doi: 10.1115/1.2929492 [6] Severud L K. Creep-fatigue assessment methods using elastic analysis results and adjustments[J]. Journal of Pressure Vessel Technology, 1991, 113(1):34-40 doi: 10.1115/1.2928725 [7] 王爱民, 王勖成.高温结构应力松弛和蠕变损伤分析的实用方法[J].机械强度, 2001, 23(1):4-7 http://d.old.wanfangdata.com.cn/Periodical/jxqd200101002Wang A M, Wang X C. Practical method for stress relaxation and creep damage in high-temperature structures[J]. Journal of Mechanical Strength, 2001, 23(1):4-7(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxqd200101002 [8] 常新龙, 刘兵吉, 汪亮.螺旋弹簧应力松弛实验研究[J].推进技术, 1999, 20(1):99-102 http://d.old.wanfangdata.com.cn/Periodical/tjjs199901024Chang X L, Liu B J, Wang L. Experimental study on stress relaxation of helical spring[J]. Journal of Propulsion Technology, 1999, 20(1):99-102(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/tjjs199901024 [9] Zhang C, Li X Q, Li D S, et al. Modelization and comparison of Norton-Hoff and Arrhenius constitutive laws to predict hot tensile behavior of Ti-6Al-4V alloy[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S2):S457-S464 [10] 张力文, 钟玉平.金属高温蠕变理论研究进展及应用[J].材料导报, 2015, (S1):409-416 http://www.cnki.com.cn/Article/CJFDTotal-CLDB2015S1106.htmZhang L W, Zhong Y P. Development and application of metal creep theory method under high temperature[J]. Materials Review, 2015, (S1):409-416(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-CLDB2015S1106.htm [11] 苏德达, 朱知寿, 王欣华.奥氏体不锈压缩螺旋弹簧抗应力松弛性能研究[J].金属制品, 1997, 23(2):12-18 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700313569Su D D, Zhu Z S, Wang X H. Research on anti-stress relaxational ability of helical compression springs made of austenitic stainless steel wires[J]. Steel Wire Products, 1997, 23(2):12-18(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700313569 [12] 赵伯华.松弛与蠕变力学特性转换关系的研究[J].实验力学, 1995, 10(2):140-144 http://www.cnki.com.cn/Article/CJFDTotal-SYLX502.006.htmZhao B H. Conversion relations between relaxation and creep[J]. Journal of Experimental Mechanics, 1995, 10(2):140-144(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-SYLX502.006.htm [13] 王敏中.高等弹性力学[M].北京:北京大学出版社, 2002Wang M Z. Higher elasticity[M]. Beijing:Peking University Press, 2002(in Chinese) [14] Ghosh R N. Creep life predictions of engineering components:problems & prospects[J]. Procedia Engineering, 2013, 55:599-606 doi: 10.1016/j.proeng.2013.03.301 [15] 张维维.电站高温螺栓松弛力学行为的研究[D].北京: 华北电力大学, 2015 https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&filename=1015643935.nhZhang W W. Research on stress relaxation behaviour of high temperature bolts in power plants[D]. Beijing: North China Electric Power University, 2015(in Chinese) https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&filename=1015643935.nh -








 下载:
下载: