Dynamic Control Method of Parallel Manipulator with two Degrees of Freedom
-
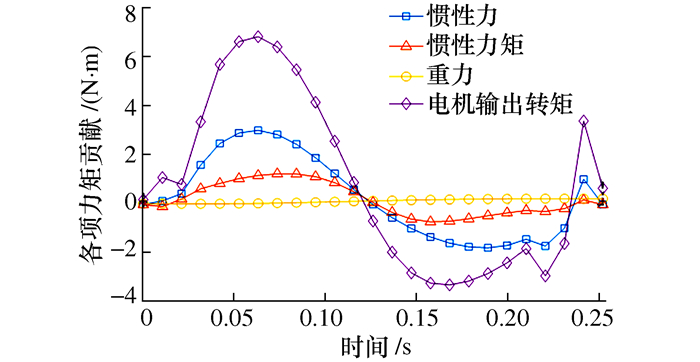
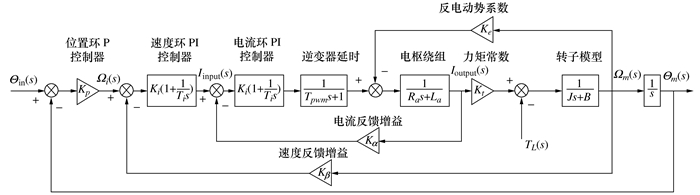
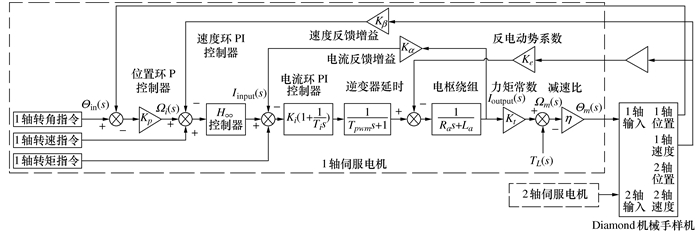
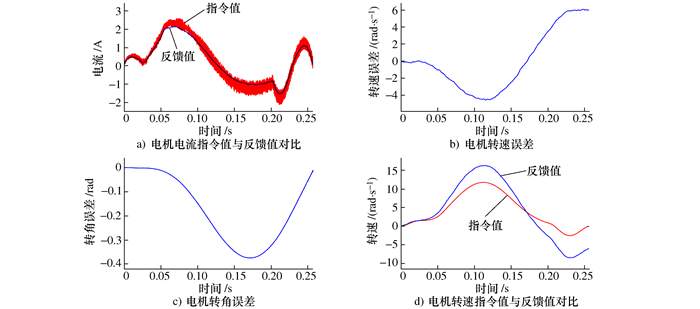
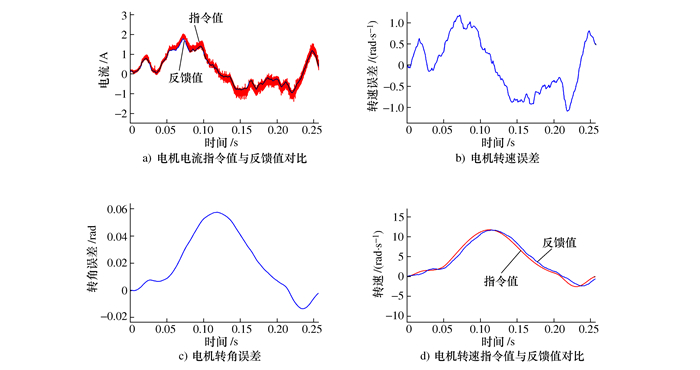
摘要: 本文针对一种二自由度并联机械手高速运动状态下的动力学控制方法展开研究。通过对并联机械手简化刚体动力学模型的建模误差进行溯源分析,提出了一种基于双系数补偿分配策略的建模方法,对机械手的简化刚体动力学模型进行了优化,并基于该简化模型建立了机械手的动力学前馈控制方法。为进一步提高控制过程的鲁棒性,结合H∞控制方法提出了一种H∞+动力学前馈的控制方法。在建立机械手整机机电联合仿真系统的基础上,对所提出的两种控制方法进行了详细的仿真和对比。仿真结果表明,本文提出的控制方法可以减少力矩扰动对伺服电机输出带来的影响,大大减小了机械手末端的定位误差,提高了机械手的控制精度。Abstract: In this paper, the dynamic control method of a 2-DOF parallel manipulator under high-speed motion is studied. By tracing the error of the simplified rigid-body dynamic model for parallel manipulator, a modeling method based on the two-coefficient compensation allocation strategy is proposed, and the simplified rigid-body dynamic model for the manipulator is optimized. Based on the simplified model, a dynamic feedforward control method of the manipulator was established. In order to further improve the robustness of the control process, an H∞+ dynamic feedforward control method is proposed. Based on the establishment of the mechanical and electrical joint simulation system of the manipulator, the two control methods are simulated and compared in detail. The simulation results show that the control method proposed in this paper can reduce the influence of the torque disturbance on the output of servo motor and greatly reduce the positioning error of the end of the manipulator, improving the control accuracy of the manipulator.
-
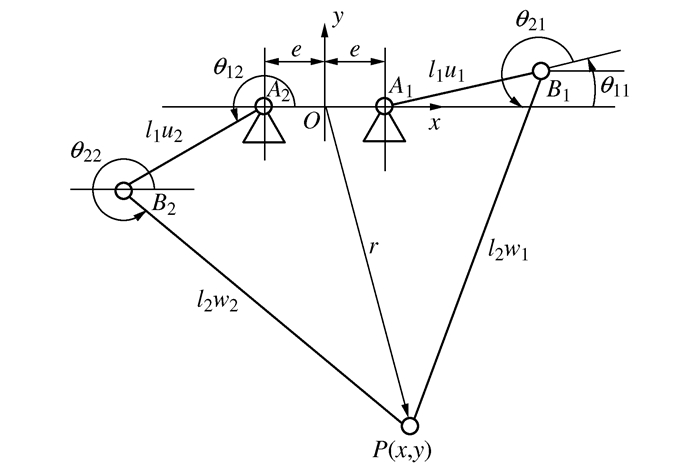
表 1 公式(2)符号释义表
符号 含义 表达式 θ1 主动臂转角 θ1=(θ11 θ12)T θ2 从动臂转角 θ2=(θ21 θ22)T rdi 从动臂质心位置 rdi=(xdi ydi)T τ 主动关节转矩 τ=(τ1 τ2)T 
动平台质心加速度 
m 动平台总质量 m=mplatform+mload IA 主动臂等效到转轴的转动惯量 IA=Iarm+n2Igearbox+mbracketl12 mArA 主动臂等效到转轴的质径积 mArA=marmrarm+mbracketl12 τAg 主动臂对其转轴的重力矩 τAg=mArAg(cosθ11 cosθ12)T fsi 从动臂连杆的惯性力和重力之和 
Mrodi 从动臂连杆的惯性力矩 
注:Iarm为主动臂自身对其转轴的转动惯量; Igearbox为减速器的转动惯量; n为减速器减速比; marmrarm为主动臂关于其转轴的质径积; mrod, Irod分别为从动臂的质量和相对其主轴坐标系的惯性张量; mbracket, mplatform, mload分别为肘架、动平台和负载的质量。 表 2 机械手参数
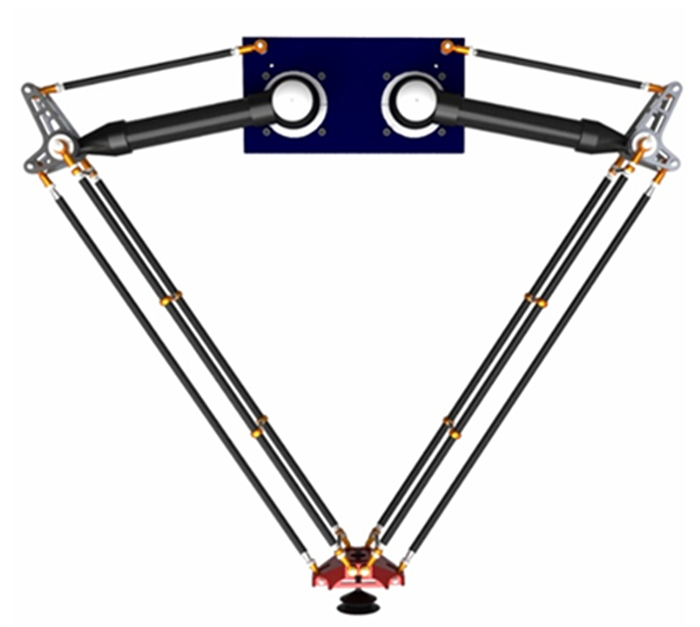
参数 数值 l1 0.35 m l2 0.90 m H 0.70 m e 0.15 m D 1.0 m h 0.25 m mplatform 0.7 kg l1 20:1 Iarm 0.025 2 kg·m2 Irod 0.081 5 kg·m2 Igearbox 0.47×10-4kg·m2 mload 0.2 kg marm 1.285 kg mbracket 0.545 kg mrod 0.789 kg marmrarm 0.146 kg·m 表 3 机械手运动轨迹参数
轨迹高度H 轨迹长度B 最大加速度amax 0.1 m 0.8 m 98.1 m/s2 表 4 驱动电机伺服参数
参数 数值 电流环比例增益Ki/(V·A-1) 17.28 电流环积分时间常数Ti/ms 3.6 逆变器时间常数Tpwm/s 6.25×10-5 电枢绕组电阻R/Ω 1 电枢绕组电感L/mH 3.6 力矩常数Kt/(N·m·A-1) 1.55 等效转动惯量I/(kg·m2) 6×10-4 反电动势系数Ke/(V·s·rad-1) 0.898 减速比η 20 -
[1] Clavel R. Dispositif pour le deplacement et le positionnement d'un element dans l'espace: Switzerland, CH1985005348856[P]. 1985 [2] 黄田, 李曚, 李占贤.仅含转动副的二自由度平动并联机器人机构: 中国, CN1355087A[P].2002-06-26Huang T, Li M, Li Z X. Two-freedom translational parallel robot mechanism containing only rotating sets: China, CN1355087A[P]. 2002-06-26(in Chinese) [3] Huang T, Li Z X, Li M, et al. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations[J]. Journal of Mechanical Design, 2004, 126(3):449-455 doi: 10.1115/1.1711822 [4] Li Y M, Xu Q S. Kinematics and inverse dynamics analysis for a general 3-PRS spatial parallel mechanism[J]. Robotica, 2005, 23(2):219-229 doi: 10.1017/S0263574704000797 [5] Codourey A. Dynamic modelling and mass matrix evaluation of the Delta parallel robot for axes decoupling control[C]//Proceedings of 1996 IEEE/RSJ International Conference on Intelligent Robots and Systems. Osaka: IEEE, 1996: 1211-1218 http://www.researchgate.net/publication/3681152_Dynamic_modelling_and_mass_matrix_evaluation_of_the_DELTA_parallelrobot_for_axes_decoupling_control [6] Codourey A. Dynamic modeling of parallel robots for computed-torque control implementation[J]. The International Journal of Robotics Research, 1998, 17(2):1325-1336 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/027836499801701205 [7] Huang T, Liu S T, Mei J P, et al. Optimal design of a 2-DOF pick-and-place parallel robot using dynamic performance indices and angular constraints[J]. Mechanism and Machine Theory, 2013, 70:246-253 doi: 10.1016/j.mechmachtheory.2013.07.014 [8] Pierrot F, Benoit M, Dauchez P, et al. High speed control of a parallel robot[C]//IEEE International Workshop on Intelligent Robots and Systems, Towards a New Frontier of Applications. Ibaraki, Japan: IEEE, 1990 https://www.researchgate.net/publication/3496177_High_speed_control_of_a_parallel_robot [9] Choi H B, Company O, Pierrot F, et al. Design and control of a novel 4-DOFs parallel robot H4[C]//Proceedings of 2003 IEEE International Conference on Robotics and Automation. Taipei, Taiwan, China: IEEE, 2003: 1185-1191 http://www.researchgate.net/publication/29634313_Design_and_Control_of_a_Novel_4-DOFs_Parallel_Robot_H4 [10] Choi H B, Konno A, Uchiyama M. Design, implementation, and performance evaluation of a 4-DOF parallel robot[J]. Robotica, 2010, 28(1):107-118 doi: 10.1017/S0263574709005621 [11] Huang T, Mei J P, Li Z X, et al. A method for estimating servomotor parameters of a parallel robot for rapid pick-and-place operations[J]. Journal of Mechanical Design, 2005, 127(4):596-601 doi: 10.1115/1.1898343 [12] Zhang L M, Mei J P, Zhao X M, et al. Dimensional synthesis of the delta robot using transmission angle constraints[J]. Robotica, 2011, 30(3):343-349 [13] 梅江平, 贺莹, 臧家炜, 等.Delta并联机械手刚体动力学模型简化方法[J].机械科学与技术, 2018, 37(3):329-336 doi: 10.13433/j.cnki.1003-8728.2018.0301Mei J P, He Y, Zang J W, et al. Simplified method for rigid body dynamic models of delta parallel manipulator[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(3):329-336(in Chinese) doi: 10.13433/j.cnki.1003-8728.2018.0301 [14] Lee S H, Song J B, Choi W C, et al. Position control of a fast parallel robot[C]//Proceedings of 1995 IEEE International Conference on Robotics and Automation. USA: IEEE, 1995, 1: 1178-1183 [15] Zames G, Francis B A. Feedback, minimax sensitivity, and optimal robustness[J]. IEEE Transactions on Automatic Control, 1983, 28(5):585-601 doi: 10.1109/TAC.1983.1103275 [16] 解学书, 钟宜生.H∞控制理论[M].北京:清华大学出版社, 1994Xie X S, Zhong Y S. H-infinity control theory[M]. Beijing:Tsinghua University Press, 1994(in Chinese) [17] 吴旭东, 解学书.H∞鲁棒控制中的加权阵选择[J].清华大学学报, 1997, 37(1):27-30 doi: 10.3321/j.issn:1000-0054.1997.01.001Wu X D, Xie X S. Weighting function matrix selection in H∞ robust control[J]. Journal of Tsinghua University, 1997, 37(1):27-30(in Chinese) doi: 10.3321/j.issn:1000-0054.1997.01.001 [18] Verma M, Jonckheere E A. L∞-compensation with mixed sensitivity as a broadband matching problem[J]. Systems & Control Letters, 1984, 4(3):125-129 http://www.researchgate.net/publication/222752198_L-compensation_with_mixed_sensitivity_as_a_broadband_matching_problem -







 下载:
下载: