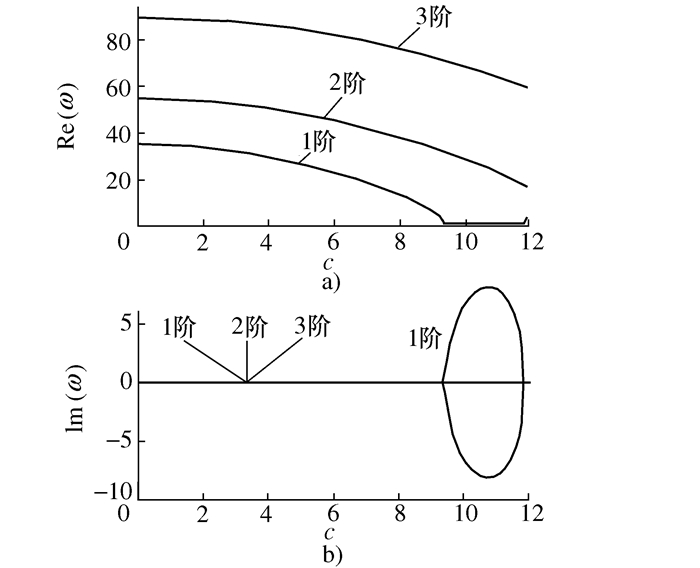
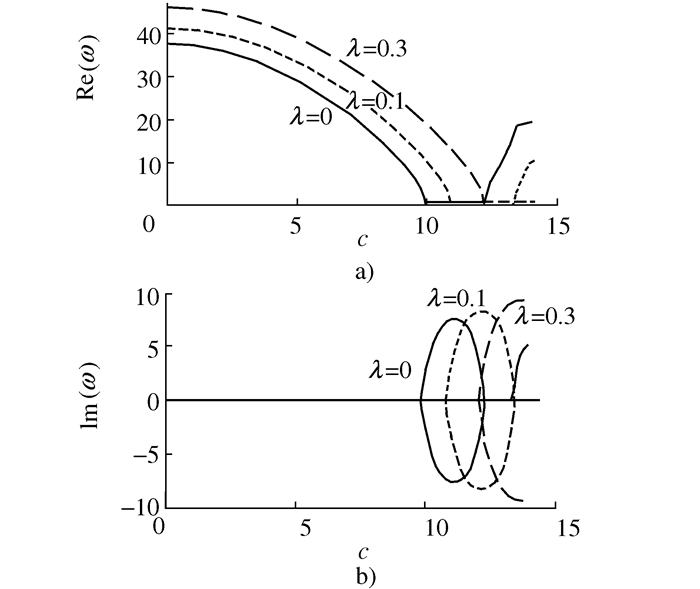
|
[1]
|
Shi D Y, Liu T, Wang Q S, et al. Vibration analysis of arbitrary straight-sided quadrilateral plates using a simple first-order shear deformation theory[J]. Results in Physics, 2018, 11:201-211 doi: 10.1016/j.rinp.2018.09.001
|
|
[2]
|
Muhannad A W, Maher A B. A suggested analytical investigation of heat generation inducing into vibration beam subjected to harmonic loading[J]. International Journal of Energy and Environment, 2018, 9(5):499-514
|
|
[3]
|
吴晓, 黄翀.功能梯度材料椭圆板的非线性热振动及屈曲[J].动力学与控制学报, 2013, 11(2):165-171 http://d.old.wanfangdata.com.cn/Periodical/dlxykzxb201302014Wu X, Huang C. Nonlinear thermal vibration and buckling of functionally graded elliptical plate[J]. Journal of Dynamics and Control, 2013, 11(2):165-171(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/dlxykzxb201302014
|
|
[4]
|
Zhou F X, Li S R, Lai Y M. Three-dimensional analysis for transient coupled thermoelastic response of a functionally graded rectangular plate[J]. Journal of Sound and Vibration, 2011, 330(16):3990-4001 doi: 10.1016/j.jsv.2011.03.015
|
|
[5]
|
Nayak A K, Satapathy A K. Stochastic damped free vibration analysis of composite sandwich plates[J]. Procedia Engineering, 2016, 144:1315-1324 doi: 10.1016/j.proeng.2016.05.130
|
|
[6]
|
贺旭东, 吴松, 张步云, 等.热应力对机翼结构固有频率的影响分析[J].振动、测试与诊断, 2015, 35(6):1134-1139 http://d.old.wanfangdata.com.cn/Periodical/zdcsyzd201506023He X D, Wu S, Zhang B Y, et al. Influence of thermal stress on vibration frequencies of a wing structure[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(6):1134-1139(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/zdcsyzd201506023
|
|
[7]
|
付江松, 徐鉴.四边自由矩形板横向振动的近似解及其实验[J].振动与冲击, 2018, 37(5):92-97, 107 http://d.old.wanfangdata.com.cn/Periodical/zdycj201805014Fu J S, Xu J. An approximate solution to transverse vibration of a rectangular plate with 4 free edges and its experimental verification[J]. Journal of Vibration and Shock, 2018, 37(5):92-97, 107(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/zdycj201805014
|
|
[8]
|
武吉梅, 景涛, 王砚, 等.计及弯曲刚度的印刷运动薄膜横向振动控制研究[J].应用数学和力学, 2015, 36(7):686-699 http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201507002Wu J M, Jing T, Wang Y, et al. Transverse vibration control of moving printing membranes with bending stiffness[J]. Applied Mathematics and Mechanics, 2015, 36(7):686-699(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yysxhlx201507002
|
|
[9]
|
滕兆春, 衡亚洲, 刘露.非均匀Winkler弹性地基上变厚度矩形板自由振动的DTM求解[J].计算力学学报, 2018, 35(2):216-223 http://d.old.wanfangdata.com.cn/Periodical/jslxxb201802013Teng Z C, Heng Y Z, Liu L. Free vibration analysis for rectangular plates with variable thickness resting on a non-uniform Winkler elastic foundation by DTM[J]. Chinese Journal of Computational Mechanics, 2018, 35(2):216-223(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jslxxb201802013
|
|
[10]
|
高俊, 党发宁, 李海斌, 等.静水荷载作用下矩形薄板力学特性研究及其应用[J].应用力学学报, 2018, 35(5):1029-1036 http://d.old.wanfangdata.com.cn/Periodical/yylxxb201805017Gao J, Dang F N, Li H B, et al. The mechanical properties and application of rectangular thin plates under hydrostatic pressure[J]. Chinese Journal of Applied Mechanics, 2018, 35(5):1029-1036(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/yylxxb201805017
|
|
[11]
|
陈林, 肖伟, 刘见华, 等.基于改进傅里叶级数的矩形板薄板振动特性分析[J].噪声与振动控制, 2018, 38(5):21-26 doi: 10.3969/j.issn.1006-1355.2018.05.004Chen L, Xiao W, Liu J H, et al. Vibration characteristic analysis of rectangular thin plates based on improved fourier series method[J]. Noise and Vibration Control, 2018, 38(5):21-26(in Chinese) doi: 10.3969/j.issn.1006-1355.2018.05.004
|
|
[12]
|
Jeong K H, Jhung M J. Free vibration analysis of partially perforated circular plates[J]. Procedia Engineering, 2017, 199:182-187 doi: 10.1016/j.proeng.2017.09.230
|
|
[13]
|
Li C Y, Wu Y C, Chang C Y, et al. Theoretical analysis based on fundamental functions of thin plate and experimental measurement for vibration characteristics of a plate coupled with liquid[J]. Journal of Sound and Vibration, 2017, 394:545-574 doi: 10.1016/j.jsv.2017.01.023
|
|
[14]
|
李天匀, 张俊, 朱翔, 等.含任意形状内开口的矩形板振动特性分析[J].华中科技大学学报, 2018, 46(11):1-6 http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201811001Li T Y, Zhang J, Zhu X, et al. Vibration characteristics analysis on rectangular plates with arbitrarily-shaped cutout[J]. Journal of Huazhong University of Science and Technology, 2018, 46(11):1-6(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hzlgdxxb201811001
|
|
[15]
|
严宗达, 王洪礼.热应力[M].北京:高等教育出版社, 1993Yan Z D, Wang H L. Thermal stress[M]. Beijing:Higher Education Press, 1993(in Chinese)
|
|
[16]
|
Guo X X, Wang Z M, Wang Y, et al. Analysis of the coupled thermoelastic vibration for axially moving beam[J]. Journal of Sound and Vibration, 2009, 325(3):597-608 doi: 10.1016/j.jsv.2009.03.026
|
|
[17]
|
Gorman D J. Free vibration analysis of rectangular plates[M]. New York:Elsevier, 1982
|







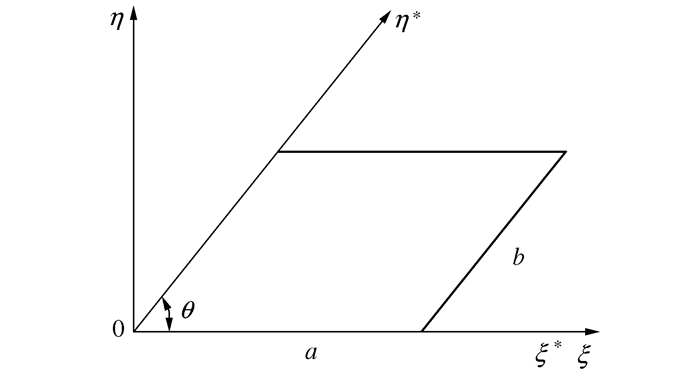
 下载:
下载: